题外话:本体题目出自番剧《NO GAME NO LIFE》且题目背景中
来吧,游戏开始了。
是第一季中男主“空”的口头禅。(强烈推荐观看《NO GAME NO LIFE ZERO》)
回归正题awa
P9355「SiR-1」Checkmate 题解
题目解读:
在 \(n\) 行 \(m\) 列的棋盘中放置多枚棋子,求出其上下左右未被放置棋子的格子数总和的最大值。
题目分析:
由题目可以得到在完全空白的棋盘中,放置在角上能得到 \(2\) 分,放置在棱上能得到 \(3\) 分,放置在中心块(非角、棱区域)能得到 \(4\) 分。在 \(1\) 行或 \(1\) 列时,头、尾部能得 \(1\) 分,中间部分能得 \(2\) 分。
对于 \(2 \times 1\) 的棋盘,放置在左方块(或右方块)上,能得到 \(1\) 分,接下来放置另一方块不会得分(即无贡献)。
拓展到 \(3 \times 1\) 的棋盘,无论先放置在中间的块,得到\(2\)分,还是放置在左右两块各得到 \(1\) 分,合计 \(2\) 分,亦或是从左到右(从右到左)依次排列全部都是 \(2\) 分。
如果我们不考虑已放置的棋子对后面其它棋子产生的影响(即只考虑每一枚棋子单独放置时的得分),将它们的得分相加,我们会发现刚好是上述讨论情况中最高分值的 \(2\) 倍。
另一种更加科学的证明
首先我们先思考放置一枚棋子能带来什么影响(可以先思考一下再接着看)。
设棋盘可以得到的分数为 \(val\),棋盘上的角方块数为 \(T\),棱方块(不包括角方块)数为 \(L\),中心方块(即非角、非棱的方块)数为 \(M\)。
我们在理想的情况下得到的分数是 \(val = 2 \times T + 3 \times L + 4 \times M\),也就是每个块都贡献出了它所能贡献的最大分数,但是毕竟我们应该考虑影响......
于是乎在考虑影响的情况下,我们的每一次放置都将获得一个分值,但是总分数(就是理想情况下的分数)将减去这个分值。因此,我们在考虑影响的情况下的能获得的分值是 \(val = \frac{2 \times M + 3 \times L + 4 \times M}{2}\)。
如图所示:
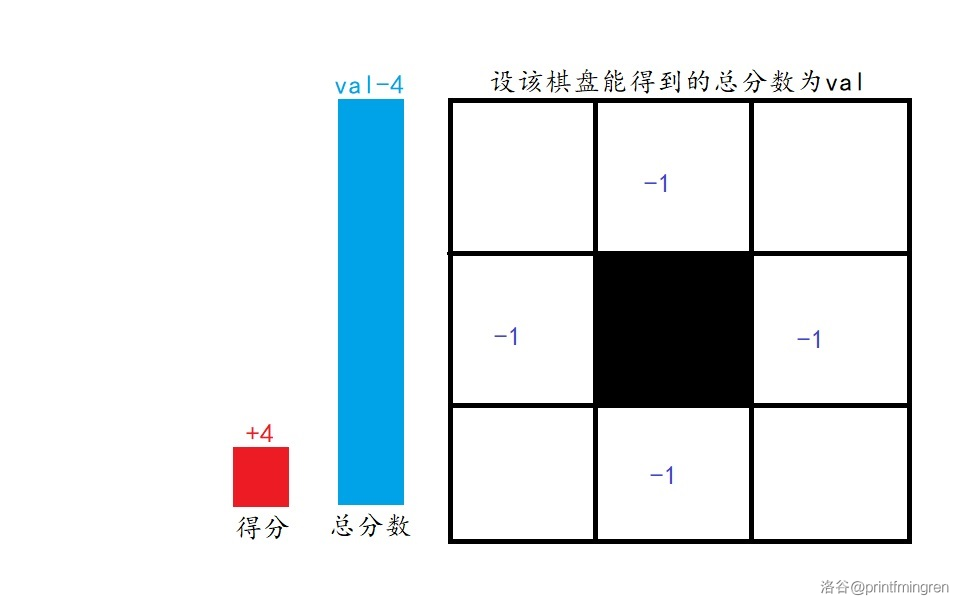
分类讨论情况如下:
1. 当 \(n≥ 2\) 且 \(m ≥ 2\) 时
\(val=\frac{2\times T + 3 \times L + 4 \times M}{2}\)
2. 当 \(n=1\) 或 \(m=1\) 时
\(val=n+m-2\) (每个块能得 \(2\) 分,左右或上下块与中间的块相比各少 \(1\) 分)。
由于 \(n=1\) 或 \(m=1\) ,可得 \(val=n-1\) 或 \(val=m-1\) (合并的时候能用到) 。
从某种意义上来讲就是影响互相抵消。
以上是赛时思路,接下来是合并推导
最终答案为 \(val=\frac{2\times T + 3 \times L + 4 \times M}{2}\)。
根据前文分析得出上方完整式子,接下来对这个式子进行推导:
我们依旧用 \(T,L,M\) 分别代表角、棱、中心块数量,对于每个棋盘,易得
\[T = 4 \]\[L = 2 \times n + 2 \times m - 2 \times T \]\[M = n \times m - T - L \]则总得分为
\[val = \frac{2 \times T + 3 \times L + 4 \times M}{2} \]代入 \(T,L,M\) 可得
\[val = 2 \times n \times m - n - m \]将 \(n = 1\)代入此式可得
\[val = m - 1 \]将 \(m = 1\)代入此式可得
\[val = n - 1 \]当 \(m = n = 1\) 时
\[val = m + n - 2 \]综上,\(val = n + m - 2\) 被 \(val = \frac{2 \times T + 3 \times L + 4 \times M}{2}\) 所包含。
赛时AC代码如下
#include<bits/stdc++.h>
using namespace std;
#define ll long long
int main()
{
ll T;
scanf("%lld",&T);
for(ll i=1;i<=T;++i)
{
ll n,m,a,b,c,sum;
scanf("%lld%lld",&n,&m);
a=4;
b=2*n+2*m-2*a;
c=n*m-a-b;
sum=(a*2+b*3+c*4)/2;
printf("%lld\n",sum);
}
return 0;
}
于是乎我推荐大家试试[THUPC 2023 初赛] 大富翁
感觉两题有相似之处(?)。
我是蒟蒻,加之本题解赶工严重,还请各位大佬指出错误,一同进步。(点个赞再走吧,QAQ)