图是一种数据结构和模型,在计算机中存储图的最简单有效方式就是矩阵。矩阵作为表达图有效工具和手段,也便于运用代数的方法研究图的性质(这才是重点!),例如,我们可以通过矩阵计算结果,判定图的连通性/可达性等问题。
一、邻接矩阵(adjacency matrix)
定义1 设 G = (V,E)是一个图,节点集合$ V = { v_1, v_2, \dots, v_n}$,令 $ A(G) = [a_{ij}]_{n\times n}$,其中:
\[a_{ij} =\begin{cases} 1 \quad &若[v_i, v_j] \in E\\ 0\quad &若[v_i, v_j] \notin E \end{cases} \]则称A(G)为\(G\) 的**邻接矩阵。
【例1】设G1 是有向图、G2 是无向图,分别如下图(a)和(b)所示,写出G1,G2 的邻接矩阵。

**解: **
| \(A(G_1)\) | \(A(G_2)\) |
|---|---|
| $\begin{bmatrix} 1 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0\\ 1 & 1 & 0 & 0 \\ 0 & 0 & 1 & 1 \end{bmatrix} $ | \(\begin{bmatrix} 1 & 1 & 1 & 1 \\ 1 & 0 & 1 & 0\\ 1 & 1 & 0 & 1 \\ 1 & 0 & 1 & 1 \end{bmatrix}\) |
当结点编号次序不同时,同一个图所得的邻接矩阵可能不同,但可以通过有限次的行、列变换而得到相同的邻接矩阵(同构的图?)。
通过图的邻接矩阵运算,可以判断图的一些性质。设G=(V,E) 是有向图, $|V| = n $ ,\(A\)是G 的邻接矩阵。
1.1 \(AA^T\)的元素的意义
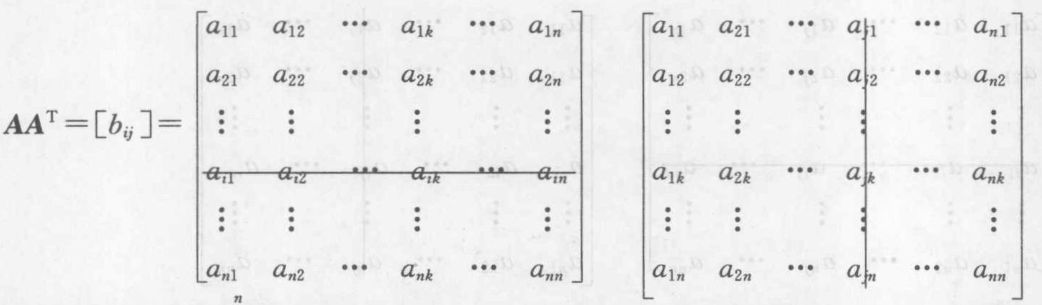
可知,\(b_{ij} = \sum^n_{k = 1} a_{ik} a_{jk}\) ,如上图所示,则在G中恰好有\(b_{ij}\)个结点,从\(v_i\) 和\(v_j\) 均有边引出到这些节点\(v_{k_1}, v_{k_2}, \dots, v_{k_n}\)。特别地,当\(i =j\)时\(b_{ij}\)表示 \(v_i\)的出度。
1.2 \(A^{2} = A\times A\)的元素的意义

若有\(b_{ij} = \sum^n_{k = 1} a_{ik}a_{kj}\),则从\(v_i\) 到\(v_j\) 长度为2 的路有\(b_{ij}\) 条。特别地,当\(i=j\)时\(v_i\) 到自身长度为2 的回路有 $b_{ij} $条。
1.3 有向图的路(path)
【例2】对于有向图G=(V,E),用 G 的邻接矩阵计算从顶点 \(v_3\)到 \(v_1\) 的所有有向通路 。

解:图G 的邻接矩阵为:
由\(A[3][1] = 0\) 知(下标从1开始),从顶点\(v_3\)到 \(v_1\)没有长度为 1 的通路。再计算$A^2 $:
\[\begin{aligned} A^2[3][1] &= A[3][1] \times A[1][1] + A[3][2] \times A[2][1] \\ &+ A[3][3] \times A[3][1] + A[3][4] \times A[4][1] \\ &= 0 \times 0 + 1 \times 0 + 0\times 0 + 1 \times 1 = 1 \end{aligned}\]得到从顶点\(v_3\) 到\(v_1\)的长度为 2 的有向路为\((v_3, v_4, v_1)\)。显然,它也是一条通路。再计算\(A^3\):
\[A^3 =\begin{bmatrix} 1 & 2 & 0 & 1\\ 1 & 2 & 2 & 2 \\ 1 & 3 & 1 & 2 \\ 1 & 2 & 1 & 2 \end{bmatrix} \]由 $ A^3[3][1] = 1 $知,从顶点 \(v_3\) 到\(v_1\) 的长度为3的路有1条。根据计算过程:
\begin{aligned} A^3[3][1] &= A^2[3][1] \times A[1][1] + A^2[3][2] \times A[2][1] \\ &+ A^2[3][3] \times A[3][1] + A^2[3][4] \times A[4][1] \\ &= 1 \times 0 + 1 \times 0 + 1\times 0 + 1 \times 1 = 1 \end{aligned}
得到从顶点\(v_3\)到\(v_1\) 的长度为3的有向路为:从顶点\(v_3\) 到\(v_4\) 的一条长度为2的路接上\((v_4, v_1)\) 。再根据计算过程:
\begin{aligned} A^2[3][4] &= A[3][1] \times A[1][4] + A[3][2] \times A[2][4] \\ &+ A[3][3] \times A[3][4] + A[3][4] \times A[4][4] \\ &= 0 \times 0 + 1 \times 1 + 0\times 1 + 1 \times 0 = 1 \end{aligned}
得到从顶点\(v_3\) 到\(v_4\) 的一条长度为2 的有向路是\((v_3,v_2, v_4)\)。所以,从顶点\(v_3\) 到\(v_1\) 的长度为 3的有向路是 \((v_3, v_2, v_4, v_1)\) 。显然,它也是一条通路。
因为对于4个节点的有向图,当路的长度超过3 时,必定不是通路,所以从顶点\(v_3\) 到\(v_1\) 的通路共有两条:\((v_3, v_4, v_1)\)和$(v_3, v_2, v_4, v_1) $ 。
二、可达矩阵
定义2 设G=(V,E)是一个图,节点集合\(V = \{ v_1, v_2, \dots, v_n\}\),令\(P(G) =[p_{ij}]_{n \times n}\) ,其中:
\[p_{ij} =\begin{cases} 1 \quad &若从 v_i可达 v_j\\ 0 \quad &若从 v_i不可达 v_j \end{cases} \]则称 \(P(G)\) 为G 的可达矩阵。
可达矩阵用于描述一个图中,任一节点到另一节点之间是否存在路。由于在图中「两个结点之间有路」,则「必存在长度小于等于 \(n−1\) 的通路」。另外,一般认为「同一个结点到自身可达」。因此,可用以下公式计算 $$P(G) = [p_{ij} ]_{n\times n} = A^0 \lor A^1 \lor \cdots \lor A^{n - 1}$$
其中,\(A^0\) 是$ n\times n$的单位矩阵, \(∨ \lor ∨\) 是析取(或逻辑加/并)运算。即「顶点 \(v_i\)到达\(v_j\)有长度为零的路、或有长度为1 的路、……、或有长度为 \(n−1\) 的路」,这些路可能是通路、可能不是,但其中至少存在一条通路。
【例4】设有向图D=(V,E),请回答下列问题。

(1)图 D 中\(v_1\)到\(v_3\) 长度为3的通路有多少条?
(2)图 D 是哪种类型的连通图?
解:
(1) D 的邻接矩阵及其幂次为:
| \(A^0\) | \(A^1\) | \(A^2\) | \(A^3\) |
|---|---|---|---|
| $\begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} $ | \(\begin{bmatrix} 0 & 1 & 1 & 1\\\ 1 & 0 & 1 & 0\\ 0 & 0 & 0 & 1\\ 0 & 0 & 0 & 0 \end{bmatrix}\) | \(\begin{bmatrix} 1 & 0 & 1 & 1 \\ 0 & 1 & 1 & 2 \\ 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 \end{bmatrix}\) | \(\begin{bmatrix} 0 & 1 & 1 & 2\\ 1 & 0 & 1 & 1\\ 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 \end{bmatrix}\) |
由 \(A^3[1][4] = 2\) 知, $v_1 $ 到\(v_4\) 共有两条长度为3的路,计算过程如下:
\begin{aligned} A^3[1][4] &= A^2[1][1] \times A[1][4] + A^2[1][2] \times A[2][4] \\ &+ A^2[1][3] \times A[3][4] + A^2[1][4] \times A[4][4] \\ &= 1 \times 1 + 0 \times 0 + 1 \times 1 + 1 \times 0 = 2 \end{aligned}
\begin{aligned} A^2[1][1] &= A[1][1] \times A[1][1] + A[1][2] \times A[2][1] \\ &+ A[1][3] \times A[3][1] + A[1][4] \times A[4][1] \\ &= 0 \times 0 + 1 \times 1 + 1 \times 0 + 1 \times 0 = 1 \end{aligned}
\begin{aligned} A^2[1][3] &= A[1][1] \times A[1][3] + A[1][2] \times A[2][3] \\ &+ A[1][3] \times A[3][3] + A[1][4] \times A[4][3] \\ &= 0 \times 1 + 1 \times 1 + 1 \times 0 + 1 \times 0 = 1
\end{aligned}
即这两条长度为 3 的路为\((v_1,v_2, v_1, v_4)\)和\((v_1,v_2, v_3, v_4)\) 。其中\((v_1,v_2, v_3, v_4)\) 是一条通路,所以 D 中 \(v_1\)到\(v_4\)长度为 3的通路有一条。
(2)计算 D 的可达矩阵。显然D 不是强连通的,因为\(v_3\)到 $ v_1$是不可达的;D是单侧连通的(即对于任意顶点偶对,至少一个节点到另一个节点是可达的)。
| \(P\) | \(P^T\) | \(P\or P^T\) |
|---|---|---|
| \(P = A^0 \lor A^1 \lor A^2 \lor A^3 =\begin{bmatrix} 1 & 1 & 1 & 1 \\ 1 & 1 & 1 & 1 \\0 & 0 & 1 & 1 \\ 0 & 0 & 0 & 1 \end{bmatrix}\) | \(\begin{bmatrix} 1 & 1 & 0 & 0 \\ 1 & 1 & 0 & 0 \\ 1 & 1 & 1 & 0 \\ 1 & 1 & 1 & 1 \end{bmatrix}\) | \(\begin{bmatrix} 1 & 1 & 1 & 1 \\ 1 & 1 & 1 & 1 \\ 1 & 1 & 1 & 1 \\ 1 & 1 & 1 & 1 \end{bmatrix}\) |
三、赋权矩阵
加权有向图的带权邻接矩阵
若为有向图D=(V,E)的每条边赋予一个权数,则称D为加权有向图。
设D=(V,E)是一个简单加权有向图,$V={ν_1,ν_2,...,ν_n\},则D的邻接矩阵 \(A=(a_{ij})_{n×n}\),其中
【例5】给出有向图D=(V,E)的赋权矩阵。
| 图D | 权矩阵 |
|---|---|
 |
 |
四、关联矩阵
4.1 无向图的关联矩阵
设 G=(V,E)是一个无向图,\(V=\{v_1,v_2,...,v_n\}\),\(E=\{e_1,e_2,...,e_m \}\),则 G的关联矩阵 \(M=(m_{ij})_{n×m}\),
其中
无向图的关联矩阵每一列的元素之和为2,且第\(i\)行的元素之和是\(ν_i\)的次数,简单图的关联矩阵是(0,1)矩阵。
【例6】给出无向图D=(V,E)的关联矩阵。
| 无向图 | 关联矩阵 |
|---|---|
 |
 |
4.2 有向图的关联矩阵
设 G=(V,E)是一个有向图,\(V=\{v_1,v_2,...,v_n\}\),\(E=\{e_1,e_2,...,e_m\}\),则 G的关联矩阵\(M=(m_{ij})_{n×m}\),
其中