4. 数学知识（I）

标签：10 le int cdots 数学知识 binom include

4.1 质数

4.1.1 试除法判定质数

模板：AcWing 866. 试除法判定质数

题目：给你 \(n\) 个正整数 \(a_i\)，判断其是否是质数。\(1\le n\le 100,1\le a_i\le 2^{31}-1\)。

思路：

根据质数的定义，可知若 \(2\sim a-1\) 之间的数都不能整除 \(a\)，则 \(a\) 为质数。那么遍历 \(2\sim a-1\) 之间的数，判断其能否整除 \(a\) 即可，时间复杂度 \(O(a)\)。

考虑优化。我们知道，若 \(p\mid a\)，则 \(\dfrac{a}{p}\mid a\)。所以我们可以只遍历 \(2\sim \sqrt{a}\) 之间的数即可。时间复杂度 \(O\left(n\sqrt{a}\right)\)。

代码：

#include <iostream>
#include <cstdio>
#include <algorithm>

using namespace std;

int n;

bool prime(int x) { // 判断x是否是质数
    if (x == 1) return 0; // 1既不是质数,也不是合数
    for (int i = 2; i <= x/i; ++i) // i<=n/i即i*i<=m
        if (x % i == 0) return 0;
    return 1; // 如果x不能被2~sqrt(x)之间的数整除,说明x是质数
}

int main() {
    scanf("%d", &n);
    while (n -- ) {
        int x;
        scanf("%d", &x);
        if (prime(x)) puts("Yes");
        else puts("No");
    }
    return 0;
}

4.1.2 分解质因数

模板：AcWing 867. 分解质因数

题目：给你 \(n\) 个整数 \(a_i\)，将其分解质因数，并按照质因子从小到大的顺序输出每个质因子的底数和指数。\(1\le n\le 100,2\le a_i\le 2\times 10^9\)。

思路：

与试除法类似地，我们枚举 \(i\in[2,\sqrt{a}]\)，若 \(i\mid a\) 则不断将 \(a\) 除以 \(i\)，直到 \(i\not\mid a\) 为止，同时用一个计数器 \(cnt\) 记录除的次数。那么 \(i\) 的指数即为 \(cnt\)，显然这样的 \(i\) 都是质数。最后若 \(a>1\)，说明 \(a\) 有一个大于 \(\sqrt{a}\) 的质因子，指数为 \(1\)，直接输出即可。

时间复杂度 \(O(n\sqrt{a})\)。

代码：

#include <iostream>
#include <cstdio>
#include <algorithm>

using namespace std;

int n, x;

int main() {
    scanf("%d", &n);
    while (n -- ) {
        scanf("%d", &x);
        for (int i = 2; i <= x/i; ++i) {
            if (x % i == 0) {
                int cnt = 0;
                while (x % i == 0) cnt ++, x /= i;
                printf("%d %d\n", i, cnt);
            }
        }
        if (x != 1) printf("%d 1\n", x);
        puts("");
    }
    return 0;
}

4.1.3 筛质数

模板：AcWing 868. 筛质数

题目：给你一个数 \(n\)，计算 \([1,n]\) 中质数的数量。\(1\le n\le 10^6\)。

4.1.3.1 埃氏筛

思路：

最朴素的埃氏筛出于这样的想法：我们从 \(2\) 开始枚举每一个数，用 \(st_i\) 存储数 \(i\) 是否被打上标记。若遍历到 \(i\) 时 \(st_i=0\)，说明 \(i\) 是质数，将其加入质数数组 \(prime\) 中；反之则说明 \(i\) 不是质数。接着我们枚举 \(i\) 的倍数，将它们都打上标记。

朴素的埃氏筛时间复杂度为 \(O(n\log n)\)。

我们考虑优化。由于一个合数的倍数必定被其质因子筛过了，所以我们只需要筛质数的倍数即可。时间复杂度 \(O(n\log \log n)\)。

核心代码：

int n;
int prime[N], cnt; 
bool st[N];

void Eratosthenes(int n) {
    st[1] = 1;
    for (int i = 2; i <= n; ++i) {
        if (!st[i]) {
            prime[++cnt] = i;
        	for (int j = i+i; j <= n; j += i) st[j] = 1;
        }
    }
}

4.1.3.2 线性筛

思路：

尽管改进版的埃氏筛已经很快了，但其仍然存在一个问题：例如，对于 \(15\)，\(3\) 会筛掉它，\(5\) 也会筛掉它，这样就造成了时间浪费。对于数 \(i\)，我们从第 \(1\) 个质数 \(2\) 开始循环，筛去质数与 \(i\) 的乘积。直到 \(i\bmod prime_j=0\) 时或 \(prime_j>n/i\) 时跳出。

由于每个数只会被筛一次，所以时间复杂度为 \(O(n)\)。

代码：

#include <iostream>
#include <cstdio>
#include <algorithm>

using namespace std;

const int N = 1e6+10;

int n;
int prime[N], cnt; 
bool st[N];

void Euler(int n) {
    st[1] = 1;
    for (int i = 2; i <= n; ++i) {
        if (!st[i]) prime[++cnt] = i;
        for (int j = 1; j <= cnt && prime[j] <= n/i; ++j) {
            st[i*prime[j]] = 1;
            if (i % prime[j] == 0) break;
        }
    }
}

int main() {
    scanf("%d", &n);
    Euler(n);
    printf("%d\n", cnt);
    return 0;
}

4.2 约数

4.2.1 试除法求约数

模板：AcWing 869. 试除法求约数

题目：给你 \(n\) 个整数 \(a_i\)，计算每个数的约数，按从小到大的顺序输出。\(1\le n\le 100,2\le a_i\le 2\times 10^9\)。

思路：基本和试除法的思路是相同的。我们用一个数组 \(fac\) 来存储 \(a_i\) 的因数。从 \(2\) 开始遍历到 \(\sqrt{a_i}\)，再倒序遍历 \(fac\) 输出 \(a_i/fac_i\) 即可。注意特判完全平方数。

时间复杂度 \(O(n\sqrt{a_i})\)

代码：

#include <iostream>
#include <cstdio>
#include <algorithm>

using namespace std;

const int N = 5e4+10;

int n, x;
int fac[N], idx;

int main() {
    scanf("%d", &n);
    while (n -- ) {
        scanf("%d", &x); idx = 0;
        for (int i = 1; i <= x/i; ++i) {
            if (x % i == 0)
                fac[++idx] = i, printf("%d ", i);
        }
        if ((long long)fac[idx]*fac[idx] == x) idx --;
        for (int i = idx; i >= 1; --i) printf("%d ", x/fac[i]);
        puts("");
    }
    return 0;
}

4.2.2 约数个数

模板：AcWing 870. 约数个数

题目：给定 \(n\) 个正整数 \(a_i\)，计算 \(\prod a_i\) 的约数个数对 \(10^9+7\) 取模的值。\(1\le n\le 100,1\le a_i\le 2\times 10^9\)。

思路：

考虑一个数 \(x\)，假设其质因数分解后得到的乘积为：

\[x=\prod_{i=1}^m p_i^{r_i}\tag{4.1} \]

其中，\(p_i\) 为质数，\(r_i\in\mathbb{N}_+\)，且 \(p_1<p_2<\cdots<p_m\)。

对于 \(x\) 的质因子 \(p_i\)，都有选 \(0\) 个，选 \(1\) 个，……选 \(r_i\) 个共 \(r_i+1\) 种选择。 由乘法原理，\(x\) 的质因数个数即为：

\[\prod_{i=1}^m(r_i+1)\tag{4.2} \]

在本题中，我们对于每个 \(a_i\) 先分解好质因数，最后乘起来即可。

代码：

#include <iostream>
#include <cstdio>
#include <algorithm>
#include <unordered_map>

using namespace std;

typedef long long ll;

const int P = 1e9+7;

unordered_map<int, int> p;

int n, x, ans = 1;

int main() {
    scanf("%d", &n);
    while (n -- ) {
        scanf("%d", &x);
        for (int i = 2; i <= x/i; ++i) {
            while (x % i == 0) 
                x /= i, p[i] ++;
        }
        if (x > 1) p[x] ++; 
    }
    
    for (auto i : p) ans = (ll)ans * (i.second + 1) % P;
    printf("%d\n", ans);
    return 0;
}

4.2.3 约数之和

模板：AcWing 871. 约数之和

题目：给定 \(n\) 个正整数 \(a_i\)，计算 \(\prod a_i\) 的约数之和对 \(10^9+7\) 取模的值。\(1\le n\le 100,1\le a_i\le 2\times 10^9\)。

思路：类似 4.2.2 中的思路。考虑一个数 \(x\)，假设其质因数分解后得到的乘积为：

\[x=\prod_{i=1}^m p_i^{r_i}\tag{4.3} \]

其中，\(p_i\) 为质数，\(r_i\in\mathbb{N}_+\)，且 \(p_1<p_2<\cdots<p_m\)。

由乘法原理，其约数之和为：

\[\prod_{i=1}^m\sum_{j=0}^{r_i} p_i^j\tag{4.4} \]

代码：

#include <iostream>
#include <cstdio>
#include <algorithm>
#include <unordered_map>

using namespace std;

const int mod = 1e9+7;

typedef long long ll;

unordered_map<int, int> p;

int n, x, ans = 1;

int main() {
    scanf("%d", &n);
    while (n -- ) {
        scanf("%d", &x);
        for (int i = 2; i <= x/i; ++i) {
            while (x % i == 0)
                x /= i, p[i] ++;
        }
        if (x > 1) p[x] ++; 
    }
    
    for (auto t : p) {
        int pr = t.first, num = t.second, tmp = 1;
        while (num -- ) tmp = ((ll)tmp * pr + 1) % mod;
        ans = (ll)ans * tmp % mod;
    }
    printf("%d\n", ans);
    return 0;
}

4.2.4 最大公约数（GCD）

定义：

若自然数 \(d\) 同时是自然数 \(a,b\) 的约数，则称 \(d\) 为 \(a,b\) 的公约数。在所有 \(a,b\) 的公约数中最大的一个，称为 \(a,b\) 的最大公约数，记作 \(\gcd(a,b)\)。

若自然数 \(m\) 同时是自然数 \(a,b\) 的倍数，则称 \(m\) 为 \(a,b\) 的公倍数。在所有 \(a,b\) 的公倍数中最小的一个，称为 \(a,b\) 的最小公倍数，记作 \(\text{lcm}(a,b)\)。

同理，我们也可以定义多个数的最大公约数和最小公倍数。

---

模板：AcWing 872. 最大公约数

题目：给定 \(n\) 个数对 \(a_i,b_i\)，计算 \(\gcd(a_i,b_i)\)。\(1\le n\le 10^5,1\le a_i,b_i\le 2\times 10^9\)。

思路：

九章算术·更相减损术：

\[\begin{aligned} & \forall a,b\in\mathbb{N},a\ge b,\; \gcd(a,b) = \gcd(b,a-b)\\ \end{aligned} \]

证明：

对于 \(a,b\) 的任意公约数 \(d\)，由于 \(d\mid a,d\mid b\)，所以 \(d\mid a-b\)，因此 \(d\) 也是 \(b,a-b\) 的公约数。故 \(a,b\) 的公约数集合与 \(b,a-b\) 的公约数集合相同，因此它们的最大公约数也相同。

证毕。

欧几里得算法：

\[\begin{aligned} & \forall a,b\in\mathbb{N},b\ne 0,\; \gcd(a,b) = \gcd(b,a\bmod b)\\ \end{aligned} \]

证明：

当 \(a<b\) 时，\(a\bmod b=a\)，命题成立。

当 \(a\ge b\) 时，不妨设 \(a=q\times b+r\)，其中 \(q,r\in\mathbb{N},0\le r<b\)，则 \(a\bmod b=r\)。对于 \(a,b\) 的任意公约数 \(d\)，由于 \(d\mid a,d\mid q\times b\)。所以 \(d\mid (a-qb)\)，即 \(d\mid r\)，因此 \(d\) 也是 \(b,a\bmod b\) 的公约数。 \(a,b\) 的公约数集合与 \(b,a\bmod b\) 的公约数集合相同，因此它们的最大公约数也相同。 命题成立。

证毕。

代码：

#include <iostream>
#include <cstdio>
#include <algorithm>

using namespace std;

int n, a, b;

int gcd(int a, int b) {
    if (!b) return a;
    return gcd(b, a%b); 
}

int main() {
    scanf("%d", &n);
    while (n -- ) {
        scanf("%d%d", &a, &b);
        printf("%d\n", gcd(a, b));
    }
    return 0;
}

4.3 欧拉函数

定义：

\(\forall a,b\in\mathbb{N}\)，若 \(\gcd(a,b)=1\)，则称 \(a,b\) 互质。同理，若 \(\gcd(a,b,c)=1\)，则称 \(a,b,c\) 互质。若 \(\gcd(a,b)=\gcd(a,c)=\gcd(b,c)\) 称为 \(a,b,c\) 两两互质。后者显然是一个更强的条件。

欧拉函数：

\(1\sim n\) 中与 \(n\) 互质的数的个数称为欧拉函数，记作 \(\varphi(n)\)。若在算数基本定理中，\(n=\prod_{i=1}^mp_i^{r_i}\)，则：

\[\varphi(n)=n\times\prod_{i=1}^m\left(1-\dfrac{1}{p_i}\right)\tag{4.5} \]

证明：

设 \(p\) 是 \(n\) 的质因子，则 \([1,n]\) 中 \(p\) 的倍数有 \(p,2p,3p,\cdots,(n/p)\times p\)，共 \(\dfrac{n}{p}\) 个。同理，若 \(q\) 也是 \(n\) 的质因子，则 \([1,n]\) 中 \(q\) 的倍数有 \(\dfrac n q\) 个。如果我们将这 \(\left(\dfrac n p+\dfrac n q\right)\) 个数去掉，则 \(pq\) 的倍数都被排除了两次，需要加回来一次。因此，\([1,n]\) 中不包含质因子 \(p,q\) 的数的个数为：

\[n-\left(\dfrac n p+\dfrac n q-\dfrac n {pq}\right)=n\left(1-\dfrac 1 p -\dfrac 1 q+\dfrac 1 {pq}\right)=n\left(1-\dfrac 1 p\right)\left(1-\dfrac 1 q\right)\tag{4.6} \]

类似地，对 \(n\) 的所有质因数使用容斥原理，即可得到 \((4.5)\)。

证毕。

4.3.1 分解质因数求欧拉函数

例题：AcWing 873. 欧拉函数

题目：给定 \(n\) 个正整数 \(a_i\)，计算 \(\varphi(a_i)\)。\(1\le n\le 100,1\le a_i\le 2\times 10^9\)。

思路：根据欧拉函数的计算方式，可以将 \(a_i\) 分解质因数计算 \(\varphi(a_i)\)。时间复杂度 \(O(n\sqrt{a_i})\)。

代码：

#include <iostream>
#include <cstdio>
#include <algorithm>

using namespace std;

int n, x;

int get_euler(int x) {
    int ans = x;
    for (int i = 2; i <= x/i; ++i) {
        bool check = 0;
        while (x % i == 0) {
            x /= i;
            check = 1;
        }
        if (check) ans = ans / i * (i-1);
    }
    if (x > 1) ans = ans / x * (x-1);
    return ans;
}

int main() {
    scanf("%d", &n);
    while (n -- ) {
        scanf("%d", &x);
        int ans = get_euler(x);
        printf("%d\n", ans);
    }
    return 0;
}

4.3.2 线性筛求欧拉函数

积性函数：

若 \(a,b\) 互质时，有 \(f(ab)=f(a)\times f(b)\)，则称函数 \(f\) 为积性函数。

积性函数的性质：

若 \(f\) 是积性函数，且在算数基本定理中 \(n=\prod_{i=1}^mp_i^{r_i}\)，则 \(f(n)=\prod_{i=1}^mf(p_i^{r_i})\)。证明很显然，因为 \(n\) 的质因数两两互质，由积性函数的定义显然成立。

欧拉函数的性质：

1. \(\forall n>1\)，\(1\sim n\) 中与 \(n\) 互质的数的和为 \(\dfrac{n\varphi(n)}{2}\)。

证明：

由于 \(\gcd(n,x)=\gcd(n,n-x)\)，所以与 \(n\) 不互质的数总是成对出现，且平均数为 \(\dfrac{n}{2}\)。因此，与 \(n\) 互质的数的平均数也为 \(\dfrac n2\)，那么 \(1\sim n\) 中与 \(n\) 互质的数的和即为 \(\dfrac{n\varphi(n)}{2}\)。

证毕。

2. 欧拉函数是积性函数。即若 \(a,b\) 互质，有 \(\varphi(ab)=\varphi(a)\times\varphi(b)\)。

将 \(a,b\) 分别分解质因数，根据欧拉函数的计算方法即可证明。

3. 设 \(p\) 为质数， 若 \(p\mid n\) 且 \(p^2\mid n\)，则 \(\varphi(n)=\varphi(n/p)\times p\)。

由于 \(n\) 与 \(n/p\) 都包含质因子 \(p\)，根据欧拉函数的计算方式即可证明。

4. 设 \(p\) 为质数，若 \(p\mid n\) 但 \(p^2 \not\mid n\)，则 \(\varphi(n)=\varphi(n/p)\times (p-1)\)。

因为 \(p\) 为质数，所以 \(\varphi(p)=p-1\)。又因为欧拉函数是积性函数，且 \(p,n/p\) 互质，所以 \(\varphi(n)=\varphi(n/p)\times (p-1)\)。

5. \(\sum_{d\mid n}\varphi(d)=n\)。

证明：

设 \(f(n)=\sum_{d\mid n}\varphi(d)\)。若 \(n,m\) 互质，由乘法分配律展开有 \(f(nm)=\sum_{d|nm}\varphi(d)=\sum_{d|n}\varphi(d)\sum_{d|m}\varphi(d)=f(n)f(m)\)。即 \(f\) 为积性函数。

由性质 3，易得 \(\varphi(p^i)=p^{i-1}(p-1)=p^i-p^{i-1}\)，其中 \(i>1\)。对于单个质因子 \(p\)，有：

\[f(p^r)=\sum_{d|p^r}\varphi(d)=\sum_{i=0}^r \varphi(p^i)=1+(p-1)+(p^2-p)+\cdots+(p^r-p^{r-1})=p^r\tag{4.7} \]

设在算数基本定理中，\(n=\prod_{i=1}^k p_i^{r_i}\)，有：

\[f(n)=f\left(\prod_{i=1}^k p_i^{r_i}\right)=\prod_{i=1}^kf(p_i^{r_i})=\prod_{i=1}^kp_i^{r_i}=n\tag{4.8} \]

得证。

---

模板：AcWing 874. 筛法求欧拉函数

题目：计算 \(1\sim n\) 中所有数的欧拉函数之和。\(1\le n\le 10^6\)。

思路：在线性筛的基础上，利用性质 3，4 即可。

代码：

#include <iostream>
#include <cstdio>
#include <algorithm>

using namespace std;

typedef long long ll;

const int N = 1e6+10;

int n; ll sum = 1;
int phi[N];
bool st[N];
int prime[N], cnt;

void get_Euler(int n) {
    phi[1] = 1, st[1] = 1;
    for (int i = 2; i <= n; ++i) {
        if (!st[i]) prime[cnt ++] = i, phi[i] = i-1;
        for (int j = 0; prime[j] <= n/i && j < cnt; ++j) {
            st[i*prime[j]] = 1;
            if (i % prime[j] == 0) {
                phi[i*prime[j]] = phi[i] * prime[j];
                break;
            }
            phi[i*prime[j]] = phi[i] * (prime[j]-1);
        }
        sum += (ll)phi[i];
    }
}

int main() {
    scanf("%d", &n);
    get_Euler(n);
    printf("%lld\n", sum);
    return 0;
}

4.4 快速幂

模板：AcWing 875. 快速幂

题目：给定 \(n\) 组 \(a_i,b_i,p_i\)，计算 \(a_i^{b_i}\bmod p_i\) 的值。\(1\le n\le 10^5,1\le a_i,b_i,p_i\le 2\times 10^9\)。

思路：

我们知道，每一个正整数可以唯一表示成若干个指数不重复的 \(2\) 的次幂之和（相当于转换为二进制）。设 \(b\) 在二进制表示下有 \(k\) 位，其中第 \(i\;(0\le i<k)\) 位的数是 \(c_i\;(c_i\in\{0,1\})\)，那么：

\[b=\sum_{i=0}^{k-1}c_{i}2^{i}\tag{4.9} \]

于是有：

\[a^b=a^{\sum_{i=0}^{k-1}c_{i}2^{i}}=\prod_{i=0}^{k-1}a^{c_i2^i}\tag{4.10} \]

又因为 ：

\[a^{2^i}=\left ( a^{2^{i-1}} \right )^2 \tag{4.11} \]

所以我们可以通过递推来求出每个乘积项。时间复杂度 \(O(n\log b)\)。

代码：

#include <iostream>
#include <cstdio>
#include <algorithm>

using namespace std;

typedef long long ll;

int n, a, b, p;

int power(int a, int b, int p) {
    int ans = 1;
    while (b) {
        if (b & 1) ans = (ll)ans * a % p;
        a = (ll)a * a % p;
        b >>= 1;
    }
    return ans;
}

int main() {
    scanf("%d", &n);
    while (n -- ) {
        scanf("%d%d%d", &a, &b, &p);
        printf("%d\n", power(a, b, p));
    }
    return 0;
}

4.5 乘法逆元

4.5.1 快速幂求乘法逆元

同余：若整数 \(a\) 与整数 \(b\) 除以正整数 \(m\) 的余数相等，则称 \(a,b\) 模 \(m\) 同余，记作 \(a\equiv b\pmod m\)。

同余系与剩余系：

对于 \(\forall a\in[0,m-1]\)，集合 \(\{a+km\}\;(k\in\mathbb{Z})\) 的所有数模 \(m\) 同余，余数均为 \(a\)。该集合称为一个模 \(m\) 的同余类，记作 \(\bar a\)。模 \(m\) 的同余类一共有 \(m\) 个，分别为 $\bar 0,\bar 1,\cdots,\overline{m-1} $，它们构成 \(m\) 的完全剩余系。\([1,m]\) 中与 \(m\) 互质的数共有 \(\varphi(m)\) 个，它们构成 \(m\) 的简化剩余系。

简化剩余系关于模 \(m\) 乘法封闭。因为若 \(a,b\;(0\le a,b<m)\) 与 \(m\) 互质，则 \(ab\) 显然也与 \(m\) 互质，则 \(ab\bmod m\) 也与 \(m\) 互质。即 \(ab\bmod m\) 也属于 \(m\) 的简化剩余系。

乘法逆元：若 \(ax\equiv 1\pmod m\)，则称 \(x\) 是 \(a\) 模 \(m\) 意义下的乘法逆元。记作 \(x=a^{-1}\)。

费马小定理：若 \(p\) 为质数，则 \(\forall a\in\mathbb{N}_+\)，有 \(a^{p}\equiv a\pmod p\)。

欧拉定理：若 \(a,p\) 互质，则 \(a^{\varphi(p)}\equiv 1\pmod p\)。

证明：

设 \(\{\overline{a_1},\overline{a_2},\cdots,\overline{a_{\varphi(p)}}\}\) 为 \(p\) 的简化剩余系。\(\forall 1\le i,j\le \varphi(p)\)，若 \(aa_i\equiv aa_j\pmod p\)，则 \(a(a_i-a_j)\equiv 0\pmod p\)。因为 \(a,p\) 互质，所以 \(a_i-a_j\equiv 0\pmod p\)，即 \(a_i\equiv a_j\pmod p\)。故当 \(i\ne j\) 时，\(\overline{aa_i},\overline{aa_j}\) 也代表不同的同余类。

又因为简化剩余系关于模 \(p\) 乘法封闭，所以 \(\overline{aa_i}\) 也在 \(p\) 的简化剩余系中。因此，集合 \(\{\overline{a_1},\overline{a_2},\cdots,\overline{a_{\varphi(p)}}\}\) 与集合 \(\{\overline{aa_1},\overline{aa_2},\cdots,\overline{aa_{\varphi(p)}}\}\) 都能表示 \(p\) 的简化剩余系。因此：

\[a^{\varphi(p)}a_1a_2\cdots a_{\varphi(p)}\equiv (aa_1)(aa_2)\cdots(aa_{\varphi(p)})\equiv a_1a_2\cdots a_{\varphi(p)}\pmod p\tag{4.12} \]

所以有 \(a^{\varphi(p)}\equiv 1\pmod p\)。欧拉定理成立。

当 \(p\) 为质数时，\(\varphi(p)=p-1\)。若 \(a\) 不为 \(p\) 的倍数，则 \(a^{p-1}\equiv 1\pmod p\)，那么 \(a^p\equiv a\pmod p\)。若 \(a\) 为 \(p\) 的倍数，费马小定理显然成立。

得证。

---

模板：AcWing 876. 快速幂求逆元

例题：给定 \(n\) 组 \(a_i,p_i\)，求 \(a_i\) 模 \(p_i\) 意义下的乘法逆元。若逆元不存在则输出 impossible。请输出 \(1\sim p_i-1\) 间的逆元。\(1\le n\le 10^5,1\le a_i,p_i\le 2\times 10^9\)，保证 \(p_i\) 为质数。

思路：

由费马小定理，可得 \(a^p\equiv a\pmod p\)。所以当 \(a\) 不为 \(p\) 的倍数时，有 \(a\cdot a^{p-2}\equiv 1\pmod p\)，即 \(a^{p-2}\) 即为 \(a\) 模 \(p\) 意义下的乘法逆元。当 \(a\) 为 \(p\) 的倍数时，乘法逆元不存在。

代码：

#include <iostream>
#include <cstdio>
#include <algorithm>

using namespace std;

typedef long long ll;

int n, a, p;

int power(int a, int b, int p) {
    int ans = 1;
    while (b) {
        if (b & 1) ans = (ll)ans * a % p;
        a = (ll)a * a % p;
        b >>= 1;
    }
    return ans;
}

int main() {
    scanf("%d", &n);
    while (n -- ) {
        scanf("%d%d", &a, &p);
        if (a % p == 0) puts("impossible");
        else printf("%d\n", power(a, p-2, p));
    }
    return 0;
}

4.5.2 线性递推求逆元

模板：P3811 【模板】乘法逆元

题目：给定 \(n,p\)，计算 \([1,n]\) 中所有整数模 \(p\) 意义下的乘法逆元。\(1\le n\le 3\times 10^6,n<p<20000528\)，保证 \(p\) 为质数。

思路：

首先我们有 \(1^{-1}\equiv 1\pmod p\)。

设 \(p=ki+r\;(1<r<i<p)\)，则 \(ki+r\equiv 0\pmod p\)，两边同乘 \(i^{-1},r^{-1}\)，得到 \(kr^{-1}+i^{-1}\equiv 0\pmod p\)，所以有：

\[i^{-1}\equiv -kr^{-1}\equiv - \left \lfloor \dfrac{p}{i} \right \rfloor(p\bmod i)^{-1}\pmod p\tag{4.13} \]

代码：

#include <iostream>
#include <cstdio>
#include <algorithm>

using namespace std;

typedef long long ll;

const int N = 3e6+10;

int n, p;
int inv[N];

int main() {
    scanf("%d%d", &n, &p);
    inv[1] = 1; puts("1");
    for (int i = 2; i <= n; ++i) {
        inv[i] = ((ll)p - (ll)(p/i) * inv[p%i] % p + p) % p;
        printf("%d\n", inv[i]);
    }
    return 0;
}

4.6 扩展欧几里得算法（ExGCD)

4.6.1 扩展欧几里得算法

裴蜀定理：对于任意整数 \(a,b\)，存在一对整数 \(x,y\)，满足 \(ax+by=\gcd(a,b)\)。

证明：

若 \(a,b\) 中有任何一个为 \(0\)，则 \(\gcd(a,b)=a\)。这时取 \(x=1,y=0\) 即可。

若 \(a,b\) 都不为 \(0\)，由于 \(\gcd(a,b)=\gcd(a,-b)\)，不妨设 \(a,b>0\)，则 \(\gcd(a,b)=\gcd(b,a\bmod b)\)。假设存在一对整数 \(x',y'\)，满足 \(bx'+(a\bmod b)\times y'=\gcd(b,a\bmod b)\)。因为 \(bx'+(a\bmod b)\times y'=bx'+(a-b\lfloor a/b\rfloor)y'=ay'+b(x'-\lfloor a/b\rfloor y')\)。那么令 \(x=y',y=x'-\lfloor a/b\rfloor y'\)，就有 \(ax+by=\gcd(a,b)\)。

对欧几里得算法的递归过程运用数学归纳法，可知裴蜀定理成立。

证毕。

对于更一般的方程 \(ax+by=c\)，其有解当且仅当 \(d\mid c\)。我们可以先求出 \(ax+by=d\) 的一组特解 \(x_0,y_0\)，那么 \(\dfrac c d x_0,\dfrac c d y_0\) 即为原方程的一组特解。

其通解可以表示为：

\[x=\dfrac c d x_0+k\dfrac bd,y=\dfrac c d y_0-k\dfrac a d\tag{4.14} \]

其中 \(k\in\mathbb{Z}\)。

---

模板：AcWing 877. 扩展欧几里得算法

题目：给定 \(n\) 对数 \(a_i,b_i\)，计算出一对整数 \(x,y\)，满足 \(ax+by=\gcd(a,b)\)。\(1\le n\le 10^5,1\le a_i,b_i\le 2\times 10^9\)。

思路：直接套用裴蜀定理求出原方程的一组特解即可。注意 exgcd 函数中的 \(x,y\) 是通过引用来传递的。

代码：

#include <iostream>
#include <cstdio>
#include <algorithm>

using namespace std;

int n, a, b, x, y;

int exgcd(int a, int b, int &x, int &y) {
    if (!b) {x = 1, y = 0; return a;}
    
    int d = exgcd(b, a%b, x, y);
    int t = y; 
    y = x - (a/b) * t, x = t;
    return d;
}

int main() {
    scanf("%d", &n);
    while (n -- ) {
        scanf("%d%d", &a, &b);
        x = 0, y = 0;
        int d = exgcd(a, b, x, y);
        printf("%d %d\n", x, y);
    } 
    return 0;
}

4.6.2 线性同余方程

模板：AcWing 878. 线性同余方程

题目：给定 \(n\) 组数据 \(a_i,b_i,m_i\)，求出一个整数 \(x_i\) 使得 \(a_i\times x_i\equiv b_i\pmod {m_i}\)，如果无解则输出 impossible。\(1\le n\le 10^5,1\le a_i,b_i,m_i\le 2\times 10^9\)，求出的 \(x_i\) 必须在 int 范围内。

思路：

原方程可化为 \(ax+my=b\;(y\in\mathbb{Z})\)，那么当且仅当 \(\gcd(a,m)\mid b\) 时，原方程有解。在有解时，先用扩展欧几里得算法求出一组解 \(x_0,y_0\) 满足 \(ax_0+my_0=\gcd(a,m)\)，则原方程的一个解 \(x=\dfrac{b}{\gcd(a,m)}x_0\)。

代码：

#include <iostream>
#include <cstdio>
#include <algorithm>

using namespace std;

typedef long long ll;

int n;
ll a, b, m;

ll exgcd(ll a, ll b, ll &x, ll &y) {
    if (!b) {x = 1, y = 0; return a;}
    
    ll d = exgcd(b, a%b, x, y);
    ll t = y;
    y = x - a / b * t, x = t;
    return d;
}

int main() {
    scanf("%d", &n);
    while (n -- ) {
        scanf("%lld%lld%lld", &a, &b, &m);
        if (b % __gcd(a, m)) {puts("impossible"); continue;}
        
        ll x, y;
        ll d = exgcd(a, m, x, y);
        printf("%lld\n", b/d*x%m);
    }
    return 0;
}

4.7 中国剩余定理

模板：AcWing 204. 表达整数的奇怪方式

题目：

给你 \(2n\) 个整数 \(a_1,a_2,a_3,...,a_n\) 和 \(m_1,m_2,m_3,...,m_n\)。

请你求出方程组

\[\left\{\begin{aligned} &x\equiv m_1\pmod {a_1}\\ &x\equiv m_2\pmod {a_2}\\ &\cdots \\ &x\equiv m_n\pmod {a_n} \end{aligned}\right.\tag{4.15} \]

的最小非负整数解。

若无解则输出 -1。

\(1\le n\le 25,1\le a_i\le 2^{31}-1,0\le m_i<a_i\)。保证 \(x\) 在 long long 范围内。

思路：

先考虑 \(n=2\) 的情形，即

\[\left\{\begin{aligned} &x\equiv m_1\pmod {a_1}\\ &x\equiv m_2\pmod {a_2} \end{aligned}\right.\tag{4.16} \]

它们可以改写为 \(x=a_1k_1+m_1=a_2k_2+m_2\;(k_1,k_2\in\mathbb{Z})\)。那么有 \(a_1k_1-a_2k_2=m_2-m_1\)。当 \(\gcd(a_1,a_2)\mid (m_2-m_1)\) 时，我们可以用扩展欧几里得算法求出 \(k_1\) 的一个特解。

所以，当原方程组有解时，\(x\) 的一个特解是 \(k_1a_1+m_1\)，通解是 \(\left( k_1+k\dfrac{a_2}{\gcd(a_1,a_2)}\right)a_1+m_1\;(k\in\mathbb{Z})\)。将括号拆开，可得 \(x=a_1k_1+k\dfrac{a_1a_2}{\gcd(a_1,a_2)}+m_1=k\text{lcm}(a,b)+a_1k_1+m_1\)。令 \(a_1k_1+m_1=m_0,\text{lcm}(a_1,a_2)=a_0\)，则 \(x=a_0k+m_0\)。

可以看到，最后 \(x\) 与开始时的方程的形式相同。那么对于 \(n>2\) 的情形，可以每次合并两个方程组来计算。

代码：

#include <iostream>
#include <cstdio>
#include <algorithm>

using namespace std;

#define int long long

int n, a1, m1, a2, m2;

int exgcd(int a, int b, int &x, int &y) {
    if (!b) {x = 1, y = 0; return a;}
    
    int d = exgcd(b, a%b, x, y);
    int t = y;
    y = x - a / b * t, x = t;
    return d;
}

signed main() {
    scanf("%lld", &n);
    scanf("%lld%lld", &a1, &m1);
    
    for (int i = 1; i < n; ++i) {
        scanf("%lld%lld", &a2, &m2);
        
        int k1, k2;
        int d = exgcd(a1, a2, k1, k2);
        if ((m2-m1) % d) puts("-1"), exit(0);
        
        k1 *= (m2 - m1) / d;
        int t = a2 / d;
        k1 = (k1 % t + t) % t; // 要求k1最小
        
        m1 = a1*k1 + m1, a1 = abs(a1*a2 / d); //a1要转为非负整数
    }
    printf("%lld\n", (m1%a1+a1)%a1);
    return 0;
}

4.8 高斯消元

4.8.1 高斯消元解线性方程组

模板：AcWing 883. 高斯消元解线性方程组

题目：

给定一个关于 \(x_i\) 的 \(n\) 元一次方程组

\[\left\{\begin{aligned} &a_{11}x_1+a_{12}x_2+\cdots+a_{1n}x_n=b_1\\ &a_{21}x_1+a_{22}x_2+\cdots+a_{2n}x_n=b_n\\ &\cdots\\ &a_{n1}x_1+a_{n2}x_2+\cdots+a_{nn}x_n=b_n \end{aligned}\right. \tag{4.17} \]

若其有且仅有一个解，将 \(x_i\) 保留两位小数后输出；若其有无数组解，输出 Infinite group solutions；若其无解，输出 No solution。\(1\le n\le 100,0\le |a_{ij}|,|b_i|\le 100\) 且均保留两位小数。

思路：

\((4.16)\) 可化为一个 \(n\) 行 \((n+1)\) 列的增广矩阵：

\[\begin{pmatrix} a_{11} & a_{12} & \cdots & a_{1n} & b_1\\ a_{21} & a_{22} & \cdots & a_{2n} & b_2\\ \vdots & & \vdots & & \vdots\\ a_{n1} & a_{n2} & \cdots & a_{nn} & b_n \end{pmatrix}\tag{4.18} \]

对于增广矩阵，我们需要了解它三种基本的变换方式：

1. 把某一行乘上一个非零的数；
2. 交换某两行；
3. 把某行的若干倍加到另一行去。

我们的目标，就是把 \((4.18)\) 化为一个阶梯型矩阵：

\[\begin{pmatrix} a_{11} & a_{12} & \cdots & a_{1n} & b_1\\ & a_{22} & \cdots & a_{2n} & b_2\\ & & \ddots & & \vdots\\ & & & a_{nn} & b_n\end{pmatrix}\tag{4.19} \]

在 \((4.18)\) 中，如果存在形如 \(0=d\;(d\ne 0)\) 的方程，说明原方程组存在矛盾，无解；如果存在形如 \(0=0\) 的方程，说明原方程组有无数组解；否则原方程组有无数组解，可以用代入消元法计算。

算法步骤：

设遍历到第 \(c\) 列第 \(r\) 行，\(c,r\) 初始时为 \(1\)。

重复以下四个步骤直到 \(c=n\)：

1. 找到第 \(c\) 列绝对值最大的一行，若这一行的第 \(c\) 列已经为 \(0\)，则 \(c\) 自增 \(1\)；
2. 将绝对值最大的行与第 \(r\) 行交换（第 2 种变换）；
3. 将当前行的第 \(c\) 列变为 \(1\)（第 1 种变换）；
4. 通过当前行将第 \(r\) 行下面的所有行的第 \(c\) 列都消成 \(0\)（第 3 种变换）。\(c,r\) 自增 \(1\)。

高斯消元的时间复杂度是 \(O(n^3)\)。

代码：

#include <iostream>
#include <iomanip>
#include <cstdio>
#include <algorithm>
#include <cmath>

using namespace std;

const int N = 110;
const double eps = 1e-6;

int n;
double a[N][N];

int gauss() {
    int c = 1, r = 1;
    for ( ; c <= n; ++c) {
        int t = r;
        for (int i = r+1; i <= n; ++i) { // 找到第c列绝对值最大的一行 
            if (fabs(a[i][c]) > fabs(a[t][c]))
                t = i;
        }
        
        if (fabs(a[t][c]) < eps) continue; // 如果当前这一列的绝对值都为0就跳过
        
        for (int i = c; i <= n+1; ++i) swap(a[t][i], a[r][i]); // 把第c列绝对值最大的一行换到第r行
        
        for (int i = n+1; i >= c; --i) a[r][i] /= a[r][c]; // 将第r行第c列消成1
        
        for (int i = r+1; i <= n; ++i) { // 将下面所有行的第c列消成0
            if (fabs(a[i][c]) > eps) {
                for (int j = n+1; j >= c; --j)
                    a[i][j] -= a[i][c] * a[r][j];
            }
        }
        
        r ++;
    }
    
    if (r <= n) { // 实际有效的方程不足n个
        for (int i = r; i <= n; ++i) {
            if (fabs(a[i][n+1]) > eps) // 若存在0=d的方程,无解
                return -1; 
        }
        return 2; // 有无穷多组解
    }
    
    for (int i = n; i >= 1; --i) { // 代入消元
        for (int j = i+1; j <= n+1; ++j) 
            a[i][n+1] -= a[i][j] * a[j][n+1];
    }
    return 1;
}

int main() {
    ios::sync_with_stdio(0);
    cin.tie(0), cout.tie(0);
    
    cin >> n;
    for (int i = 1; i <= n; ++i) {
        for (int j = 1; j <= n+1; ++j)
            cin >> a[i][j];
    }
    
    int t = gauss();
    if (t == -1) {
        puts("No solution");
    } else if (t == 2) {
        puts("Infinite group solutions");
    } else {
        for (int i = 1; i <= n; ++i) {
            if (fabs(a[i][n+1]) < eps)
                a[i][n+1] = 0.00;
            cout << fixed << setprecision(2) << a[i][n+1] << endl;
        }
    }
    return 0;
}

4.8.2 高斯消元解异或线性方程组

模板：AcWing 884. 高斯消元解异或线性方程组

题目：给定一个关于 \(x_i\) 的异或线性方程组：

\[\left\{\begin{aligned} &a_{11}x_1\oplus a_{12}x_2\oplus \cdots\oplus a_{1n}x_n=b_1\\ &a_{21}x_1\oplus a_{22}x_2\oplus \cdots\oplus a_{2n}x_n=b_n\\ &\cdots\\ &a_{n1}x_1\oplus a_{n2}x_2\oplus \cdots\oplus a_{nn}x_n=b_n \end{aligned}\right. \tag{4.20} \]

其中，\(\oplus\) 表示异或。\(1\le n\le 100,a_{ij},x_i\in\{0,1\}\)。

思路：由于异或是“不进位的加法”，所以解普通线性方程组的方法对异或线性方程组仍然使用。使用高斯消元计算即可。

代码：

#include <iostream>
#include <cstdio>
#include <algorithm>

using namespace std;

const int N = 110;

int n;
bool a[N][N];

int gauss() {
    int c = 1, r = 1;
    for ( ; c <= n; ++c) {
        int t = r;
        for (int i = r+1; i <= n; ++i) {
            if (a[i][c]) {
                t = i;
                break;
            }
        }
        
        if (!a[t][c]) continue;
        
        for (int i = c; i <= n+1; ++i) swap(a[r][i], a[t][i]);
        
        for (int i = r+1; i <= n; ++i) {
            if (a[i][c]) {
                for (int j = n+1; j >= c; --j)
                    a[i][j] ^= a[r][j];
            }
        }
        
        r ++;
    }
    
    if (r <= n) {
        for (int i = r; i <= n; ++i) {
            if (a[i][n+1])
                return -1;
        }
        return 2;
    }
    
    for (int i = n; i >= 1; --i) {
        for (int j = i+1; j <= n; ++j)
            a[i][n+1] ^= a[i][j] & a[j][n+1];
    }
}

int main() {
    scanf("%d", &n);
    for (int i = 1; i <= n; ++i) {
        for (int j = 1; j <= n+1; ++j)
            scanf("%d", &a[i][j]);
    }
    
    int t = gauss();
    if (t == -1) {
        puts("No solution");
    } else if (t == 2) {
        puts("Multiple sets of solutions");
    } else {
        for (int i = 1; i <= n; ++i)
            printf("%d\n", a[i][n+1]);
    }
    return 0;
}

4.9 组合数

加法原理：若完成一件事的方法有 \(n\) 类，其中第 \(i\) 类方法包括 \(a_i\) 种不同的方法，且这些方法互不重合，则完成这件事共有 \(a_1+a_2+\cdots+a_n\) 种不同的方法。

乘法原理：若完成一件事需要 \(n\) 个步骤，完成第 \(i\) 个步骤的不同的方法有 \(a_i\) 种，则完成这件事共有 \(a_1a_2\cdots a_n\) 种方法。

排列数：从 \(n\) 个不同元素中任取 \(m\) 个元素（\(m\le n\)）按照一定的顺序排成一列，叫做从 \(n\) 个不同元素中取出 \(m\) 个元素的一个排列；从 \(n\) 个不同元素中取出 \(m\) 个元素的所有排列的个数，叫做从 \(n\) 个不同元素中取出 \(m\) 个元素的排列数，记作 \(\text{A}^m_n\)。

其计算公式如下：

\[\text{A}^m_n=n(n-1)\cdots(n-m+1)=\dfrac{n!}{(n-m)!}\tag{4.21} \]

组合数：从 \(n\) 个不同元素中任取 \(m\) 个元素（\(m\le n\)）组成一个集合，叫做从 \(n\) 个不同元素中取出 \(m\) 个元素的一个组合；从 \(n\) 个不同元素中取出 \(m\) 个元素的所有组合的个数，叫做从 \(n\) 个不同元素中取出 \(m\) 个元素的组合数，记作 \(\text{C}^m_n\) 或 \(\binom{n}{m}\)。

其计算公式如下：

\[\binom{n}{m}=\dfrac{\text{A}^m_n}{m!}=\dfrac{n!}{m!(n-m)!}\tag{4.22} \]

特别地，我们规定，\(m>n\) 时，\(\text{A}_n^m=\text{C}_n^m=0\)。

4.9.1 递推式求组合数

模板：AcWing 885. 求组合数 I

题目：给定 \(n\) 组询问，每组询问给定两个整数 \(a,b\)，计算 \(\binom{a}{b}\bmod (10^9+7)\) 的值。\(1\le n\le 10^4,0\le b\le a\le 2000\)。

思路：

组合数有一个递推式：

\[\binom{n}{m}=\binom{n-1}{m}+\binom{n-1}{m-1}\tag{4.23} \]

我们可以感性理解一下：从 \(n\) 个物品中选 \(m\) 个物品，如果选了第 \(n\) 个物品，则还需要从剩下 \((n-1)\) 个物品中选 \((m-1)\) 个物品，即 \(\binom{n-1}{m-1}\)；如果没有选第 \(n\) 个物品，则需要从剩下 \((n-1)\) 个物品中选 \((m-1)\) 个物品，即 \(\binom{n}{m-1}\)。所以 \(\binom{n}{m}=\binom{n-1}{m}+\binom{n-1}{m-1}\tag{4.22}\)。

严谨地证明一下：

\[\binom{n-1}{m}+\binom{n-1}{m-1}=\dfrac{(n-1)!}{m!(n-m-1)!}+\dfrac{(n-1)!}{(m-1)!(n-m)!}=\dfrac{(n-1)!\cdot n }{m!(n-m)!}=\dfrac{n!}{m!(n-m)!}=\binom{n}{m} \]

另外还有一个小技巧：

\[\binom{n}{m}=\binom{n}{n-m}\tag{4.24} \]

递推计算组合数的时间复杂度是 \(O(n^2)\)。

代码：

#include <iostream>
#include <cstdio>
#include <algorithm>

using namespace std;

const int N = 2010, mod = 1e9+7;

int n, a, b;
int c[N][N];

int main() {
    c[0][0] = 1;
    for (int i = 1; i <= 2000; ++i) {
        c[i][0] = c[i][i] = 1;
        for (int j = 1; j <= i/2; ++j)
            c[i][j] = c[i][i-j] = (c[i-1][j]+c[i-1][j-1]) % mod;;
    }
    
    scanf("%d", &n);
    while (n -- ) {
        scanf("%d%d", &a, &b);
        printf("%d\n", c[a][b]);
    }
    return 0;
}

4.9.2 乘法逆元求组合数

模板：AcWing 886. 求组合数 II

题目：给定 \(n\) 组询问，每组询问给定两个整数 \(a,b\)，计算 \(\binom{a}{b}\bmod (10^9+7)\) 的值。\(1\le n\le 10^4,0\le b\le a\le 10^5\)。

思路：

我们直接从 \((4.22)\) 入手。由于模数 \(10^9+7\) 是质数，我们可以预处理出 \(1\sim 10^5\) 中每个数的阶乘 \(fac_i\) 及其逆元 \(\text{inv}(i)\)，对于每次询问，答案即为 \(fac_a\times \text{inv}(b) \times \text{inv}(a-b)\bmod (10^9+7)\)。

代码：

#include <iostream>
#include <cstdio>
#include <algorithm>

using namespace std;

typedef long long ll;

const int N = 1e5+10, mod = 1e9+7;

int n, a, b;
int fac[N], inv[N];

int power(int a, int b) {
    int res = 1;
    while (b) {
        if (b & 1) res = (ll)res * a % mod;
        a = (ll)a * a % mod;
        b >>= 1;
    }
    return res;
}

int main() {
    fac[0] = 1, inv[0] = 1;
    for (int i = 1; i <= 100000; ++i) {
        fac[i] = (ll)fac[i-1] * i % mod;
        inv[i] = power(fac[i], mod-2);
    }
    
    scanf("%d", &n);
    while (n -- ) {
        scanf("%d%d", &a, &b);
        int ans = (ll)fac[a] * inv[b] % mod * inv[a-b] % mod;
        printf("%d\n", ans);
    }
    return 0;
}

4.9.3 Lucas 定理求组合数

模板：AcWing 887. 求组合数 III

题目：给定 \(n\) 组询问，每组询问给定三个整数 \(a,b,p\)，计算 \(\binom{a}{b}\bmod p\) 的值。\(1\le n\le 20,0\le b\le a\le 10^{18},1\le p\le 10^5\) 且 \(p\) 为质数。

思路：

Lucas 定理：

\[\binom{n}{m}\equiv \binom{\lfloor n/p \rfloor}{\lfloor m/p\rfloor}\binom{n\bmod p}{m\bmod p}\pmod p\tag{4.25} \]

其适用于 \(a,b\) 很大但 \(p\) 相对较小的时候。

证明：

设 \(x\) 是任意小于 \(p\) 的正整数，那么：

\[\binom{p}{x}=\dfrac{p!}{x!(p-x)!}=\dfrac{p}{x}\cdot\dfrac{(p-1)!}{(x-1)!(p-x)!}=\dfrac{p}{x}\cdot\binom{p-1}{x-1}\tag{4.26} \]

由于 \(x<p\) 且 \(p\) 是质数，所以 \(x\) 存在模 \(p\) 意义下的逆元，所以：

\[\binom{p}{x}\equiv p\times\text{inv}(x)\times\binom{p-1}{x-1}\equiv 0\pmod p\tag{4.27} \]

由二项式定理，\((1+x)^p=\sum_{i=0}^p\binom{p}{i}x^i\)。由 \((4.27)\)，\(\binom{p}{x}\equiv[x=0\vee x=p]\pmod p\) ；所以 \((1+x)^p\equiv 1+x^p\pmod p\)。

设 \(m=q_mp+r_m,n=q_np+r_n\;(0\le r<p)\)。由二项式定理，\((1+x)^n=\sum_{i=0}^n\binom{n}{i}x^i\)，同时有：

\[\begin{aligned} (1+x)^n&=(1+x)^{q_np+r_n}\\ &=(1+x)^{q_np}\cdot (1+x)^{r_n}\\ &=[(1+x)^p]^{q_n}\cdot (1+x)^{r_n}\\ &\equiv (1+x^p)^{q_n}\cdot (1+x)^{r_n}\\ &=\sum_{i=0}^{q_n}\binom{q_n}{i}x^{pi}\cdot \sum_{i=0}^{r_n}\binom{r_n}{i}x^{i}\\ &=\sum_{i=0}^{q_n}\sum_{j=0}^{r_n} \binom{q_n}{i}\binom{r_n}{j}x^{pi+j}\pmod p \end{aligned}\tag{4.28} \]

注意到 \(j>r_n\) 时的项为 \(0\)，所以我们可以枚举 \(k=ip+j\)，则 \((4.28)\) 可化为 \((1+x)^n\equiv\sum_{k=0}^n\binom{q_n}{\lfloor k/p \rfloor}\binom{r_n}{k\bmod p}x^k\pmod p\)。

那么 \(\sum_{k=0}^n\binom{n}{k}x^k\equiv \sum_{k=0}^n\binom{q_n}{\lfloor k/p \rfloor}\binom{r_n}{k\bmod p}x^k\pmod p\)。对比系数，令 \(k=m\)，则 \(\binom{n}{m}\equiv\binom{\lfloor n/p\rfloor}{\lfloor m/p\rfloor}\binom{n\bmod p}{m\bmod p}\)。

得证。

代码：

#include <iostream>
#include <cstdio>
#include <algorithm>

using namespace std;

#define int long long

int n, a, b, p;

int power(int a, int b, int p) {
    int ans = 1;
    while (b) {
        if (b & 1) ans = (int)ans * a % p;
        a = (int)a * a % p;
        b >>= 1;
    }
    return ans;
}

int C(int a, int b, int p) { // 当a,b<p时,直接通过公式计算(a b)%p
    if (a < b) return 0;
    
    int res = 1;
    for (int i = a, j = 1; i > a-b, j <= b; --i, ++j)
        res = (int)res * i % p * power(j, p-2, p) % p;
    return res;
}

int Lucas(int a, int b, int p) {
    if (a < p && b < p) return C(a, b, p);
    return (int)Lucas(a/p, b/p, p) * C(a%p, b%p, p) % p;
}

signed main() {
    scanf("%lld", &n);
    while (n -- ) {
        scanf("%lld%lld%lld", &a, &b, &p);
        printf("%lld\n", Lucas(a, b, p));
    }
    return 0;
}

4.9.4 高精度求组合数

模板：AcWing 888. 求组合数 IV

题目：计算 \(\binom{a}{b}\) 的值。\(1\le b\le a\le 5000\)。

思路：

我们还是从 \((4.22)\) 入手，我们可以分别将 \(a!\) 和 \(b!,(a-b)!\) 分解质因数，令 \(v_p(a)=\sum_{i=1}^\infty \lfloor a/p^i \rfloor\) 表示质数 \(p\) 在 \(a!\) 中出现的次数，则答案即为 \(\prod p^{v_p(a)-v_p(b)-v_p(a-b)}\)，通过高精度乘法计算即可。

代码：

#include <iostream>
#include <cstdio>
#include <algorithm>
#include <unordered_map>
#include <vector>

using namespace std;

const int N = 5010;

int a, b;
int prime[N], cnt[N], idx; bool st[N];
vector<int> ans;

void get_primes(int n) { // 线性筛
    st[1] = 1;
    for (int i = 2; i <= n; ++i) {
        if (!st[i]) prime[++idx] = i;
        for (int j = 1; j <= idx && prime[j] <= n/i; ++j) {
            st[i*prime[j]] = 1;
            if (!(i % prime[j])) break;
        }
    }
}

int get(int a, int p) { // 计算 a! 中质因子 p 数量
    int cnt = 0;
    while (a) cnt += a/p, a /= p;
    return cnt;
}

vector<int> mul(vector<int> &A, int b) { // 高精乘低精
    int t = 0;
    vector<int> C;
    
    for (int i = 0; i < A.size() || t; ++i) {
        if (i < A.size()) t += A[i] * b;
        C.push_back(t % 10);
        t /= 10;
    }
    
    while (C.size() > 2 && C.back() == 0) C.pop_back();
    return C;
}

int main() {
    scanf("%d%d", &a, &b);
    
    get_primes(5000);
    
    for (int i = 1; i <= idx; ++i) cnt[i] += get(a, prime[i]) - get(b, prime[i]) - get(a-b, prime[i]);
    
    ans.push_back(1);
    for (int i = 1; i <= idx; ++i) for (int j = 1; j <= cnt[i]; ++j) ans = mul(ans, prime[i]);
    
    for (int i = ans.size()-1; i >= 0; --i) printf("%d", ans[i]);
    return 0;
}

4.9.5 Catalan 数

例题：AcWing 889. 满足条件的01序列

题目：给定 \(n\) 个 \(0\) 和 \(n\) 个 \(1\)，将它们按某种顺序排成一个长度为 \(2n\) 的序列，求出在这些序列中满足任意前缀序列中 \(0\) 的个数都不少于 \(1\) 的个数的序列数量，答案对 \(10^9+7\) 取模。\(1\le n\le 10^5\)。

思路：

我们将原题目转化为：在一个平面直角坐标系中，\(0\) 表示向上走，\(1\) 表示向右走，现在求从 \((0,0)\) 点出发，走到 \((n,n)\) 点且不经过直线 \(y=x+1\) 的路径数量。如果我们没有不能经过直线 \(y=x+1\) 的限制，则方案数为 \(\binom{2n}{n}\)（在 \(2n\) 个操作中选 \(n\) 个操作为 \(0\)）。我们可以将所有经过直线 \(y=x+1\) 的路径第一次经过该直线·的点之后的路径关于该直线做轴对称，由于点 \((n,n)\) 关于直线 \(y=x+1\) 的对称点是 \((n-1,n+1)\)，则其方案数为 \(\binom{2n}{n-1}\)（在 \(2n\) 个操作中选 \((n-1)\) 个操作为 \(0\)）。

用 \(H_n\) 表示满足条件的路径数量，则有：

\[H_n=\binom{2n}{n}-\binom{2n}{n-1}\tag{4.29} \]

可能不太好理解，我们举一个 \(n=6\) 时的例子：

图4-1

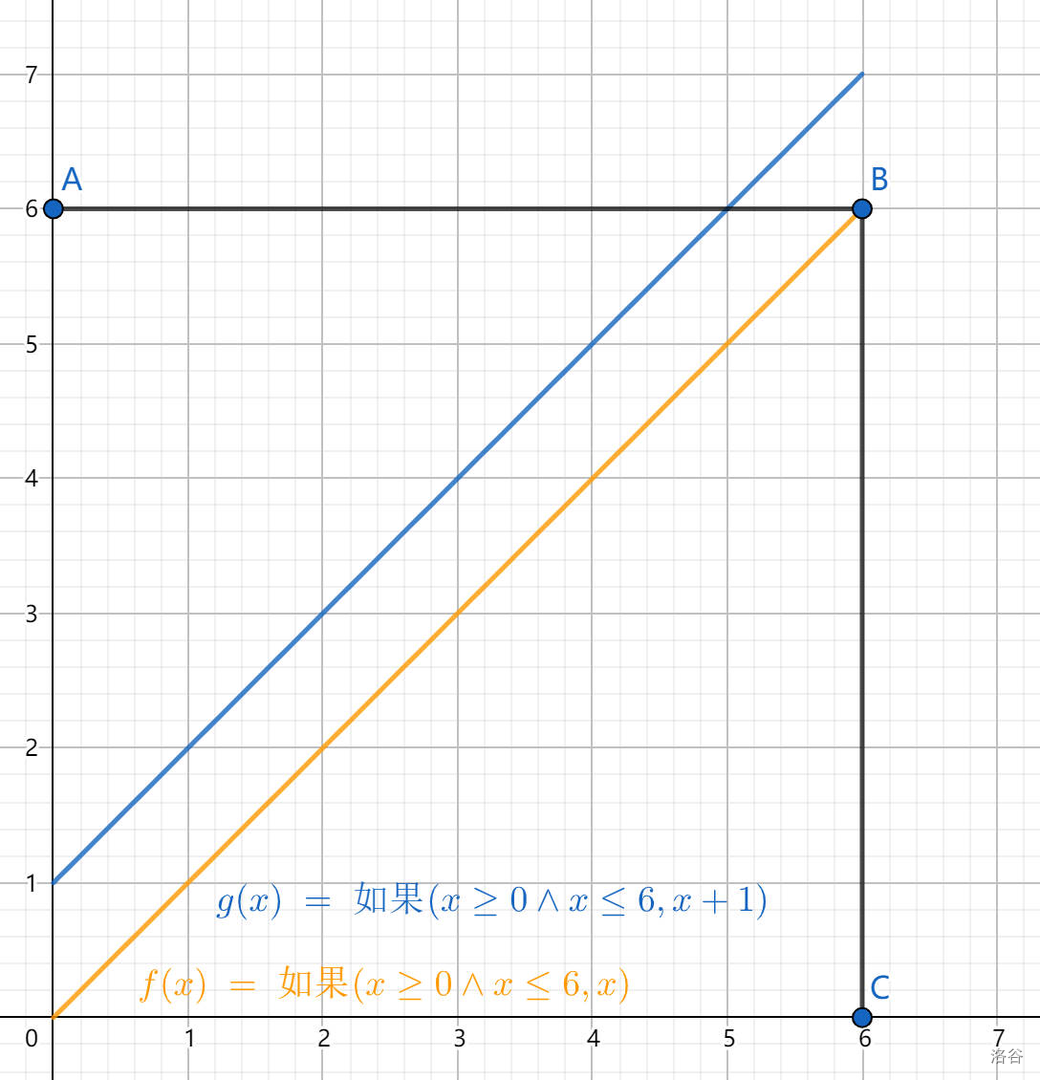
此时答案即为从 \((0,0)\) 走到 \((6,6)\) 的路径数量减去碰到蓝线的路径数量（这里的路径只能向上或向右走）。

假设一条碰到蓝线的路径如下图所示：

图4-2

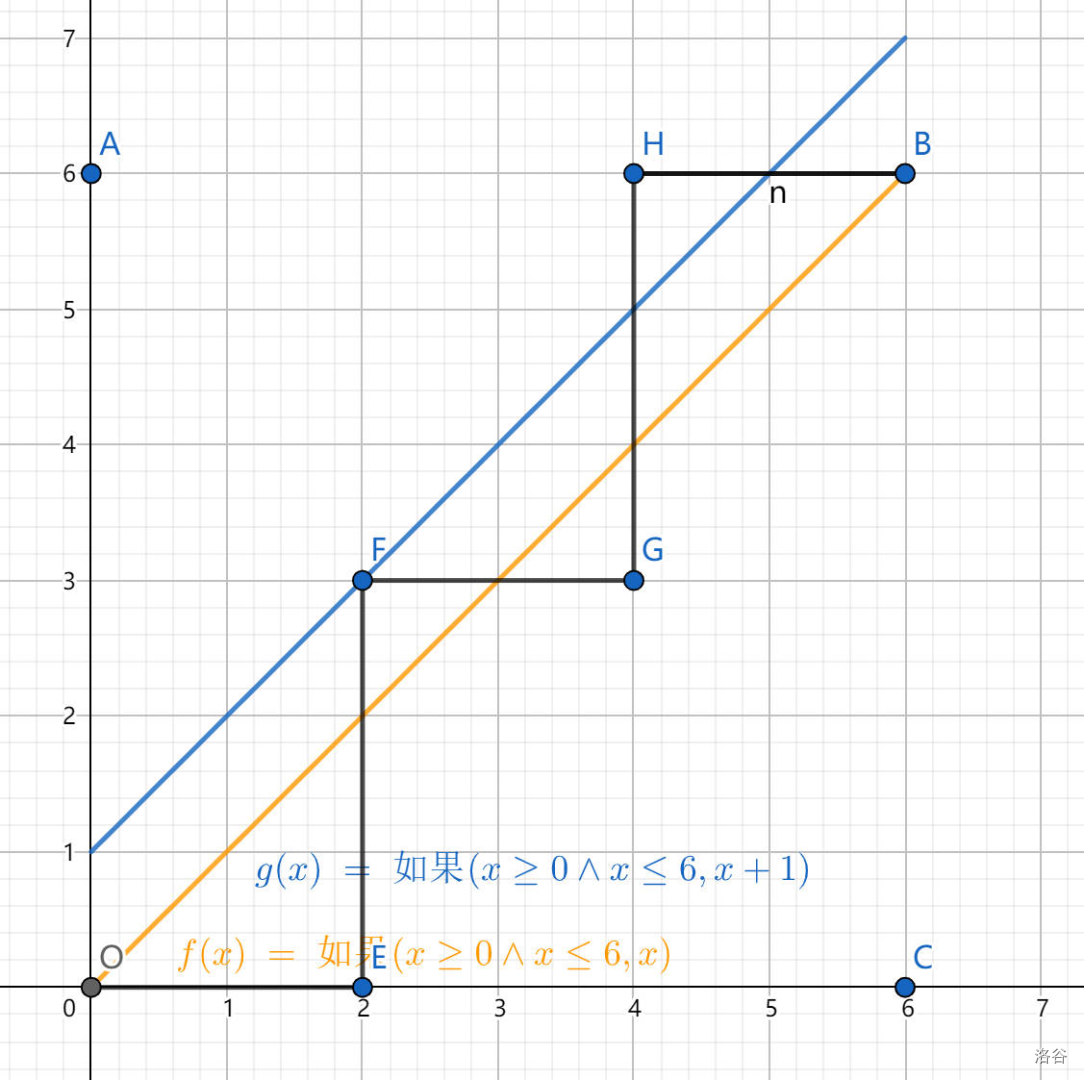
我们将其 \(F\) 点之后的路径关于蓝线做轴对称，得到的结果如下：

图4-3

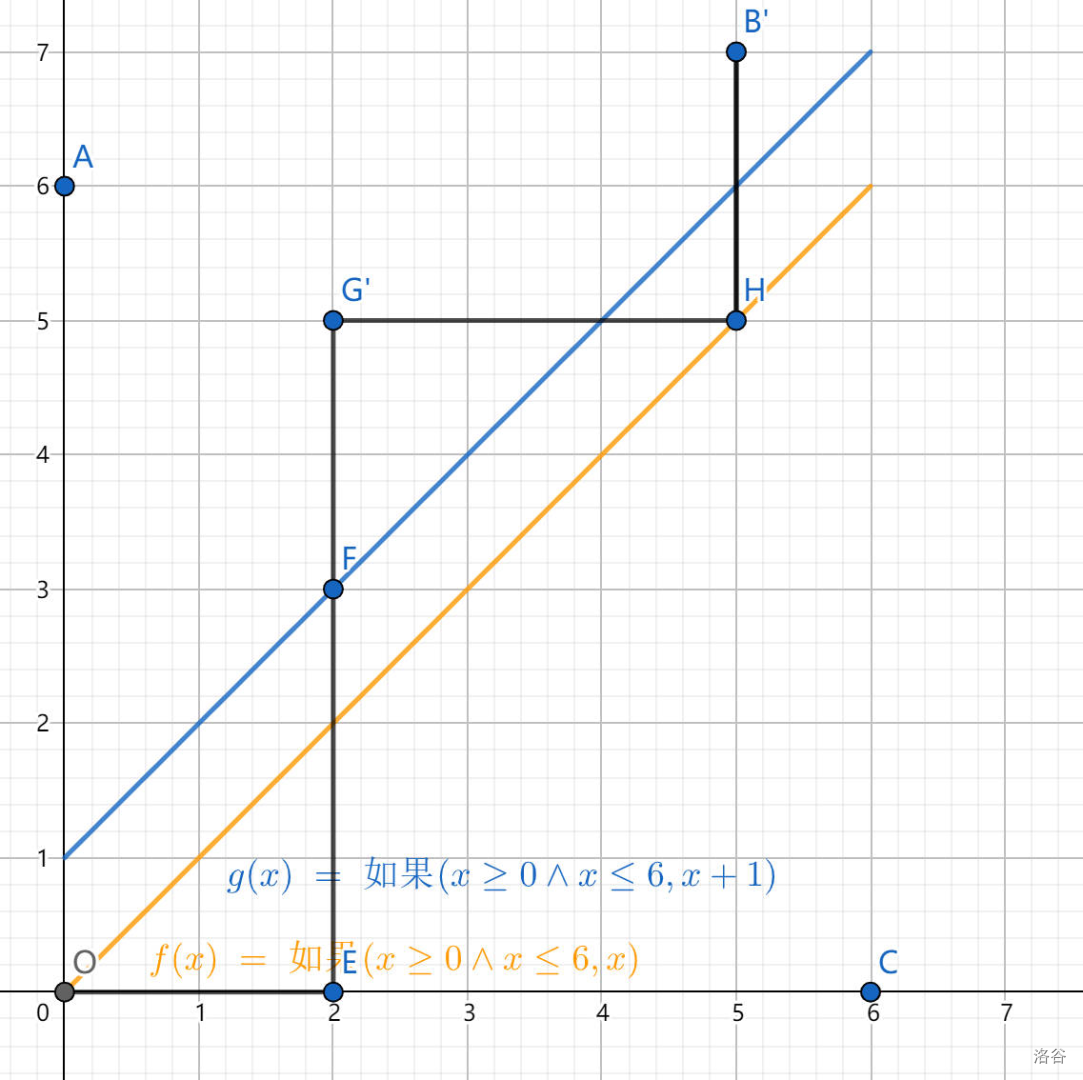
由于 \((6,6)\) 点关于直线 \(y=x+1\) 的对称点为 \((5,7)\)，所以任何一条不合法路径都可转化一条到达点 \((5,7)\) 的路径。那么满足条件的路径数量即为 \(\binom{12}{6}-\binom{12}{5}=132\)。

\(H_n\) 也就是卡特兰数，其前 \(6\) 项如下：

\(n\)	\(1\)	\(2\)	\(3\)	\(4\)	\(5\)	\(6\)
\(H_n\)	\(1\)	\(1\)	\(2\)	\(5\)	\(14\)	\(132\)

代码：

#include <iostream>
#include <cstdio>
#include <algorithm>

using namespace std;

typedef long long ll;

const int P = 1e9+7;

int n;

int power(int a, int b, int p) {
    int ans = 1;
    while (b) {
        if (b & 1) ans = (ll)ans * a % p;
        a = (ll)a * a % p;
    }
    return ans;
}

int C(int a, int b, int p) { 
    if (a < b) return 0;
    
    int res = 1;
    for (int i = a, j = 1; i > a-b, j <= b; --i, ++j)
        res = (ll)res * i % p * power(j, p-2, p) % p;
    return res;
}

int Lucas(int a, int b, int p) {
    if (a < p && b < p) return C(a, b, p);
    return (ll)Lucas(a/p, b/p, p) * C(a%p, b%p, p) % p;
}

int main() {
    scanf("%d", &n);
    ll ans = Lucas(2*n, n, P) - Lucas(2*n, n-1, P);
    ans = (ans % P + P) % P;
    printf("%lld\n", ans);
    return 0;
}

4.10 容斥原理

模板：AcWing 890. 能被整除的数

题目：给你一个数 \(n\) 和 \(m\) 个质数 \(p_1,p_2,\cdots,p_m\)，计算 \([1,n]\) 中能被 \(p_1,p_2,\cdots,p_m\) 中任意一个数整除的数的数量。\(1\le p_i,n\le 10^9,1\le m\le 16\)。

思路：

设 \([1,n]\) 中能被 \(p_i\) 整除的数的集合为 \(S_i\)。由容斥原理，答案即为：

\[\left | \bigcup_{i=1}^{m}S_i \right | = \sum_{i=1}^{m}(-1)^{i-1}\sum_{1\le j_1<j_2<\cdots <j_i\le m} \left | S_{j_1} \cap S_{j_2} \cap \cdots\ \cap S_{j_i} \right | \tag{4.30} \]

显然我们有 \(|S_i|=\lfloor n/p_i \rfloor\)，由于 \(p_1,p_2,\cdots,p_m\) 两两互质，所以 \(|S_{i_1}\cap S_{i_2}\cap \cdots\cap S_{i_j}|=\lfloor n/p_1p_2\cdots p_j \rfloor\)。

我们可以用二进制枚举 \((4.30)\) 中的并集，时间复杂度 \(O(2^m)\)。

代码：

#include <iostream>
#include <cstdio>
#include <algorithm>

using namespace std;

typedef long long ll;

const int N = 18;

int n, m, ans;
int p[N];

int main() {
    scanf("%d%d", &n, &m);
    for (int i = 1; i <= m; ++i) scanf("%d", &p[i]);

    for (int s = 1; s < (1 << m); s ++) {
        int t = 1, cnt = 0;
        for (int i = 1; i <= m; ++i) {
            if (!(s >> m-i & 1)) continue;
            if ((ll)t*p[i] > n) {t = -1; break;}
            
            t *= p[i], cnt ++;
        }
        
        if (t == -1) continue;
        ans += (cnt % 2) ? n/t : -n/t;
    }
    printf("%d\n", ans);
    return 0;
}

4.11 博弈论

公平组合游戏（ICG)：

若一个游戏满足：

• 由两名玩家交替行动；
• 在游戏进程的任意时刻，可以执行的合法行动与轮到哪名玩家无关；
• 不能行动的玩家判负。

则称该游戏为一个公平组合游戏。

4.11.1 Nim 游戏

模板：AcWing 891. Nim游戏

题目：有 \(n\) 堆石子，第 \(i\) 堆有 \(a_i\) 个石子。两名玩家轮流行动，每次可以任选一堆，取走任意多个石子，可把一堆取光，但不能不取。取走最后一个石子者获胜。假设双方都采取最佳策略，问先手能否必胜。\(1\le n\le 10^5,1\le a_i\le 10^9\)。

思路：

定理：NIM 游戏先手必胜，当且仅当 \(a_1\oplus a_2\oplus\cdots\oplus a_n\ne 0\)。其中 \(\oplus\) 表示异或。

证明：

所有物品被取光是一个必败局面。此时 \(a_1=a_2=\cdots=a_n=0\)，所以 \(a_1\oplus a_2\oplus\cdots\oplus a_n=0\)。

对于其他任意一个局面，若 \(a_1\oplus a_2\oplus \cdots\oplus a_n=x\ne 0\)，设 \(x\) 的二进制表示下最高位的 \(1\) 在第 \(k\) 位，则至少存在一堆石子 \(a_i\)，其第 \(k\) 位为 \(1\)。那么显然有 \(a_i\oplus x<x\)，那我们可以从第 \(i\) 堆石子中取走若干石子，使其变为 \(a_i\oplus x\)，则此时各堆石子数的异或结果为 \(0\)。

若 \(a_i\oplus a_2\oplus \cdots\oplus a_n=0\)，设存在一个取石子的方案使第 \(i\) 堆石子变为 \(a_i'\) 个，且 \(a_1\oplus a_2\oplus\cdots\oplus a_i'\oplus \cdots a_n=0\)，则 \(a_i=a_i'\)，与题目中不能不取的规定相违背。所以 \(a_i\oplus a_2\oplus \cdots\oplus a_n=0\) 时，无论采用何种行动，都会使得各堆石子数的异或结果变为正整数。

根据数学归纳法，可知 \(a_1\oplus a_2\oplus\cdots\oplus a_n\ne 0\) 时的局面为必胜局面，一定存在一种行动使得\(a_1\oplus a_2\oplus\cdots\oplus a_i'\oplus \cdots a_n=0\)，使对手进入必败局面。

证毕。

代码：

#include <iostream>
#include <cstdio>
#include <algorithm>

using namespace std;

int n, a, ans;

int main() {
    scanf("%d", &n);
    while (n -- ) {scanf("%d", &a); ans ^= a;}
    if (ans) puts("Yes");
    else puts("No");
    return 0;
}

例题：AcWing 892. 台阶-Nim游戏

题目：有一个 \(n\) 级台阶的楼梯，每级台阶上都有若干个石子，其中第 \(i\) 级台阶上有 \(a_i\) 个石子。两位玩家轮流操作，每次操作可以从任意一级台阶上拿若干个石子放到下一级台阶中（不能不拿）。已经拿到地面上的石子不能再拿，最后无法进行操作的人视为失败。问如果两人都采用最优策略，先手是否必胜。\(1\le n\le 10^5,1\le a_i\le 10^9\)。

思路：

结论：台阶游戏先手必胜，当且仅当奇数级台阶上的石子数异或结果不为 \(0\)。

证明：

当所有石子都被拿到地面上时，显然奇数级台阶上的石子数异或结果为 \(0\)。

对于其他任意一个局面，若奇数级台阶上的石子数异或结果不为 \(0\)，与经典 Nim 游戏中类似，必然存在一种方案使得奇数级台阶上的石子数异或结果为 \(0\)。

若奇数级台阶上的石子数异或结果为 \(0\)，分两类讨论：1. 移动奇数级台阶上的石子：与经典 Nim 游戏中类似，无论如何行动，都会将奇数级台阶上的石子数异或结果变为正整数。2. 移动偶数级台阶上的石子：则这个石子被移动到了奇数级台阶上，会将奇数级台阶上的石子数异或结果变为 \(1\)。所以，奇数级台阶上的石子数异或结果为 \(0\) 时，总会把奇数级台阶上的石子数异或结果不为 \(0\) 的局面给对手。

根据数学归纳法，可知奇数级台阶上的石子数异或结果不为 \(0\) 时，先手必胜，反之必败。

代码：

#include <iostream>
#include <cstdio>
#include <algorithm>

using namespace std;

int n, a, res;

int main() {
    scanf("%d", &n);
    for (int i = 1; i <= n; ++i) {
        scanf("%d", &a);
        if (i & 1) res ^= a;
    }
    if (res) puts("Yes");
    else puts("No");
    return 0;
}

4.11.2 有向图游戏

有向图游戏：给定一个有向无环图，图中有一个唯一的起点，在起点上放有一枚棋子，两名玩家交替地把这枚棋子沿有向边进行移动，每次可以移动一步，无法移动者判负。

任何一个公平组合游戏都可以被转化为一个有向图游戏，具体方法是：把每个局面看作图中的一个节点，并且从每个局面向沿者合法行动能够到达的下一个局面连有向边。

mex 运算：

设 \(S\) 表示一个非负整数集合。定义 \(\text{mex}(S)\) 表示最小的不属于 \(S\) 的非负整数。即：

\[\text{mex}(S)=\min_{x\in\mathbb{N},x\not\in S}\{x\}\tag{4.31} \]

SG 函数：

在有向图游戏中，对于一个节点 \(u\)，若其有 \(k\) 条出边，分别指向 \(v_1,v_2,\cdots,v_k\)。我们定义：

\[\text{SG}(u)=\text{mex}(\{\text{SG}(v_1),\text{SG}(v_2),\cdots,\text{SG}(v_k)\})\tag{4.32} \]

特别地，整个有向图游戏 \(G\) 的 SG 函数值被定义为有向图游戏起点 \(s\) 的 SG 函数值。即 \(\text{SG}(G)=\text{SG}(s)\)。

有向图游戏的和：

设 \(G_1,G_2,\cdots,G_n\) 为 \(n\) 个有向图游戏。定义有向图游戏 \(G\)，它的行动规则是任选某个有向图游戏 \(G_i\)，并在 \(G_i\)上行动一步。\(G\) 被称为有向图游戏 \(G_1,G_2,\cdots,G_n\) 的和。那么有：

\[\text{SG}(G)=\text{SG}(G_1)\oplus\text{SG}(G_2)\oplus\cdots\oplus \text{SG}(G_n)\tag{4.33} \]

定理：

有向图游戏的某个局面必胜，当且仅当该局面对应节点的 SG 函数值大于 \(0\)。

有向图游戏的某个局面必败，当且仅当该局面对应节点的 SG 函数值等于 \(0\)。

证明：

在一个没有出边的节点上，棋子不能移动，其 SG 值为 \(0\)，即为必败局面。

若一个节点的某个后继节点的 SG 值为 \(0\)，在 mex 运算后，该节点的 SG 值大于 \(0\)。这等价于若一个节点的后继节点中存在必败局面，则该节点对应的局面为必胜局面。

若一个节点的后继节点的 SG 值均不为 \(0\)，在 mex 运算后，该节点的 SG 值为 \(0\)。这等价于若一个节点的后继节点全部为必胜局面，则该节点对应的局面为必败局面。

多个有向图游戏可以用类似 NIM 游戏的方式证明。

例题：AcWing 893. 集合-Nim游戏

题目：给定 \(n\) 堆石子（每堆石子有 \(a_i\) 个）以及一个包含 \(k\) 个正整数的集合 \(S\)。有两个玩家轮流操作，每次操作可以从任意一堆石子中拿去 \(x\) 个石子，要求 \(x\in S\)，最后无法操作的人视为失败。若双方均采取最优策略，问先手能否获胜。\(1\le n,k\le 100,1\le a_i,S_i\le 10000\)。

思路：

我们可以用记忆化搜索计算 \(\text{SG}(i)\) 的值，代入 \((4.33)\) 计算即可。时间复杂度 \(O(ka_i)\)。

代码：

#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
#include <unordered_set>

using namespace std;

const int N = 110, M = 10010;

int n, k, ans;
int s[N], f[M];

int sg(int x) {
    if (f[x] != -1) return f[x];
    
    unordered_set<int> S;
    for (int i = 1; i <= k; ++i) {
        if (x < s[i]) continue;
        S.insert(sg(x-s[i]));
    }
    
    for (int i = 0; ; ++i) {
        if (!S.count(i))
            return f[x] = i;
    }
}

int main() {
    memset(f, -1, sizeof f);
    
    scanf("%d", &k);
    for (int i = 1; i <= k; ++i) scanf("%d", &s[i]);
    
    scanf("%d", &n);
    for (int i = 1; i <= n; ++i) {
        int x; scanf("%d", &x);
        ans ^= sg(x);
    }
    
    if (ans) puts("Yes");
    else puts("No");
    return 0;
}

例题：AcWing 894. 拆分-Nim游戏

题目：有 \(n\) 堆石子，第 \(i\) 堆有 \(a_i\) 个石子。两名玩家轮流行动，每次可以取走任意一堆石子，然后放入两堆规模更小的石子（加入石子的总数可以大于原来的石子数，但两堆的石子数都要小于原来的石子数，且新规模可以为 \(0\)）。取走最后一个石子者获胜。假设双方都采取最佳策略，问先手能否必胜。\(1\le n,a_i\le 100\)。

思路：

虽然石子的总数可能会变大，但最大值一定是不断减小的，所以游戏一定会结束。对于第 \(i\) 个石子，假设其分解为 \((b_i,b_j)\) 的形式，为保证不重复计算，不妨假设 \(b_i>b_j\)。由 SG 函数的性质，可知 \(\text{SG}(b_i,b_j)=\text{SG}(b_i)\oplus\text{SG}(b_j)\)。由此可以计算出 \(\text{SG}(a_i)\)。最后代入 \((4.33)\) 计算即可。

代码：

#include <iostream>
#include <cstdio>
#include <algorithm>
#include <unordered_set>
#include <cstring>

using namespace std;

const int N = 110;

int n, ans;
int f[N];

int sg(int x) {
    if (f[x] != -1) return f[x];
    
    unordered_set<int> S;
    for (int i = 0; i < x; ++i) {
        for (int j = 0; j <= i; ++j)
            S.insert(sg(i)^sg(j));
    }
    
    for (int i = 0; ; ++i) {
        if (!S.count(i))
            return f[x] = i;
    }
}

int main() {
    memset(f, -1, sizeof f);
    
    scanf("%d", &n);
    for (int i = 1; i <= n; ++i) {
        int x; scanf("%d", &x);
        ans ^= sg(x);
    }
    
    if (ans) puts("Yes");
    else puts("No");
    return 0;
}

标签：10,le,int,cdots,数学知识,binom,include
From： https://www.cnblogs.com/Jasper08/p/17461501.html