高斯消元法
高斯消元能在O(\(n^3\))的时间复杂度内求解n个方程,n个未知数的多元线性方程组,即
\[a_{11}x_{1}+a_{12}x_{2}+a_{13}x_{3}+\dots +a_{1n}x_{n} = b_{1}\\a_{21}x_{1}+a_{22}x_{2}+a_{23}x_{3}+\dots +a_{2n}x_{n} = b_{2}\\ \dots \\ a_{n1}x_{1}+a_{n2}x_{2}+a_{n3}x_{3}+\dots +a_{nn}x_{n} = b_{n} \]对增广矩阵做初等行列变换,变成一个上三角矩阵
- 对某一行(列)乘以一个非零的数
- 交换两行(列)
- 将一行(列)的若干倍加到另一行(列)
解的情况有三种
- 无解,系数矩阵秩不等于增广矩阵的秩
- 有无穷多解,系数矩阵秩等于增广矩阵的秩,小于n
- 有唯一解,系数矩阵秩等于增广矩阵的秩,等于n
高斯消元算法步骤:
枚举每一列c
- 找到该列绝对值最大的一行
- 将这一行换到最上面
- 将该行第一个数变成1
- 将下面所有行的当前列消成0
- 固定该行
代码模板
// a[N][N]是增广矩阵
int gauss()
{
int c, r;
for (c = 0, r = 0; c < n; c ++ )
{
int t = r;
for (int i = r; i < n; i ++ ) // 找到绝对值最大的行
if (fabs(a[i][c]) > fabs(a[t][c]))
t = i;
if (fabs(a[t][c]) < eps) continue;
for (int i = c; i <= n; i ++ ) swap(a[t][i], a[r][i]); // 将绝对值最大的行换到最顶端
for (int i = n; i >= c; i -- ) a[r][i] /= a[r][c]; // 将当前行的首位变成1
for (int i = r + 1; i < n; i ++ ) // 用当前行将下面所有的列消成0
if (fabs(a[i][c]) > eps)
for (int j = n; j >= c; j -- )
a[i][j] -= a[r][j] * a[i][c];
r ++ ;
}
if (r < n)
{
for (int i = r; i < n; i ++ )
if (fabs(a[i][n]) > eps)
return 2; // 无解
return 1; // 有无穷多组解
}
for (int i = n - 1; i >= 0; i -- )
for (int j = i + 1; j < n; j ++ )
a[i][n] -= a[i][j] * a[j][n];
return 0; // 有唯一解
}
求组合数
从a个元素中选择b个,有多少种取法\(C_{a}^{b} = \frac{a\times(a-1)\times\dots\times(a-b+1)}{1\times2\times3\times\dots\times b} =\frac{a!}{b!\times(a-b)!}\)
求解方法
-
递推式\(C_{a}^{b} = C_{a-1}^{b} + C_{a-1}^{b-1}\),其实是dp,数据范围\(10^5\)组询问,\(1 ≤ b ≤ a ≤ 2000\),O(\(N^2\))
证明,从a个元素中分出一个元素,如果要选的b个元素包含这个元素,那么就是从剩下的a-1个元素中选b-1个,即\(C_{a-1}^{b-1}\),如果不包含这个元素,就是从a-1个元素中选择b个,即\(C_{a-1}^{b}\),综合两种情况就是\(C_{a}^{b} = C_{a-1}^{b} + C_{a-1}^{b-1}\)
代码模板:
// c[a][b] 表示从a个苹果中选b个的方案数 for (int i = 0; i < N; i ++ ) for (int j = 0; j <= i; j ++ ) if (!j) c[i][j] = 1; else c[i][j] = (c[i - 1][j] + c[i - 1][j - 1]) % mod; -
预处理逆元,数据范围\(10^4\)组询问,\(1 ≤ b ≤ a ≤ 10^5\),预处理范围内所有数的阶乘%MOD的值和阶乘的逆元%MOD的值,然后带入\(C_{a}^{b} =\frac{a!}{b!\times(a-b)!}\),求解,O(\(NlogN\))
代码模板
首先预处理出所有阶乘取模的余数fact[N],以及所有阶乘取模的逆元infact[N] 如果取模的数是质数,可以用费马小定理求逆元 int qmi(int a, int k, int p) // 快速幂模板 { int res = 1; while (k) { if (k & 1) res = (LL)res * a % p; a = (LL)a * a % p; k >>= 1; } return res; } // 预处理阶乘的余数和阶乘逆元的余数 fact[0] = infact[0] = 1; for (int i = 1; i < N; i ++ ) { fact[i] = (LL)fact[i - 1] * i % mod; infact[i] = (LL)infact[i - 1] * qmi(i, mod - 2, mod) % mod; } -
卢卡斯定理,询问很少,但是数据范围特别大\(1≤b≤a≤10^{18}\), \(1≤p≤10^{5}\), 则\(C_{a}^{b} \equiv C_{a\ mod \ p}^{b\ mod \ p} \times C_{a/p}^{b/p} \pmod{p}\) ,O(\(logN*p*logp\))
把a和b转换为p进制表示
\(a = a_{k}p^{k}+a_{k-1}p^{k-1}+\dots+a_{0}p^{0}\)
\(b= b_{k}p^{k}+b_{k-1}p^{k-1}+\dots+b_{0}p^{0}\)
生成函数\((1+x)^{p} = C_{p}^{0}*1 + C_{p}^{1}*x^1 + C_{p}^{2}*x^2 + \dots+C_{p}^{p}*x^p \equiv 1 + x^p \pmod{p}\)
所以有\((1+x)^a = ((1+x)^{p^{0}})^{a_{0}} \times ((1+x)^{p^{1}})^{a_{1}} \times ((1+x)^{p^{2}})^{a_{2}}\times \ dots \times ((1+x)^{p^{k}})^{a_{k}} = (1+x)^{a_{0}} \times (1+x^{p^{1}})^{a_{1}} \times (1+x^{p^{2}})^{a_{2}}\times \dots \times (1+x^{p^{k}})^{a_{k}}\)
对比等式\((1+x)^a = (1+x)^{a_{0}} \times (1+x^{p^{1}})^{a_{1}} \times (1+x^{p^{2}})^{a_{2}}\times \dots \times (1+x^{p^{k}})^{a_{k}}\)左右两边\(x^{b}\)项的系数,\(C_{a}^{b} \equiv C_{a_{k}}^{b_{K}} \times C_{a_{k-1}}^{b_{k-1}} \times\dots \times C_{a_{0}}^{b_{0}}\pmod{p}\)
若p是质数,则对于任意整数 1 <= m <= n,有: C(n, m) = C(n % p, m % p) * C(n / p, m / p) (mod p) int qmi(int a, int k, int p) // 快速幂模板 { int res = 1 % p; while (k) { if (k & 1) res = (LL)res * a % p; a = (LL)a * a % p; k >>= 1; } return res; } int C(int a, int b, int p) // 通过定理求组合数C(a, b) { if (a < b) return 0; LL x = 1, y = 1; // x是分子,y是分母 for (int i = a, j = 1; j <= b; i --, j ++ ) { x = (LL)x * i % p; y = (LL) y * j % p; } return x * (LL)qmi(y, p - 2, p) % p; } int lucas(LL a, LL b, int p) { if (a < p && b < p) return C(a, b, p); return (LL)C(a % p, b % p, p) * lucas(a / p, b / p, p) % p; } -
分解质因数法求组合数
当我们需要求出组合数的真实值,而非对某个数的余数时,分解质因数的方式比较好用:
- 筛法求出范围内的所有质数
- 通过 C(a, b) = a! / b! / (a - b)! 这个公式求出每个质因子的次数。 n! 中 p的次数是 n / p + n / p^2 + n / p^3 + ...
- 用高精度乘法将所有质因子相乘
int primes[N], cnt; // 存储所有质数 int sum[N]; // 存储每个质数的次数 bool st[N]; // 存储每个数是否已被筛掉 void get_primes(int n) // 线性筛法求素数 { for (int i = 2; i <= n; i ++ ) { if (!st[i]) primes[cnt ++ ] = i; for (int j = 0; primes[j] <= n / i; j ++ ) { st[primes[j] * i] = true; if (i % primes[j] == 0) break; } } } int get(int n, int p) // 求n!中的次数 { int res = 0; while (n) { res += n / p; n /= p; } return res; } vector<int> mul(vector<int> a, int b) // 高精度乘低精度模板 { vector<int> c; int t = 0; for (int i = 0; i < a.size(); i ++ ) { t += a[i] * b; c.push_back(t % 10); t /= 10; } while (t) { c.push_back(t % 10); t /= 10; } return c; } get_primes(a); // 预处理范围内的所有质数 for (int i = 0; i < cnt; i ++ ) // 求每个质因数的次数 { int p = primes[i]; sum[i] = get(a, p) - get(b, p) - get(a - b, p); } vector<int> res; res.push_back(1); for (int i = 0; i < cnt; i ++ ) // 用高精度乘法将所有质因子相乘 for (int j = 0; j < sum[i]; j ++ ) res = mul(res, primes[i]);卡特兰数
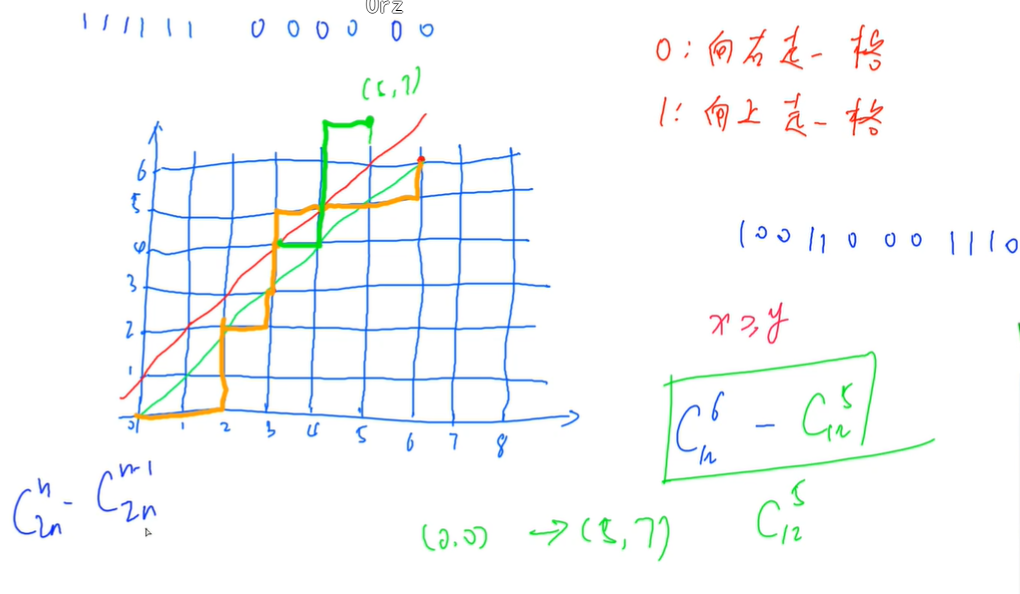
给定n个0和n个1,它们按照某种顺序排成长度为2n的序列,满足任意前缀中0的个数都不少于1的个数的序列的数量为: Cat(n) = C(2n, n) - C(2n, n-1) = C(2n, n) / (n + 1)