一个差分约束系统,是由多个形如 \(x_i-x_j\leq c\) 的不等式组成的。现在,我们要试图找出一组解,使得这些不等式都能被满足。
我们在求最短路的过程中,用到一个和上面很像的式子: \(dis_j\leq dis_i+val_i\)
所以我们把式子都化成 \(x_i\leq x_j+c\) 的形式,然后从 \(j\) 向 \(i\) 连一条边权为 \(c\) 的边。
然后我们再建一个超级源点 \(x_0\) 连向所有点,边权为 \(0\) ,代表 \(x_i \leq x_0\),\(x_0\) 的初始 \(dis\) 代表所有 \(x\) 的最小值
所以给出一组式子,我们来观察一下:
\(\begin {cases}B-A\leq x\\C-B\leq y\\C-A\leq z\end{cases}\)
我们把这张图画出来:
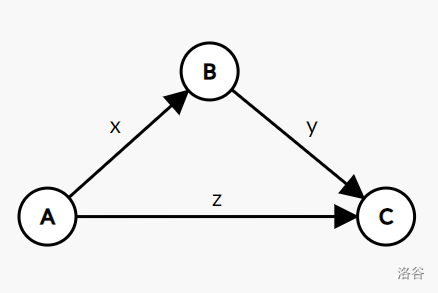
现在我们想求 \(C-A\) 的最大值,\(C-A\) 的最大值就是 \(\min\{x+y,z\}\)
然后就能发现:这就是 \(A\) 到 \(C\) 的最短路。那么如果我们从超级源点开始求到所有点的最短路,就是所有 \(x\geq x_0\) 的最大解。(啊其实说 \(x\geq x_0\) 不是很准确,应该是最小的 \(x\) 为 \(x_0\)吧 )
同理,如果我们想求,对于所有\(x\) ,\(x\geq x_0\) 的最小值,就先把式子化成 \(x_j\geq x_i -c\) 的形式,然后从 \(x_i\) 向 \(x_j\) 连一条边,边权为 \(-c\)。然后在这张图上求最长路。
怎样判断无解呢?
像这样的一组不等式是无解的:
\(\begin{cases}x_2\leq x_1 +3\\x_3\leq x_2-5\\x_1\leq x_3 -2\end{cases}\)
三个式子加起来得到 \(x_1\leq x_1-4\) 显然不成立。
然后把图画出来就能发现这是一个负环。所以判断有解的方式就是判负环(当然如果是求最长路就是判正环)
所以大多数时候用 spfa 就行了。
但是如果给出的式子是形如 \(x_i-x_j\geq c\) 的,就移一下项。如果式子是 \(x_i=x_j+c\) ,就先拆成 \(x_i\leq x_j+c\) 和 \(x_i\geq x_j+c\) 两个式子,如果是 \(x_i<x_j\) ,就化成 \(x_i\leq x_j -1\)
然后挂两个例题
[SCOI2011]糖果
如果不看数据范围,那就是板子。
但是 spfa 的最坏时间复杂度是过不了的。
然后你可以发现,如果你建出最长路的模型,边权只有 \(0\) 和 \(1\) 两种。所以我们可以先用 tarjan 缩点,如果一个强联通分量里有边权为 \(1\) 的边,因为强联通分量里所有点可以互相到达,所以一定存在正环,直接无解。所以一个强联通分量里所有的点的最短路都是相等的。这样缩点之后直接跑一次拓扑排序就行了
SP116 INTERVAL - Intervals
我们用 \(s_i\) 表示 \(0\sim i\) 中已经最少选了多少数了,那么我们有这么几个不等式:\(s_{r_i}-s_{l_i-1}\geq c_i,s_i\geq s_{i-1},s_i\leq s_{i-1}+1\)
第一个式子是题目的约束条件,第二个是表示必须保证 \(s\) 单调不降,第三个保证每个数只选一次。
然后注意到我们必须保证 \(s_{-1}=0\) ,所以不能建超级源点。直接从 \(-1\) 开始。
负下标就直接向右平移一位就行了。
[SCOI2008]天平
由 \(A+B>C+D\) 可以推出 \(A-C>D-B\) ,或者 \(A-D>C-B\)
那么就是我们要求 \(A-C\), \(D-B\) ,\(A-D\) ,\(C-B\) 的取值范围了。
我们上面说了,建边之后跑最短路就是差最大,最长路就是差最小。
那么我们分两个数组,\(mx\) 用来求最大的差值,\(mn\) 用来求最小的差值。
具体地说,如果要求 \(a_i>a_j,mx_{i,j}=2,mn_{i,j}=1\)
如果 \(a_i<a_j,mx_{i,j}=-1,mn_{i,j}=-2\)。
其实理解为当 \(a_i>a_j,a_i\leq a_j+2,a_i\geq a_j+1\) ,按照这种理解建边。
然后用 floyd 直接跑全源最短(长)路。
如果 \(A+B>C+D\) 就意味着 \(mn_{A,C}>mx_{D,B}\) 或 \(mn_{A,D} >mx_{C,B}\) ,这样才能保证一定合法。
其他两种情况也差不多。
标签:geq,边权,短路,笔记,约束,leq,差分,我们,式子 From: https://www.cnblogs.com/cc0000/p/16728155.html