fft.1
单位根的性质
\[1.w^{dk}_{dN}=w^k_N \]\[2.\frac{1}{\omega_k}=\omega_k^{-1}=e^{-\frac{2\pi i}{k}}=\cos\left(\frac{2\pi}{k}\right)+i\cdot \sin\left(-\frac{2\pi}{k}\right) \]递归求解 \(F[\) \(]\) = \(1\) \(2\) \(3\) \(4\) \(5\) \(6\) .....这里指的是项数或者直接说是数组的下标

递归到最后一项就是值了 所以我们倍增求解
fft.2
1.复数怎么求
\[\omega_n^{2} = (\omega_n^{1})^2 \]\[\omega_{2n}^{2k} = \omega_n^k \]\[\omega_{n}^{k+n/2} = -\omega_{n}^k \]->感性理解下 很容易去推
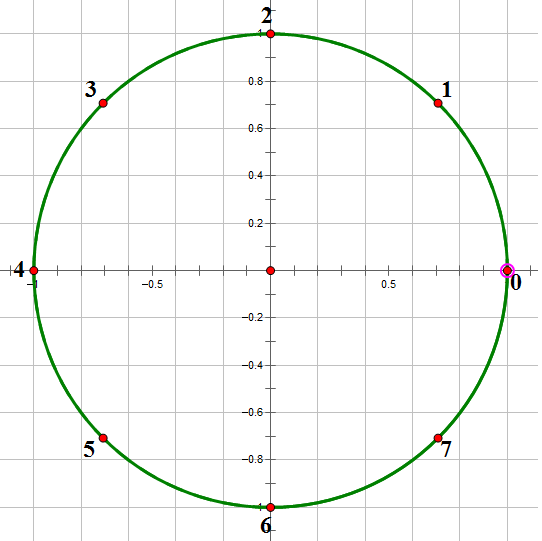
2. 原理解释
好的,我可以给您一个 FFT 的原理解释。
标签:frac,原根,FFT,笔记,学习,mod,omega,2k From: https://www.cnblogs.com/mhunice/p/fft_mhunice.html