题解 P5597【【XR-4】复读】

一道好题！挺对我脑回路的，于是秒掉了，来写个题解。

下文称执行一遍指令的过程为一个周期。例如指令是 LRU，那么 LRULRULRULRU 共执行了四个周期。

看到平方的数据范围，不难想到枚举第一个周期的终点。作为一台优秀的复读机，我们知道每个周期在树上发生的相对位移是相同的。

例如，如下的一棵树，如果第一周期从 \(1\) 移动到 \(4\)，那么第二周期一定从 \(4\) 移动到 \(16\)：

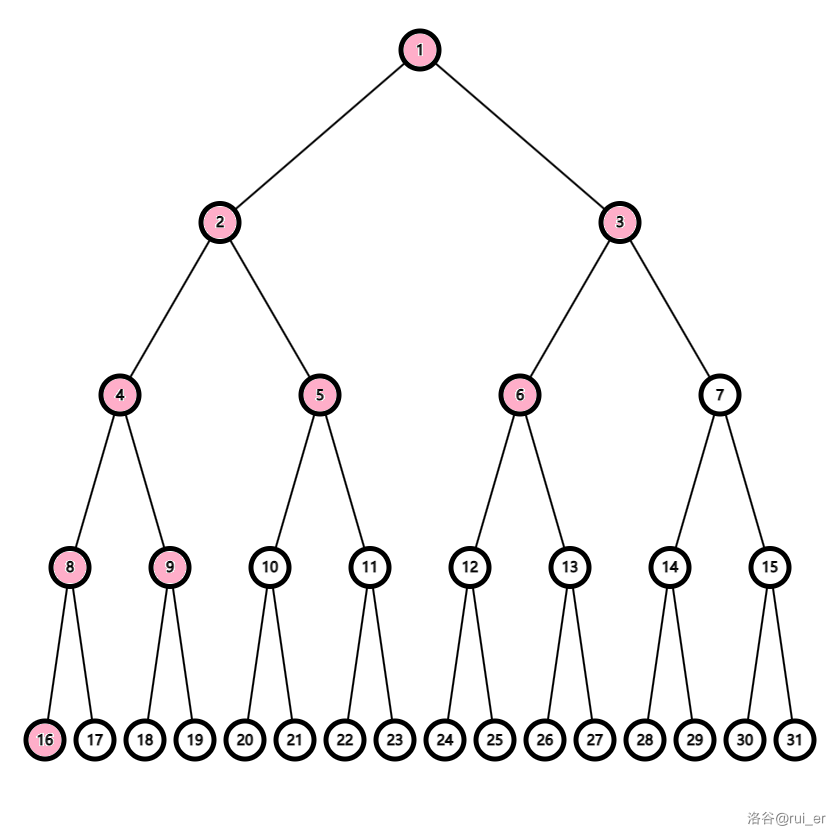
同时，因为在根节点的 U 操作非法，假设一个周期从 \(u\) 开始，那么途中一定一直在 \(u\) 的子树内，不可能到 \(u\) 上面。

依然假设第一周期从 \(1\) 移动到 \(4\)，那么根据这一点，我们第一周期中必须把所有在 \(1\) 子树内但不在 \(4\) 子树内的节点访问一遍，也就是 \(1,2,3,5,6\)，并最终停在 \(4\)。同理，第二周期必须把 \(4,8,9\) 访问一遍并停在 \(16\)，第三周期必须把 \(16\) 访问一遍。

我们把 \((1,2,3,4,5,6),(4,8,9,16),(16)\) 三棵子树取一个并（如下图所示），其中每个周期要从绿色的点出发，经过所有粉色的点，最终到达蓝色的点。

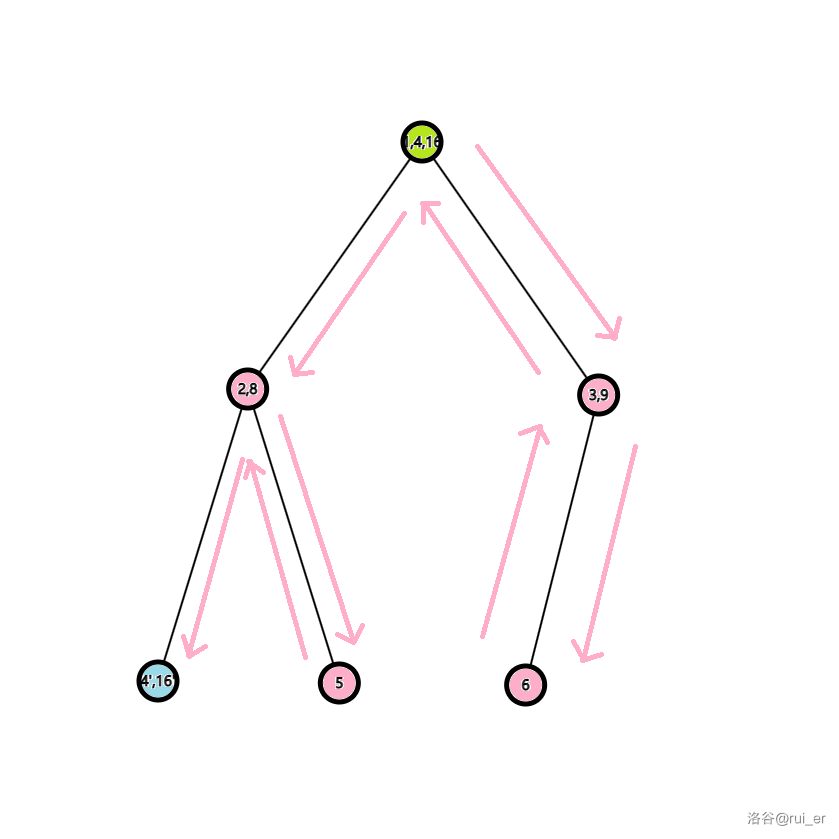
显而易见地，最少需要的指令数为 \(2(n-1)-\Delta d\)，其中 \(n\) 为这棵树中的点数，\(\Delta d\) 是起点和终点之间的边数。上图给出了一种构造，即 RLUULRUL。

枚举第一个周期的终点，然后求出所有这样的子树的并，最后根据上面公式统计最优解即可。

时间复杂度 \(\mathcal O(n^2)\)。

//By: OIer rui_er
#include <bits/stdc++.h>
#define rep(x,y,z) for(int x=(y);x<=(z);x++)
#define per(x,y,z) for(int x=(y);x>=(z);x--)
#define debug(format...) fprintf(stderr, format)
#define fileIO(s) do{freopen(s".in","r",stdin);freopen(s".out","w",stdout);}while(false)
using namespace std;
typedef long long ll;

mt19937 rnd(std::chrono::duration_cast<std::chrono::nanoseconds>(std::chrono::system_clock::now().time_since_epoch()).count());
int randint(int L, int R) {
    uniform_int_distribution<int> dist(L, R);
    return dist(rnd);
}

template<typename T> void chkmin(T& x, T y) {if(x > y) x = y;}
template<typename T> void chkmax(T& x, T y) {if(x < y) x = y;}

const int N = 2048;

struct BinaryTree {
    int lc[N], rc[N], sz, rt;
    BinaryTree() {
        memset(lc, 0, sizeof(lc));
        memset(rc, 0, sizeof(rc));
        sz = rt = 0;
    }
    int read() {
        int c = getchar() ^ 48, u = ++sz;
        if(c & 1) lc[u] = read();
        if(c & 2) rc[u] = read();
        return u;
    }
}T, TU; // original tree; the union of trees

void dfs_union(int u, int v, int root, int key) { // calculate the union
    if(u == root || v == key) {
        if(!key) key = v;
        v = TU.rt;
    }
    if(T.lc[u]) {
        if(!TU.lc[v]) TU.lc[v] = ++TU.sz;
        dfs_union(T.lc[u], TU.lc[v], root, key);
    }
    if(T.rc[u]) {
        if(!TU.rc[v]) TU.rc[v] = ++TU.sz;
        dfs_union(T.rc[u], TU.rc[v], root, key);
    }
}

int dfs_enum(int u, int d) { // enumerate the destination of round #1 moving
    TU = BinaryTree();
    TU.sz = TU.rt = 1;
    dfs_union(T.rt, TU.rt, u, 0);
    int ans = (TU.sz - 1) * 2 - d;
    if(T.lc[u]) chkmin(ans, dfs_enum(T.lc[u], d+1));
    if(T.rc[u]) chkmin(ans, dfs_enum(T.rc[u], d+1));
    return ans;
}

int main() {
    T.rt = T.read();
    printf("%d\n", dfs_enum(T.rt, 0));
    return 0;
}