前言
非常好的数据结构优化题。
思路
对于第 \(x\) 次询问,答案为 \(\dfrac{\sum\limits_{i=1}^x\sum\limits_{j=1}^x \max(a_i, a_j)}{x^2}\)。分母显然可以用逆元求,所以看上面那一坨。
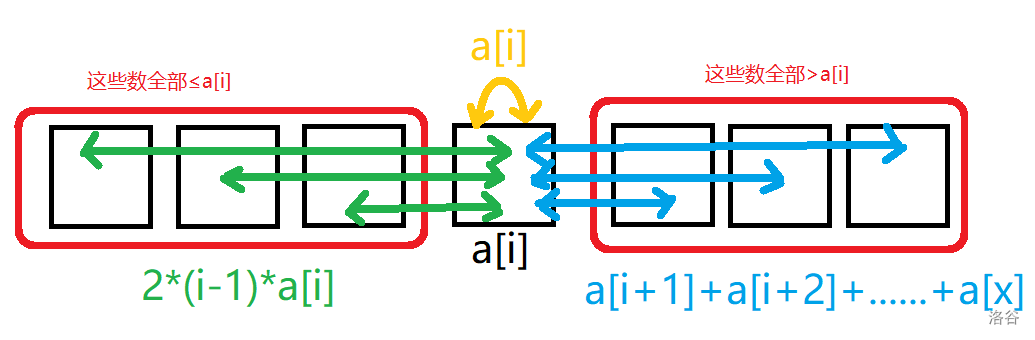
看上面这幅图就比较显然了,我们只需要在线维护数据结构,支持:
- 求出有多少个 \(a_j \le a_i\)。
- 求出所有满足 \(a_j > a_i\) 的 \(\sum a_j\)。
- 加入一个元素 \(a_i\)。
注意到 \(\forall a_i \le 2 \times 10^5\),所以直接上权值树状数组即可,一个维护数量,一个维护总和。
代码
#include <iostream>
#include <cstdio>
using namespace std;
const int N = 2e5 + 5, mod = 998244353;
int inv(int x, int y = mod - 2)
{
int ans = 1;
while (y)
{
if (y & 1) ans = 1ll * ans * x % mod;
x = 1ll * x * x % mod;
y >>= 1;
}
return ans;
}
struct BIT { //权值树状数组
int idx[N];
int lowbit(int x) {return x & -x;}
void update(int i, int k) {for (; i < N; i += lowbit(i)) (idx[i] += k) %= mod;}
int query(int i) {int ans = 0; for (; i; i -= lowbit(i)) ans = (ans + idx[i]) % mod; return ans;}
} cnt, sum;
int main()
{
int n, total = 0, ans = 0;
scanf("%d", &n);
for (int i = 1; i <= n; i++)
{
int a;
scanf("%d", &a);
ans += (2ll * cnt.query(a) + 1) * a % mod; ans %= mod;
ans += (2ll *(total - sum.query(a)) % mod + mod) % mod; ans %= mod;
printf("%d\n", 1ll * ans * inv(1ll * i * i % mod) % mod);
total = (total + a) % mod;
cnt.update(a, 1), sum.update(a, a);
}
return 0;
}
希望能帮助到大家!
标签:return,int,题解,sum,ABC261F,ans,lowbit,mod From: https://www.cnblogs.com/liangbowen/p/17435683.html