样例输入: 样例输出:题面


(图是偷来的)。\(1\le n,m\le2*10^5,1\le d_i\le10^8\)。5 6
4 5
3 6
1 2
8 7
1 1 5 1
2 2 3
2 1 5
1 2 5 3
2 2 4
2 3 5
0
5
3
9
广义二叉树有这样一种普遍的处理方法:
定义 \(is_a\) 表示 \(a\) 是否是它父亲的左儿子。(根的值为 \(-1\))
定义 \(ff_a\) 表示 \(a\)的真祖先中第一个和 \(a\) \(is\) 值不同的祖先的兄弟节点。
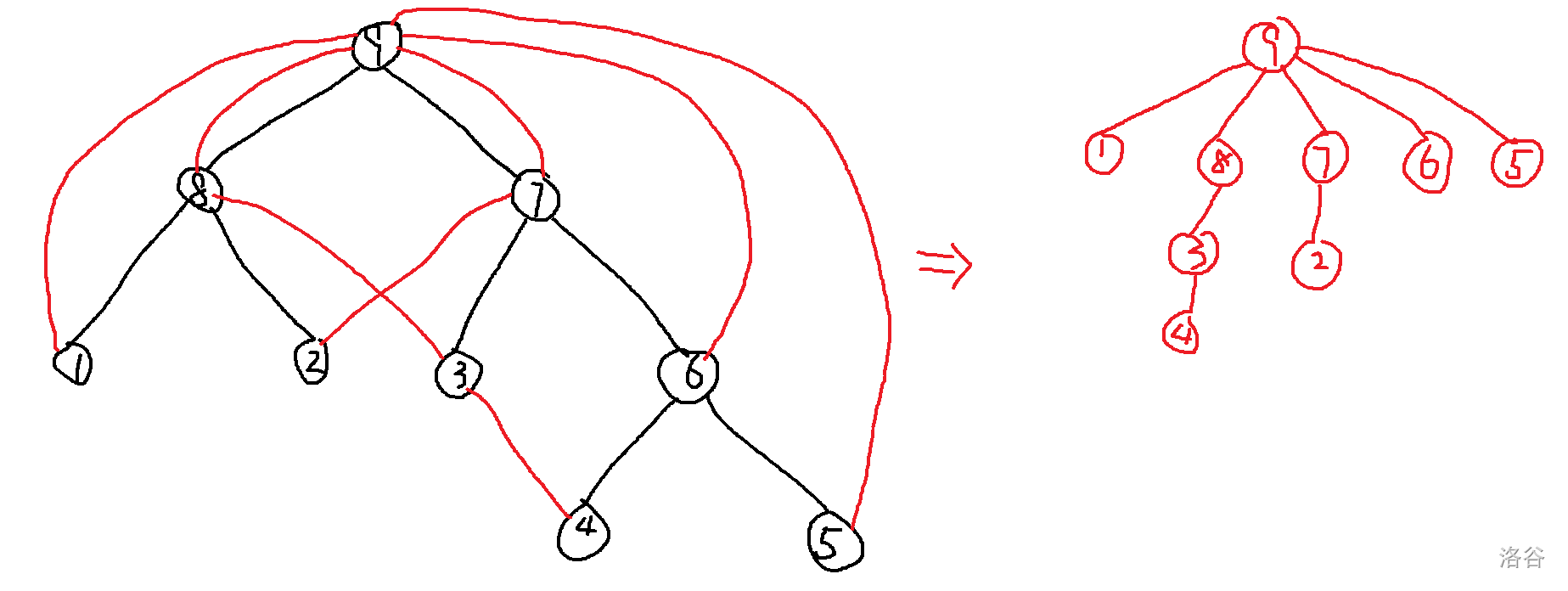
连接 \(a,ff_a\) ,显然仍能得到一颗以原来根为根的树。不理解可以见下图。
先对于左儿子求它的 \(ff\) ,右儿子同理。
开个栈,每次先将当前点的左儿子与栈顶元素相连,然后将当前点左儿子压入栈,遍历当前点右子树,再将左儿子弹出栈,再遍历左子树,如此得到。可以在 \(\texttt{dfs}\) 时直接开一个变量表示栈顶,省掉栈。
void Do(int th,int x)
{
if(!S[th][0]) return;
add(S[th][o],x);Do(S[th][o^1],S[th][o]);Do(S[th][o],x);
}//o 左边0右边1,可以通过代码理解一下上面文字
下面 \(\text{lca}\) 表示原树的 \(\text{lca}\)。\(fa\) 表示现在树的父亲,操作包括加和查两种。
考虑 \([l,r]\) 区间在原树包含的节点,它一定可以在现在的树分成两条链,一条所有点都在原来 \(\text{lca}\) 的左边,另一条反之。
下面只考虑左链,右链同理。
先对于节点 \(l\) ,我们找到 \(l\) 在原树上一直向右上跳的最远位置(设其为 \(u\))
如果这个点在原树上的深度比 \(\text{lca}\) 深(即没跳过 \(\text{lca}\) ),
那么从 \(u\) 开始在现树上往上跳,发现一定能跳到 \(\text{lca}\) 的右儿子(通过连边时的情况可以证明),在跳的时候操作每一个点。但是右儿子又不会和左边的操作相关,于是最后要减掉右儿子的操作,那么左边的所有点都不重不漏得操作完了。
比如上面那幅样例的图 \(\text{lca}=9,l=2\),则把 \(2,7\) 操作,\(7\) 取消操作。
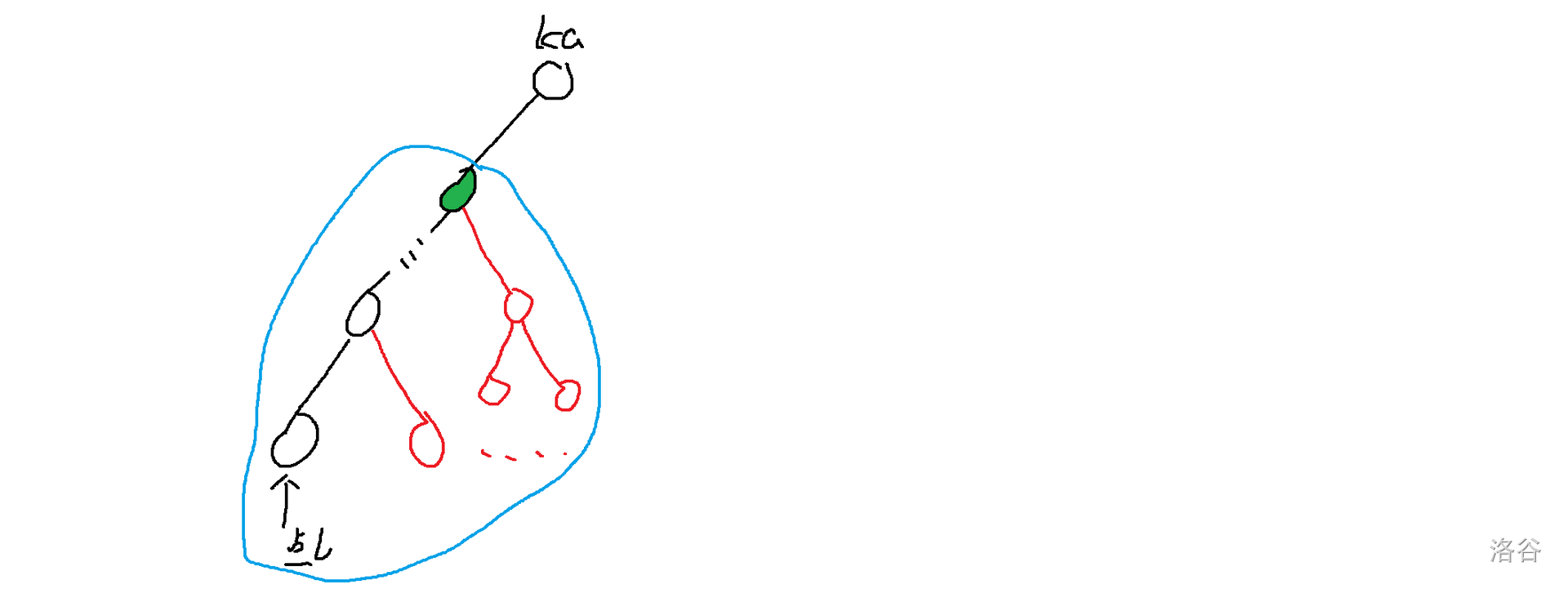
如果跳过 \(\text{lca}\),那么必定是这种情况:
那么左边就只会操作绿色的点,即 \(\text{lca}\) 的左儿子。
有一个特殊情况,左右边都是上面那种特殊情况,则只会操作 \(\text{lca}\)。
最后说如何求点 \(u\) , 如果 \(is_l=1\),则 \(u=l\),否则 \(u=fa_l\) 的在原树上的兄弟.
现在就把一次操作转化为现树的一条链操作,树剖+线段树即可。
$\texttt{code}$
#include<bits/stdc++.h>
#define LL long long
#define fr(x) freopen(#x".in","r",stdin);freopen(#x".out","w",stdout);
using namespace std;
inline int rd()
{
int x=0,zf=1;
char ch=getchar();
while(ch<'0'||ch>'9') (ch=='-')and(zf=-1),ch=getchar();
while(ch>='0'&&ch<='9') x=x*10+ch-'0',ch=getchar();
return x*zf;
}
inline void wr(LL x)
{
if(x==0) return putchar('0'),putchar('\n'),void();
if(x<0) x=-x,putchar('-');
short num[35],len=0;
while(x) num[++len]=x%10,x/=10;
for(int i=len;i>=1;i--) putchar(num[i]+'0');
putchar('\n');
}
const int N=4e5+5;
int n,m,RT,tot,head[N],D[N],FA[N][25],S[N][2],br[N];
int fa[N],d[N],siz[N],ms[N],tp[N],id[N];LL cnt[N],s[N];
bool v[N];
struct edge{int to,nex;}e[N<<1];
inline void add(int u,int v)
{
e[++tot]={v,head[u]};head[u]=tot;
e[++tot]={u,head[v]};head[v]=tot;
}
namespace DO
{
int o;
void dfs(int th,int fa)
{
FA[th][0]=fa;D[th]=D[fa]+1;
for(int i=1;i<=20;i++) FA[th][i]=FA[FA[th][i-1]][i-1];
if(S[th][0]) dfs(S[th][0],th),dfs(S[th][1],th),cnt[th]=cnt[S[th][0]]+cnt[S[th][1]];
else cnt[th]=1;
}
void Do(int th,int x)
{
if(!S[th][0]) return;
add(S[th][o],x);Do(S[th][o^1],S[th][o]);Do(S[th][o],x);
}
void dfs1(int th,int fa)
{
::fa[th]=fa;d[th]=d[fa]+1;siz[th]=1;
for(int i=head[th];i;i=e[i].nex)
{
int to=e[i].to;
if(to==fa) continue;dfs1(to,th);siz[th]+=siz[to];
if(siz[ms[th]]<siz[to]) ms[th]=to;
}
}
void dfs2(int th,int TP)
{
id[th]=++tot;s[tot]=cnt[th];tp[th]=TP;if(ms[th]) dfs2(ms[th],TP);
for(int i=head[th];i;i=e[i].nex)
{
int to=e[i].to;
if(to==fa[th]||to==ms[th]) continue;dfs2(to,to);
}
}
inline void init()
{
dfs(RT,0);tot=0;o=0;Do(RT,RT);o=1;Do(RT,RT);
tot=0;dfs1(RT,0);dfs2(RT,RT);
for(int i=1;i<2*n;i++) s[i]+=s[i-1];
}
}
namespace SigT
{
LL a[N<<2],lt[N<<2];
inline void pushdown(int l,int r,int wz)
{
int mid=(l+r)>>1;LL x=lt[wz];
lt[wz<<1]+=x;lt[wz<<1|1]+=x;lt[wz]=0;
a[wz<<1]+=1ll*(s[mid]-s[l-1])*x;a[wz<<1|1]+=1ll*(s[r]-s[mid])*x;
}
void add(int l,int r,int wz,int L,int R,int x)
{
if(L<=l&&r<=R) return a[wz]+=1ll*(s[r]-s[l-1])*x,lt[wz]+=x,void();
int mid=(l+r)>>1;pushdown(l,r,wz);
if(L<=mid) add(l,mid,wz<<1,L,R,x);
if(mid<R) add(mid+1,r,wz<<1|1,L,R,x);
a[wz]=a[wz<<1]+a[wz<<1|1];
}
LL ask(int l,int r,int wz,int L,int R)
{
if(L<=l&&r<=R) return a[wz];
int mid=(l+r)>>1;pushdown(l,r,wz);LL ans=0;
if(L<=mid) ans+=ask(l,mid,wz<<1,L,R);
if(mid<R) ans+=ask(mid+1,r,wz<<1|1,L,R);
return ans;
}
}
inline int lca(int x,int y)
{
if(D[x]<D[y]) swap(x,y);
int t=D[x]-D[y];
for(int i=0;t;t>>=1,i++) if(t&1) x=FA[x][i];
if(x==y) return x;
for(int i=20;i>=0;i--) if(FA[x][i]!=FA[y][i]) x=FA[x][i],y=FA[y][i];
return FA[x][0];
}
#define pd(x) x==S[FA[x][0]][1]
inline void ad(int W,int L,int x,int o)
{
int t=S[L][o^1];
if(D[W]<=D[L]) return SigT::add(1,2*n-1,1,id[S[L][o]],id[S[L][o]],x),void();
while(tp[t]!=tp[W])
{
int X=id[tp[W]],Y=id[W];
SigT::add(1,2*n-1,1,X,Y,x);W=fa[tp[W]];
}
SigT::add(1,2*n-1,1,id[t],id[W],x);
SigT::add(1,2*n-1,1,id[S[L][o^1]],id[S[L][o^1]],-x);
}
inline void ADD(int l,int r,int x)
{
int L=lca(l,r);(pd(l)^1)&&(l=br[fa[l]]);(pd(r))&&(r=br[fa[r]]);
if(D[l]<=D[L]&&D[r]<=D[L]) return SigT::add(1,2*n-1,1,id[L],id[L],x),void();
ad(l,L,x,0);ad(r,L,x,1);
}
inline LL qu(int W,int L,int o)
{
int t=S[L][o^1];LL ans=0;
if(D[W]<=D[L]) return SigT::ask(1,2*n-1,1,id[S[L][o]],id[S[L][o]]);
while(tp[t]!=tp[W])
{
int X=id[tp[W]],Y=id[W];
ans+=SigT::ask(1,2*n-1,1,X,Y);W=fa[tp[W]];
}
ans+=SigT::ask(1,2*n-1,1,id[t],id[W]);
ans-=SigT::ask(1,2*n-1,1,id[S[L][o^1]],id[S[L][o^1]]);
return ans;
}
inline LL query(int l,int r)
{
int L=lca(l,r);(pd(l)^1)&&(l=br[fa[l]]);(pd(r))&&(r=br[fa[r]]);LL ans=0;
if(D[l]<=D[L]&&D[r]<=D[L]) return SigT::ask(1,2*n-1,1,id[L],id[L]);
ans+=qu(l,L,0);ans+=qu(r,L,1);
return ans;
}
int main()
{
n=rd();m=rd();int op,l,r,x;
for(int i=1,x,y;i<n;i++) S[n+i][0]=x=rd(),S[n+i][1]=y=rd(),v[x]=v[y]=1,br[x]=y,br[y]=x;
for(int i=1;i<2*n;i++) if(!v[i]){RT=i;break;}DO::init();
while(m--)
{
op=rd();l=rd();r=rd();
if(op==1) x=rd(),ADD(l,r,x);
else wr(query(l,r));
}
return 0;
}