2022-2023 春学期 矩阵与数值分析 C4 逐次逼近法
C4 逐次逼近法
4.1 解线性方程组的迭代法
简单迭代法迭代格式
可将线性方程组变形
\[Ax=b \Leftrightarrow x=Bx+f \]其中 B 为迭代矩阵,且
\[B\in R^{n\times n},f\in R^n,x\in R^n \]迭代法:称使用
\[x^{(k+1)}=Bx^{k}+f\;(k=0,1,2,\cdots) \]求解的方法为迭代法,也称迭代过程或迭代格式.
迭代法收敛、发散:如果对任意 \(x^{(0)}\) ,都有 \(\lim\limits_{k\to\infty}x^{(k)}=x^*\)。即
\[\lim\limits_{k\to\infty}x_i^{(k)}=x_i^*,\;i=1,2,\cdots,n \]称该迭代法收敛,否则称迭代法发散。
Jacobi,Gauss-seidel 迭代法等
简单迭代法-方程组变形
线性方程组:
\[\left\{ \begin{array}{c} a_{11}x_1+a_{12}x_2+\cdots+a_{1n}x_n=b_1\\ \vdots\\ a_{n1}x_1+a_{n2}x_2+\cdots+a_{nn}x_n=b_n \end{array} \right. \]等价方程组:\(a_{ii}\neq0\)
\[\left\{ \begin{array}{l} x_1=\frac{1}{a_{11}}(b_1-a_{12}x_2-\cdots-a_{1n}x_n)\\ \qquad\qquad\qquad\qquad\qquad\vdots\\ x_i=\frac{1}{a_{ii}}(b_i-a_{i1}x_1-\cdots-a_{ii-1}x_{i-1}-a_{ii+1}x_{i+1}-\cdots-a_{in}x_n)\\ \qquad\qquad\qquad\qquad\qquad\vdots\\ x_n=\frac{1}{a_{nn}}(b_a-a_{n1}x_1-\cdots-a_{nn-1}x_{n-1}) \end{array} \right. \]Jacobi 迭代法:
\[x_i^{(k+1)}=\frac{1}{a_{ii}}(b_i-\sum\limits^{i-1}_{j=1}a_{ij}x_j^{(k)}-\sum\limits^n_{j=i+1}a_{ij}x_j^{(k)})\;(i=1,2,\cdots,n) \]在 Jacobi 迭代过程中,对已经算出来的信息未加以充分利用,比如在计算 \(x^{k+1}_2\) 时 \(x^{k+1}_1\) 已经算出,可是使用 Seidel 技巧加以改进,得到 Gauss-Seidel 迭代法:
\[x_i^{(k+1)}=\frac{1}{a_{ii}}(b_i-\sum\limits^{i-1}_{j=1}a_{ij}x_j^{(k+1)}-\sum\limits^n_{j=i+1}a_{ij}x_j^{(k)})\;(i=1,2,\cdots,n) \]矩阵分裂:可以将系数矩阵 A 分裂为 A=D-L-U 的形式,具体如下所示:
\[A=D-L-U\\ A= \begin{pmatrix} a_{1,1}&a_{1,2}&\cdots&a_{i,j}&\cdots&a_{1,n}\\ a_{2,1}&a_{2,2}&\cdots&\cdots&\cdots&a_{2,n}\\ \vdots&\ddots&\ddots&\vdots&\vdots&\vdots \\ a_{i,1}&\cdots&a_{i,j-1}&a_{i,j}&\cdots&a_{i,n} \\ \vdots&&\vdots&\ddots&\ddots&\vdots \\ a_{n,1}&\cdots&a_{n,j-1}&\cdots&a_{n,n-1}&a_{n,n} \end{pmatrix}\\ D=\mathrm{diag(a_{1,1},a_{2,2},\cdots,a_{n,n})}\\ L= \begin{pmatrix} 0&&&&&0\\ -a_{2,1}&0\\ \vdots&\ddots&\ddots\\ -a_{j,1}&\cdots&-a_{j,j-1}&0\\ \vdots&&\vdots&\ddots&\ddots\\ -a_{n,1}&\cdots&-a_{n,j-1}&\cdots&-a_{n,n-1}&0 \end{pmatrix}\\ U= \begin{pmatrix} 0&-a_{1,2}&\cdots&-a_{1,j}&\cdots&-a_{1,n}\\ &\ddots&\ddots&\vdots&&\vdots\\ &&0&-a_{j-1,j}&\cdots&-a_{j-1,n}\\ &&&\ddots&\ddots&\vdots\\ &&&&0&-a_{n-1,n}\\ 0&&&&&0\\ \end{pmatrix}\\ \]Jacobi、Gauss-Seidel 迭代法矩阵格式
由 A=D-L-U,得 Dx=(L+U)x+b 从而有:
\[x=D^{-1}(L+U)x+D^{-1}b \]则 Jacobi 迭代法可写成:
\[x^{(k+1)}=D^{-1}(L+U)x^{(k)}+D^{-1}b;\;k=0,1,2,\cdots \]由 A=D-L-U,得 (D-L)x=Ux+b 从而
\[x=(D-L)^{-1}Ux+(D-L)^{-1}b \]则 Gauss-Seidel 迭代法可以写成:
\[x^{(k+1)}=(D-L)^{-1}Ux^{(k)}+(D-L)^{-1}b;\;k=0,1,2,\cdots \]并不是对任何情况,G-S 迭代都比 Jacobi 迭代收敛速度快
例题
1


*迭代改善法(应该不会考)


迭代法的收敛性
迭代法收敛性定理(谱半径):迭代法 \(x^{(k+1)}=Bx^{(k)}+f\) 对任意 \(x^{(0)}\) 和 \(f\) 均收敛的充要条件为:
\[\rho(B)<1 \]迭代法收敛性定理(范数):若迭代矩阵任意范数 \(||B||<1\),则迭代法收敛,且有
\[||x^{(k)}-x^*||\leq\frac{||B||^k}{1-||B||}||x^{(1)}-x^{(0)}|| \]定理: \(\lim\limits_{k\to\infty}\epsilon^{(k)}=0\)(即迭代收敛 \(x_i^{(k)}\to x_i^*,i=1,2,\cdots,n\))的充分必要条件是 \(\lim\limits_{k\to\infty}B^k=0_{n\times n}\Leftrightarrow \rho(B)<1\)
迭代法收敛性-特殊线性方程组
针对某些特殊方程组,从方程组本身就可以判定其收敛性,不必求迭代矩阵的特征值或范数
-
严格(不可约)对角占优矩阵
-
定义:如果矩阵 \(A=(a_{ij})_{n\times n}\) 的元素满足不等式 \(|a_{ii}|\geq\sum\limits_{j=1,j!=i}^n|a_{ij}|,\;(i=1,2,\cdots,n)\),则称 A 为对角占优阵;如果所有严格不等式(即不等式不取等号)均成立,称 A 为严格对角占优矩阵。
-
定理:严格对角占优阵 A 为非奇异矩阵,即 \(\det(A)\neq0\)
-
定理:若线性方程组 Ax=b 中的 A 为严格对角占优矩阵,则 Jacobi 法和 Gauss-Seidel 法均收敛。
-
-
对称正定矩阵
若 A 为对称正定矩阵:
- 若 2D-A 为正定矩阵,则 Jacobi 迭代法收敛
- Gauss-Seidel 迭代法收敛
例题

4.2 非线性方程迭代解法
相关的概念
根、零点:对于非线性方程 f(x)=0 ,若数 a 满足 f(a)=0,则称 a 为方程的根,或称函数 f(x) 的零点
有根区间:如果 f(x)=0 在区间 [a,b] 上仅有一个根,则称 [a,b] 为方程的单根区间;若方程在 [a,b] 上有多个根,则称 [a,b] 为方程的多根区间。方程的单根区间和多根区间统称为方程的有根区间;这里主要研究方程在单根区间上的求解方法。
将方程 f(x)=0 化为一个与它同解的方程 \(x=\varphi(x)\),其中 \(\varphi(x)\) 为 x 的连续函数;就代入初值可以进行迭代求解
简单迭代法:称 \(x_{k+1}=\varphi(x)\) 为求解非线性方程的简单迭代法,也称迭代法或迭代过程或迭代格,\(\varphi(x)\) 称为迭代函数,\(x_k\) 称第 k 步的迭代之或简称迭代值。
迭代法收敛:如果由迭代格式缠身的数列收敛,即 \(\lim\limits_{k\to\infty}x_k=a\),则称迭代法收敛,否则称迭代法发散;若迭代法收敛于 a,则有 \(a=\varphi(a)\Leftrightarrow f(a)\equiv a\),则 a 就是方程的根。
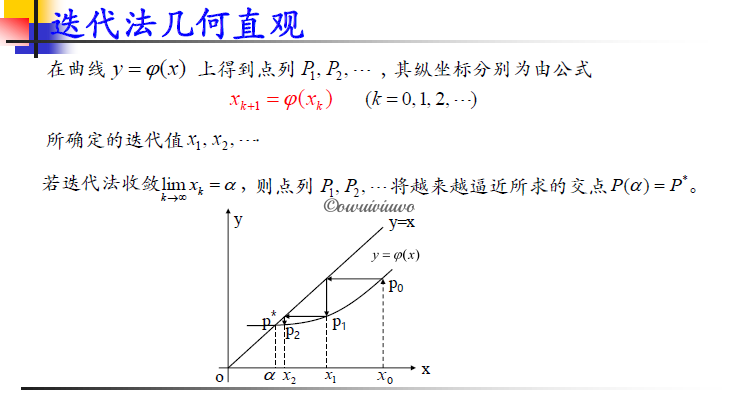
迭代法收敛
几何表示
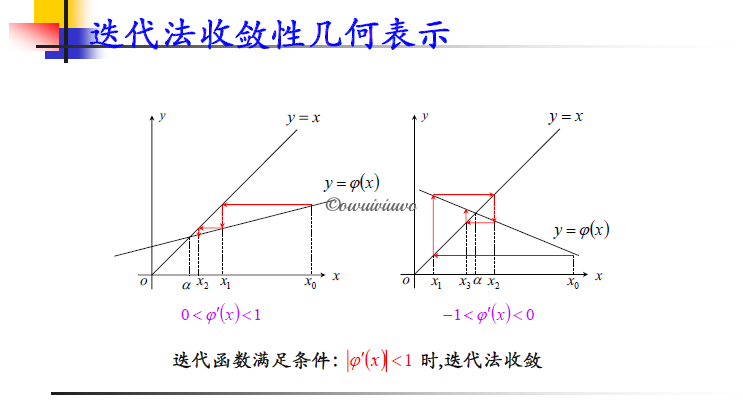
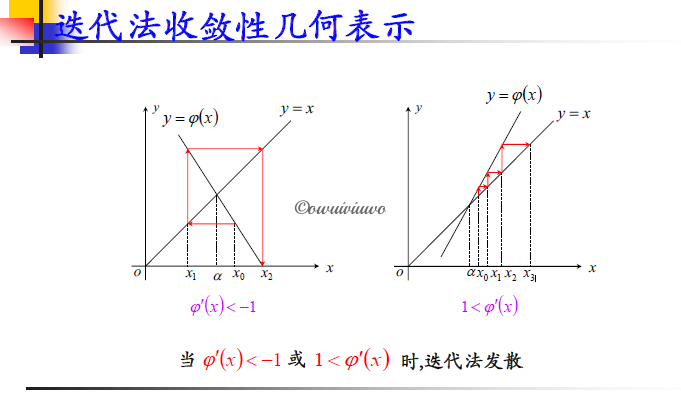
收敛性定理:设迭代函数 \(\varphi(x)\) 满足
- 当 \(x\in[a,b]\) 时,\(a\leq\varphi(x)\leq b\)
- 存在正数 \(0<L<1\),对任意 \(x\in[a,b]\) 均有 \(|\varphi'(x)|\leq L\)(难以验证)
则 \(x=\varphi(x)\) 在 \([a,b]\) 内存在唯一根 \(a\),且对任意初始值 \(x_0\in[a,b]\) ,迭代法
\[x_{k+1}=\varphi(x_k)\;(k=0,1,2,\cdots) \]收敛于 \(a\),且
\[|x_k-a|\leq\frac{L}{1-L}|x_k-x_{k-1}|\leq\frac{L^k}{1-L}|x_1-x_0| \]L 较小,相邻两次计算值的偏差 \(|x_k-x_{k-1}|\leq\delta\) (事先给定的精度),迭代过程就可以终止,\(x_k\) 就可以作为 a 的近似值
L 的大小可作出估计时,估计所需要的迭代次数
\[|x_k-a|\leq\frac{L^k}{1-L}|x_1-x_0|<\delta\rightarrow k\geq \log_L\frac{\delta(1-L)}{|x_1-x_0|} \]使用迭代法时往往在根 a 的附近进行,假定 \(\varphi'(x)\) 在 a 的附近连续且满足 \(|\varphi'(a)|<1\),则一定存在 a 的某个领域 \(S:|x-a|\leq\delta\) ,\(\varphi(x)\) 在 S 上满足收敛性定理中的条件,所以在 S 中任取初始值 \(x_0\),迭代格式
\[x_k=\varphi(x_{k-1}) \]收敛于方程的根 a,即 \(f(a)\equiv0\),称此收敛为局部收敛。
误差估计式:
\[|x_k-a|\leq\frac{L^k}{1-L}|x_1-x_0| \]中 L 或 \(|\varphi'(x)|\) 在 \([a,b]\) 上的值越小,迭代的收敛速度就越快。L < 1 且接近于 1 时,迭代法虽然收敛,但收敛速度很慢。
为了使收敛速度有定量的判断, 特介绍收敛速度的阶的概念,作为判断迭代法收敛速度的重要标准。
设迭代格式 \(x_{k+1}=\varphi(x_k)\),当 \(k\to\infty\) 时,\(x_{k+1}\to a\) 记 \(e_k=x_k-a\)
迭代法收敛阶:若存在实数 \(p\geq1\) 和 \(c>1\) 满足
\[\lim\limits_{k\to\infty}\frac{|e_{k+1}|}{|e_k|^p}=c \]则称迭代法是 p 阶收敛,当 p=1 时,称线性收敛,当 p>1 时称超线性收敛,当 p=2 时称平方收敛。
显然:
- 收敛阶越大迭代法的收敛速度也越快
- 收敛阶难以直接确定,课采用一些其他方法来确定收敛阶(Taylor 展开式)

收敛阶判定定理
p 阶收敛:如果 \(x=\varphi(x)\) 中的迭代函数 \(\varphi(x)\) 在根 a 附近满足:
-
\(\varphi(x)\) 存在 p 阶导数且连续
- \[ \varphi'(a)=\varphi''(a)=\cdots=\varphi^{(p-1)}(a)=0,\;\varphi^{(p)}(a)\neq0 \]
则迭代法 \(x_{k+1}=\varphi(x_k)\) 是 p 阶收敛的
例题
1


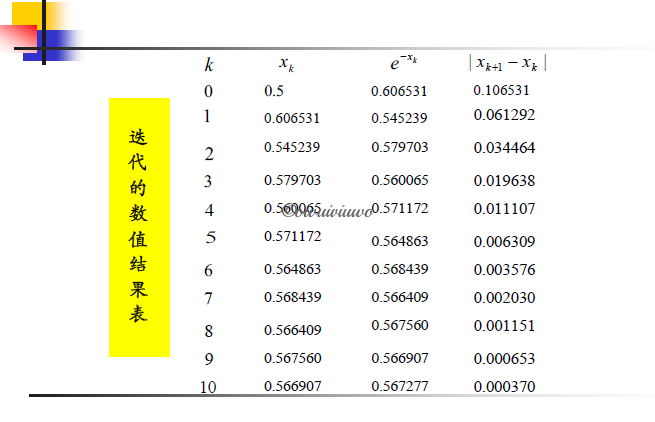
2

牛顿(Newton)法:

Newton 迭代法

Newton 迭代格式:设方程 \(f(x)=0\) 的根为 \(a\),且 \(f'(a)\neq0\),则迭代法
\[x_{k+1}=x_k-\frac{f(x_k)}{f'(x_k)}\;(k=0,1,2,\cdots) \]至少是平方收敛,并称该迭代格式为 Newton 迭代法。
类似的,可以使用导数的近似式 \(f'(x)\approx\frac{f(x_k)-f(x_{k-1})}{x_k-x_{k-1}}\) 替代 \(f'(x)\),可将其代入 Newton 迭代格式,得到割线法(弦截法)。
\[x_{k+1}=x_k-\frac{(x_k-x_{k-1})f(x_k)}{f(x_k)-f(x_{k-1})} \]割线法是超线性收敛的(\(p=\frac{1+\sqrt{5}}{2}\approx1.618\)),低于 Newton 法
此外,还有单步弦截法
\[x_{k+1}=x_k-\frac{(x_k-x_{0})f(x_k)}{f(x_k)-f(x_{0})} \]平行线法
\[x_{k+1}=x_k-\frac{f(x_k)}{f'(x_0)} \]例题
1






2
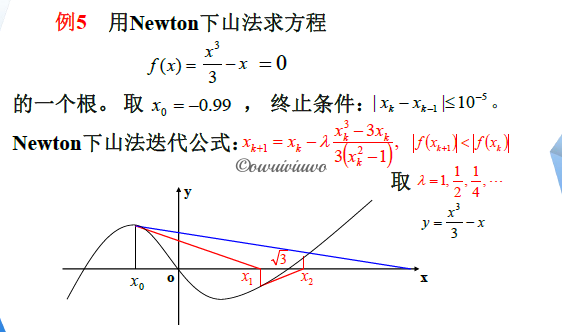

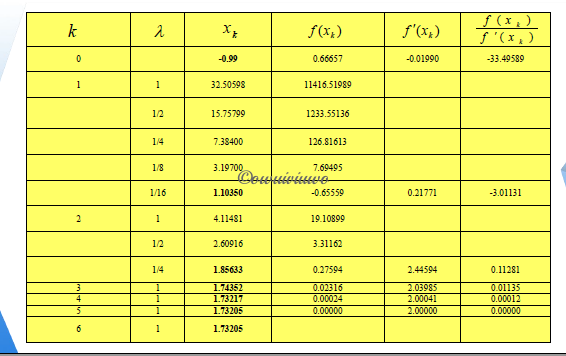

针对重根改进的 Newton 法:
设 \(a\) 是 \(f(x)=0\) 的 \(m\) 重根(满足 \(f(a)=f'(a)=f''(a)=\cdots=f^{(m-1)}(a)=0,\;f^{(m)}\neq0\) ),其中 \(m\geq2\) 是整数,则有 \(f(x)=(x-a)^mg(x)\),且 \(g(a)\neq0\)
此时,直接使用 Newton 法是线性收敛而不是平方收敛的
\[\varphi(x)=x-\frac{f(x)}{f'(x)}=x-\frac{(x-a)^mg(x)}{m(x-a)^{(m-1)}g(x)+(x-a)^mg'(x)} \\ \varphi'(x)=1-\frac{g(x)}{mg(x)+(x-a)g'(x)}-(x-a) [\frac{g(x)}{m\cdot g(x)+(x-a)g'(x)}]' \\ \varphi'(a)=1-\frac{g(a)}{m\cdot g(a)+0}-0=1-\frac{1}{m}\neq0 \]为了提高收敛的阶,可取 \(\varphi(x)=x-m\frac{f(x)}{f'(x)}\),从而 \(\varphi(a)=1-\frac{m}{m}=0\),则新迭代法至少是平方收敛的
例题

*多根区间上的逐次逼近法(应该不会考)
这里主要使用二分法





4.3 幂法
幂法(用于求绝对值最大的特征值)
幂法用于计算绝对值最大的特征值和对应的特征向量,对于单根和重根情形均有效。
概念:假定 n 阶方阵 A 具有 n 个线性无关的特征向量 \(x_1,x_2,\cdots,x_n\),且对应的特征值满足 \(|\lambda_1|>|\lambda_2|\geq\cdots\geq|\lambda_n|\),则对任一 n 维非零向量 \(v_0\) 经使用迭代过程
\[v_k=A^kv_0 \]计算可得
\[v_k=\alpha_1\lambda_1^kx_1,\quad \alpha_1\neq0,\quad \frac{v_k}{v_{k-1}}=\lambda_1 \]实际使用上,对幂法进行了改进,添加了规范化操作

算法过程
- 输入矩阵 \(A=(a_{ij})\),初始向量 \(v_0\),允许的误差 \(\epsilon\),最大迭代次数 \(N\)
- 置 \(k=1,\quad \mu=0\)
- 求 \(\max\{v_k\},\quad\max\{v_k\}\Rightarrow a\)
- 计算 \(u=v/a,\quad v=Au\),置 \(\max\{v_k\}=\lambda\)
- 若 \(|\lambda-\mu|<\epsilon\),输出 \(\lambda,u\),停机,否则跳转至 6
- 若 \(k<N\),置 \(k+1\Rightarrow k,\lambda\Rightarrow\mu\),转到 3,否则输出失败信息,停机
例题
利用幂法计算矩阵 A 的主(最大)特征值和相应的特征向量,其中 \(A=\begin{pmatrix}2&3&2\\10&3&4\\3&6&1\end{pmatrix}\),取 \(v_0=(0,0,1)^T\),迭代2次
解:
取 \(u_0=v_0=(0,0,1)^T\),则 \(u_1=Av_0=(2,4,1)^T\),且 \(\max\{u_1\}=-4\)
即 \(a=4\),于是 \(v_1=u_1/a=(0.5,1,0.25)^T\)
\(u_2=Av_1=(4.5,9,7.75)^T\) 且 \(\max\{u_2\}=9\)
即 \(a=9\),于是 \(v_2=u_2/a\approx(0.5,1,0.8611)\),可得 \(\lambda_1\approx9,x_1\approx(0.5,1.0,0.8611)^T\)
注:经过 8 次迭代可得 \(\lambda_1=11,x_1=(0.5,1.0,0.75)^T\)
反幂法
反幂法用于计算矩阵 A 按模最小的特征值及对应的特征向量

算法流程:
- 任取初始向量 \(v_0=u_0\neq0\)
- 计算 \(v_k=A^{-1}u_{k-1},\;(k=1,2,\cdots)\)
- \(\max\{v_k\}\Rightarrow m_k;\quad u_k=v_k/m_k\)
- 如果 \(k\) 从某时以后有 \(\frac{(v_k)_j}{(v_{k-1})_j}\approx c \;\;(常数)(j=1,2,\cdots,n)\),则取 \(\lambda_n\approx\frac{1}{c}\);而 \(u_k\) 就是与 \(\lambda_k\) 对应的特征向量
例题
1
用反幂法求矩阵 \(A=\begin{pmatrix}3&2\\4&5\end{pmatrix}\) 的按模最小的特征值和特征向量,精确至 6 位小数,迭代 1 次
解:
取 \(v_0=u_0=(1,1)^T\),由 \(v_1=A^{-1}u_0\),即 \(Av_1=u_0\)
得 \(v_1=(0.428571,-0.142857)^T\\m_1=\max\{v_1\}=0.428571\)
归一化得 \(u_1=(1.000000,-0.333333)^T\)
所以迭代 1 次得到的按模最小的特征值为 \(1/0.428571\),对应的特征向量为 \(u_1=(1.000000,-0.333333)^T\)
2
用反幂法求矩阵 \(A=\begin{pmatrix}3&2\\4&5\end{pmatrix}\) 的过程中,得到 \(u^{(8)}=\begin{pmatrix}1.000000\\-0.999999\end{pmatrix}\),则 A 的模最小的特征值的近似值为:
解:
由于 \(c=\max(u^{(8)}=1)\),则按模最小的特征值的近似值为 \(\lambda_1=\frac{1}{c}=1.000000\)
或者
依据特征值的概念与性质,可知有 \(Ax=\lambda x\),则
\[Au^{(8)}=\lambda_nu^{(8)}\approx \begin{pmatrix} 1\\-1 \end{pmatrix} \]则,可认为按模最小的特征值的近似值为 1。
4.4 共轭梯度法
共轭梯度法是以共轭方向作为搜索方向的一类算法,最初用于求解线性方程组,后来用于求解无约束最优化问题,是一种重要的数学优化方法。


*最速下降法(应该不会考)


共轭梯度法
下降方向 p 为上步下降方向与当前残量的线性组合,与 \(\beta\) 有关,步长为 \(\alpha\)
共轭梯度法最多迭代 n 步即可求得问题的精确解
算法的流程:
对于所给的初始向量 \(x_0\),\(r_0=p_0=b-Ax_0\)
\[\alpha_k=(r_k,r_k)/(Ap_k,p_k)\\ x_{k+1}=x_k+\alpha_kp_k\\ r_{k+1}=r_k-\alpha_kAp_k\\ \beta_k=(r_{k+1},r_{k+1})/(r_k,r_k)\\ p_{k+1}=r_{k+1}+\beta_kp_k\\ (k=0,1,2,\cdots) \]\((r_k,r_k)\) 表示内积运算。
例题

可见,迭代 2 步即可得到精确解