关于线段树的一点小笔记

关于线段树的一点小笔记

线段树：

1. 线段树是一棵天生支持单点修改、查询和区间查询的一棵完全二叉树，其单点修改、查询和区间修改的时间复杂度均为\(\Theta(\lg n)\)

2. 在区间修改时，如果我们暴力的修改并维护区间信息，那么时间复杂度将会退化为\(\Theta(n)\)，这显然不是我们想要的结果，但是，我们可以通过引用懒标记（lazytag）的思想来进行区间修改，具体的操作是这样的：

   1. 如果当前所在节点所表示的区间被目标区间所覆盖，则在当前节点上打上懒标记

   2. 如果当前所在节点所表示的区间没有被目标区间所覆盖，先下传懒标记，然后在递归到自区间进行修改

3. 通过懒标记的方式，我们可以将不支持区间修改的线段树改为为支持区间修改操作，这样的时间的复杂度也是\(\Theta(\lg n)\)，在所能接受的范围之内

4. 在维护区间或在处理多个懒标记的过程中，我们应当正确处理区间之间和懒标记之间的关系，例如P1471 方差这道题，如果先处理区间和，在处理区间平方和的话，就会导致区间平方和的错误，再比如P7453 大魔法师这一道题，如果针对\(a,b,c\)的懒标记没有正确的处理，就会导致时间复杂度退化为\(O(n)\)的问题

5. 线段树并不是万能的，当需要维护的信息满足以下几个条件时，我们才可以使用线段树：

   1. 所维护的信息本身可以快速的合并

   2. 为了达成条件，需要维护一些其它的信息

6. 并不是所有的线段树都支持区间修改，只有当懒标记的信息可以合并时，区间修改才有意义

7. 平衡树已经死了：当平衡树所涉及 的操作没有区间翻转时，我们就可以使用线段树来代替平衡树维护，例如大名鼎鼎的平衡树模板题P3369【模板】普通平衡树，就完全可以用线段树来进行操作，既简单，又方便。

线段树的衍生数据结构：

一、树状数组：

1. 树状数组 \(\subset\) 线段树：

   1. 树状数组可以看做是没有右儿子的线段树，如下图所示（图中蓝色虚线代表不存在的节点）：

   

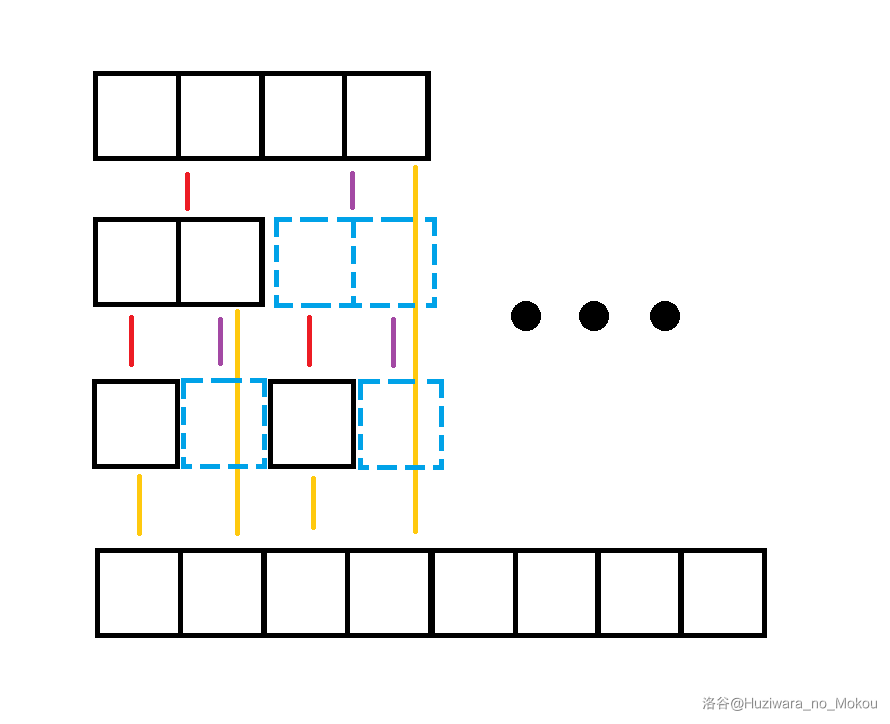
   2. 树状数组天生支持单点修改和单点查询

   3. 在源数据可以差分的情况下，树状数组也支持区间修改和区间查询

二、二进制字典树（目前还不会）：

一些线段树的骚操作和一些奇怪的线段树：

一、动态开点：

1. 在平常建立线段树的时候，我们经常把节点\(p\)的左右儿子标号为\(p*2\)和\(p*2+1\)，但是在最坏情况下这样建树就需要至少\(4n\)的节点才能保证访问时数组不越界（当然，用指针的同学除外），于是这时候，我们就需要一个骚操作来节省空间，这个骚操作也就是动态开点，他可以使得线段树的最坏空间复杂度为\(O(2n+1)\)

2. 动态开点的核心思想是：当你需要一个叶子节点时，若该叶子节点不存在，则把它和它的所在区间全部建立出来

3. 动态开点模板板子：

struct SegmentTree{
    int data;//指需要维护的数据，并没有具体的含义
    int lc,rc;
};
SegmentTree seg[MAX_SIZE];
int tot=0;//已添加的节点个数
int build(){//建立一个新的节点
    ++tot;
    seg[tot].lc = seg[tot].rc = seg[tot].data = 0;
    return tot;
}
void insert(int p,int l,int r,int val,int data){//插入一个节点
    //p:表示当前所在节点下标
    //l:表示当前节点所表示区间的左端点
    //r:表示当期节点所表示区间的右端点
    //val:表示目标位置
    //data:表示目标位置要填的数据
    if(l==r){
        seg[p].data = data;
        return ;
    }
    int mid = (l+r)>>1;
    if(val<=mid){
        if(!seg[p].lc)
            seg[p].lc = build();
        insert(seg[p].lc,l,mid,val);
    }
    else{
        if(!seg[p].rc)
            seg[p].rc = build();
        insert(seg[p].rc,mid+1,r,val);
    }
    pushup(p);
}

二、势能线段树：

1. 在线段树的性质中，我们讲到了使用线段树的两个限制条件，然而在某些操作下，我们可以通过线段树对序列进行维护，这些操作通常有一个隐含的“上界”，就相当于有一个“势能”，当操作达到或者超过了这个上线，也就是它的势能小于等于0时，相应的操作就会退化失效，从而可以用线段树维护，我们也把这样的线段树叫做“势能线段树”

2. 在势能线段树中，我们要考虑以下几个要点：

   1. 现在的势能是多少

   2. 势能为零时如何操作

   3. 如果还有区间势能不为零，则暴力递归修改下去

3. 时间复杂度均摊下来通常为\(\Theta(\lg n)\)

三、值域线段树：

1. 是平衡树的主要竞争对手之一，其主要思想为，把每一个节点看做一个桶，这样的话区间\([l,r]\)就表示在区间内部的数值，然后节点总维护的是这个桶中