标签：03 函数 min 灰度变换 模糊 mu 图像处理 集合 隶属

混合空间增强法

将多种图像增强方法结合起来，完成困难的图像增强任务

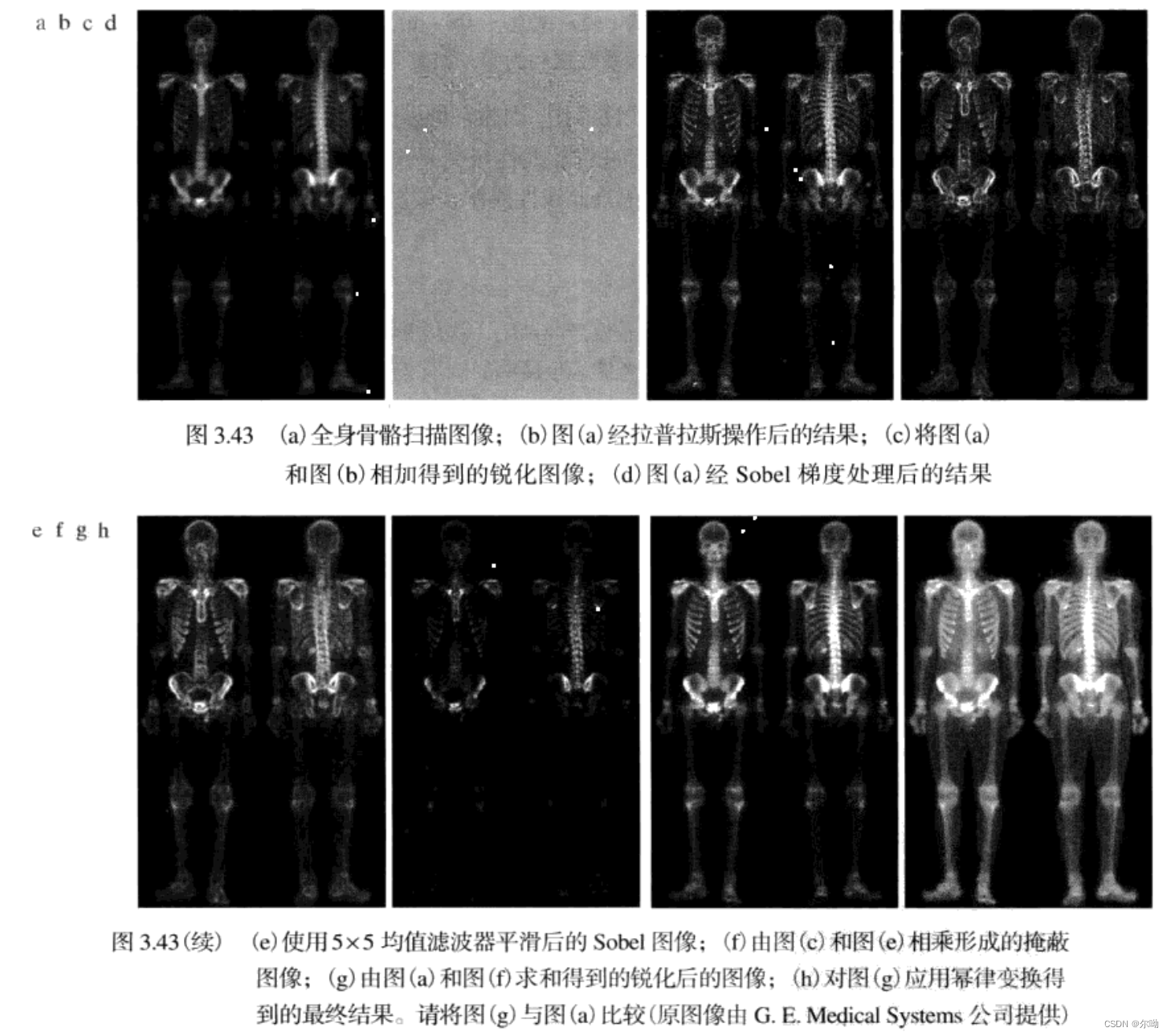
使用模糊技术进行灰度变换和空间滤波

目的：例如将人分为年轻人和非年轻人，使用一个确定的阈值例如20岁，那么20岁过1秒的人也属于非年轻人，我们需要更加弹性的在年轻和非年轻之间过渡

模糊集合论原理

\(Z\)是一个元素集，\(z\)表示\(Z\)的一类元素，即\(Z = \{z\}\)，该集合称为论域，模糊集合\(A\)由隶属度函数\(\mu_A(z)\)来表征：

\[A = \{z,\mu_A(z)|z \in Z\} \]

当隶属度函数值为1表示该元素是集合的完全成员，隶属度函数值位于0和1之间表示在集合中的隶属度等级为隶属度函数值，隶属度函数值为0表示该元素不属于该集合

• 空集：\(Z\)中的隶属度函数值为0，模糊集合为空集；
• 相等：当且仅当对于所有的\(z \in Z,\mu_A(z) = \mu_B(z)\)，则称两个模糊集合\(A\)和\(B\)相等；
• 补集：由\(\overline{A}\)或\(NOT(A)\)表示模糊集合\(A\)的补集，定义其隶属度函数为：

\[\mu_{\overline{A}}(z) = 1 - \mu_A(z) \]

• 子集：当且仅当对于所有的\(z \in Z\)有：

\[\mu_A(z) \leq \mu_B(z) \]

此时，模糊集合\(A\)是模糊集合\(B\)的子集；

• 并集：
• 对于所有的\(z \in Z\)，具有隶属度函数：

\[\mu_U(z) = max[\mu_A(z),\mu_B(z)] \]

的并集\(U\)表示为\(A \bigcup B\)或\(A\ OR\ B\)

• 对于所有的\(z \in Z\)，具有隶属度函数：

\[\mu_I(z) = min[\mu_A(z),\mu_B(z)] \]

的交集\(I\)表示为\(A \bigcap B\)或\(A\ AND\ B\)

模糊集合应用

假设生的水果是绿色的，半熟的水果是黄色的，成熟的水果是红色的，对应规则集：

• \(R_1\)：IF颜色是绿色，THEN水果是生的
• \(R_2\)：IF颜色是黄色，THEN水果是半熟的
• \(R_3\)：IF颜色是红色，THEN水果是熟的

颜色采用波长这一值来表示，下图表示不同的波长对应不同颜色的隶属度，也就是输入的隶属度函数：

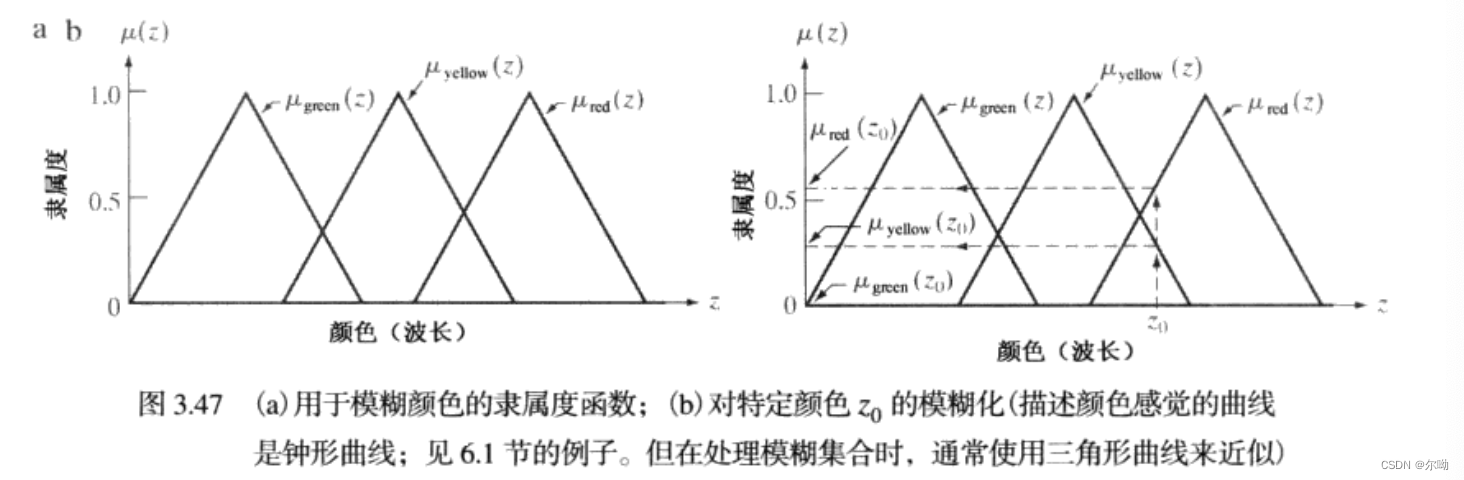
输出本身也是模糊的：

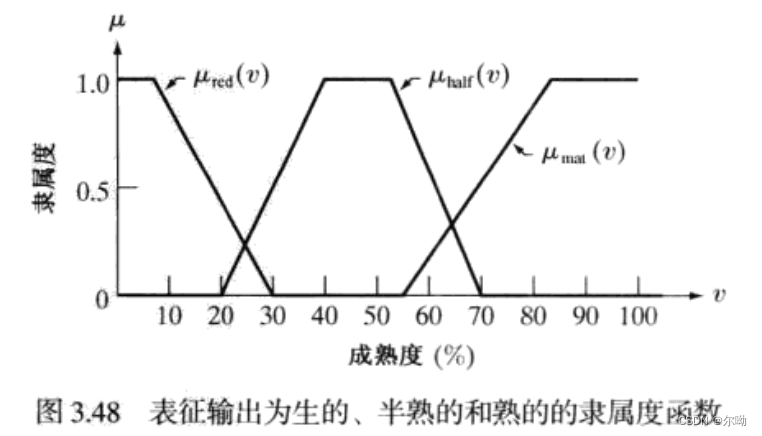
以红色\(AND\)成熟规则\(R_3\)为例，这是一个二维的隶属度函数，表示为一个笛卡尔积\((z,v)\)到\([0,1]\)的映射：

\[\mu_3(z,v) = min\{\mu_{red}(z),\mu_{mat}(v)\} \]

上式是一个通用解，此时一个特定的输入\(z_0\)，此时用\(Q_3(v)\)表示，\(c = \mu_{red}(z_0)\)，唯一的变量为\(v\)：

\[Q_3(v) = min\{\mu_{red}(z_0),\mu_{mat}(z_0,v)\} \]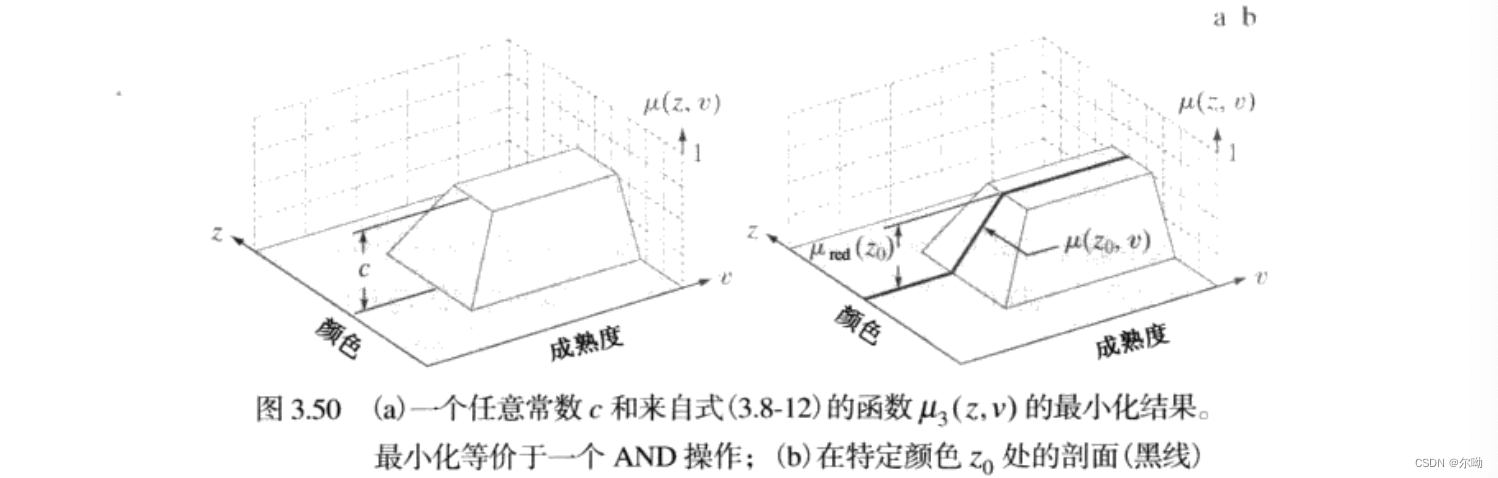

同理，我们可以得到另外两个规则和输入\(z_0\)导致的模糊响应：

\[Q_1(v) = min\{\mu_{green}(z_0),\mu_{1}(z_0,v)\} \\ Q_2(v) = min\{\mu_{yellow}(z_0),\mu_{2}(z_0,v)\} \]

由于三个规则之间是通过\(OR\)操作连接起来的：

\[Q = Q_1 \ OR \ Q_2 \ OR \ Q_3 \]

所以我们可以得到结果如下：\(r = \{1,2,3\},s = \{绿色,黄色,红色\}\)，见下图

\[Q(v) = \mathop{max}\limits_{r} \left\{ \mathop{min}\limits_{s} \left\{ \mu_s(z_0),\mu_r(z_0,v)\right\}\right\} \]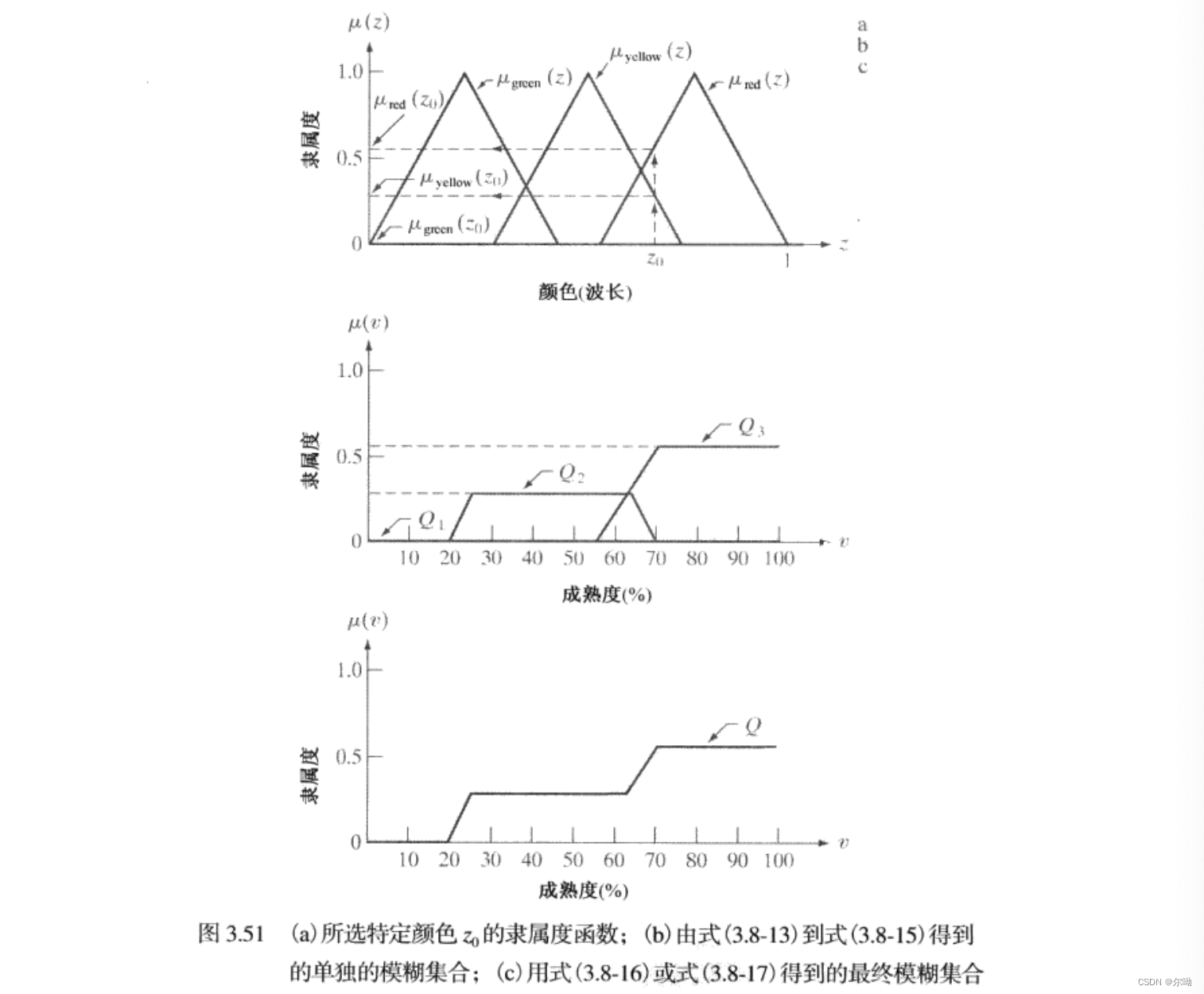

之后进行去模糊操作求出一个干脆的输出\(v_0\)，计算集合的重心，假设\(Q(v)\)有\(K\)种取值：

\[v_0 = \frac{\sum_{v = 1}^KvQ(v)}{\sum_{v = 1}^KQ(v)} \]

得到\(v_0 = 72.3\)，指出给定的颜色\(z_0\)成熟度约为\(72\%\)

总结：

• 模糊输入：对于每个标量输入，例如颜色，使用隶属度函数找到相应的模糊值；
• 合并各个部分的输出，利用模糊集合操作交和并，例如前提为绿色或坚硬，合并时用\(OR\)；
• 每一个规则，例如红色\(AND\)成熟，前提和输出之间使用\(AND\)连接；
• 将不同的规则聚合起来，使用\(OR\)操作；
• 将最后输出的模糊集合去模糊操作，得到一个干脆的标量输出，例如计算重心；

使用模糊集合进行灰度变换

考虑如下的一个例子：

• IF一个像素是暗的，THEN使它较暗；
• IF一个像素是灰的，THEN使它仍是灰的；
• IF一个像素是亮的，THEN使它较亮；
  最终得到的\(Q\)如下右图所示：
  
  对于任何输入\(z_0\)，输出\(v_0\)由下式给出：

\[v_0 = \frac{\mu_{dark}(z_0) \times v_d + \mu_{gray}(z_0) \times v_g + \mu_{bright}(z_0) \times v_b}{\mu_{dark}(z_0) + \mu_{gray}(z_0) + \mu_{bright}(z_0)} \]

使用模糊集合进行空间滤波

例如一个模糊集合概念的边缘提取算法：如果一个像素属于平滑区，则令其为白色，否则令其为黑色；这个概念可以翻译为如下的规则集：

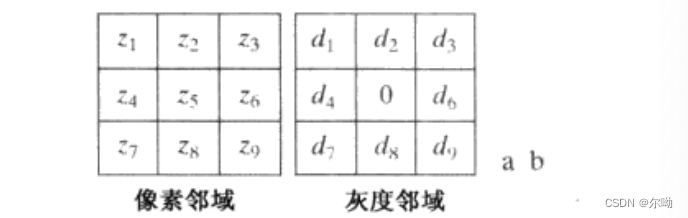
如图为邻域，假设像素标为\(z_i,i = 1,2,\cdots,9\)，\(d_i\)表示第\(i\)个邻点和中心点的灰度差\(d_i = z_i - z_5\)

• \(IF\ d_2 = 0 \ AND \ d_6 = 0\ THEN\ z_5 = 白色\)
• \(IF\ d_6 = 0 \ AND \ d_8 = 0\ THEN\ z_5 = 白色\)
• \(IF\ d_8 = 0 \ AND \ d_4 = 0\ THEN\ z_5 = 白色\)
• \(IF\ d_4 = 0 \ AND \ d_2 = 0\ THEN\ z_5 = 白色\)
• \(ELSE\ z_5 = 黑色\)

标签：03,函数,min,灰度变换,模糊,mu,图像处理,集合,隶属
From： https://www.cnblogs.com/eryoyo/p/16724765.html