模块导图

知识剖析
随机事件与概率
① 有限样本空间与随机事件
(1) 我们把对随机现象的实现和对它的观察称为随机试验,简称试验,常用字母\(E\)表示,
我们把随机试验\(E\)的每个可能的基本结果称为样本点,全体样本点的集合称为\(E\)试验的样本空间.用\(Ω\)表示样本空间,用\(ω\)表示样本点.如果一个随机试验有\(n\)个可能结果结果\(ω_1\),\(ω_2\) ,… ,\(ω_n\),则称样本空间\(Ω=\{ω_1 ,ω_2 ,… ,ω_n\}\)为有限样本空间.
(2) 事件
样本空间\(Ω\)的子集称为随机事件,简称事件,并把只包含一个样本点的事件成为基本事件.随机事件一般用大写字母\(A\) ,\(B\) ,\(C\) ,…表示.
各种事件
必然事件,不可能事件,随机事件.
在\(12\)件瓷器中,有\(10\)件一级品,\(2\)件二级品,从中任取\(3\)件.
(1) “\(3\)件都是二级品”是什么事件?
(2) “\(3\)件都是一级品”是什么事件?
(3)“至少有一件是一级品”是什么事件?
解 (1)因为\(12\)件瓷器中,只有\(2\)件二级品,取出\(3\)件都是二级品是不可能发生的,故是不可能事件.
(2)“\(3\)件都是一级品”在题设条件下是可能发生也可能不发生的,故是随机事件.
(3)“至少有一件是一级品”是必然事件,因为\(12\)件瓷器中只有\(2\)件二级品,取三件必有一级品.
事件的关系和运算
1 包含
一般地,若事件\(A\)发生,则事件\(B\)一定发生,我们就称事件\(A\)包含于事件\(B\),记作\(A\subseteq B\);
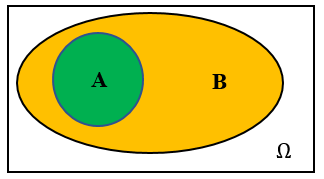
2 并事件(或和事件)
一般地,事件\(A\)与事件\(B\)至少有一个发生,我们称这个事件为事件\(A\)与事件\(B\)的并事件(或和事件),记作\(A\cup B\)(或\(A+B\)).
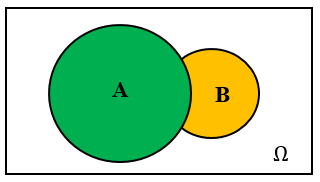
3 交事件(或积事件)
一般地,事件\(A\)与事件\(B\)同时发生,我们称这样一个事件为事件\(A\)与事件\(B\)的交事件(或积事件),记作\(A\cap B\)(或\(AB\)).
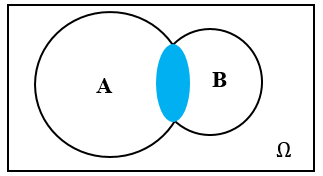
4 互斥
一般地,如果事件\(A\)与事件\(B\)不能同时发生,也就是\(A\cap B\)是一个不可能事件,即\(A\cap B=\varnothing\),则称事件\(A\)与事件\(B\)互斥(或互不相容).
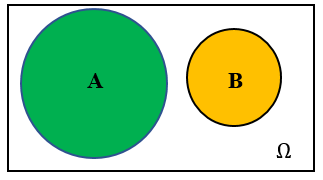
5 对立
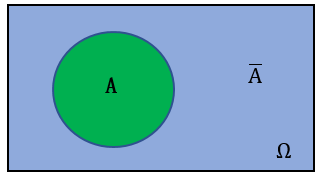
一般地,如果事件\(A\)与事件\(B\)在任何一次试验中有且仅有一个发生,即\(A\cup B=Ω\)且\(A\cap B=\varnothing\),则称事件\(A\)与事件\(B\)互为对立,事件\(A\)的对立事件记为\(\overline{A}\).
综上所述,事件的关系或运算的含义,以及相应的符号表示如下
| 事件的关系或运算 | 含义 | 符号表示 |
|---|---|---|
| 包含 | \(A\)发生导致\(B\)发生 | \(A\subseteq B\) |
| 并事件(和事件) | \(A\)与\(B\)至少一个发生 | \(A\cup B\)或 \(A+B\) |
| 交事件(积事件) | \(A\)与\(B\)同时发生 | \(A\cap B\)或\(AB\) |
| 互斥 | \(A\)与\(B\)不能同时发生 | \(A\cap B=\varnothing\) |
| 对立 | \(A\)与\(B\)有且仅有一个发生 | \(A\cup B=Ω\)且\(A\cap B=\varnothing\) |
类似地,我们可以定义多个事件的和事件及其积事件.例如,对于三个事件\(A\),\(B\),\(C\),\(A\cup B\cup C\)(或\(A+B+C\))发生当且仅当\(A\),\(B\),\(C\)中至少一个发生,\(A\cap B\cap C\)(或\(ABC\))发生当且仅当\(A\),\(B\),\(C\)同时发生,等等.
古典概型
(1) 古典概型的特点
有限性:样本空间的样本点只有有限个;
等可能性:每个样本点发生的可能性相等.
(2) 古典概型事件\(A\)的概率
\[P(A)=\dfrac{\text { 事件 } A \text { 的样本点个数 }}{\text { 样本空间 } \Omega \text { 的样本点个数 }} \]
概率的基本性质
性质1 对任意事件\(A\),都有\(P(A)≥0\);
性质2 必然事件的概率为1,不可能事件的概率为\(0\);
性质3 若事件\(A\)与事件\(B\)互斥时,则\(P(A\cup B)=P(A)+P(B)\);
性质4 若事件\(A\)与事件\(B\)对立事件,则\(P(B)=1-P(A)\) ,\(P(A)=1-P(B)\);
性质5 如果\(A\subseteq B\),那么\(P(A)≤P(B)\);
性质6 设\(A\) ,\(B\)是一个随机试验中的两个事件,有\(P(A\cup B)=P(A)+P(B)-P(A\cap B)\).
经典例题
【题型一】对各种事件、事件的关系和运算的理解
【典题1】 从\(5\)位男生和\(2\)位女生共\(7\)位同学中任意选派\(3\)人,属必然事件的是( )
A.\(3\)位都是女生 \(\qquad \qquad \qquad \qquad\) B.至少有\(1\)位是女生
C.\(3\)位都不是女生 \(\qquad \qquad \qquad \qquad\) D.至少有\(1\)位是男生
【解析】由于从\(5\)位男生和\(2\)位女生共7位同学中任意选派\(3\)人,
有\(3\)位男生,\(2\)位男生\(1\)位女生,\(1\)位男生\(2\)位女生,共三种情况
故\(A\)为不可能事件,\(B\),\(C\)为随机事件,\(D\)为必然事件.
故答案为 \(D\).
【典题2】 从装有十个红球和十个白球的罐子里任取\(2\)球,下列情况中是互斥而不对立的两个事件是( )
A.至少有一个红球;至少有一个白球
B.恰有一个红球;都是白球
C.至少有一个红球;都是白球
D.至多有一个红球;都是红球
【解析】对于\(A\),“至少有一个红球”可能为一个红球、一个白球,“至少有一个白球”可能为一个白球、一个红球,故两事件可能同时发生,所以不是互斥事件;
对于\(B\),“恰有一个红球”,则另一个必是白球,与“都是白球”是互斥事件,而任取\(2\)个球还有都是红球的情形,故两事件不是对立事件;
对于\(C\),“至少有一个红球”为都是红球或一红一白,与“都是白球”显然是对立事件;
对于\(D\),“至多有一个红球”为都是白球或一红一白,与“都是红球”是对立事件.
【点拨】对立事件是互斥事件,互斥事件不一定是对立事件.
【典题3】 如果事件\(A\) ,\(B\)互斥,记\(\bar{A}\),\(\bar{B}\)分别为事件\(A\) ,\(B\)的对立事件,那么( )
A.\(A\cup B\)是必然事件 \(\qquad \qquad \qquad \qquad\) B. \(\bar{A}\cup\bar{B}\)是必然事件
C. \(\bar{A}\)与\(\bar{B}\)一定互斥 \(\qquad \qquad \qquad \qquad\) D.\(\bar{A}\)与\(\bar{B}\)一定不互斥
【解析】 用\(Venn\)图解决此类问题较为直观.如右图所示,\(\bar{A}\cup \bar{B}\)是必然事件,故选\(B\).

【点拨】利用集合的关系看事件之间的关系会更直观.
【题型二】求古典概型
【典题1】 先后投掷两枚骰子,出现的点数记作\((m ,n)\),设\(X=m+n\).
(1)求\(m=n\)的概率;
(2)试列举出\(X≤6\)的所有可能的结果;
(3)求\(X≤3\)或\(X>6\)的概率.
【解析】(Ⅰ)先后投掷两枚骰子,出现的点数情况有:
\((1,1),(1,2),(1,3),(1,4),(1,5),(1,6)\),
\((2,1),(2,2),(2,3),(2,4),(2,5),(2,6)\),
\((3,1),(3,2),(3,3),(3,4),(3,5),(3,6)\),
\((4,1),(4,2),(4,3),(4,4),(4,5),(4,6)\),
\((5,1),(5,2),(5,3),(5,4),(5,5),(5,6)\),
\((6,1),(6,2),(6,3),(6,4),(6,5),(6,6)\),
共有\(36\)种可能结果,
而\(m=n\)有\(6\)结果,为\((1 ,1) ,(2 ,2) ,(3 ,3) ,(4 ,4) ,(5 ,5) ,(6 ,6)\),
(也可以使用树状图
 )
)
所以 \(P(m=n)=\dfrac{6}{36}=\dfrac{1}{6}\),
(Ⅱ)\(X≤6\)的所有可能的结果有\((1 ,1) ,(1 ,2) ,(1 ,3) ,(1 ,4) ,(1 ,5)\),
\((2 ,1) ,(2 ,2) ,(2 ,3) ,(2 ,4) ,(3 ,1)\),
\((3 ,2) ,(3 ,3) ,(4 ,1) ,(4 ,2) ,(5 ,1)\) ,
共有\(15\)种情况,
(Ⅲ)由(Ⅰ)(Ⅱ)可知,\(X≤3\)的所有可能的结果有\(3\)种,为\((1 ,1)、(1 ,2)、(2 ,1)\),
\(X>6\)的所有可能的结果有\(36-21=15\),
\(p(X \leq 3 \text { 或 } X>6)=\dfrac{3}{36}+\dfrac{21}{36}=\dfrac{2}{3}\).
【点拨】根据古典概型事件\(A\)的概率 \(P(A)=\dfrac{\text { 事件 } A \text { 的样本点个数 }}{\text { 样本空间 } \Omega \text { 的样本点个数 }}\),一般都用穷举法,比如列树状图或者把每个样本点一一列举,关键就要做到不重不漏,在一一列举的时候最好能够按照一定的规律进行.
【典题2】 任取三个整数,至少有一个数为偶数的概率为 \(\underline{\quad \quad}\).
【解析】方法一 任取三个整数,共有八种情况:

其中至少有一个数为偶数的情况有\(7\)种,所以所求概率为\(\dfrac{7}{8}=0.875\),
方法二 任取三个整数,共有八种情况,设“都是奇数”为事件\(A\),“至少有一个数为偶数”事件\(B\),而事件\(A\) ,\(B\)是对立事件, \(P(A)=\dfrac{1}{8}\),故 \(P(B)=1-P(A)=\dfrac{7}{8}=0.875\).
【点拨】
① 因为是取三个整数,列树状图时有\(3\)列.
② 方法一从正面入手,方法二从反面切入,往后题目中出现“至少”,“至多”等字眼,都可以从反面进行思考。
【典题3】 一个正方体,它的表面涂满了红色.在它的每个面上切两刀可得\(27\)个小立方块,从中任取两个,其中恰有\(1\)个一面涂有红色,\(1\)个两面涂有红色的概率为\(\underline{\quad \quad}\) .
【解析】根据题意,分析可得:
在分割下来的\(27\)个完全相等的小正方体中,有\(6\)个只有一面有红色,有\(12\)个两面有红色,8块有\(3\)面红色,而还有一个没有红色;
则从中任取\(2\)个,其中\(1\)个恰有一面涂有红色,另\(1\)个恰有两面涂有红色的情况有\(12×6\)种;
而从\(27\)块中任取两块,有\(27×26\)种情况;
则从中任取\(2\)个,其中\(1\)个恰有一面涂有红色,另\(1\)个恰有两面涂有红色的概率为\(\dfrac{12 \times 6}{27 \times 26}=\dfrac{8}{39}\).
【典题4】 数学与文学有许多奇妙的联系,如诗中有回文诗:“儿忆父兮妻忆夫”,既可以顺读也可以逆读,数学中有回文数,如\(343\)、\(12521\)等,两位数的回文数有\(11、22、33、…、99\)共\(9\)个,则三位数的回文数中为偶数的概率是 \(\underline{\quad \quad}\) .
【解析】三位数的回文数为\(ABA\),
\(A\)有\(1\)到\(9\)共\(9\)种可能,即\(1B1\)、\(2B2\)、\(3B3\)…
\(B\)共有\(0\)到\(9\)共\(10\)种可能,即\(A0A\)、\(A1A\)、\(A2A\)、\(A3A\)、…
共有\(9×10=90\)个,
其中偶数为\(A\)是偶数,共\(4\)种可能,即\(2B2\),\(4B4\),\(6B6\),\(8B8\),
\(B\)共有\(0\)到\(9\)共\(10\)种可能,即\(A0A\)、\(A1A\)、\(A2A\)、\(A3A\)、…
其有\(4×10=40\)个,
\(\therefore\)三位数的回文数中,偶数的概率\(P=\dfrac{40}{90}=\dfrac{4}{9}\).
【题型三】概率的基本性质
【典题1】 有一个公用电话亭,里面有一部电话,在观察使用这部电话的人的流量时,设在某一时刻,有\(n\)个人正在使用电话或等待使用的概率为\(P(n)\),且\(P(n)\)与时刻t无关,统计得到 \(P(n)=\left\{\begin{array}{l}
\left(\dfrac{1}{2}\right)^n \cdot P(0), 1 \leq n \leq 6 \\
0, n \geq 7
\end{array}\right.\),那么在某一时刻,这个公用电话亭里一个人也没有的概率\(P(0)\)的值是\(\underline{\quad \quad}\).
【解析】由题意知:本公用电话亭每次不超过\(7\)人正在使用电话或等待使用,
\(\therefore\)“有\(0、1、2、3、4、5、6\)个人正在使用电话或等待使用”是必然事件,
\(\therefore\)随机变量\(n\)的值可取\(0,1,2,3,4,5,6\),
即\(p(0)+p(1)+p(2)+p(3)+p(4)+p(5)+p(6)=1\)
\(\therefore p(0)+\dfrac{1}{2} p(0)+\dfrac{1}{4} p(0)+\dfrac{1}{8} p(0)+\dfrac{1}{16} p(0)+\dfrac{1}{32} p(0)+\dfrac{1}{64} p(0)=1\),
\(\therefore p(0)=\dfrac{64}{127}\).
故答案为: \(\dfrac{64}{127}\).
【典题2】 袋中有\(12\)个小球,分别为红球、黑球、黄球、绿球,从中任取一球,得到红球的概率是\(\dfrac{1}{3}\),得到黑球或黄球的概率是\(\dfrac{5}{12}\),得到黄球或绿球的概率也是\(\dfrac{5}{12}\),试求得到黑球、得到黄球、得到绿球的概率各是多少?
【解析】从袋中任取一球,记事件“得到红球”“得到黑球”“得到黄球”“得到绿球”分别为\(A\) ,\(B\) ,\(C\) ,\(D\),
则\(P(A)=\dfrac{1}{3}\)\(,P(B\cup C)=P(B)+P(C)=\dfrac{5}{12}\),
\(P(C\cup D)=P(C)+P(D)=\dfrac{5}{12}\),
\(P(B \cup C \cup D)=P(B)+P(C)+P(D)=1-P(A)=1-\dfrac{1}{3}=\dfrac{2}{3}\),
解 \(\left\{\begin{array}{c}
P(B)+P(C)=\dfrac{5}{12} \\
P(C)+P(D)=\dfrac{5}{12} \\
P(B)+P(C)+P(D)=\dfrac{2}{3}
\end{array}\right.\), 得\(P(B)=\dfrac{1}{4}\),\(P(C)=\dfrac{1}{6}\), \(P(D)=\dfrac{1}{4}\),
即得到黑球,得到黄球,得到绿球的概率分别为\(\dfrac{1}{4}\),\(\dfrac{1}{6}\),\(\dfrac{1}{4}\).
巩固练习
1(★) 将一根长为\(a\)的铁丝随意截成三段,构成一个三角形,此事件是( )
A.必然事件 \(\qquad \qquad \qquad\) B.不可能事件 \(\qquad \qquad \qquad\) C.随机事件 \(\qquad \qquad \qquad\) D.不能判定
2(★) 在\(1,2,3,…,10\)这\(10\)个数字中,任取\(3\)个数字,那么“这三个数字的和大于\(6\)”这一事件是( )
A.必然事件 \(\qquad \qquad\) B.不可能事件 \(\qquad \qquad\) C.随机事件 \(\qquad \qquad\) D.以上选项均不正确
3(★) 下列每对事件是互斥事件的个数是( )
(1)将一枚均匀的硬币抛\(2\)次,记事件\(A\):两次出现正面;事件\(B\):只有一次出现正面
(2)某人射击一次,记事件\(A\):中靶,事件\(B\):射中\(9\)环
(3)某人射击一次,记事件\(A\):射中环数大于\(5\);事件\(B\):射中环数小于\(5\).
A.\(0\)个 \(\qquad \qquad \qquad \qquad\) B.\(1\)个 \(\qquad \qquad \qquad \qquad\) C.\(2\)个 \(\qquad \qquad \qquad \qquad\) D.\(3\)个
4(★) 袋中有白球\(2\)个,红球\(3\)个,从中任取两个,则互斥且不对立的两个事件是( )
A.至少有一个白球;都是白球
B.两个白球;至少有一个红球
C.红球、白球各一个;都是白球
D.红球、白球各一个;至少有一个白球
5(★) 设\(M\)、\(N\)为两个随机事件,如果\(M\)、\(N\)为互斥事件,那么( )
A. \(\bar{M} \cup \bar{N}\)是必然事件 \(\qquad \qquad \qquad \qquad\) B.\(M\cup N\)是必然事件
C.\(\bar{M}\)与\(\bar{N}\)一定为互斥事件 \(\qquad \qquad \qquad \qquad\) D.\(\bar{M}\)与\(\bar{N}\)一定不为互斥事件
6(★) 已知一次试验,事件\(A\)与事件\(B\)不能同时发生且 \(A\),\(B\) 至少有一个发生,又事件\(A\)与事件\(C\)不能同时发生.若 \(P(B)=0.6\), \(P(C)=0.2\),则 \(P(A \cup C)=\) ( )
A.\(0.6\) \(\qquad \qquad \qquad \qquad\) B.\(0.5\) \(\qquad \qquad \qquad \qquad\) C.\(0.4\) \(\qquad \qquad \qquad \qquad\)D.\(0.3\)
7(★) 先后抛掷两枚骰子,设出现的点数之和是\(8\),\(7\),\(6\)的概率依次为\(P_1\),\(P_2\),\(P_3\),则( )
A.\(P_1=P_2<P_3\) \(\qquad \qquad\) B.\(P_3<P_2<P_1\) \(\qquad \qquad\) C.\(P_3=P_1<P_2\) \(\qquad \qquad\)D.\(P_3=P_1>P_2\)
8(★★) 从集合\(A=\{-1,\dfrac{1}{2},2\}\)中随机选取一个数记为\(k\),从集合\(B=\{\dfrac{1}{2},\dfrac{3}{2},2\}\)中随机选取一个数记为\(a\),则\(a^k>1\)的概率为( )
A.\(\dfrac{1}{3}\) \(\qquad \qquad \qquad \qquad\) B.\(\dfrac{2}{3}\) \(\qquad \qquad \qquad \qquad\) C.\(\dfrac{7}{9}\) \(\qquad \qquad \qquad \qquad\) D.\(\dfrac{5}{9}\)
9(★) [多选题]抛掷两枚质地均匀的骰子,有如下随机事件:\(A=\) “至少一枚点数为\(1\)”,\(B=\)“两枚骰子点数一奇一偶”,\(C=\)“两枚骰子点数之和为\(8\)”,\(D=\)“两枚骰子点数之和为偶数”.判断下列结论,正确的有 ( )
A.\(A \subseteq B\) \(\qquad \qquad \qquad \qquad\qquad \qquad\) B.\(B\) ,\(D\) 为对立事件
C. \(A\),\(C\) 为互斥事件 \(\qquad \qquad \qquad\qquad \qquad\) D.\(A\) ,\(D\) 相互独立
10(★) 掷一枚质地均匀的骰子,观察出现的点数,设“出现\(3\)点”、“出现\(6\)点”分别为事件\(A\)、\(B\),已知\(P(A)=P(B)=\dfrac{1}{6}\),则出现点数为\(3\)的倍数的概率为\(\underline{\quad \quad}\).
11(★) 如图所示,靶子由一个中心圆面Ⅰ和两个同心圆环Ⅱ、Ⅲ 构成,射手命中Ⅰ、Ⅱ、Ⅲ的概率分别为\(0.25\)、\(0.20\)、\(0.35\),则不命中靶的概率是\(\underline{\quad \quad}\).

12(★) 事件\(A\),\(B\)互斥,它们都不发生的概率为\(\dfrac{2}{5}\),且\(P(A)=2P(B)\),则\(P(\bar{A})=\)\(\underline{\quad \quad}\).
13(★) 经过某十字路口的汽车,它可能继续直行,也可能向左转或向右转,如果这三种可能性大小相同,那么三辆汽车经过这个十字路口,至少有两辆车向左转的概率为\(\underline{\quad \quad}\).
14(★★) 若连掷两次骰子,分别得到的点数是\(m\)、\(n\),将\(m\)、\(n\)作为点\(P\)的坐标,则点\(P\)落在区域\(|x-2|+|y-2| \leqslant 2\)内的概率是\(\underline{\quad \quad}\).
15(★★) 如图所示,\(A\)、\(B\)是边长为\(1\)的小正方形组成的网格的两个顶点,在格点中任意放置点\(C\),恰好能使其构成\(△ABC\)且面积为\(1\)的概率是\(\underline{\quad \quad}\).

16(★) 抛掷一枚均匀的骰子,事件\(A\)表示“朝上一面的点数是偶数”,事件\(B\)表示“朝上一面的点数不超过\(4\)”,求\(P(A\cup B)\).
17(★★) 某城市为鼓励人们绿色出行,乘坐地铁,地铁公司决定按照乘客经过地铁站的数量实施分段优惠政策,不超过\(9\)站的地铁票价如表:
| 乘坐站数\(x\) | \(0<x≤3\) | \(3<x≤6\) | \(6<x≤9\) |
|---|---|---|---|
| 票价(元) | \(1\) | \(2\) | \(3\) |
现有甲、乙两位乘客同时从起点乘坐同一辆地铁,已知他们乘坐地铁都不超过\(9\)站,且他们各自在每个站下车的可能性是相同的.
(1)若甲、乙两人共付费\(2\)元,则甲、乙下车方案共有多少种?
(2)若甲、乙两人共付费\(4\)元,求甲比乙先到达目的地的概率.
参考答案
-
【答案】\(C\)
【解析】将一根长为a的铁丝随意截成三段,构成一个三角形,这个事件是可能发生的事件,但不是必然事件.所以事件是随机事件.
故答案选择\(C\). -
【答案】\(C\)
【解析】 从\(10\)个数字中取\(3\)个数字,这三个数字的和可能等于\(6\),也可能大于\(6\),
\(\therefore\)是否大于\(6\),需要取出数字才知道,
\(\therefore\)这三个数字的和大于\(6\)”这一事件是随机事件,
故选\(C\). -
【答案】\(C\)
【解析】(1)将一枚均匀的硬币抛\(2\)次,记事件\(A\):两次出现正面;事件\(B\):只有一次出现正面,事件\(A\) ,\(B\)不可能同时发生,故是互斥事件;
(2)某人射击一次,记事件\(A\):中靶,事件\(B\):射中9环,事件\(A\) ,\(B\)可能同时发生,故不是互斥事件
(3)某人射击一次,记事件\(A\):射中环数大于\(5\);事件\(B\):射中环数小于\(5\),事件\(A\) ,\(B\)不可能同时发生,故是互斥事件.
故选\(C\). -
【答案】\(C\)
【解析】从装有\(3\)个红球和\(2\)个白球的红袋内任取两个球,所有的情况有\(3\)种:“\(2\)个白球”、“一个白球和一个红球”、“\(2\)个红球”.
由于对立事件一定是互斥事件,且它们之中必然有一个发生而另一个不发生,
对于\(A\),至少有\(1\)个白球;都是白球,不是互斥事件.故不符合.
对于\(B\)两个白球;至少有一个红球,是互斥事件,但也是对立事件,故不符合.
对于\(C\)红球、白球各一个;都是白球是互斥事件,但不是对立事件不是互斥事件,故符合.
对于\(D\)红球、白球各一个;至少有一个白,不是互斥事件.故不符合.
故选:\(C\). -
【答案】\(A\)
【解析】因为\(M\)、\(N\)为互斥事件,如图:
 ,
,
无论哪种情况,\(\bar{M} \cup \bar{N}\)是必然事件.
故选:\(A\). -
【答案】\(A\)
【解析】 ,\(P(A \cup C)=P(\mathrm{~A})+P(\mathrm{C})=0.4+0.2=0.6\)
故选:\(A\) . -
【答案】\(C\)
【解析】先后抛掷两枚骰子,出现的点数共有:
\((1,1),(1,2),(1,3),(1,4),(1,5),(1,6)\),
\((2,1),(2,2),(2,3),(2,4),(2,5),(2,6)\),
\((3,1),(3,2),(3,3),(3,4),(3,5),(3,6)\),
\((4,1),(4,2),(4,3),(4,4),(4,5),(4,6)\),
\((5,1),(5,2),(5,3),(5,4),(5,5),(5,6)\),
\((6,1),(6,2),(6,3),(6,4),(6,5),(6,6)\),共\(36\)种,
其中点数之和是\(8\)的有\(5\)种,故\(P_1=\dfrac{5}{36}\);点数之和是\(7\)的有\(6\)种,故\(P_2=\dfrac{6}{36}\);
点数之和是\(6\)的有\(5\)种,故\(P_3=\dfrac{5}{36}\);故\(P_1=P_3<P_2\),
故选\(C\) -
【答案】\(D\)
【解析】分别从集合\(A\),\(B\)各取一个数,共有\(3×3=9\)组实数对,
若\(a=\dfrac{1}{2}\),则由\(a^k>1\)得\(k<0\),此时\(k=-1\),有\(1\)个,
若\(a=\dfrac{3}{2}\),则由\(a^k>1\)得\(k>0\),此时\(k=\dfrac{1}{2}\),\(2\),有\(2\)个,
若\(a=2\),则由\(a^k>1\)得\(k>0\),此时\(k=\dfrac{1}{2}\),\(2\),有\(2\)个,共有\(5\)个,
则对应的概率\(P=\dfrac{5}{9}\),
故选:\(D\). -
【答案】\(BC\)
【解析】抛掷两枚质地均匀的骰子,有如下随机事件:
\(A=\)“至少一枚点数为\(1\)”,\(B=\)“两枚骰子点数一奇一偶”,\(C=\)“两枚骰子点数之和为\(8\)”,\(D=\)“两枚骰子点数之和为偶数”.
对于\(A\) ,当 \(A=\{1\}\), \(B=\{2,3\}\) 时,\(A \subseteq B\) 不成立,故\(A\)错误;
对于\(B\), \(B\)和 \(D\)不能同时发生,也不能同时不发生,故 \(B\), \(D\)为对立事件,故\(B\)正确;
对于\(C\) ,\(A\) ,\(C\) 不能同时发生,是互斥事件,故\(C\) 正确;
对于\(D\) , \(A\)发生与否,对\(D\)的发生有影响, \(\therefore A\),\(D\) 不是相互独立事件,故\(D\)错误.
故选:\(BC\) . -
【答案】\(\dfrac{1}{3}\)
【解析】由于若设“出现\(3\)点”、“出现\(6\)点”分别为事件\(A\)、\(B\),
则事件\(A\) ,\(B\)为互斥事件,又由\(P(A)=P(B)=\dfrac{1}{6}\),
则出现点数为\(3\)的倍数的概率为\(P(A+B)=P(A)+P(B)=\dfrac{1}{3}\),
故答案为\(\dfrac{1}{3}\) -
【答案】\(0.2\)
【解析】由题意知,射手命中的概率为\(0.25+0.20+0.35=0.8\),
又由射手命中靶与不命中靶为对立事件,故不命中靶的概率是\(1-0.8=0.2\),
故答案为\(0.2\). -
【答案】\(\dfrac{3}{5}\)
【解析】\(∵\)事件\(A\) ,\(B\)互斥,\(P(AB)=0\),
\(∵\)它们都不发生的概率为\(\dfrac{2}{5}\),
\(\therefore [1-P(A)][1-P(B)]=\dfrac{2}{5}\),
\(\therefore 1-P(A)-P(B)+P(AB)=1-2P(B)-P(B)=\dfrac{2}{5}\),解得\(P(B)=\dfrac{1}{5}\),
\(\therefore P(A)=2P(B)=\dfrac{2}{5}\),
\(\therefore P (\bar{A})=1-A=1-\dfrac{2}{5}=\dfrac{3}{5}\). -
【答案】\(\dfrac{7}{27}\)
【解析】三辆车经过十字路口的情况有\(27\)种,
至少有两辆车向左转的情况数为\(7\)种,所以概率为:\(\dfrac{7}{27}\).故答案为:\(\dfrac{7}{27}\).

-
【答案】\(\dfrac{11}{36}\)
【解析】掷两次骰子,会有\(6 \times 6=36\)种可能.
点\(P(m, n)\)落在区域\(|x-2|+|y-2| \leqslant 2\)内,即\(|m-2|+|n-2| \leqslant 2\) ,则共有以下可能性.
① \((1,1),(1,2),(1,3)\);
② \((2,1),(2,2),(2,3),(2,4)\) ;
③ \((3,1),(3,2),(3,3)\) ;
④ \((4,2)\);
这\(11\)个点都满足 \(|m-2|+|n-2| \leqslant 2\) ,即所求概率为 \(P=\dfrac{11}{36}\). -
【答案】\(\dfrac{5}{36}\)
【解析】在网格中共有36个格点,而使得三角形面积为\(1\)的格点有\(5\)个
故使得三角形面积为\(1\)的概率为\(\dfrac{5}{36}\).

-
【答案】\(\dfrac{5}{6}\)
【解析】由于正方体骰子,六个面上分别刻有的\(1,2,3,4,5,6\)六个数字,
则事件\(A\)“朝上一面的点数是偶数”包括向上点数为\(2\),\(4\),\(6\)三种情况,
事件\(B\)“朝上一面的点数不超过\(4\)”包括向上点数为\(1\),\(2\),\(3\)三种情况,
故事件\(A\cup B\)包括向上点数为\(1,2,3,4,6\)五种情况
故\(P(A\cup B)=\dfrac{5}{6}\). -
【答案】\(\dfrac{4}{9}\)
【解析】(1)由题意知甲、乙乘坐地铁均不超过\(3\)站,前\(3\)站设为\(A_1, B_1, C_1\),
甲、乙两人共有\(\left(\mathrm{A}_1, \mathrm{~A}_1\right),\left(\mathrm{A}_1, \mathrm{~B}_1\right),\left(\mathrm{A}_1, \mathrm{C}_1\right),\left(\mathrm{B}_1, \mathrm{~A}_1\right),\left(\mathrm{B}_1, \mathrm{~B}_1\right)\),
\(\left(\mathrm{B}_1, \mathrm{C}_1\right),\left(\mathrm{C}_1, \mathrm{~A}_1\right),\left(\mathrm{C}_1, \mathrm{~B}_1\right),\left(\mathrm{C}_1, \mathrm{C}_1\right)\),\(9\)种下车方案.
(2)设\(9\)站分别为\(A_1, B_1, C_1, A_2, B_2, C_2, A_3, B_3, C_3\),
因为甲、乙两人共付费\(4\)元,共有甲付\(1\)元,乙付\(3\)元;甲付\(3\)元,乙付\(1\)元;甲付\(2\)元,乙付\(2\)元三类情况.
由(1)可知每类情况中有\(9\)种方案,
所以甲、乙两人共付费\(4\)元共有\(27\)种方案.
而甲比乙先到达目的地的方案有:
\(\left(\mathrm{A}_1, \mathrm{~A}_3\right),\left(\mathrm{A}_1, \mathrm{~B}_3\right),\left(\mathrm{A}_1, \mathrm{C}_3\right),\left(\mathrm{B}_1, \mathrm{~A}_3\right),\left(\mathrm{B}_1, \mathrm{~B}_3\right),\left(\mathrm{B}_1, \mathrm{C}_3\right),\left(\mathrm{C}_1, \mathrm{~A}_3\right)\),
\(\left(\mathrm{C}_1, \mathrm{~B}_3\right),\left(\mathrm{C}_1, \mathrm{C}_3\right),\left(\mathrm{A}_2, \mathrm{~B}_2\right),\left(\mathrm{A}_2, \mathrm{C}_2\right),\left(\mathrm{B}_2, \mathrm{C}_2\right)\),共\(12\)种,
故所求概率为\(\dfrac{12}{27}=\dfrac{4}{9}\).
所以甲比乙先到达目的地的概率为\(\dfrac{4}{9}\).