\({\color{Red}{欢迎到学科网下载资料学习 }}\)
[ 【基础过关系列】高一数学同步精品讲义与分层练习(人教A版2019)]
(https://www.zxxk.com/docpack/2921718.html)
\({\color{Red}{ 跟贵哥学数学,so \quad easy!}}\)
必修第二册同步巩固,难度2颗星!
基础知识
圆柱
(1) 侧面积:\(S=2πrh\)
(2) 全面积:\(S=2πrh+2πr^2\)
(3) 体积:\(V=Sh=πr^2 h\) (其中\(r\)为底圆的半径,\(h\)为圆柱的高)
解释
圆柱的侧面展开图是一个长方形.

圆锥
(1) 圆锥侧面积:\(S=πrl\)
(2) 圆锥全面积:\(S=πr(r+l)\)(其中\(r\)为底圆的半径,\(l\)为圆锥母线)
(3) 圆锥体积:\(V=\dfrac{1}{3} Sh=\dfrac{1}{3} πr^2 h\) (其中\(r\)为底圆的半径,\(h\)为圆锥的高)

解释
圆锥侧面的展开图是扇形,扇形的弧长等于圆锥底圆周长.
圆锥的高为\(SO\).
圆台
圆台表面积 \(S=\pi\left(r^{\prime 2}+r^{\prime 2}+r^{\prime} l+r l\right)\)
其中\(r'\)是上底面圆的半径,\(r\)是下底面圆的半径,\(l\)是母线的长度.
圆台体积\(V_{\text {圆台 }}=\dfrac{1}{3} \pi h\left(r^{\prime 2}+r^{\prime} r+r^2\right)\)(\(r'\),\(r\)分别是上、下底面半径,\(h\)是高).

解释
① 圆台侧面的展开图是圆环的一部分;圆台的高\(h=OO'\).
② 圆台体积 \(V_{\text {圆台 }}=\dfrac{1}{3}\left(S_{\text {上圆 }}+\sqrt{S_{\text {上圆 }} S_{\text {下圆 }}}+S_{\text {下圆 }}\right) h=\dfrac{1}{3}\left(\pi r^{\prime 2}+\pi r^{\prime} r+\pi r^2\right) h\)
\(=\dfrac{1}{3} \pi h\left(r^{\prime 2}+r^{\prime} r+r^2\right)\).
球体
面积\(S=4 \pi R^2\),体积 \(V=\dfrac{4}{3} \pi R^3\)(其中\(R\)为球的半径)
解释
球体的表面积公式在高中不作推导要求,体积公式可类比利用圆周长求圆面积的方法,了解到“球体体积等于无穷个小椎体的和”.
基本方法
【题型1】 圆柱、圆锥、圆台的表面积
【典题1】已知某圆锥的底面半径为\(1\),高为\(\sqrt{3}\),则它的侧面积与底面积之比为( )
A.\(\dfrac{1}{2}\) \(\qquad \qquad \qquad \qquad\) B.\(1\) \(\qquad \qquad \qquad \qquad\) C.\(2\) \(\qquad \qquad \qquad \qquad\) D.\(4\)
解析 圆锥的侧面积为: \(S_1=\pi r l=\pi r \sqrt{r^2+h^2}=2 \pi\),
圆锥的底面积为: \(S_2=\pi r^2=\pi\),
所以侧面积与底面积之比为\(2\).
故选:\(C\).
【典题2】圆台的上、下底面半径分别是\(10 cm\)和\(20 cm\),它的侧面展开图的扇环的圆心角是\(180^{\circ}\),那么圆台的表面积是多少?
解析 如图所示,设圆台的上底面周长为\(c\),因为扇环的圆心角是\(180^{\circ}\),

故\(c=π·SA=2π×10\),\(\therefore SA=20\).同理可得\(SB=40\).
\(\therefore AB=SB-SA=20\).
\(\therefore S_{\text {表面积 }}=S_{\text {侧 }}+S_{\text {上 }}+S_{\text {下 }}=\pi\left(r_1+r_2\right) \cdot A \cdot B+\pi r_1^2+\pi r_2^2\)
\(=π(10+20)×20+π×102+π×202=1100π(cm^2)\)
故圆台的表面积为\(1100π cm^2\).
【巩固练习】
1.若一个圆柱的轴截面是面积为\(8\)的正方形,则这个圆柱的侧面积为( )
A.\(4\pi\) \(\qquad \qquad \qquad \qquad\) B.\(8\pi\) \(\qquad \qquad \qquad \qquad\) C.\(4\sqrt{2} \pi\) \(\qquad \qquad \qquad \qquad\) D.\(12\pi\)
2.已知圆锥的轴截面是腰长为\(10\)的等腰三角形,且该三角形底角的正弦值为\(\dfrac{3}{5}\),则该圆锥的底面积与表面积之比为( )
A.\(\dfrac{1}{3}\) \(\qquad \qquad \qquad \qquad\) B.\(\dfrac{5}{9}\) \(\qquad \qquad \qquad \qquad\) C.\(\dfrac{4}{9}\) \(\qquad \qquad \qquad \qquad\) D.\(\dfrac{7}{9}\)
3.一个圆台上、下底面半径分别为\(r\)、\(R\),高为\(h\),若其侧面积等于两底面面积之和,则下列关系正确的是( )
A. \(\dfrac{2}{h}=\dfrac{1}{R}+\dfrac{1}{r}\) \(\qquad \qquad\) B. \(\dfrac{1}{h}=\dfrac{1}{R}+\dfrac{1}{r}\) \(\qquad \qquad\) C. \(\dfrac{1}{r}=\dfrac{1}{R}+\dfrac{1}{h}\) \(\qquad \qquad\) D. \(\dfrac{2}{R}=\dfrac{1}{r}+\dfrac{1}{h}\)
参考答案
- 答案 \(B\)
解析圆柱的轴截面是面积为\(8\)的正方形,则这个圆柱的高是 \(h=\sqrt{8}=2 \sqrt{2}\);
底面圆半径为\(r=\sqrt{2}\),
\(\therefore\)圆柱的侧面积为 \(S_{\text {侧面 }}=2 \pi r h=2 \pi \times \sqrt{2} \times 2 \sqrt{2}=8 \pi\).
故选:\(B\). - 答案 \(C\)
解析 设圆锥的底面半径为\(r\),
\(\because\)圆锥的轴截面是腰长为\(10\)的等腰三角形,且该三角形底角的正弦值为 \(\dfrac{3}{5}\),
则该圆锥的高为\(6\),底面半径为\(8\),
\(\therefore\)圆锥的底面积为:\(\pi×8^2=64\pi\),
圆锥的表面积为:\(\pi×8×10+\pi×8^2=144\pi\),
\(\therefore\)该圆锥的底面积与表面积之比为\(64\pi:144\pi=4:9\),
故答案为:\(C\). - 答案 \(A\)
解析 设圆台的母线长为\(l\),
根据题意可得圆台的上底面面积为\(S_{\text {上 }}=\pi r^2\),圆台的下底面面积为 \(S_{\text {下 }}=\pi R^2\),
\(\because\)圆台的侧面面积等于两底面面积之和,
\(\therefore\) 侧面积 \(S_{\text {侧 }}=\pi\left(r^2+R^2\right)=\pi(r+R) l\),解之得 \(l=\dfrac{r^2+R^2}{r+R}\),
\(\because l=\sqrt{h^2+(R-r)^2}\), \(\therefore \dfrac{r^2+R^2}{r+R}=\sqrt{h^2+(R-r)^2}\),
\(\therefore\left(\dfrac{r^2+R^2}{r+R}\right)^2=h^2+(R-r)^2\), \(\therefore \dfrac{2}{h}=\dfrac{1}{R}+\dfrac{1}{r}\).
故选 \(A\).
【题型2】 圆柱、圆锥、圆台的体积
【典题1】 已知一个圆锥的底面积为\(\pi\),侧面积为\(2\pi\),则该圆锥的体积为 ( )
A.\(8\sqrt{6} \pi\) \(\qquad \qquad \qquad \qquad\) B.\(4\sqrt{6} \pi\) \(\qquad \qquad \qquad \qquad\) C.\(\dfrac{\sqrt{3} \pi}{3}\) \(\qquad \qquad \qquad \qquad\) D. \(\dfrac{2 \sqrt{2} \pi}{3}\)
解析 设圆锥的底面半径、高、母线长分别为\(r\),\(h\),\(l\),
则 \(\left\{\begin{array}{l}
\pi r^2=\pi \\
\pi r l=2 \pi
\end{array}\right.\),解得 \(\left\{\begin{array}{l}
r=1 \\
l=2
\end{array}\right.\),所以\(h=\sqrt{3}\).
圆锥的体积 \(V=\dfrac{1}{3} S h=\dfrac{1}{3} \times \pi \times 1^2 \times \sqrt{3}=\dfrac{\sqrt{3} \pi}{3}\),
故选:\(C\).
【典题2】如图,已知梯形\(ABCD\)中,\(AD∥BC\),\(∠ABC=90^{\circ}\),\(AD=a\),\(BC=2a\),\(∠DCB=60^{\circ}\),若在平面\(ABCD\)内过点\(C\)作\(l⊥CB\),以\(l\)为轴旋转一周.求旋转体的表面积和体积.

解析 如图,在梯形\(ABCD\)中,\(∠ABC=90^{\circ}\),\(AD∥BC\),\(AD=a\),\(BC=2a\),\(∠DCB=60^{\circ}\),
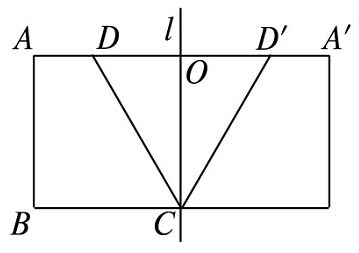
\(\therefore C D=\dfrac{B C-A D}{\cos 60^{\circ}}=2 a\), \(A B=C D \sin 60^{\circ}=\sqrt{3} a\),
\(\therefore DD'=AA'-2AD=2BC-2AD=2a\),\(\therefore DO=\dfrac{1}{2} DD'=a\).
由于以\(l\)为轴将梯形\(ABCD\)旋转一周后形成的几何体 为圆柱中挖去一个倒放的与圆柱等高的圆锥.
由上述计算知,圆柱母线长\(\sqrt{3} a\),底面半径\(2a\),圆锥的母线长\(2a\),底面半径\(a\).
\(\therefore\)圆柱的侧面积\(S_1=2 \pi \cdot 2 a \cdot \sqrt{3} a=4 \sqrt{3} \pi a^2\),圆锥的侧面积 \(S_2=\pi \cdot a \cdot 2 a=2 \pi a^2\),
圆柱的底面积\(S_3=\pi(2 a)^2=4 \pi a^2\),圆锥的底面积 \(S_4=\pi a^2\),
\(\therefore\)组合体上底面积 \(S_5=S_3-S_4=3 \pi a^2\),
\(\therefore\) 旋转体的表面积 \(S=S_1+S_2+S_3+S_5=(4 \sqrt{3}+9) \pi a^2\).
又由题意知形成的几何体的体积为一个圆柱的体积减去一个圆锥的体积.
\(V_{\text {柱 }}=S h=\pi \cdot(2 a)^2 \cdot \sqrt{3} a=4 \sqrt{3} \pi a^3\),\(V_{\text {锥 }}=\dfrac{1}{3} S^{\prime} h=\dfrac{1}{3} \cdot \pi \cdot a^2 \cdot \sqrt{3} a=\dfrac{\sqrt{3}}{3} \pi a^3\),
\(\therefore V=V_{\text {柱 }}-V_{\text {雉 }}=4 \sqrt{3} \pi a^3-\dfrac{\sqrt{3}}{3} \pi a^3=\dfrac{11 \sqrt{3}}{3} \pi a^3 \text {. }\).
【巩固练习】
1.若一个圆锥的轴截面是边长为\(2\)的正三角形,则这个圆锥的体积为( )
A. \(\dfrac{\sqrt{3}}{3} \pi\) \(\qquad \qquad \qquad \qquad\) B.\(\dfrac{\sqrt{3}}{2} \pi\) \(\qquad \qquad \qquad \qquad\) C.\(\sqrt{2} \pi\) \(\qquad \qquad \qquad \qquad\) D.\(2\pi\)
2.一个圆柱的侧面展开图是一个面积为\(16 \pi^2\)的正方形,则这个圆柱的体积为 ( )
A.\(16\pi\) \(\qquad \qquad \qquad \qquad\) B.\(4\pi\) \(\qquad \qquad \qquad \qquad\) C.\(16 \pi^2\) \(\qquad \qquad \qquad \qquad\) D.\(8\pi^2\)
3.陀螺是中国民间最早的娱乐工具之一,也称陀罗.图\(1\)是一种木陀螺,可近似地看作是一个圆锥和一个圆柱的组合体,其直观图如图\(2\)所示,其中\(B\),\(C\)分别是上、下底面圆的圆心,且\(AC=3AB\),则该陀螺下半部分的圆柱与上半部分的圆锥的体积的比值是( )

A.\(2\) \(\qquad \qquad \qquad \qquad\) B.\(3\) \(\qquad \qquad \qquad \qquad\) C.\(4\) \(\qquad \qquad \qquad \qquad\) D.\(6\)
4.若某圆台的上底面半径为\(2\),下底面半径为\(4\),高为\(3\),则该圆台的体积为( )
A. \(\dfrac{28 \pi}{3}\) \(\qquad \qquad \qquad \qquad\) B.\(20\pi\) \(\qquad \qquad \qquad \qquad\) C. \(28π\) \(\qquad \qquad \qquad \qquad\) D.\(32\pi\)
5.如图①,一个圆锥形容器的高为\(a\),内装有一定量的水.如果将容器倒置,这时所形成的圆锥的高恰为\(\dfrac{a}{2}\)(如图②),则图①中的水面高度为 ( )

A.\(\dfrac{a}{2}\) \(\qquad \qquad \qquad \qquad\) B.\(\dfrac{a}{3}\) \(\qquad \qquad \qquad \qquad\) C. \(\dfrac{\sqrt[3]{7}}{2} a\) \(\qquad \qquad \qquad \qquad\) D. \(\left(1-\dfrac{\sqrt[3]{7}}{2}\right) a\)
参考答案
-
答案 \(A\)
解析 \(\because\) 圆锥的轴截面是正三角形\(ABC\),边长等于\(2\),
\(\therefore\)圆锥的高\(A O=\dfrac{\sqrt{3}}{2} \times 2=\sqrt{3}\),底面半径\(r=\dfrac{1}{2}×2=1\),
因此,该圆锥的体积 \(V=\dfrac{1}{3} \pi r^2 \cdot A O=\dfrac{1}{3} \pi \times 1^2 \times \sqrt{3}=\dfrac{\sqrt{3}}{3} \pi\),
故选:\(A\).

-
答案 \(C\)
解析 设圆柱的底面半径为\(r\),高为\(h\),因为圆柱的侧面展开图是一个面积为\(16 \pi^2\)的正方形,
所以\(h=2 \pi r\), \(h^2=16 \pi^2\),所以\(h=4\pi\),\(r=2\),
所以圆柱的体积为 \(\pi r^2 \cdot h=16 \pi^2\).
故选:\(C\). -
答案 \(D\)
解析 设圆锥的底面半径为\(r\),高为\(h\),则圆柱的底面半径为\(r\),高为\(BC=2h\),
所以圆柱的体积是 \(V_{\text {圆柱 }}=\pi r^2 \cdot 2 h=2 \pi r^2 h\),
圆锥的体积是 \(V_{\text {圆雉 }}=\dfrac{1}{3} \pi r^2 h\),
所以 \(\dfrac{V_{\text {圆柱 }}}{V_{\text {圆雉 }}}=\dfrac{2 \pi r^2 h}{\dfrac{1}{3} \pi r^2 h}=6\).
故选:\(D\). -
答案 \(C\)
解析 由公式$V=\dfrac{1}{3}\left(S_{\text {上 }}+S_{\text {下 }}+\sqrt{S_{\text {上 }} S_{\text {下 }}}\right) h $,
可知:该圆台的体积为 \(V=\dfrac{1}{3}\left(\pi \times 2^2+\pi \times 4^2+\sqrt{\pi \times 2^2 \times \pi \times 4^2}\right) \times 3=28 \pi\),
故选:\(C\). -
答案 \(D\)
解析 令圆锥倒置时水的体积为\(V'\),圆锥体积为\(V\),
则 \(\dfrac{V^{\prime}}{V}=\left(\dfrac{a}{2}\right)^3 \div a^3=\dfrac{1}{8}\), \(\therefore \dfrac{V_{\text {空 }}}{V_{\text {锥 }}}=\dfrac{7}{8}\),倒置后 \(V_{\text {水 }}=\dfrac{1}{8} V\),
设此时水高为\(h\),则\(h^3 a^3=\dfrac{7}{8}\), \(\therefore h=\left(1-\dfrac{\sqrt[3]{7}}{2}\right) a\).
故原来水面的高度为\(\left(1-\dfrac{\sqrt[3]{7}}{2}\right) a\).
故选 \(D\).
【题型3】球的表面积和体积
【典题1】 (1)已知球的直径为\(8 cm\),求它的表面积和体积;
(2)已知球的表面积为\(144\pi\),求它的体积;
(3)已知球的体积为\(\dfrac{500}{3} \pi\),求它的表面积.
解析 (1)\(\because\)球的直径为\(8 cm\),
\(\therefore\) 半径\(R=4 cm\).
\(\therefore\)表面积\(S_{\text {球 }}=4 \pi R^2=64 \pi\left(\mathrm{cm}^2\right)\),体积 \(V_{\text {球 }}=\dfrac{4}{3} \pi R^3=\dfrac{256}{3} \pi\left(\mathrm{cm}^3\right)\).
(2) \(\because S_{\text {球 }}=4 \pi R^2=144 \pi\),\(\therefore R=6\).
\(\therefore V_{\text {球 }}=\dfrac{4}{3} \pi R^3=\dfrac{4}{3} \pi \times 6^3=288 \pi\).
(3) \(\because V_{\text {球 }}=\dfrac{4}{3} \pi R^3=\dfrac{500 \pi}{3}\),\(\therefore R=5\).
.
【巩固练习】
1.在球面上有四个点\(A\),\(B\),\(C\),\(P\),且\(PA\),\(PB\),\(PC\)两两垂直,\(PA=a\),\(PB=\sqrt{2} a\),\(PC=a\).则球的体积是\(\underline{\quad \quad}\).
2.如图所示,已知一个半径为\(6\)的半圆面剪去了一个三角形\(ABC\),将剩余部分绕着直径\(AB\)所在直线旋转一周得到一个几何体,其中点\(C\)为半圆弧的中点,求该几何体的表面积和体积.

3.已知半径为\(5\)的球的两个平行截面圆的周长分别为\(6\pi\)和\(8\pi\),求这两个截面间的距离.
参考答案
-
答案 \(\dfrac{4}{3} \pi a^3\)
解析 以\(PA\),\(PB\),\(PC\)为棱作一长方体,则该长方体内接于球.
设长方体的对角线长为\(l\),球半径为\(R\),则 \(l=\sqrt{a^2+(\sqrt{2} a)^2+a^2}=2 a\).
所以\(R=a\).所以 \(V_{\text {球 }}=\dfrac{4}{3} \pi a^3\). -
答案 \(144\pi\)
解析 由题意可知,该几何体为球内部挖去两个相同的圆锥,如图所示:

圆锥的半径为\(6\),高为\(6\),母线长为\(6\sqrt{2}\),
所以圆锥的表面积\(S=\pi×6×6\sqrt{2}=36\sqrt{2} \pi\),圆锥的体积 \(V=\dfrac{1}{3} \times \pi \times 6^2 \times 6=72 \pi\),
所以该几何体的表面积 \(S^{\prime}=S_{\text {球 }}+2 S=4 \pi \times 6^2+2 \times 36 \sqrt{2} \pi=(144+72 \sqrt{2}) \pi\),
该几何体的体积\(V=V_{\text {球 }}-2 V=\dfrac{4}{3} \pi \times 6^3-2 \times 72 \pi=144 \pi\). -
答案 \(1\)或\(7\)
解析 当两个截面在球心同一侧时,其轴截面如图甲.由题意知\(O_1 A=3\),\(O_2 B=4\),
又\(OA=OB=5\),由勾股定理得\(OO_1=4\),\(OO_2=3\).
\(\therefore O_1 O_2=1\).
当两个截面在球心两侧时,其轴截面如图乙.
同理可得\(OO_1=4\),\(OO_2=3\),
\(\therefore O_1 O_2=7\).
\(\therefore\)这两个截面间的距离为\(1\)或\(7\).

分层练习
【A组---基础题】
1.圆柱的母线长为\(5cm\),底面半径为\(2cm\),则圆柱的侧面积为( )
A.\(20\pi cm^2\) \(\qquad \qquad \qquad \qquad\) B.\(10\pi cm^2\) \(\qquad \qquad \qquad \qquad\) C.\(28\pi cm^2\) \(\qquad \qquad \qquad \qquad\) D.\(14\pi cm^2\)
2.若一个圆锥的母线长为\(4\),且其侧面积为其轴截面面积的\(4\)倍,则该圆锥的高为( )
A.\(\pi\) \(\qquad \qquad \qquad \qquad\) B. \(\dfrac{3 \pi}{2}\) \(\qquad \qquad \qquad \qquad\) C. \(\dfrac{2 \pi}{3}\) \(\qquad \qquad \qquad \qquad\) D.\(\dfrac{ \pi}{2}\)
3.如图,一个圆锥形的空杯子上面放着一个半径为\(4.5cm\)的半球形的冰淇淋,若冰淇淋融化后正好盛满杯子,则杯子的高\(h=\)( )

A.\(9cm\) \(\qquad \qquad \qquad \qquad\) B.\(6cm\) \(\qquad \qquad \qquad \qquad\) C.\(3cm\) \(\qquad \qquad \qquad \qquad\) D.\(4.5cm\)
4.已知圆台下底面的半径为\(2\),高为\(2\),母线长为\(\sqrt{5}\),则这个圆台的体积为 ( )
A. \(\dfrac{14}{3} \pi\) \(\qquad \qquad \qquad \qquad\) B. \(\dfrac{7}{2} \pi\) \(\qquad \qquad \qquad \qquad\) C. \(\dfrac{14}{5} \pi\) \(\qquad \qquad \qquad \qquad\)D. \(\dfrac{7}{3} \pi\)
5.如图一个圆柱和一个圆锥的底面直径和它们的高都与一个球的直径相等,这时圆柱、圆锥、球的表面积之比为( )

A.\(6: (\sqrt{5}+1):4\) \(\qquad \qquad\) B.\(6:\sqrt{5}: 4\) \(\qquad \qquad\)C.\(5:(\sqrt{5}+1):4\) \(\qquad \qquad\) D.\(5:\sqrt{5}: 4\)
6.正方形\(ABCD\)被对角线\(BD\)和以\(A\)为圆心,\(AB\)为半径的圆弧 \(\widehat{D B}\)分成三部分,绕\(AD\)旋转,所得旋转体的体积\(V_1\) 、\(V_2\)、\(V_3\)之比是( )

A.\(2:1:1\) \(\qquad \qquad \qquad\) B.\(1:2:1\) \(\qquad \qquad \qquad\) C.\(1:1:1\) \(\qquad \qquad \qquad\) D.\(2:2:1\)
7.如图,某粮仓(粮仓的底部位于地面上)是由圆柱和圆锥构成的,若圆柱的高是圆锥高的\(2\)倍,且圆锥的母线长是\(4\),侧面积是\(4\pi\),则这样一个粮仓的容积为\(\underline{\quad \quad}\).

8.如图,已知圆锥的高是底面半径的\(2\)倍,侧面积为\(\pi\),若正方形\(ABCD\)内接于底面圆\(O\),则四棱锥\(P﹣ABCD\)侧面积为\(\underline{\quad \quad}\).

9.一个底面半径为\(2\),高为\(4\)的圆锥中有一个内接圆柱,该圆柱侧面积的最大值为\(\underline{\quad \quad}\).
10.已知过球面上三点\(A\),\(B\),\(C\)的截面到球心的距离等于球半径的 \(\dfrac{\sqrt{3}}{2}\)倍,且\(AC=8\),\(BC=6\),\(AB=10\),求球 的表面积与球的体积.
参考答案
-
答案 \(A\)
解析 圆柱的母线长为\(5cm\),底面半径为\(2cm\),
则圆柱的侧面积为 \(S_{\text {侧 }}=2 \pi \times 2 \times 5=20 \pi\left(\mathrm{cm}^2\right)\).
故选:\(A\). -
答案 \(A\)
解析 设圆锥的底面圆半径为\(r\),高为\(h\);
由圆锥的母线长为\(4\),所以圆锥的侧面积为\(\pi r\cdot 4=4\pi r\);
又圆锥的轴截面面积为\(\dfrac{1}{2}\cdot 2r\cdot h=rh\),
所以\(4\pi r=4rh\),解得\(h=\pi\);
所以该圆锥的高为\(\pi\).
故选:\(A\). -
答案 \(A\)
解析 由题意可得, \(\dfrac{1}{2} \times \dfrac{4 \pi}{3} \times 4.5^3=\dfrac{1}{3} \times \pi \times 4.5^2 \times h\),解得\(h=9\).故选:\(A\). -
答案 \(A\)
解析 如图所示,

\(AA_1=\sqrt{5}\),\(OA=2\),\(O_1 O=2\),
过\(A_1\)作\(A_1 B⊥OA\),垂足为\(B\),则\(A_1 B=O_1 O=2\),
\(A B=O A-O B=O A-O_1 A_1=\sqrt{(\sqrt{5})^2-2^2}=1\),
所以圆台的上底面半径为\(O_1 A_1=1\);
所以圆台的体积为 \(V=\dfrac{1}{3} \pi\left(1^2+1 \times 2+2^2\right) \times 2=\dfrac{14 \pi}{3}\left(\mathrm{~cm}^3\right)\).
故选:\(A\). -
答案 \(A\)
解析 依题意,设球的半径为\(r\),则圆柱的底面半径为\(r\),母线长\(l_柱=2r\),
所以圆柱的表面积\(S_{\text {柱 }}=2 \pi r\left(r+l_{\text {柱 }}\right)=6 \pi r^2\),
圆锥的底面半径为\(r\),高为\(2r\),所以圆锥的母线长 \(l_{\text {锥 }}=\sqrt{r^2+(2 r)^2}=\sqrt{5} r\),
所以圆锥的表面积\(S_{\text {锥 }}=\pi r\left(r+l_{\text {锥 }}\right)=\pi r(r+\sqrt{5} r)=\pi r^2(1+\sqrt{5})\),
而球的表面积 \(S_{\text {球 }}=4 \pi r^2\),
所以圆柱、圆锥、球的表面积之比为 \(6 \pi r^2: \pi r^2(1+\sqrt{5}): 4 \pi r^2=6:(1+\sqrt{5}): 4\).
故选 \(A\). -
答案 \(C\)
解析 设正方形\(ABCD\)的边长为\(1\),可得
图\(1\)旋转所得旋转体为以\(AD\)为轴的圆锥体,高\(AD=1\)且底面半径\(r=1\),
\(\therefore\)该圆锥的体积为 \(V_1=\dfrac{1}{3} \pi \times A B^2 \times A D=\dfrac{1}{3} \pi\);
图\(2\)旋转所得旋转体,是以\(AD\)为半径的一个半球,减去图\(1\)旋转所得圆锥体而形成,
\(\therefore\)该圆锥的体积为 \(V_2=\dfrac{1}{2} \times \dfrac{4}{3} \pi \times A D^2-V_1=\dfrac{1}{3} \pi\);
图\(3\)旋转所得旋转体,是以\(AD\)为轴的圆柱体,减去图2旋转所得半球而形成,
\(\therefore\)该圆锥的体积为 \(V_3=\pi \times A B^2 \times A D-V_{\text {半球 }}=\pi-\dfrac{2}{3} \pi=\dfrac{1}{3} \pi\);
综上所述 \(V_1=V_2=V_3=\dfrac{1}{3} \pi\) ,
由此可得图中\(1\)、\(2\)、\(3\)三部分旋转所得旋转体的体积之比为\(1:1:1\).
故选 \(C\). -
答案 \(\dfrac{7}{3} \sqrt{15} \pi\)
解析 设圆锥的母线为\(l\),底面半径为\(r\),高为\(h\),
所以\(\pi rl=4\pi\),解得\(r=1\), \(h=\sqrt{4^2-1^2}=\sqrt{15}\);
所以圆柱的高为 \(2 \sqrt{15}\),
所以这样一个粮仓的容积为 \(\dfrac{1}{3} \times \pi \times 1^2 \times \sqrt{15}+\pi \times 1^2 \times 2 \sqrt{15}=\dfrac{7}{3} \sqrt{15} \pi\). -
答案 \(\dfrac{6 \sqrt{5}}{5}\)
解析 \(\because\)圆锥的高是底面半径的\(2\)倍,侧面积为\(\pi\),
\(\therefore\)设底面半径为\(r\),则高为\(2r\),母线长 \(l=\sqrt{r^2+4 r^2}=\sqrt{5} \mathrm{r}\),
\(\therefore\)圆锥的侧面积\(S=\pi rl=\pi ×r×\sqrt{5} r=\pi\),
解得 \(r=\sqrt{\dfrac{1}{\sqrt{5}}}\), \(l=\sqrt{5} \times \sqrt{\dfrac{1}{\sqrt{5}}}=\sqrt[4]{5}\),
\(\because\)正方形\(ABCD\)内接于底面圆\(O\),
\(\therefore AB=\sqrt{2} r\),
\(\therefore\)四棱锥\(P﹣ABCD\)侧面积为: \(S=4 S_{\triangle P A B}=4 \times \dfrac{1}{2} \times A B \times \sqrt{P A^2-\left(\dfrac{A B}{2}\right)^2}\)
\(=2 \times \sqrt{2} r \times \sqrt{5 r^2-\dfrac{1}{2} r^2}=6 r^2=6 \times \dfrac{1}{\sqrt{5}}=\dfrac{6 \sqrt{5}}{5}\). -
答案 \(4\pi\)
解析 圆锥的底面半径为\(2\),高为\(4\),
\(\therefore\)内接圆柱的底面半径为\(x\)时,它的上底面截圆锥得小圆锥的高为\(2x\)
因此,内接圆柱的高\(h=4-2x\);
\(\therefore\) 圆柱的侧面积为:\(S=2 \pi x(4-2 x)=4 \pi (2 x-x^2)\),\((0<x<2)\),
令\(t=2 x-x^2\),当\(x=1\)时 \(t_{\max }=1\);
所以当\(x=1\)时, \(S_{\max }=4 \pi\) .
即圆柱的底面半径为\(1\)时,圆柱的侧面积最大,最大值为\(4\pi\) .

-
答案 球的表面积\(400\pi\) ,球的体积\(\dfrac{4000}{3} \pi\).
解析 如图,设球的半径为\(R\),球心为\(O\),截面圆心为\(O_1\),则 \(O O_1=\dfrac{\sqrt{3}}{2} R\).在\(△ABC\)中,

\(\because A C^2+B C^2=A B^2\),\(\therefore ∠ACB=90^{\circ}\),
\(\therefore O_1\) 是\(AB\)的中点,即\(O_1 B=5\).
又 \(O O_1^2+O_1 A^2=O A^2\),
\(\therefore\left(\dfrac{\sqrt{3}}{2} R\right)^2+5^2=R^2\),
\(\therefore R^2=100\),\(R=10\).
\(\therefore\)球的表面积 \(S_{\text {球 }}=4 \pi R^2=4 \pi \times 10^2=400 \pi\),
球的体积 \(V_{\text {球 }}=\dfrac{4}{3} \pi R^3=\dfrac{4}{3} \pi \times 10^3=\dfrac{4000}{3} \pi\).
【B组---提高题】
1.已知四面体\(ABCD\)的棱长满足\(AB=AC=BD=CD=2\),\(BC=AD=1\),现将四面体\(ABCD\)放入一个主视图为等边三角形的圆锥中,使得四面体\(ABCD\)可以在圆锥中任意转动,则圆锥侧面积的最小值为\(\underline{\quad \quad}\).
2.已知球的直径\(SC=4\),\(A\),\(B\)是该球球面上的两点,\(AB=2\),\(∠ ASC=∠BSC=45^{\circ}\),则棱锥\(S-ABC\)的体积\(V=\) \(\underline{\quad \quad}\) .
3.已知球的两平行截面的面积为\(5\pi\)和\(8\pi\),它们位于球心的同一侧,且相距为\(1\),求这个球的表面积和体积.
参考答案
-
答案 \(\dfrac{27 \pi}{4}\)
解析 因为四面体\(ABCD\)的棱长满足\(AB=AC=BD=CD=2\),\(BC=AD=1\),
所以可以把其放到长宽高分别为\(a\),\(b\),\(c\)的长方体中,四面体的棱长是长方体的面对角线,
\(\therefore a^2+b^2=2^2\)① ,\(b^2+c^2=2^2\)②; \(c^2+a^2=1^2\)③
故四面体的外接球半径\(R\)满足: \(8 R^2=2^2+2^2+1^2=9\);
\(\therefore R^2=\dfrac{9}{8}\).
\(\because\)四面体\(ABCD\)放入一个主视图为等边三角形的圆锥中,
使得四面体\(ABCD\)可以在圆锥中任意转动,
要想圆锥的侧面积最小;
故需满足四面体的外接球恰好是圆锥的内切球;
作圆锥的轴截面,如图:设\(BE=r\),则\(AB=2r\),\(AE=\sqrt{3} r\);
可得: \(O B^2=O E^2+E B^2\);
\(\therefore R^2=(\sqrt{3} r-R)^2+r^2 \Rightarrow r=\sqrt{3} R\);
故圆锥侧面积的最小值为: \(\pi r l=2 \pi r^2=2 \pi \cdot 3 R^2=\dfrac{27 \pi}{4}\).
故答案为: \(\dfrac{27 \pi}{4}\).

-
答案 \(\dfrac{4 \sqrt{3}}{3}\)
解析 由题可知\(AB\)一定在与直径\(SC\)垂直的小圆面上,作过\(AB\)的小圆交直径\(SC\)于\(D\),
如图所示,设\(SD=x\),则\(DC=4-x\),
此时所求棱锥即分割成两个棱锥\(SABD\)和\(CAB D\),在\(△SAD\)和\(△SBD\)中,
由已知条件可得\(AD=BD=x\),
又因为\(SC\)为直径,所以\(∠SBC=∠SAC=90^{\circ}\),
所以\(\angle D B C=\angle D A C=45^{\circ}\),所以在\(△BDC\)中,\(BD=4-x\),
所以\(x=4-x\),解得\(x=2\),所以\(AD=BD=2\),
所以 \(\triangle A B D\)为正三角形,所以 \(V=\dfrac{1}{3} S_{\triangle A B D} \times 4=\dfrac{4 \sqrt{3}}{3}\).

-
答案 球的表面积\(36\pi\),球的体积\(36\pi\)
解析 如图是球的轴截面.

设以\(r_1\)为半径的截面面积为\(5\pi\),以\(r_2\)为半径的截面面积为\(8\pi\),\(O_1 O_2=1\),球的半径为\(R\),
则\(\pi r_1^2=5 \pi\),\(\pi r_2^2=8 \pi\),
\(\therefore r_1^2=5\),\(r_2^2=8\).
\(\therefore O O_1=\sqrt{R^2-r_1^2}=\sqrt{R^2-5}\),\(O O_2=\sqrt{R^2-r_2^2}=\sqrt{R^2-8}\).
\(\therefore O_1 O_2=O O_1-O O_2=\sqrt{R^2-5}-\sqrt{R^2-8}=1\),
移项得 \(\sqrt{R^2-5}=1+\sqrt{R^2-8}\),两边平方并化简得 \(\sqrt{R^2-8}=1\).
\(\therefore R^2=9\),\(R=3\),
\(\therefore\)球的表面积 \(S_{\text {球 }}=4 \pi \times 3^2=36 \pi\),球的体积 \(V_{\text {球 }}=\dfrac{4}{3} \pi \times 3^3=36 \pi\) .
【C组---拓展题】
1.在半径为\(15\)的球内有一个底面边长为\(12\sqrt{3}\)的内接正三棱锥,则此正三棱锥的体积为\(\underline{\quad \quad}\) .
参考答案
- 答案 \(864\sqrt{3}\)或\(216\sqrt{3}\)
解析 如图设球的球心为\(O\),内接正三棱锥为\(E-BCD\),
则三角形\(BCD\)为正三角形,边长\(BC=12\sqrt{3}\),外接圆半径 \(A C=\dfrac{\sqrt{3}}{3} \times 12 \sqrt{3}=12\),
球的半径\(OC=OE=15\),
(1)若\(E\)、\(A\)分别在球心\(O\)的两侧(如图1),
则在\(Rt△OAC\)中, \(O A=\sqrt{O C^2-A C^2}=\sqrt{15^2-12^2}=9\),
\(\therefore\)正三棱锥为\(E-BCD\)的高\(EA=OE+OA=15+9=24\),
\(\therefore\)正三棱锥为\(E-BCD\)的体积 \(V_{E-B C D}=\dfrac{1}{3} \times S_{\triangle B C D} \times E A\)
\(=\dfrac{1}{3} \times \dfrac{\sqrt{3}}{4} \times(12 \sqrt{3})^2 \times 24=\dfrac{1}{3} \times 108 \sqrt{3} \times 24=864 \sqrt{3}\),
(2)若\(E\)、\(A\)分别在球心\(O\)的同侧(如图2),则
在\(Rt△OAC\)中, \(O A=\sqrt{O C^2-A C^2}=\sqrt{15^2-12^2}=9\),
\(\therefore\)正三棱锥为\(E-BCD\)的高\(EA=OE-OA=15-9=6\),
\(\therefore\)正三棱锥为\(E-BCD\)的体积
\(V_{E-B C D}=\dfrac{1}{3} \times S_{\triangle B C D} \times E A=\dfrac{1}{3} \times \dfrac{\sqrt{3}}{4} \times(12 \sqrt{3})^2 \times 6\)\(=\dfrac{1}{3} \times 108 \sqrt{3} \times 6=216 \sqrt{3}\),
故答案为\(864\sqrt{3}\)或\(216\sqrt{3}\).
