P6818 [PA2013]Działka

前言

我太菜了。。。。

对着 jiangly 大佬的题解研究了一下午研究了一下午才搞出来（泪目。

作为一个蒟蒻，我就详细的讲一下我对与本题的理解。

题意

本题的的题意描述的还是比较明了。

在二维坐标系中，输入 \(n\) 个点 \(m\) 次询问，

每次询问，给出一个矩阵，

求出矩阵内极大凸包的面积。

题解

1.如何求面积

二维平面的计算几何题，较常见的做法就是利用叉积。本题亦如此。

叉积有个优美的性质，我们可以发现对于 \(\vec{a} \times \vec{b}\) 可以在二维平面赋予特殊意义（ \(S\) 为三角形面积）。

\(\vec{a} \times \vec{b} = 2S\)

利用这个性质我们就可以求出任意凸包的面积。

举个例子，\(4\) 个点坐标为 \((1 , 1) (1 , 3) (3 , 3) (3 , 1)\) 在此记为 \(0\) 号点到 \(3\) 号点，\(G\) 记为原点，

那要求出其凸包的面积就可以写作：

\({ \vec{G0} \times \vec{G3} + \vec{G3} \times \vec{G2} + \vec{G1} \times \vec{G0} + \vec{G1} \times \vec{G0} \over 2}\)

其实就可以理解为绿色的三角形相加。

再容斥一下减去红色三角(由于叉乘的顺寻原因出来的红色三角形负数)。

剩下的就是索要求的凸包面积。

因为本题 \(n \le 3000\) 我们可以考虑直接 \(O(n ^ 2)\) 预处理出每两个向量的叉乘(其实不是任意两个的叉乘，详见第三部分)。

呢么下面的任务就是快速找到凸包外面的点。

2.如何找凸包

如何找凸包呢？有一个十分优雅的方法。可以考虑寻找类似于四分之一扇形的凸包，然后每次旋转找到 \(4\) 个半圆再求和。假设我们先找右上角的扇形。

对于如下图形如何优美的找到凸包呢？

我们可以考虑将点以优先 \(x\) 从大到小后 \(y\) 从大到小的顺序找（过程可以顺便预处理前面提到的任意两点的距离）。

手模一下发现，我们先会从 \(1\) 号点就可以轻易的找到 \({1 , 3 , 4}\) 的点集。

呢如何记录高效的记录答案呢？

3.如何记录答案

直接枚举每个问题，显然会 T 飞。

考虑在记录两点间距离的时候直接记录最外面凸包的距离，例如前面的图片，在记录 \(\vec{1} \times \vec{4}\) 的时可以直接记录为 \(\vec{1} \times \vec{3} + \vec{3} \times \vec{4}\)。样我们在统计答案的时候实际上只需要记录只需要记录他最接近边界的两个点就可了。

考虑每一次记录答考虑使用线段树加扫描线的思想，如下图为每个点。

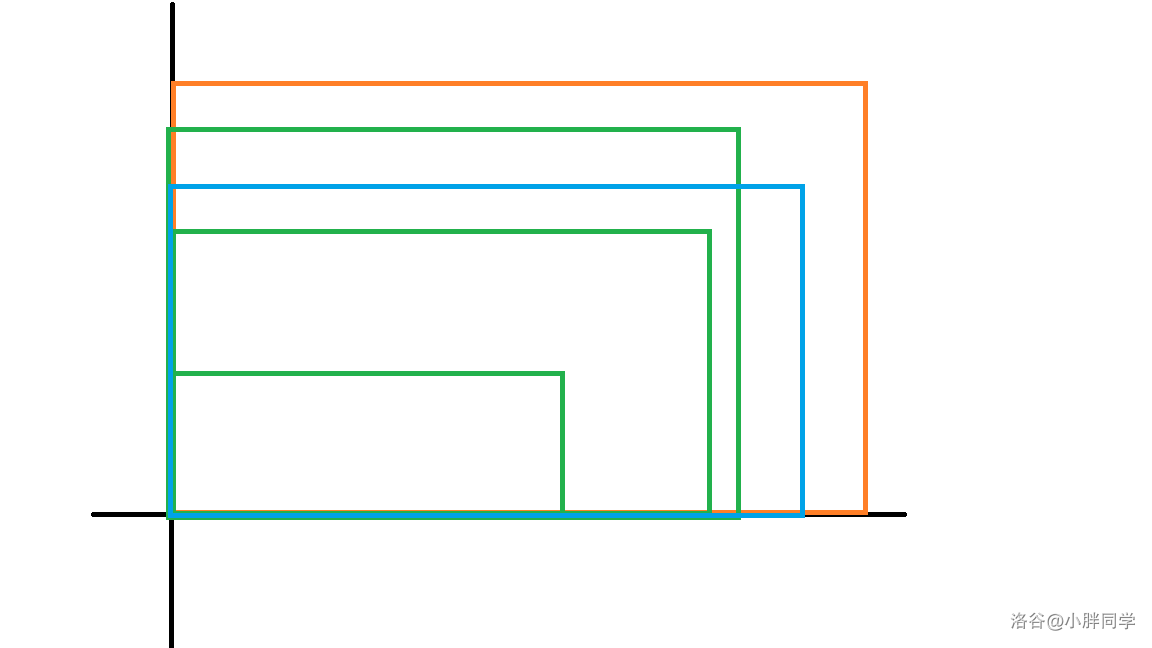
当我们更新完最外面的橙色的点还没有处理蓝色的点的时候，考虑有哪些区间里的提问是可以被更新的。

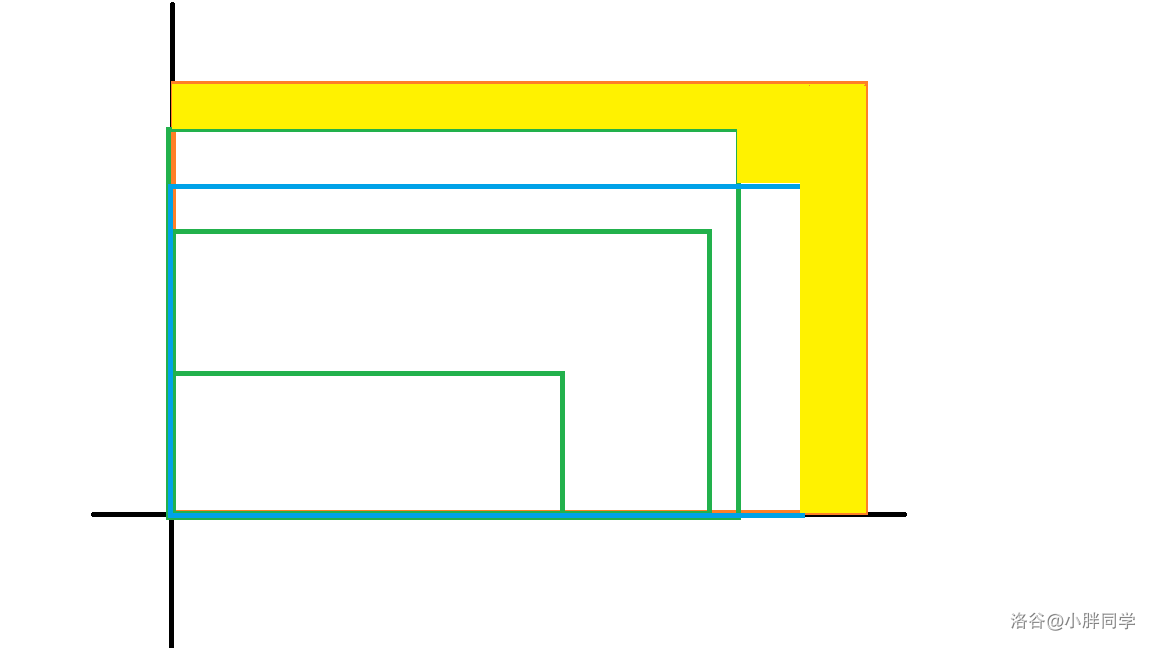
黄色的区间是可以被更新的，利用扫描线的思想做到 \(O(m \log m)\) 维护每个图形的边界。

\(\bullet\) 加强版

模拟赛出了这道题的加强版，若坐标的范围改成 \(-10^7 \le x ,y \le 10^7\)。

两个办法，一是使用效率更高的 zkw 线段树，二是数据离散化。

当然本题用普通线段树就可以切了。

Code

代码跟 jiangly 大佬的没有本质区别，就不粘了（doge去翻上一篇题解吧。