因为我也是看了大佬的题解才写的(第一问),自认为自己讲得不可能比他们再好了,但是因为好多第二问的题解都被hack了,所以这里详细讲一下第二问的正确做法。
初中平几课堂开课啦
其实思路很简单,利用贪心的思想,能往上走就往上走,能走多高就走多高,来看这个图:
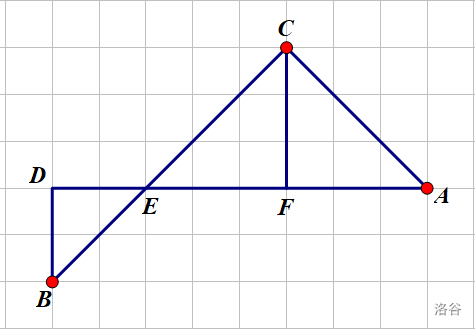
点 \(A\) 是当前点,点 \(B\) 是前一个点,点 \(C\) 是这个路径能到达的最高点,设 \(A\) 坐标是 \((x_1,y_1)\) , \(B\) 坐标为 \((x_0,y_0)\) 。
容易得出:
\[\because AD=x_1-x_0,BD=y_1-y_0=DE \]\[\therefore AE=(x_1-x_0)-(y_1-y_0)=x_1-x_0+y_0-y_1 \]\[\therefore CF=\frac{1}{2}AE=\frac{x_1-x_0+y_0-y_1}{2} \]\[\therefore y_C=y_1+CF=\frac{x_1-x_0+y_0+y_1}{2} \]第二问答案就是所有 \(C\) 的最大值,即:
maxn=max(maxn,(x1-x0+y0+y1)>>1);
但是,需要注意的是,如果在 \(B\) 点不能往上走,上面的公式就不好用了,比如这个hack:
18 3
2 2
4 2
12 6
ans:
1 6
画出来唯一解法是这样的:
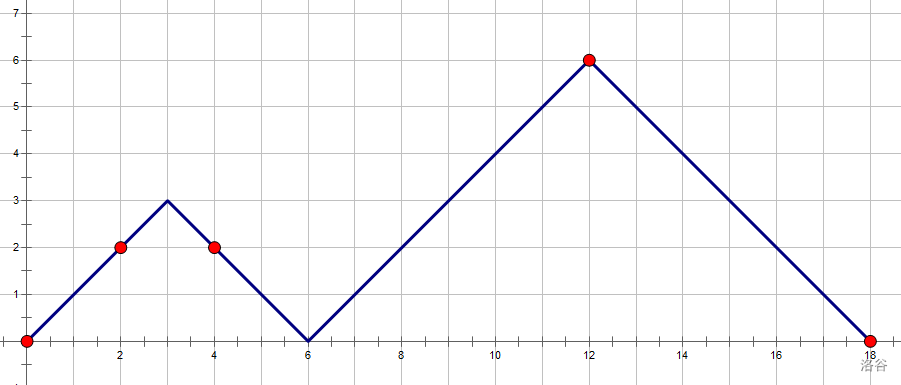
但如果我们按上面的方法做,第二问的答案会是8,为什么呢?
如果我们仍按以上方法算,第二问会被认为这样的:
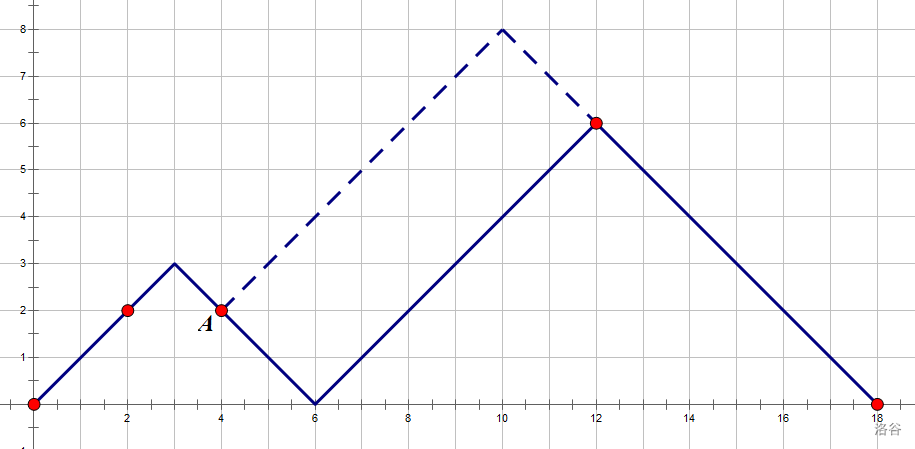
但显然这是错的,因为不满足题目所要求的函数极小值为 \(0\) 。
分析产生这种情况的原因:在计算第二问的时候,没有考虑到前一个点不能往上走的情况。
那么何时不能往上走呢?
也很简单,因为我们之前设 \(f_{i,0/1}\) 为第 \(i\) 个点上升/下降的方案数,则第 \(i\) 个点不能上升就是 \(f_{i,0}=0\) 的情况。
那么如果它不能上升,我们就让它下降到 \(0\) ,以这个点作为我们之前分析的 \(B\) 点,即:
if(!f[i-1][1])x0=x0+y0,y0=0;
这样第二问就结束了。第二问本身不难,但问题出在没有把情况像第一问一样考虑全,导致一些想当然的错误做法,因此告诫自己:
一定要在考虑问题时思考全面,实在不行把所有可能性罗列出来!
标签:frac,Luogu,第二,往上走,therefore,y0,P3336,x0 From: https://www.cnblogs.com/untitled0/p/luogu-p3396.html