初中数学老师在平面几何的第一节课就和我们说过:
点动成线,线动成面,面动成体。
即,由 \(i-1\) 维元素变化到 \(i\) 维的过程,就可以认为是将 \(i-1\) 维物体沿第 \(i\) 个方向平移的过程。
因此我们考虑一个二维的正方形平移得到三维的正方体的过程:
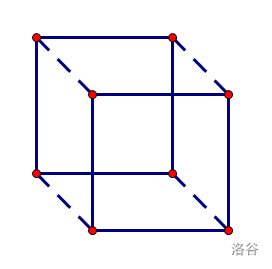
如果我们以平面的个数作为研究对象,不难看出,正方体中存在的平面有如下两个来源:
- 原来图形中的平面在经过平移后数量翻倍
- 原来的图形中的每一条线段在经过平移后都生成一个新的平面
推广到普遍结论:
- \(i-1\) 维元素中的 \(j\) 维元素在经过平移后数量翻倍
- \(i-1\) 维元素中的 \(j-1\) 维元素在经过平移后都生成一个新的 \(j\) 维元素
因此,如果我们设 \(f_{i,j}\) 为一个 \(i\) 维物体中 \(j\) 维元素的数量,并把不存在的元素,如 \(f_{i,-1}\) 和 \(f_{i,i+1}\) 等都看作 \(0\) ,我们可以得出如下递推式:
\[f_{0,0}=1 \]\[f_{i,j}=2f_{i-1,j}+f_{i-1,j-1} \]优化一下空间,我们可以写出如下的代码:
f[0][1]=1;//为了防止负下标溢出,将j统一加一
for(int i=1;i<=a;i++)
for(int j=i+1;i>0;j--)
f[j]=(2*f[j]+f[j-1])%Mod;
cout<<f[b+1]<<endl;
但是由于时间复杂度太过爆炸TLE了五个点……
接下来可以考虑根据生成函数优化:
设 \(F_i(x)\) 为第 \(i\) 行的生成函数,根据上述递推式,有:
\[F_0(x)=1 \]\[F_i(x)=(x+2)F_{i-1}(x) \]可以得出:
\[F_i(x)=(x+2)^i \]则有:
\[f_{i,j}=[j](x+2)^i \]根据二项式定理:
\[(a+b)^n=\sum_{i=0}^n \binom{n}{i}a^ib^{n-i} \]则有:
\[f_{i,j}=\binom{i}{j}2^{i-j} \]因此只需要 \(O(n)\) 分别求出阶乘和阶乘的逆元即可。
代码:
#include<bits/stdc++.h>
using namespace std;
typedef unsigned long long ll;
ll fac[100005]={1},inv[100005];
constexpr ll Mod=1e9+7;
ll qpow(ll a,ll b){//快速幂
ll ans=1;
while(b){
if(b&1)ans=ans*a%Mod;
a=a*a%Mod;
b>>=1;
}
return ans;
}
int main(){
int a,b;cin>>a>>b;
if(a<b)return cout<<0,0;
for(int i=1;i<=a;i++)fac[i]=fac[i-1]*i%Mod;
inv[a]=qpow(fac[a],Mod-2);//费马小定理
for(int i=a-1;i>=0;i--)inv[i]=inv[i+1]*(i+1)%Mod;
cout<<qpow(2,a-b)*fac[a]%Mod*inv[b]%Mod*inv[a-b]%Mod;
return 0;
}