标签：plt temp 手册 数组 np NumPy 我们

原文：Learning NumPy Array

协议：CC BY-NC-SA 4.0

译者：飞龙

一、NumPy 入门

让我们开始吧。 我们将在不同的操作系统上安装 NumPy 和相关软件，并查看一些使用 NumPy 的简单代码。 正如“序言”所述，SciPy 与 NumPy 密切相关，因此您会在本章中看到 SciPy 这个名字。 在本章的最后，您将找到有关如何在线获取更多信息的指南，如果您陷入困境或不确定解决问题的最佳方法。

在本章中，我们将学习以下技能：

• 在 Windows，Linux 和 Macintosh 上安装 Python，SciPy，Matplotlib，IPython 和 NumPy
• 编写简单的 NumPy 代码
• 相加数组
• 利用在线资源和帮助

Python

NumPy 基于 Python，因此需要安装 Python。 在某些操作系统上，已经安装了 Python 。 但是，您需要检查 Python 版本是否与要安装的 NumPy 版本兼容。 Python 有许多实现，包括商业实现和发行版。 在本书中，我们将重点介绍标准的 CPython 实现，该实现可保证与 NumPy 兼容。

NumPy 具有适用于 Windows，各种 Linux 发行版和 Mac OS X 的二进制安装程序。如果您愿意，还可以提供源代码发行版。 您需要在系统上安装 Python 2.4.x 或更高版本。 Python 2.7.6 是目前拥有的最好的 Python 版本，因为大多数科学的 Python 库都支持它。

在 Windows 上安装 NumPy，Matplotlib，SciPy 和 IPython

在 Windows 上安装 NumPy 是必需的，但幸运的是，我们将详细介绍简单的任务。 您只需要下载安装程序，向导就会指导您完成安装步骤。 建议安装 Matplotlib，SciPy 和 IPython。 但是，这不是享受本书所必需的。 我们将采取的行动如下：

• 选择适当的版本。 在此示例中，我们选择了numpy-1.8.0-win32-superpack-python2.7.exe。

• 双击打开 EXE 安装程序。

  

  • 现在，我们可以看到 NumPy 及其功能的描述，如上一个屏幕截图所示。 单击下一步按钮。* 如果您安装了 Python，则应自动检测到它。 如果未检测到，则可能是您的路径设置错误。 本章最后列出了资源，以防您在安装 NumPy 时遇到问题。

  

  • 在此示例中，找到了 Python 2.7。 如果找到 Python，请单击下一步按钮，否则，单击取消按钮并安装 Python（如果没有，则无法安装 NumPy）。 单击下一步按钮上的。 这是无可挽回的意义。 很好，但是最好确保要安装到正确的目录，依此类推。 现在开始真正的安装。 可能还要等一下。
  • 在以下位置安装带有 Enthought 发行版的 SciPy 和 Matplotlib。

  注意

  安装人员周围的情况正在迅速发展。 在成熟的各个阶段都存在其他替代方法。 可能需要将msvcp71.dll文件放在您的C:\Windows\system32目录中。 您可以在这个页面上获得它。 IPython 网站上提供了 Windows IPython 安装程序。

在 Linux 上安装 NumPy，Matplotlib，SciPy 和 IPython

在 Linux 上安装 NumPy 和相关的推荐软件取决于您所拥有的发行版。 我们将讨论如何从命令行安装 NumPy，尽管您可能会使用图形化安装程序。 这取决于您的发行版（发行版）。 安装 Matplotlib，SciPy，和 IPython 的命令是相同的-仅包名称不同。 建议安装 Matplotlib，SciPy 和 IPython，但这是可选的。

大多数 Linux 发行版都有 NumPy 包。 我们将为一些受欢迎的 Linux 发行版进行必要的步骤：

• 从命令行运行以下指示信息以在 Red Hat 上安装 NumPy：

  yum install python-numpy
  
  

• 要在 Mandriva 上安装 NumPy，请运行以下命令行指令：

  urpmi python-numpy
  
  

• 要在 Gentoo 上安装 NumPy，请运行以下命令行指令：

  sudo emerge numpy
  
  

• 要在 Debian 或 Ubuntu 上安装 NumPy，我们需要输入以下内容：

  sudo apt-get install python-numpy
  
  

下表概述了 Linux 发行版以及 NumPy，SciPy，Matplotlib 和 IPython 的相应包名称：

Linux 发行版	NumPy	SciPy	Matplotlib	IPython
Arch Linux	python-numpy	python-scipy	python-matplotlib	ipython
Debian	python-numpy	python-scipy	python-matplotlib	ipython
Fedora	numpy	python-scipy	python-matplotlib	ipython
Gentoo	dev-python/numpy	scipy	matplotlib	ipython
OpenSUSE	python-numpy, python-numpy-devel	python-scipy	python-matplotlib	ipython
Slackware	numpy	scipy	matplotlib	ipython

在 Mac OS X 上安装 NumPy，Matplotlib 和 SciPy

您可以根据需要，在 Mac 上使用图形安装程序来安装 NumPy， Matplotlib 和 SciPy，也可以在命令行中使用端口管理器（例如 MacPorts 或 Fink）来安装 NumPy， Matplotlib 和 SciPy。

注意

我们可以从 SourceForge 网站上获取 NumPy 安装程序。 Matplotlib 和 SciPy 也存在类似的文件。 只需将前一个 URL 中的numpy更改为scipy或matplotlib即可。 在撰写本文时，IPython 还没有 GUI 安装程序。 下载适当的 DMG 文件，如以下屏幕截图所示； 通常最新的是最好的。 另一种选择是 SciPy Superpack。 无论选择哪个选项，确保不影响 Apple 提供的 Python 库都不会影响到系统 Python 库的更新不会对已经安装的软件产生负面影响，这一点很重要。

我们将通过以下步骤使用 GUI 安装程序安装 NumPy ：

• 双击，即打开的框的图标，即下标以.mpkg结尾的下标。 我们将看到安装程序的欢迎屏幕。

• 单击继续按钮转到自述文件屏幕，在该屏幕上，我们将简要介绍 NumPy，如以下屏幕截图所示：

  

  • 单击继续按钮转到许可证屏幕。
  • 阅读许可证，在提示您接受许可证时，单击继续按钮，然后单击接受按钮。 继续浏览下一个屏幕，最后单击完成按钮。

另外，我们可以通过 MacPorts 路由或使用 Fink 安装 NumPy，SciPy，Matplotlib，和 IPython。 以下安装步骤将安装所有这些包。 本书中的教程仅需要 NumPy，因此请省略您不感兴趣的包。

• 要使用 MacPorts 进行安装，请键入以下命令：

  sudo port install py-numpy py-scipy py-matplotlib py-ipython
  
  

• Fink 还具有用于 NumPy 的包：scipy-core-py24，scipy-core-py25和scipy-core-py26。 SciPy 包为：scipy-py24，scipy-py25和scipy-py26。 我们可以使用以下命令安装 NumPy 和本书将在 Python 2.6 中使用的其他推荐包：

  fink install scipy-core-py26 scipy-py26 matplotlib-py26
  
  

从源代码构建

作为最后的方法，或者如果我们想获得最新的代码，则可以从源代码构建。 在实践中，这并不难，但是根据您的操作系统，您可能会遇到问题。 随着操作系统和相关软件的迅速发展，您最好的办法就是在线搜索或寻求帮助。 在本章中，我们为寻求帮助的好地方提供了指导。

从源代码安装 NumPy 的步骤很简单，并在此处给出。 我们可以使用.git检索 NumPy 的源代码，如下所示：

git clone git://github.com/numpy/numpy.git numpy

使用以下命令在/usr/local上安装：

python setup.py build
sudo python setup.py install --prefix=/usr/local

要构建，我们需要一个 C 编译器，例如 GCC 和python-dev或python-devel包中的 Python 头文件。

NumPy 数组

在完成 NumPy 的安装之后，该看看 NumPy 数组了。 在进行数值运算时，NumPy 数组比 Python 列表更有效。 NumPy 数组实际上是经过广泛优化的专用对象。 与等效的 Python 代码相比，NumPy 代码需要更少的显式循环。 这是基于向量化的。

如果我们回到高中数学，那么我们应该记住标量和向量的概念。 例如，数字 2 是标量。 当我们加 2 和 2 时，我们正在执行标量加法。 我们可以从一组标量中形成一个向量。 用 Python 编程术语，我们将得到一维数组。 这个概念当然可以扩展到更高的维度。 对两个数组执行加法之类的运算可以简化为一组标量运算。 在直接的 Python 中，我们将通过遍历第一个数组中的每个元素并将其添加到第二个数组中的相应元素的循环来实现。 但是，这比数学中的方法更为冗长。 在数学中，我们将两个向量的加法视为单个运算。 NumPy 数组也是这样做的方式，并且使用低级 C 例程进行了某些优化，这使这些基本操作更加有效。 在下一章中，我们将更详细地介绍 NumPy 数组。

相加数组

想象一下我们要添加两个向量a和b。 这里在数学上使用向量，即一维数组。 我们将在第 4 章，“在 NumPy 中进行简单的预测分析”，了解代表矩阵的专用 NumPy 数组。 例如，向量a保持整数0至n的平方。 如果n等于3，则a包含0，1或4。 向量b包含整数0至n的立方，因此，如果n等于3，则向量b等于0，1或8。 您将如何使用普通 Python 做到这一点？ 在提出解决方案之后，我们将其与等效的 NumPy 进行比较。

以下函数使用不带 NumPy 的纯 Python 解决了向量加法问题：

def pythonsum(n):
   a = range(n)
   b = range(n)
   c = []

   for i in range(len(a)):
       a[i] = i ** 2
       b[i] = i ** 3
       c.append(a[i] + b[i])

   return c

以下是使用 NumPy 实现的函数：

def numpysum(n):
  a = numpy.arange(n) ** 2
  b = numpy.arange(n) ** 3
  c = a + b
  return c

请注意，numpysum()不需要for循环。 另外，我们使用了 NumPy 的arange函数，该函数为我们创建了一个整数0至n的 NumPy 数组。 arange函数已导入； 这就是为什么它以numpy为前缀的原因。

有趣的来了。 请记住，在“序言”中提到，关于数组操作，NumPy 更快。 但是，Numpy 快了多少？ 以下程序将通过测量numpysum和pythonsum函数的经过时间（以微秒为单位）向我们展示。 它还打印向量和的最后两个元素。 让我们检查一下在使用 Python 和 NumPy 时我们得到的答案是否相同：

##!/usr/bin/env/python

import sys
from datetime import datetime
import numpy as np

"""
 This program demonstrates vector addition the Python way.
 Run from the command line as follows

  python vectorsum.py n

 where n is an integer that specifies the size of the vectors.

 The first vector to be added contains the squares of 0 up to n.
 The second vector contains the cubes of 0 up to n.
 The program prints the last 2 elements of the sum and the elapsed time.
"""

def numpysum(n):
   a = np.arange(n) ** 2
   b = np.arange(n) ** 3
   c = a + b

   return c

def pythonsum(n):
   a = range(n)
   b = range(n)
   c = []

   for i in range(len(a)):
       a[i] = i ** 2
       b[i] = i ** 3
       c.append(a[i] + b[i])

   return c

size = int(sys.argv[1])

start = datetime.now()
c = pythonsum(size)
delta = datetime.now() - start
print "The last 2 elements of the sum", c[-2:]
print "PythonSum elapsed time in microseconds", delta.microseconds

start = datetime.now()
c = numpysum(size)
delta = datetime.now() - start
print "The last 2 elements of the sum", c[-2:]
print "NumPySum elapsed time in microseconds", delta.microseconds

1000，2000和3000向量元素的程序输出如下：

$ python vectorsum.py 1000
The last 2 elements of the sum [995007996, 998001000]
PythonSum elapsed time in microseconds 707
The last 2 elements of the sum [995007996 998001000]
NumPySum elapsed time in microseconds 171
$ python vectorsum.py 2000
The last 2 elements of the sum [7980015996, 7992002000]
PythonSum elapsed time in microseconds 1420
The last 2 elements of the sum [7980015996 7992002000]
NumPySum elapsed time in microseconds 168
$ python vectorsum.py 4000
The last 2 elements of the sum [63920031996, 63968004000]
PythonSum elapsed time in microseconds 2829
The last 2 elements of the sum [63920031996 63968004000]
NumPySum elapsed time in microseconds 274

显然，NumPy 比等效的普通 Python 代码快得多。 可以肯定的是，无论是否使用 NumPy，我们都会得到相同的结果。 但是，打印结果在表示形式上有所不同。 请注意，numpysum函数的结果没有任何逗号。 怎么会？ 显然，我们不是在处理 Python 列表，而是在处理 NumPy 数组。 在“序言”中提到，NumPy 数组是用于数值数据的专用数据结构。 我们将在第 2 章， “NumPy 基础知识”中了解有关 NumPy 数组的更多信息。

在线资源和帮助

NumPy 和 SciPy 的主要文档网站位于这里。 在此网页上，我们可以在这个页面和用户指南以及一些教程中浏览 NumPy 参考。

NumPy 在这个页面上有一个包含大量文档的 Wiki。

NumPy 和 SciPy 论坛可以在这个页面上找到。

流行的 Stack Overflow 软件开发论坛上有数百个标记为numpy的问题。 要查看它们，请转到这里。

如果您确实遇到问题，或者想随时了解 NumPy 的发展，可以订阅 NumPy 讨论邮件列表。 电子邮件地址为<[email protected]>。 每天的电子邮件数量不是很高，而且几乎没有垃圾邮件可言。 最重要的是，积极参与 NumPy 的开发人员还会回答讨论组提出的问题。 完整列表可以在这个页面中找到。

对于 IRC 用户，在 IRC 上有一个 IRC 通道。 通道名为，称为#scipy，但是您也可以问 NumPy 问题，因为 SciPy 基于 NumPy，因此 SciPy 用户也了解 NumPy。 任何时候，SciPy 频道上至少有 50 名成员。

总结

在本章中，我们安装了 NumPy 和其他推荐软件，这些软件将在某些教程中使用。 我们启动了向量加法程序，并确信 NumPy 具有出色的性能。 此外，我们还探索了可用的 NumPy 文档和在线资源。

在下一章中，我们将深入研究并探索一些基本概念，包括数组和数据类型。

二、NumPy 基础

安装 NumPy 并使一些代码正常工作之后，该介绍 NumPy 的基础知识了。 本章向您介绍 NumPy 和数组的基础。 在本章的最后，您将对 NumPy 数组及其关联函数有基本的了解。

我们将在本章中介绍的主题如下：

• 数据类型
• 数组类型
• 类型转换
• 创建数组
• 索引
• 花式索引
• 切片
• 修改形状

NumPy 数组对象

NumPy 具有一个称为 ndarray的多维数组对象。 它由两部分组成，如下所示：

• 实际数据
• 一些描述数据的元数据

大多数数组操作均保持原始数据不变。 更改的唯一方面是元数据。

在上一章中，我们已经学习了如何使用arange()函数创建数组。 实际上，我们创建了一个包含一组数字的一维数组。 ndarray对象可以具有多个维度。

NumPy 数组的优点

NumPy 数组是通用的同类数组-数组中的项必须为相同类型（存在异类的特殊数组类型）。 好处是，如果我们知道数组中的项目属于同一类型，则很容易确定数组所需的存储大小。 NumPy 数组可以对整个数组执行向量化操作。 将此与 Python 列表进行对比，通常情况下，您必须遍历该列表并一次对每个元素执行操作。 而且，NumPy 使用优化的 C API 进行这些操作，使其特别快。

NumPy 数组的索引就像在 Python 中一样，从 0 开始。数据类型由特殊对象表示。 这些对象将在本章中进一步详细讨论。

我们将再次使用arange()函数创建一个数组（请参见本书代码包Chapter02文件夹中的arrayattributes.py文件）。 在本章中，您将看到已经导入 NumPy 的 IPython 会话中的代码片段。 以下代码段向我们展示了如何获取数组的数据类型：

In: a = arange(5)
In: a.dtype
Out: dtype('int64')

数组a的数据类型为int64（至少在我的机器上），但是如果使用 32 位 Python，则可能会得到int32作为输出。 在这两种情况下，我们都处理整数（64 位或 32 位）。 除了数组的数据类型外，了解其形状也很重要。 第 1 章， “NumPy 入门”中的示例演示了如何创建向量（实际上是一维 NumPy 数组）。 向量通常用于数学中，但是大多数时候我们需要高维的对象。 让我们确定在本节前面创建的向量的形状：

In: a
Out: array([0, 1, 2, 3, 4])
In: a.shape
Out: (5,)

如您所见，向量具有五个元素，其值范围从0到4。 数组的shape属性是一个元组； 在这种情况下，是一个元素的元组，其中包含每个维度的长度。

创建多维数组

既然我们知道如何创建向量，就可以创建多维 NumPy 数组了。 创建矩阵之后，我们将再次想要显示其形状（请参见本书代码包Chapter02文件夹中的arrayattributes.py文件），如以下代码段所示：

• 要创建多维数组，请参见以下代码：

  In: m = array([arange(2), arange(2)])
  In: m
  Out:
  array([[0, 1],[0, 1]])
  

• 要显示数组形状，请参见以下代码行：

  In: m.shape
  Out: (2, 2)
  

我们使用arange()函数创建了一个2 x 2的数组。 没有任何警告，array()函数出现在舞台上。

array()函数从提供给它的对象创建一个数组。 该对象必须是类似数组的，例如 Python 列表。 在前面的示例中，我们传入了一个数组列表。 该对象是array()函数的唯一必需参数。 NumPy 函数倾向于具有许多带有预定义默认值的可选参数。

选择数组元素

从时间到时间，我们将要选择数组的特定元素。 我们将看一下如何执行此操作，但首先，让我们再次创建一个2 x 2矩阵（请参见本书代码包Chapter02文件夹中的elementselection.py文件）：

In: a = array([[1,2],[3,4]])
In: a
Out:
array([[1, 2],       [3, 4]])

这次是通过将列表列表传递给array()函数来创建矩阵的。 现在，我们将一次选择矩阵的每个项目，如以下代码片段所示。 请记住，索引从 0 开始编号。

In: a[0,0]
Out: 1
In: a[0,1]
Out: 2
In: a[1,0]
Out: 3
In: a[1,1]
Out: 4

如您所见，选择数组的元素非常简单。 对于数组a，我们只使用符号a[m,n]，其中m和n是数组中该项的索引。

NumPy 数值类型

Python 具有整数类型，浮点类型和复杂类型。 但是，这对于科学计算而言还不够。 实际上，我们需要更多具有不同精度的数据类型，因此，该类型的内存大小也有所不同。 因此，NumPy 具有更多的数据类型。 NumPy 数值类型的大多数以数字结尾。 该数字指示与类型关联的位数。 下表（根据 NumPy 用户指南改编）概述了 NumPy 数值类型：

类型	描述
bool	布尔（True或False）存储为一个位
inti	平台整数（通常为int32或int64）
int8	整数，范围为 -128 至 127
int16	整数，范围为 -32768 至 32767
int32	整数，范围为-2 ** 31至2 ** 31 -1
int64	整数，范围为-2 ** 63至2 ** 63 -1
uint8	无符号整数，范围为 0 到 255
uint16	无符号整数，范围为 0 到 65535
uint32	无符号整数，范围为 0 到2 ** 32-1
uint64	无符号整数，范围为 0 到2 ** 64-1
float16	半精度浮点数，具有符号位，5 位指数和 10 位尾数
float32	单精度浮点数，具有符号位，8 位指数和 23 位尾数
float64或float	双精度浮点数，具有符号位，11 位指数和 52 位尾数
complex64	复数，由两个 32 位浮点数（实部和虚部）表示
complex128或complex	复数，由两个 64 位浮点数（实部和虚部）表示

对于每种数据类型，都有一个对应的转换函数（请参见本书代码包的Chapter02文件夹中的numericaltypes.py文件），如以下代码片段所示：

In: float64(42)
Out: 42.0
In: int8(42.0)
Out: 42
In: bool(42)
Out: True
In: bool(0)
Out: False
In: bool(42.0)
Out: True
In: float(True)
Out: 1.0
      In: float(False)
     Out: 0.0

许多函数都有一个数据类型参数，该参数通常是可选的：

In: arange(7, dtype=uint16)
Out: array([0, 1, 2, 3, 4, 5, 6], dtype=uint16)

重要的是要知道您不允许将复数转换为整数类型的数字。 尝试执行此操作会触发TypeError，如以下屏幕截图所示：

将复数转换为浮点类型数也是如此。 顺便提及， j部分是复数的虚数系数。 但是，您可以将浮点数转换为复数，例如complex(1.0)。 复数的实部和虚部可以分别通过real()和imag()函数提取。

数据类型对象

数据类型对象是numpy.dtype类的实例。 数组再次具有数据类型。 确切地说，NumPy 数组中的每个元素都具有相同的数据类型。 数据类型对象可以告诉您数据的大小（以字节为单位）。 字节的大小由dtype类的itemsize属性给出（请参见本书代码包的Chapter02文件夹中的dtypeattributes.py文件），如以下代码行所示：

In: a.dtype.itemsize
Out: 8

字符代码

NumPy 包含字符代码，以便与 Numeric 向后兼容。 Numeric 是 NumPy 的前身。 不建议使用它们，但是此处提供了代码，因为它们会在多个位置弹出。 您应该改用dtype对象。 下表显示了不同的数据类型和与其关联的字符代码：

类型	字符码
整数	i
无符号整数	u
单精度浮点	f
双精度浮点	d
布尔	b
复数	D
字符串	S
Unicode	U
无	V

查看下面的代码以创建一个单精度浮点数数组（请参见本书代码包的Chapter02文件夹中的charcodes.py文件）：

In: arange(7, dtype='f')
Out: array([ 0.,  1.,  2.,  3.,  4.,  5.,  6.], dtype=float32)
Likewise this creates an array of complex numbers
In: arange(7, dtype='D')
Out: array([ 0.+0.j,  1.+0.j,  2.+0.j,  3.+0.j,  4.+0.j,  5.+0.j,  6.+0.j])

dtype构造器

我们有多种创建数据类型的方式。 以浮点数据为例（请参见本书代码包的Chapter02文件夹中的dtypeconstructors.py文件），如下所示：

• 我们可以使用通用的 Python 浮点数，如以下代码行所示：

  In: dtype(float)
  Out: dtype('float64')
  

• 我们可以使用字符代码指定一个单精度浮点数，如以下代码行所示：

  In: dtype('f')
  Out: dtype('float32')
  

• 我们可以使用双精度浮点字符代码，如以下代码行所示：

  In: dtype('d')
  Out: dtype('float64')
  

• 我们可以给数据类型构造器一个两个字符的代码。 第一个字符表示类型，第二个字符是一个数字，用于指定数据类型中的字节数（数字 2、4 和 8 分别对应于 16 位，32 位和 64 位浮点数），在以下代码行中显示：

  In: dtype('f8')
  Out: dtype('float64')
  

可以通过调用sctypeDict.keys()找到所有数据类型名称的列表：

In: sctypeDict.keys()
Out: [0, …'i2','int0']

dtype属性

dtype类具有许多有用的属性。 例如，我们可以通过dtype的属性获取有关数据类型的字符代码的信息（请参见本书代码包Chapter02文件夹中的dtypeattributes2.py文件），如以下代码片段所示：

In: t = dtype('Float64')
In: t.char
Out: 'd'

type属性对应于数组元素的对象类型：

In: t.type
Out: <type 'numpy.float64'>

dtype的str属性给出了数据类型的字符串表示形式。 它从代表字节序的字符开始（如果适用），然后是字符代码，后跟与每个数组项所需的字节数相对应的数字。 这里的字节顺序表示字节在 32 位或 64 位字中的排序方式。 按照大端顺序，最高有效字节先存储，由“ >”指示。 按照小端顺序，最低有效字节首先存储，由<指示，如以下代码行所示：

In: t.str
Out: '<f8'

创建记录数据类型

记录数据类型是一种异构数据类型-认为它表示电子表格或数据库中的一行。 以记录数据类型为例，我们将为商店库存创建一条记录。 该记录包含以 40 个字符的字符串表示的商品名称，商店中以 32 位整数表示的商品数量，最后以 32 位浮点数表示的商品价格。 以下步骤显示了如何创建记录数据类型（请参见本书代码包的Chapter02文件夹中的record.py文件）：

1. 要创建记录，请检查以下代码片段：

   In: t = dtype([('name', str_, 40), ('numitems', int32), ('price', float32)])
   In: t
   Out: dtype([('name', '|S40'), ('numitems', '<i4'), ('price', '<f4')])
   

2. 要查看字段的类型，请检查以下代码段：

   In: t['name']
   Out: dtype('|S40')
   

如果不为array()函数提供数据类型，则将假定它正在处理浮点数。 现在要创建一个数组，我们实际上必须指定数据类型，如以下代码行所示； 否则，我们将获得TypeError：

In: itemz = array([('Meaning of life DVD', 42, 3.14), ('Butter', 13, 2.72)], dtype=t)
In: itemz[1]
Out: ('Butter', 13, 2.7200000286102295)

我们创建了一个记录数据类型，它是一个异构数据类型。 记录包含一个名称（作为字符串），一个数字（一个整数）和一个以浮点值表示的价格。

一维切片和索引

一维 NumPy 数组的切片与 Python 列表的切片一样。 我们可以从3到7的索引中选择一个数组的，以提取3到6的元素（请参见本书代码包Chapter02文件夹中的slicing1d.py文件） ），如以下代码段所示：

In: a = arange(9)
In: a[3:7]
Out: array([3, 4, 5, 6])

我们可以以两个为步长从索引0到7中选择元素，如以下代码行所示：

In: a[:7:2]
Out: array([0, 2, 4, 6])

就像在 Python 中一样，我们可以使用负索引并反转数组，如以下代码行所示：

In: a[::-1]
Out: array([8, 7, 6, 5, 4, 3, 2, 1, 0])

修改数组形状

另一个重复执行的任务是将数组展平。 在这种情况下，展平意味着将多维数组转换为一维数组。 在此示例中，我们将展示许多方法从展平开始操作数组形状：

• ravel()：我们可以使用ravel()函数完成的拼合（请参见本书代码包Chapter02文件夹中的shapemanipulation.py文件），如以下代码所示：

  In: b
  Out:
  array([[[ 0,  1,  2,  3],[ 4,  5,  6,  7],[ 8,  9, 10, 11]],[[12, 13, 14, 15],[16, 17, 18, 19],[20, 21, 22, 23]]])
  In: b.ravel()
  Out:
  array([ 0,  1,  2,  3,  4,  5,  6,  7,  8,  9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23])
  

• flatten()：适当命名的函数flatten()与ravel()相同，但是flatten()总是分配新的内存，而ravel()可能返回数组的视图。 这意味着我们可以按以下方式直接操作数组：

  In: b.flatten()
  Out:
  array([ 0,  1,  2,  3,  4,  5,  6,  7,  8,  9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23])
  

• shape：除了reshape()函数，我们还可以直接使用元组来设置形状，如下所示：

  In: b.shape = (6,4)
  In: b
  Out:
  array([[ 0,  1,  2,  3],[ 4,  5,  6,  7],[ 8,  9, 10, 11],[12, 13, 14, 15],[16, 17, 18, 19],[20, 21, 22, 23]])
  

  如您所见，这将直接更改数组。 现在我们有一个6 x 4的数组。

• transpose()：在线性代数中，通常转置矩阵。 我们也可以使用transpose()函数来做到这一点，如以下代码所示：

  In: b.transpose()
  Out:
  array([[ 0,  4,  8, 12, 16, 20],[ 1,  5,  9, 13, 17, 21],[ 2,  6, 10, 14, 18, 22],[ 3,  7, 11, 15, 19, 23]])
  

• resize()：resize()方法的工作方式与reshape()方法相同，但是修改了它操作的数组：

  In: b.resize((2,12))
  In: b
  Out:
  array([[ 0,  1,  2,  3,  4,  5,  6,  7,  8,  9, 10, 11],[12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23]])
  

堆叠数组

数组可以水平，深度或垂直堆叠。 为此，我们可以使用vstack()，dstack()，hstack()，column_stack()，row_stack()和concatenate()函数。 首先，让我们设置一些数组（请参见本书代码包的Chapter02文件夹中的stacking.py文件），如以下代码所示：

In: a = arange(9).reshape(3,3)
In: a
Out:
array([[0, 1, 2],[3, 4, 5],[6, 7, 8]])
In: b = 2 * a
In: b
Out:
array([[ 0,  2,  4],[ 6,  8, 10],[12, 14, 16]])

以下是不同类型的堆叠：

• 水平堆叠：从水平堆叠开始，我们将形成一个ndarray元组并将其提供给hstack()函数。 显示如下：

  In: hstack((a, b))
  Out:
  array([[ 0,  1,  2,  0,  2,  4],[ 3,  4,  5,  6,  8, 10],[ 6,  7,  8, 12, 14, 16]])
  

  我们可以使用concatenate()函数实现相同的功能，如下所示：

  In: concatenate((a, b), axis=1)
  Out:
  array([[ 0,  1,  2,  0,  2,  4],[ 3,  4,  5,  6,  8, 10],[ 6,  7,  8, 12, 14, 16]])
  

  下图显示了水平堆叠：

  

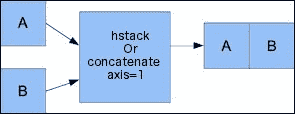
• 垂直堆叠：通过垂直堆叠，再次形成元组。 这次，它被提供给vstack()函数。 可以看到如下：

  In: vstack((a, b))
  Out:
  array([[ 0,  1,  2],[ 3,  4,  5],[ 6,  7,  8],[ 0,  2,  4],[ 6,  8, 10],[12, 14, 16]])
  

  concatenate()函数在将轴参数设置为0的情况下产生相同的结果。 这是axis参数的默认值，如以下代码所示：

  In: concatenate((a, b), axis=0)
  Out:
  array([[ 0,  1,  2],[ 3,  4,  5],[ 6,  7,  8],[ 0,  2,  4],[ 6,  8, 10],[12, 14, 16]])
  

  请参阅下图进行垂直堆叠：

  

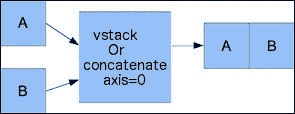
• 深度堆叠：当然还有使用dstack()和元组的深度堆叠。 这意味着沿第三轴（深度）堆叠数组列表。 例如，我们可以彼此堆叠图像数据的二维数组：

  In: dstack((a, b))
  Out:
  array([[[ 0,  0],[ 1,  2],[ 2,  4]],[[ 3,  6],[ 4,  8],[ 5, 10]],[[ 6, 12],[ 7, 14],[ 8, 16]]])
  

• 列堆叠：column_stack()函数按列堆叠一维数组。 显示如下：

  In: oned = arange(2)
  In: oned
  Out: array([0, 1])
  In: twice_oned = 2 * oned
  In: twice_oned
  Out: array([0, 2])
  In: column_stack((oned, twice_oned))
  Out:
  array([[0, 0],[1, 2]])
  

  二维数组以hstack()的方式堆叠，如以下代码所示：

  In: column_stack((a, b))
  Out:
  array([[ 0,  1,  2,  0,  2,  4],[ 3,  4,  5,  6,  8, 10],[ 6,  7,  8, 12, 14, 16]])
  In: column_stack((a, b)) == hstack((a, b))
  Out:
  array([[ True,  True,  True,  True,  True,  True],[ True,  True,  True,  True,  True,  True],[ True,  True,  True,  True,  True,  True]], dtype=bool)
  

  是的，您猜对了！ 我们用==运算符比较了两个数组。 这不漂亮吗？

• 行堆叠：NumPy 当然也具有执行行堆叠的函数。 它被称为row_stack()，对于一维数组，它只是将数组按行堆叠为二维数组：

  In: row_stack((oned, twice_oned))
  Out:
  array([[0, 1],[0, 2]])
  

  二维数组的row_stack()函数结果等于vstack()函数结果，如下所示：

  In: row_stack((a, b))
  Out:
  array([[ 0,  1,  2],[ 3,  4,  5],[ 6,  7,  8],[ 0,  2,  4],[ 6,  8, 10],[12, 14, 16]])
  In: row_stack((a,b)) == vstack((a, b))
  Out:
  array([[ True,  True,  True],[ True,  True,  True],[ True,  True,  True],[ True,  True,  True],[ True,  True,  True],[ True,  True,  True]], dtype=bool)
  

拆分数组

可以在垂直，水平或深度方向拆分数组。 涉及的函数是hsplit()，vsplit()，dsplit()和split()。 我们既可以将数组拆分为相同形状的数组，也可以指示拆分之后应该发生的位置。

• 水平分割：随后的代码将一个数组沿其水平轴分割为三个大小和形状相同的片段（请参见本书代码包Chapter02文件夹中的splitting.py文件）：

  In: a
  Out:
  array([[0, 1, 2],[3, 4, 5],[6, 7, 8]])
  In: hsplit(a, 3)
  Out:
  [array([[0],[3],[6]]),array([[1],[4],[7]]),array([[2],[5],[8]])]
  

  将其与 split()函数的调用以及附加参数axis=1进行比较：

  In: split(a, 3, axis=1)
  Out:
  [array([[0],[3],[6]]),array([[1],[4],[7]]),array([[2],[5],[8]])]
  

• 垂直分割：vsplit()函数沿垂直轴分割数组：

  In: vsplit(a, 3)
  Out: [array([[0, 1, 2]]), array([[3, 4, 5]]), array([[6, 7, 8]])]
  

  split()函数与axis=0一起也沿垂直轴拆分了一个数组：

  In: split(a, 3, axis=0)
  Out: [array([[0, 1, 2]]), array([[3, 4, 5]]), array([[6, 7, 8]])]
  

• 深度分割： dsplit()函数毫不奇怪，深度拆分数组。 我们将需要一个排名第三的数组：

  In: c = arange(27).reshape(3, 3, 3)
  In: c
  Out:
  array([[[ 0,  1,  2],[ 3,  4,  5],[ 6,  7,  8]],[[ 9, 10, 11],[12, 13, 14],[15, 16, 17]],[[18, 19, 20],[21, 22, 23],[24, 25, 26]]])
  In: dsplit(c, 3)
  Out:
  [array([[[ 0],[ 3],[ 6]],[[ 9],[12],[15]],[[18],[21],[24]]]),array([[[ 1],[ 4],[ 7]],[[10],[13],[16]],[[19],[22],[25]]]),array([[[ 2],[ 5],[ 8]],[[11],[14],[17]],[[20],[23],[26]]])]
  

数组属性

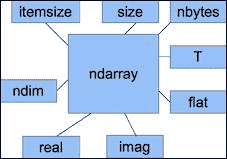
除了，shape和dtype属性外，ndarray还有许多其他属性，如下表所示：

• ndim：此属性为提供数组维数（请参见本书代码包包Chapter02文件夹中的arrayattributes2.py文件）：

  In: b
  Out:
  array([[ 0,  1,  2,  3,  4,  5,  6,  7,  8,  9, 10, 11],[12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23]])
  In: b.ndim
  Out: 2
  

• size：此属性显示元素数。 如下所示：

  In: b.size
  Out: 24
  

• itemsize：此属性给出数组中每个元素的字节数：

  In: b.itemsize
  Out: 8
  

• nbytes：此属性为提供数组所需的字节总数。 它只是itemsize和size属性的乘积：

  In: b.nbytes
  Out: 192
  In: b.size * b.itemsize
  Out: 192
  

• T：该属性与transpose()函数具有相同的作用，如下所示：

  In: b.resize(6,4)
  In: b
  Out:
  array([[ 0,  1,  2,  3],[ 4,  5,  6,  7],[ 8,  9, 10, 11],[12, 13, 14, 15],[16, 17, 18, 19],[20, 21, 22, 23]])
  In: b.T
  Out:
  array([[ 0,  4,  8, 12, 16, 20],[ 1,  5,  9, 13, 17, 21],[ 2,  6, 10, 14, 18, 22],[ 3,  7, 11, 15, 19, 23]])
  

  如果数组的排名低于 2，我们将只获得数组的视图：

  In: b.ndim
  Out: 1
  In: b.T
  Out: array([0, 1, 2, 3, 4])
  

  NumPy 中的复数由j表示。 例如，我们可以创建一个包含复数的数组：

  In: b = array([1.j + 1, 2.j + 3])
  In: b
  Out: array([ 1.+1.j,  3.+2.j])
  

• real：此属性为我们提供了数组的实部；如果数组本身仅包含实数，则为数组本身：

  In: b.real
  Out: array([ 1.,  3.])
  

• imag：此属性包含数组的虚部：

  In: b.imag
  Out: array([ 1.,  2.])
  

  如果数组包含复数，则数据类型也将自动变为复数：

  In: b.dtype
  Out: dtype('complex128')
  In: b.dtype.str
  Out: '<c16'
  

• flat: 这个属性返回一个numpy.flatiter对象。 这是获取flatiter的唯一方法 -- 我们无权访问flatiter构造器。 展开迭代器使我们能够像遍历展开数组一样遍历数组，如以下代码所示：

  In: b = arange(4).reshape(2,2)
  In: b
  Out:
  array([[0, 1],[2, 3]])
  In: f = b.flat
  In: f
  Out: <numpy.flatiter object at 0x103013e00>
  In: for item in f: print item
     .....:
  0
  1
  2
  3
  

  可以使用flatiter对象直接获取元素，如下所示：

  In: b.flat[2]
  Out: 2
  

  也可以按如下方式获取多个元素：

  In: b.flat[[1,3]]
  Out: array([1, 3])
  

  flat属性是可设置的。 设置flat属性的值会导致覆盖整个数组的值，如下所示：

  In: b.flat = 7
  In: b
  Out:
  array([[7, 7],[7, 7]])
  

  您甚至可以按以下方式获取选定的元素：

  In: b.flat[[1,3]] = 1
  In: b
  Out:
  array([[7, 1],[7, 1]])
  

下图显示了ndarray的不同属性：

转换数组

我们可以通过tolist()函数将 NumPy 数组转换为 Python 列表（请参见本书代码包Chapter02文件夹中的arrayconversion.py文件），如下所示：

• 要将数组转换为列表，请检查以下代码片段：

  In: b
  Out: array([ 1.+1.j,  3.+2.j])
  In: b.tolist()
  Out: [(1+1j), (3+2j)]
  

• astype()函数将数组转换为指定类型的数组，如以下代码所示：

  In: b
  Out: array([ 1.+1.j,  3.+2.j])
  In: b.astype(int)
  /usr/local/bin/ipython:1: ComplexWarning: Casting complex values to real discards the imaginary part
    #!/usr/bin/python
  Out: array([1, 3])
  

注意

从复杂类型转换为int时，我们将丢失虚部。

astype()函数还接受类型名称作为字符串，如以下代码片段所示：

In: b.astype('complex')
Out: array([ 1.+1.j,  3.+2.j])

这次不会显示任何警告，因为我们使用了正确的数据类型。

创建视图和副本

在关于ravel()函数的示例中，提到了视图。 视图不应与数据库视图的概念混淆。 NumPy 世界中的视图不是只读的，并且您无法保护基础数据。 了解何时使用共享数组视图以及何时拥有数组数据副本非常重要。 例如，切片将创建一个视图。 这意味着，如果您将切片分配给变量，然后更改基础数组，则此变量的值将更改。 我们将根据著名的 Lena 图像创建一个数组，复制该数组，创建一个视图，最后修改视图。 Lena 图像数组来自 SciPy 函数。

1. 要创建 Lena 数组的副本，请使用以下代码行：

   acopy = lena.copy()
   

2. 现在，要创建数组的视图，请使用以下代码行：

   aview = lena.view()
   

3. 使用平面迭代器将视图的所有值设置为0，如下所示：

   aview.flat = 0
   

最终结果是只有一张图像显示了花花公子模型。 其他人被完全审查，如下图所示。

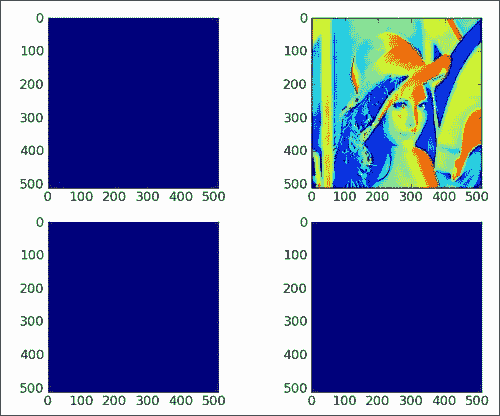
请参阅本部分的以下代码（不带注释以节省空间；有关完整的代码，请参见本书代码包Chapter02文件夹中的copy_view.py文件），该信息显示了数组视图的行为。 并复制：

import scipy.misc
import matplotlib.pyplot as plt

lena = scipy.misc.lena()
acopy = lena.copy()
aview = lena.view()
plt.subplot(221)
plt.imshow(lena)
plt.subplot(222)
plt.imshow(acopy)
plt.subplot(223)
plt.imshow(aview)
aview.flat = 0
plt.subplot(224)
plt.imshow(aview)
plt.show()

如您所见，通过在程序末尾更改视图，我们更改了原始的 Lena 数组。 此产生了三个蓝色（如果您正在观看黑白图像，则为黑色）图像。 复制的数组不受影响。 重要的是要记住，视图不是只读的。

花式索引

花式索引是不包含整数或切片的索引，这是常规索引。 在本节中，我们将应用花式索引将 Lena 图像的对角线值设置为0。 这将沿着对角线绘制黑线，穿过它，这不是因为图像有问题，而是作为一种练习。 执行以下步骤进行花式索引编制：

1. 将第一个对角线的值设置为0。 要将对角线值设置为0，我们需要为x和y值定义两个不同的范围，如下所示：

   lena[range(xmax), range(ymax)] = 0
   

2. 现在，将另一个对角线的值设置为0。 要设置另一个对角线的值，我们需要使用一组不同的范围，但是原理保持不变，如下所示：

   lena[range(xmax-1,-1,-1), range(ymax)] = 0
   

最后，我们得到以下对角线被划掉的图像：

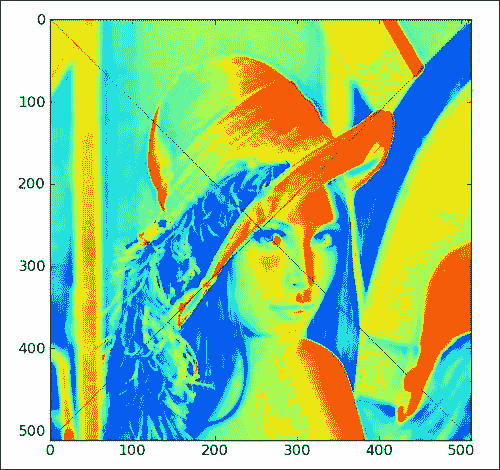
此部分的以下代码不带注释。 本书的代码包Chapter02文件夹中的fancy.py文件中包含完整代码。

import scipy.misc
import matplotlib.pyplot as plt

lena = scipy.misc.lena()
xmax = lena.shape[0]
ymax = lena.shape[1]
lena[range(xmax), range(ymax)] = 0
lena[range(xmax-1,-1,-1), range(ymax)] = 0
plt.imshow(lena)
plt.show()

我们为x和y值定义了单独的范围。 这些范围用于索引 Lena 数组。 花式索引是基于内部 NumPy 迭代器对象执行的。 这可以通过执行以下三个步骤来实现：

1. 创建迭代器对象。
2. 将迭代器对象绑定到数组。
3. 通过迭代器访问数组元素。

位置列表索引

让我们使用ix_()函数来随机播放 Lena 图像。 此函数从多个序列创建一个网格。 作为参数，我们给出一维序列，并且该函数返回 NumPy 数组的元组。 例如，检查以下代码片段：

In : ix_([0,1], [2,3])
Out:
(array([[0], [1]]), array([[2, 3]]))

要使用位置列表为数组建立索引，请执行以下步骤：

1. 随机排列数组索引。 使用numpy.random模块的shuffle()函数创建一个随机索引数组，如以下代码行所示。 该函数顺便更改了数组inplace。

   def shuffle_indices(size):
      arr = np.arange(size)
      np.random.shuffle(arr)
   
      return arr
   

2. 现在，按如下所示绘制改组后的索引：

   plt.imshow(lena[np.ix_(xindices, yindices)])
   

我们得到的是一个完全混乱的 Lena，如下图所示：

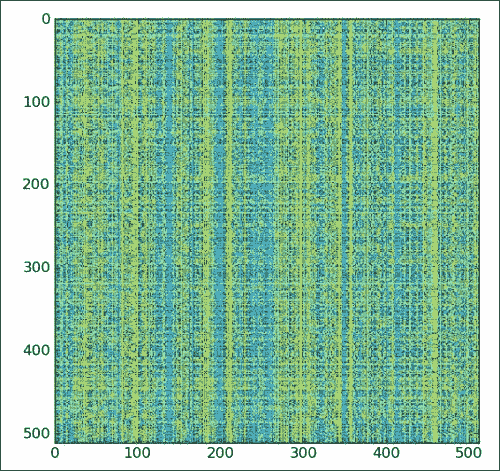
此部分的以下代码不带注释。 完整的代码可以在本书代码包包的Chapter02文件夹中的ix.py文件中找到。

import scipy.misc
import matplotlib.pyplot
import numpy as np

lena = scipy.misc.lena()
xmax = lena.shape[0]
ymax = lena.shape[1]

def shuffle_indices(size):
   arr = np.arange(size)
   np.random.shuffle(arr)

   return arr

xindices = shuffle_indices(xmax)
np.testing.assert_equal(len(xindices), xmax)
yindices = shuffle_indices(ymax)
np.testing.assert_equal(len(yindices), ymax)
plt.imshow(lena[np.ix_(xindices, yindices)])
plt.show()

使用布尔值索引数组

布尔索引是基于布尔数组的索引，属于奇特索引的类别。 由于布尔索引是幻想索引的一种形式，因此它的工作方式基本相同。 表示在特殊的迭代器对象的帮助下进行索引。 执行以下步骤为数组建立索引：

1. 首先，我们创建一个在对角线上带有点的图像。 这在某种程度上类似于“花式索引”部分。 这次，我们在图像的对角线上选择取四点为模，如以下代码片段所示：

   def get_indices(size):
      arr = np.arange(size)
      return arr % 4 == 0
   

2. 然后，我们只需应用此选择并绘制点，如以下代码片段所示：

   lena1 = lena.copy() 
   xindices = get_indices(lena.shape[0])
   yindices = get_indices(lena.shape[1])
   lena1[xindices, yindices] = 0
   plt.subplot(211)
   plt.imshow(lena1)
   

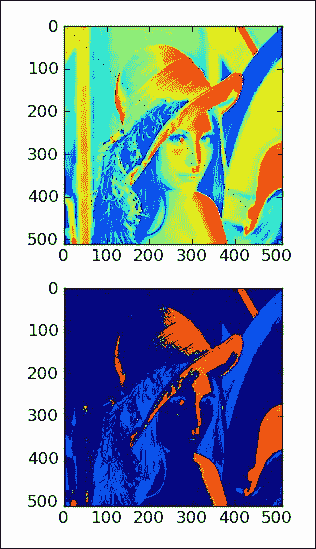
3. 在最大值的四分之一到四分之三之间选择数组值，并将它们设置为0，如下面的代码行所示：

   lena2[(lena > lena.max()/4) & (lena < 3 * lena.max()/4)] = 0
   

带有两个新图像的图如下所示：

以下是该部分的代码（请参见本书代码包Chapter02文件夹中的boolean_indexing.py文件）：

import scipy.misc
import matplotlib.pyplot as plt
import numpy as np

lena = scipy.misc.lena()

def get_indices(size):
   arr = np.arange(size)
   return arr % 4 == 0

lena1 = lena.copy() 
xindices = get_indices(lena.shape[0])
yindices = get_indices(lena.shape[1])
lena1[xindices, yindices] = 0
plt.subplot(211)
plt.imshow(lena1)
lena2 = lena.copy() 
lena2[(lena > lena.max()/4) & (lena < 3 * lena.max()/4)] = 0
plt.subplot(212)
plt.imshow(lena2)
plt.show()

数独步幅技巧

我们甚至可以使用 NumPy 做更华丽的事情。 ndarray类具有一个字段strides，该字段是一个元组，指示通过数组时每个维度要步进的字节数。 数独是起源于日本的流行拼图。 尽管在其他国家/地区以前也以类似的形式知道它。 如果您不了解数独，那可能会更好，因为它极易上瘾。 让我们对将数独谜题拆分为3 x 3正方形的问题应用一些大的技巧：

1. 首先定义数独拼图数组，如以下代码片段所示。 这是一个实际已解决的数独难题的内容（为简洁起见，省略了部分数组）。

   sudoku = np.array([[2, 8, 7, 1, 6, 5, 9, 4, 3],[9, 5, 4, 7, 3, 2, 1, 6, 8],…[7, 3, 6, 2, 8, 4, 5, 1, 9]])
   

2. 现在计算步幅。 ndarray的itemsize字段为我们提供了数组中的字节数。 itemsize计算步幅如下：

   strides = sudoku.itemsize * np.array([27, 3, 9, 1])
   

3. 现在，我们可以使用np.lib.stride_tricks模块的as_strided()函数将拼图分解为正方形，如以下代码行所示：

   squares = np.lib.stride_tricks.as_strided(sudoku, shape=shape, strides=strides)
   print(squares)
   

这将打印单独的数独方块（为了节省空间，一些方块被省略了），如下所示：

[[[[2 8 7][9 5 4][6 1 3]]…[[[8 7 9][4 2 1][3 6 5]]…[[[1 9 8][5 4 2][7 3 6]]…[[4 2 6][3 8 7][5 1 9]]]]

以下是此示例的完整源代码（请参见本书代码包Chapter02文件夹中的strides.py文件）：

import numpy as np

sudoku = np.array([[2, 8, 7, 1, 6, 5, 9, 4, 3],[9, 5, 4, 7, 3, 2, 1, 6, 8],[6, 1, 3, 8, 4, 9, 7, 5, 2],[8, 7, 9, 6, 5, 1, 2, 3, 4],[4, 2, 1, 3, 9, 8, 6, 7, 5],[3, 6, 5, 4, 2, 7, 8, 9, 1],[1, 9, 8, 5, 7, 3, 4, 2, 6],[5, 4, 2, 9, 1, 6, 3, 8, 7],[7, 3, 6, 2, 8, 4, 5, 1, 9]])

shape = (3, 3, 3, 3)
strides = sudoku.itemsize * np.array([27, 3, 9, 1])
squares = np.lib.stride_tricks.as_strided(sudoku, shape=shape, strides=strides)
print(squares)

我们应用了步幅技巧，将数独谜题分解为3 x 3的正方形。 步幅告诉我们通过数独数组时，每个步骤需要跳过多少字节。

广播数组

简而言之，即使操作数的形状不同，NumPy 也会尝试执行操作。 在本节中，我们将一个数组和一个标量相乘。 标量扩展为数组操作数的形状，然后执行乘法。 我们将下载音频文件并制作一个更安静的新版本：

1. 首先，读取 WAV 文件。 我们将使用标准的 Python 代码下载 Austin Powers 的音频文件，叫做“Smashing，baby”。 SciPy 具有wavfile模块，可让您加载声音数据或生成 WAV 文件。 如果已安装 SciPy，则我们应该已经有此模块。 read()函数返回数据数组和采样率。 在这个例子中，我们只关心数据。

   sample_rate, data = scipy.io.wavfile.read(WAV_FILE)
   

2. 使用 Matplotlib 绘制原始 WAV 数据。 为子图命名为Original，如以下代码行所示：

   plt.subplot(2, 1, 1)
   plt.title("Original")
   plt.plot(data)
   

3. 现在创建一个新数组。 我们将使用 NumPy 制作更安静的音频样本。 只是通过乘以常量来创建具有较小值的新数组。 这就是广播魔术发生的地方。 最后，由于 WAV 格式，我们需要确保与原始数组具有相同的数据类型。

   newdata = data * 0.2
   newdata = newdata.astype(np.uint8)
   

4. 现在，可以将这个新数组写入新的 WAV 文件，如下所示：

   scipy.io.wavfile.write("quiet.wav",
       sample_rate, newdata)
   

5. 使用 Matplotlib 绘制新数据数组，如下所示：

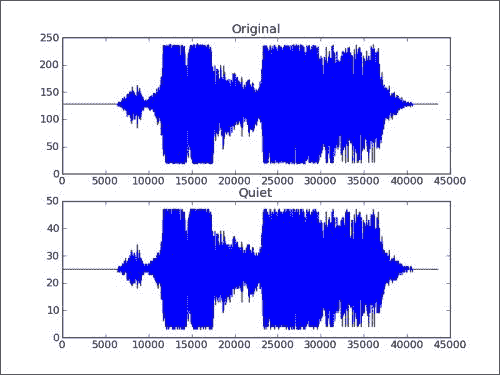
   matplotlib.pyplot.subplot(2, 1, 2)
   matplotlib.pyplot.title("Quiet")
   matplotlib.pyplot.plot(newdata)
   matplotlib.pyplot.show()
   

结果是原始 WAV 文件数据和具有较小值的新数组的图，如下图所示：

以下是本节的完整代码（请参见本书代码包Chapter02文件夹中的broadcast.py文件）：

import scipy.io.wavfile
import matplotlib.pyplot
import urllib2
import numpy as np

response = urllib2.urlopen('http://www.thesoundarchive.com/austinpowers/smashingbaby.wav')
print response.info()
WAV_FILE = 'smashingbaby.wav'
filehandle = open(WAV_FILE, 'w')
filehandle.write(response.read())
filehandle.close()
sample_rate, data = scipy.io.wavfile.read(WAV_FILE)
print "Data type", data.dtype, "Shape", data.shape
plt.subplot(2, 1, 1)
plt.title("Original")
plt.plot(data)
newdata = data * 0.2
newdata = newdata.astype(np.uint8)
print "Data type", newdata.dtype, "Shape", newdata.shape
scipy.io.wavfile.write("quiet.wav",
    sample_rate, newdata)
plt.subplot(2, 1, 2)
plt.title("Quiet")
plt.plot(newdata)
plt.show()

总结

在本章中，我们从 NumPy 基础知识中学到了很多东西：数据类型和数组。 数组有几个描述它们的属性。 我们了解到，这些属性之一是数据类型，在 NumPy 中，该数据类型由完整的对象表示。

就像 Python 列表一样，可以有效地对 NumPy 数组进行切片和索引。 NumPy 数组具有处理多个维度的附加功能。

数组的形状可以通过多种方式进行操作，例如堆叠，调整大小，重新塑形和拆分。 本章演示了许多用于形状处理的便捷函数。

了解了基础知识之后，是时候继续使用第 3 章，“使用 NumPy 进行基本数据分析”的常用函数进行数据分析了。 这包括基本统计和数学函数的使用。

三、使用 NumPy 的基本数据分析

在本章中，我们将通过历史天气数据示例学习基本数据分析。 我们将学习函数，这些函数使使用 NumPy 更加容易。

在本章中，我们将涵盖以下主题：

• 数组上的函数
• 从包含天气数据的文件中加载数组
• 简单的数学和统计函数

数据集简介

首先，我们将了解 NumPy 的文件 I/O。 数据通常存储在文件中。 如果您无法读取和写入文件，您将走不远。

荷兰皇家气象学院（KNMI）在线提供每日天气数据。 KNMI 是荷兰气象局，总部位于德比尔特（De Bilt）。 让我们从 De Bilt 气象站下载其中一个 KNMI 文件。 该文件大约为 10 MB。 它有一些文本，用荷兰语和英语解释了这些数据。 在此之下是逗号分隔值格式的数据。 我将元数据和实际数据分离到单独的文件中。 不需要分隔，因为从 NumPy 加载时可以跳过行。 我用 NumPy 编写了一个简单的脚本，以确定在分离过程中创建的 CSV 文件中数据集的最高和最低温度。

温度以十分之一摄氏度为单位给出。 三列包含温度：

• 24 小时的平均温度
• 每日最低温度
• 每日最高温度

现在我们将忽略平均温度。 另请注意，缺少值，因此我们将它们转换为非数字（NaN）值。 NaN 是 Python 中浮点数的特殊值。 最后，我们可以提出以下简单脚本（请参见本书代码包包的Chapter03文件夹中的intro.py文件）：

import numpy as np
import sys

to_float = lambda x: float(x.strip() or np.nan)

## Measurements are in tenths of degrees
min_temp, max_temp = np.loadtxt(sys.argv[1], delimiter=',',usecols=(12, 14), unpack=True, converters={12: to_float, 14: to_float}) * .1
print "# Records", len(min_temp), len(max_temp)
print "Minimum", np.nanmin(min_temp)
print "Maximum", np.nanmax(max_temp)

此脚本打印记录数以及最低和最高温度：

## Records 40996 40996
Minimum -24.8
Maximum 36.8

注意

我们使用loadtxt函数读取文件。 默认情况下，loadtxt尝试将所有数据转换为浮点数。 为此，loadtxt函数具有特殊的参数。 该参数称为converters，它是将列与所谓的转换器函数链接在一起的字典。 我们还指定逗号作为要使用的字段和列的分隔符。 有关更多详细信息，请参考这里。 KNMI 引用温度值的十分之一摄氏度，因此需要一个简单的乘法。 nanmin和nanmax函数与 NumPy max和min函数相同，但它们也忽略了 NaN。

确定每日温度范围

在气象学中，每日温度范围或昼夜温度变化在地球上并不重要。 在地球上或通常在不同星球上的沙漠地区，变化更大。 我们将在上一个示例中下载的数据看一下在每日温度范围内的情况：

1. 要分析温度范围，我们将需要导入 NumPy 包和 NumPy 遮罩数组：

   import numpy as np
   import sys
   import numpy.ma as ma
   from datetime import datetime as dt
   

2. 我们将加载比上一部分中加载的数据更多的数据：YYYYMMDD格式的测量日期和每日平均温度。 日期需要特殊转换。 首先将日期字符串转换为日期，然后转换为数字，如下所示：

   to_float = lambda x: float(x.strip() or np.nan)
   to_date = lambda x: dt.strptime(x, "%Y%m%d").toordinal()
   
   dates, avg_temp, min_temp, max_temp = np.loadtxt(sys.argv[1], delimiter=',', usecols=(1, 11, 12, 14), unpack=True, converters={1: to_date, 12: to_float, 14: to_float})
   

3. 让我们计算最低和最高温度低于零摄氏度（凝固点）的天数百分比：

   print "% days min < 0", 100 * len(min_temp[min_temp < 0])/float(len(min_temp))
   print "% days max < 0", 100 * len(max_temp[max_temp < 0])/float(len(max_temp))
   

   每日最高温度低于零的可能性似乎为 3%。 每年大约 10 天。 最低每日温度更可能低于零，可能性为 18%。 大约一年两个月。 显然不是连续几个月。

   % days min below 0 18.1944579959 
   % days max below 0 2.81978729632
   
   

   不幸的是，我们仍然存在缺失值的问题。 解决此问题的一种方法是使用遮罩数组。 遮罩数组是 NumPy 数组的一种特殊类型，通常包含缺失，无效或可疑值。

4. 现在，要解决缺失值的问题，只需将一个由isnan函数创建的遮罩给带遮罩的数组一个即可。 我们将计算温度的平均值和标准差，以及每日温度范围的最小值和最大值：

   ranges = max_temp - min_temp
   print "Minimum daily range", np.nanmin(ranges)
   print "Maximum daily range", np.nanmax(ranges)
   
   masked_ranges = ma.array(ranges, mask = np.isnan(ranges))
   print "Average daily range", masked_ranges.mean()
   print "Standard deviation", masked_ranges.std()
   
   masked_mins = ma.array(min_temp, mask = np.isnan(min_temp))
   print "Average minimum temperature", masked_mins.mean(), "Standard deviation", masked_mins.std()
   
   masked_maxs = ma.array(max_temp, mask = np.isnan(max_temp))
   print "Average maximum temperature", masked_maxs.mean(), "Standard deviation", masked_maxs.std()
   

   显然，平均每日范围是 8 度，而平均最小值在 5 度左右，而最大值在 13 度左右。 在编写代码时打印了以下值； 自然，如果您使用更新的数据来运行程序，结果可能会有所不同：

   Minimum daily range 0.6 
   Maximum daily range 22.2 
   Average daily range 8.20358580315 
   Standard deviation 3.72983839106 
   Average minimum temperature 5.39096231248 
   Standard deviation 5.85061308004 
   Average maximum temperature 13.5945481156 
   Standard deviation 7.40767291657
   
   

您可以在本书代码包Chapter03文件夹中的daily_temperature_range.py文件中找到此示例的代码。

寻找全球变暖的证据

根据全球变暖理论，自 19 世纪末以来，地球上的温度平均在上升。 在上个世纪直到现在，据称温度已经升高了约 0.8 度。 显然，这种变暖的大部分发生在最近的两三个十年中。 将来，我们可以预期温度会进一步升高，从而导致干旱，热浪和其他不愉快的现象。 显然，某些地区将受到比其他地区更大的打击。 已经提出了几种解决方案，包括减少温室气体排放和通过在大气中扩散特殊气体以反射更多的阳光来进行地球工程。

我们从荷兰气象研究所（KNMI）下载的数据不足以证明全球变暖是否真实，但我们当然可以进一步进行研究。 例如，我们可以检查数据集上半部分 De Delt（收集数据的地方）中的温度是否低于下半部分。 我们可以做的另一件事是绘制年度平均温度。 据我所知，De Bilt 是荷兰中部的一个没有重工业的小镇。 稍后我们需要导入 NumPy 和 Matplotlib 来创建图。 执行以下步骤来计算年平均温度：

1. 我们将加载平均每日温度和相应的日期。 实际上，我们会立即将日期转换为年份，以便能够计算出年平均温度：

   to_year = lambda x: dt.strptime(x, "%Y%m%d").year
   
   years, avg_temp = np.loadtxt(sys.argv[1], delimiter=',', usecols=(1, 11), unpack=True, converters={1: to_year})
   
   # Measurements are in .1 degrees Celsius
   avg_temp = .1 * avg_temp
   
   N = len(avg_temp)
   print "First Year", years[0], "Last Year", years[-1]
   assert N == len(years)
   assert years[:N/2].mean() < years[N/2:].mean()
   

   如您所见，在代码段的末尾会进行一些检查，这会打印以下输出：

   First Year 1901.0 Last Year 2013.0
   
   

2. 将平均每日温度值分成两半后，我们可以计算和比较两半的算术平均值。 在这里，我们也使用 NumPy ndarray方法来比较标准差：

   print "First half average", avg_temp[:N/2].mean(), "Std Dev", avg_temp[:N/2].std()
   print "Second half average", avg_temp[N/2:].mean(), "Std Dev", avg_temp[N/2:].std()
   

   这为我们提供了以下输出：

   First half average 9.19078446678 Std Dev 6.42457006016 
   Second half average 9.78066152795 Std Dev 6.34152195332
   
   

   数据集的后半部分似乎平均温度略高。

3. 计算年平均温度很简单。 对于每一年，使用对应于该年的where函数查找数组索引。 利用这些指标，我们然后计算每年的平均值并将其存储：

   avgs = []
   year_range = range(int(years[0]), int(years[-1]) - 1)
   
   for year in year_range:
      indices = np.where(years == year)
      avgs.append(avg_temp[indices].mean())
   
   plt.plot(year_range, avgs, 'r-', label="Yearly Averages")
   plt.plot(year_range, np.ones(len(avgs)) * np.mean(avgs))
   plt.legend(prop={'size':'x-small'})
   plt.show()
   

   结果得到以下图。 为了进行比较，还通过图的中间绘制了所有平均温度的平均值。 请注意，自 1980 年以来，年平均气温似乎在上升（请参阅本书代码包Chapter03文件夹中的global_warming.py文件）。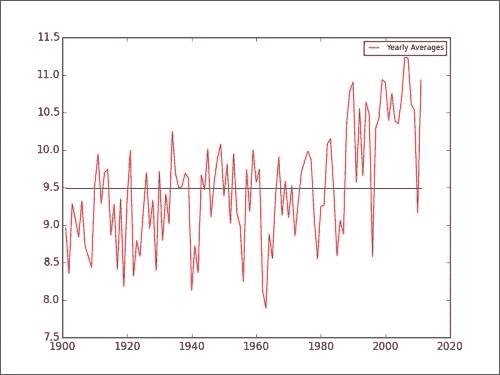

   

比较太阳辐射与温度

当涉及温度时，太阳当然是的一个非常重要的因素。 不幸的是，KNMI 的 De Bilt 数据集缺少许多有关太阳辐射的数据。 数据以焦耳每平方厘米为单位。 文件中还有其他变量，这些变量是从太阳辐射得出的，例如以小时为单位的日照时间。

我们将对辐射数据进行一些分析，绘制直方图，并将其与每日平均温度进行比较。 为了进行比较，我们将计算辐射与温度之间的相关系数，并绘制平均温度和辐射的年度相对变化图。 最初，有一个散点图似乎是一个好主意，但是对于成千上万的数据点来说看起来并不正确，因此，决定压缩数据。 后来，作者意识到从 1960 年左右开始存在辐射，因此绘制每年的相关系数可能会更好。 这留给读者练习。

我们需要导入 NumPy，NumPy 遮罩数组模块和 Matplotlib。 比较太阳辐射与温度的步骤如下：

1. 我们将加载日期并将其转换为年份，然后加载平均温度和辐射。 后者会遗漏很多值，因此我们将遗漏的值转换为 NaN，然后​​从辐射数据中创建一个遮罩数组：

   to_float = lambda x: float(x.strip() or np.nan)
   to_year = lambda x: dt.strptime(x, "%Y%m%d").year
   
   years, avg_temp, Q = np.loadtxt(sys.argv[1], delimiter=',', usecols=(1, 11, 20), unpack=True, converters={1: to_year, 20: to_float})
   ma
   # Measurements are in .1 degrees Celsius
   avg_temp = .1 * avg_temp
   
   Q = ma.masked_invalid(Q)
   

2. 我们将看看辐射的最小，最大，平均值和标准差。 另外，我们将使用corrcoef函数打印温度和辐射的相关系数。 要计算系数，我们需要通过避免 NaN 值来正确匹配数据。 同样，我们必须获得 NumPy 返回的相关矩阵的非对角线值之一。 遮罩数组的compressed方法将所有非遮罩数据作为一维数组返回：

   print "# temperature values", len(avg_temp), "# radiation values", len(Q.compressed())
   print "Radiation Min", Q.min(), "Radiation Max", Q.max()
   print "Radiation Average", Q.compressed().mean(), "Std Dev", Q.std()
   
   match_temp =  avg_temp[np.logical_not(np.isnan(Q))]
   print "Correlation Coefficient", np.corrcoef(match_temp, Q.compressed())[0][1]
   

   该脚本将输出以下输出：

   # temperature values 40996 # radiation values 20361 
   Radiation Min 7.0 Radiation Max 3081.0 
   Radiation Average 957.156082707 Std Dev 740.68047373 
   Correlation Coefficient 0.62767320286
   
   

   如您所见，相关性并不强。

3. 我们已经进行了年度平均。 现在，我们将辐射量平均化。 我们要做的另一项是用百分比来计算我们感兴趣的变量的相对变化。 diff函数默认为我们提供相邻数组值之间的一阶差：

   avg_temps = []
   avg_qs = []
   year_range = range(int(years[0]), int(years[-1]) - 1)
   
   for year in year_range:
      indices = np.where(years == year)
      avg_temps.append(avg_temp[indices].mean())
      avg_qs.append(Q[indices].mean())
   
   def percents(a):
      return 100 * np.diff(a)/a[:-1]
   

4. 我们将用 Matplotlib 绘制辐射直方图以及年平均温度和辐射的相对变化。 Matplotlib 是一个开放源代码的 Python 绘图库，许多人认为它是基本栈的一部分。 有关更多信息，请参阅《Python 开发人员的Matplotlib》，Packt Publishing。 该书的第二版由该书的作者共同撰写，应于 2014 年出版。

   plt.subplot(211)
   plt.title("Global Radiation Histogram")
   plt.hist(Q.compressed(), 200)
   
   plt.subplot(212)
   plt.title("Changes in Average Yearly Temperature & Radiation")
   plt.plot(year_range[1:], percents(avg_temps), label='% Change Temperature')
   plt.plot(year_range[1:], percents(avg_qs), label='% Change Radiation')
   plt.legend(prop={'size':'x-small'})
   plt.show()
   

   Matplotlib subplot函数从多个图创建表格或网格。 在此示例中，我们使用 211 表示将有两个图，并且我们希望将此特定图放置在第一列的第一行中。 类似地，212 表示将图放在第一列的第二行上。 请参考以下图表以及本书代码包的Chapter03文件夹中的solar_radiation.py文件：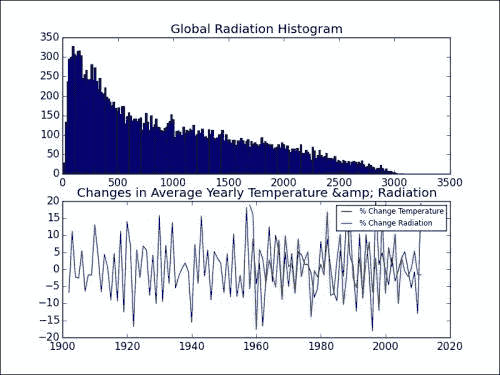

   

分析风向

风是由于大气压力的不同而使空气的运动。 KNMI De Bilt 数据文件具有一列以度为单位的向量平均风向（360 =北方，90 =东方，180 =南方，270 =西方，0 =平静/可变）。 我们将绘制该数据的直方图，并计算每个风向的相应平均温度。 预期风的产生方向会影响温度似乎是合理的。 换句话说，某些位置趋向于变暖或变冷，因此从那里散发出的空气将分别变暖或变冷。 您可能知道，荷兰没有任何山脉，因此我们不必考虑到这一点。 我们必须提醒自己北海的临近。 荷兰的海洋气候温和，西南风。 我们可以按照以下过程来研究风向信息：

1. 我们将风向和平均温度加载到 NumPy 数组中。 风向缺少值，因此需要进行一些转换。 我们将根据风向值创建一个遮罩数组：

   to_float = lambda x: float(x.strip() or np.nan)
   wind_direction, avg_temp = np.loadtxt(sys.argv[1], delimiter=',', usecols=(2, 11), unpack=True, converters={2: to_float})
   wind_direction = ma.masked_invalid(wind_direction)
   

2. 通过遍历每个可能的风向，找到相应的温度值，然后将它们平均，可以按照计算年均值的方式对风向求平均：

   avgs = []
   
   for direction in xrange(360):
      indices = np.where(direction == wind_direction)
      avgs.append(avg_temp[indices].mean())
   

3. 现在，我们将绘制风向直方图和每个风向的平均温度，如下所示：

   plt.subplot(211)
   plt.title("Wind Direction Histogram")
   plt.hist(wind_direction.compressed(), 200)
   
   plt.subplot(212)
   plt.title("Average Temperature vs Wind Direction")
   plt.plot(np.arange(360), avgs)
   plt.show()
   

   结果得到以下图。 注意直方图中与西南风向相对应的峰值。 平均温度似乎在 50 度左右触底。

   

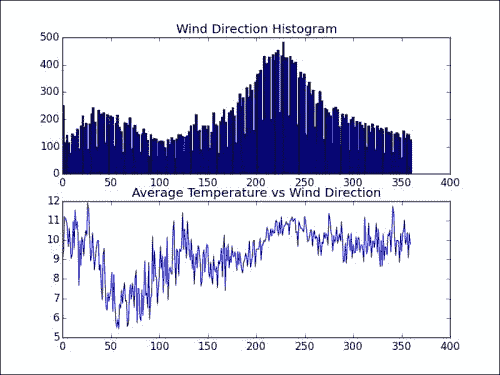
分析风速

风速是非常重要的值。 KNMI De Bilt 数据文件还具有以米/秒表示的每日平均风速数据。

我们将将风向，风速和平均温度加载到 NumPy 数组中。 风向和风速缺少值，因此需要进行一些转换。 我们将根据风向和风速值创建一个遮罩数组：

to_float = lambda x: float(x.strip() or np.nan)
wind_direction, wind_speed, avg_temp = np.loadtxt(sys.argv[1], delimiter=',', usecols=(2, 4, 11), unpack=True, converters={2: to_float, 4: to_float})
wind_direction = ma.masked_invalid(wind_direction)
wind_speed = ma.masked_invalid(wind_speed)
print "# Wind Speed values", len(wind_speed.compressed())
print "Min speed", wind_speed.min(), "Max speed", wind_speed.max()
print "Average", wind_speed.mean(), "Std. Dev", wind_speed.std()

print "Correlation of wind speed and temperature", np.corrcoef(avg_temp[~wind_speed.mask], wind_speed.compressed())[0][1]

提示

我们将查看风速的常规统计信息-最小值，最大值，平均值，标准差以及与平均温度的相关性。 注意，为了进行相关计算，我们需要将平均温度值与有效风速值进行匹配。 我们通过否定风速数组的遮罩来做到这一点，为我们提供有效值的索引。

在输出中，我们看到风速和温度之间的弱负相关性如下：

## Wind Speed values 39871 
Min speed 0.0 
Max speed 16.5 
Average 4.2211381706 
Std. Dev 1.93906822268 
Correlation of wind speed and temperature -0.126166541437

分析降水和日照时间

KNMI De Bilt 数据文件的列包含 0.1 小时内的降雨持续时间值。 日照时间（也以 0.1 小时给出）是根据全球辐射值得出的。 注意单词“全球”，而不是“太阳”。 因此，这里考虑了其他辐射源，但是目前细节并不十分重要。 我们将绘制降水持续时间值的直方图。 但是，我们将忽略没有降雨的日子，因为干旱的日子太多了，它会使整体情况发生变化。 我们还将显示每月平均降水量和日照时间。 以下步骤描述了降雨和日照长度的研究：

1. 我们将转换为月份，日照和降水持续时间的日期加载到 NumPy 数组中。 同样，我们将缺失值转换为 NaN。 代码如下：

   to_float = lambda x: float(x.strip() or np.nan)
   to_month = lambda x: dt.strptime(x, "%Y%m%d").month
   months, sun_hours, rain_hours = np.loadtxt(sys.argv[1], delimiter=',', usecols=(1, 18, 21), unpack=True, converters={1: to_month, 18: to_float, 21: to_float})
   

2. 在计算降水持续时间的基本统计量之前，我们将为日照和降雨持续时间创建遮罩数组。 有一个小细节需要注意。 由于某种原因，低的日照时间值记为 -1。 我决定将这些值转换为 0。 最好完全忽略它们。 代码如下：

   # Measurements are in .1 hours 
   rain_hours = .1 * ma.masked_invalid(rain_hours)
   
   #Get rid of -1 values
   print "# -1 values Before", len(sun_hours[sun_hours == -1])
   sun_hours[sun_hours == -1] = 0
   print "# -1 values After", len(sun_hours[sun_hours == -1])
   sun_hours = .1 * ma.masked_invalid(sun_hours)
   
   print "# Rain hours values", len(rain_hours.compressed())
   print "Min Rain hours ", rain_hours.min(), "Max Rain hours", rain_hours.max()
   print "Average", rain_hours.mean(), "Std. Dev", rain_hours.std()
   

   这将输出以下输出：

   # -1 values Before 832 
   # -1 values After 0 # Rain hours values 30373 
   Min Rain hours 0.0 
   Max Rain hours 24.0 
   Average 1.65149639482 
   Std. Dev 2.78643269679
   
   

   如预期的那样，降雨时间可以在 0 到 24 小时之间（或整天）。

3. 我们可以轻松地对数月内的日照和降水持续时间值进行平均。 首先，我们创建一个数月的数值范围。 其次，我们找到对应于每个月的数组索引。 然后，我们使用索引来选择持续时间值。 代码如下：

   monthly_rain = []
   monthly_sun = []
   month_range = np.arange(int(months.min()), int(months.max()))
   
   for month in month_range:
      indices = np.where(month == months)
      monthly_rain.append(rain_hours[indices].mean())
      monthly_sun.append(sun_hours[indices].mean())
   

4. 干旱天的数量非常多，因此我们将在降水持续时间直方图中将其忽略。 我们将绘制平均每月降雨和日照时间的条形图。 这里使用cal模块来显示图中的月份缩写名称。 代码如下：

   plt.subplot(211)
   plt.title("Precipitation Duration Histogram")
   plt.hist(rain_hours[rain_hours > 0].compressed(), 200)
   
   width = 0.42
   ax = plt.subplot(212)
   plt.title("Monthly Precipitation Duration")
   plt.bar(month_range, monthly_rain, width, label='Rain Hours')
   plt.bar(month_range + width, monthly_sun, width, color='red', label='Sun Hours')
   plt.legend()
   ax.set_xticklabels(cal.month_abbr[::2])
   ax.set_ylabel('Hours')
   plt.show()
   

   这为我们提供了以下令人兴奋的绘图：

   

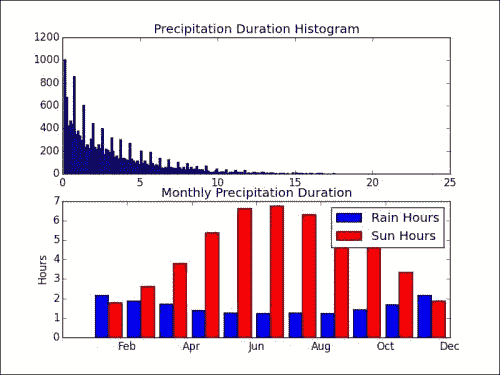
似乎日照与降水持续时间成反比。 因此，根据该系列中的先前证据，必须与温度成反比。 我们将其作为练习留给读者检查。 显然，降雨时间限制在 0 到 24 小时之间，较低的值更有可能出现。 我们可以清楚地看到，在夏季的几个月中，太阳的照射时间更长，而雨量则更少（持续时间较长）。 对于其他季节也可以得出类似的结论。

分析 De Bilt 的每月降水

让我们以来查看距 KNMI 0.1 毫米的 De Bilt 降水数据。 他们再次使用表示低值的 -1 约定。 我们将再次将这些值设置为 0：

1. 我们将将转换为月份，降雨数量和降雨持续时间（以小时为单位）的日期加载到 NumPy 数组中。 同样，缺少的值需要转换为 NaN。 然后，我们为缺少值的 NumPy 数组创建遮罩数组。 代码如下：

   to_float = lambda x: float(x.strip() or np.nan)
   to_month = lambda x: dt.strptime(x, "%Y%m%d").month
   months, duration, rain = np.loadtxt(sys.argv[1], delimiter=',', usecols=(1, 21, 22), unpack=True, converters={1: to_month, 21: to_float, 22: to_float})
   
   # Remove -1 values
   rain[rain == -1] = 0
   
   # Measurements are in .1 mm 
   rain = .1 * ma.masked_invalid(rain)
   
   # Measurements are in .1 hours 
   duration = .1 * ma.masked_invalid(duration)
   

2. 我们可以计算一些简单的统计量，例如最小值，最大值，平均值，标准差以及与降水持续时间的相关性。 最后一部分有些棘手，因为我们需要匹配有效值。 降水和降水持续时间的某个日期的值必须有效。 幸运的是，如果我们为数组的遮罩定义布尔条件，这将非常容易。 代码如下：

   print "# Rain values", len(rain.compressed())
   print "Min Rain mm ", rain.min(), "Max Rain mm", rain.max()
   print "Average", rain.mean(), "Std. Dev", rain.std()
   
   mask = ~duration.mask & ~rain.mask
   print "Correlation with duration", np.corrcoef(duration[mask], rain[mask])[0][1]
   

   前面的代码段显示以下值：

   # Rain values 39139 
   Min Rain mm 0.0 
   Max Rain mm 62.3 
   Average 2.17747770766 
   Std. Dev 4.33715191714 
   Correlation with duration 0.779006349536
   
   

降水量与降雨持续时间的相关性不是很强，但仍然是迄今为止我们在该系列中看到的最强的相关性。 作者相信，这两个变量是独立测量的，与阳光持续时间不同，后者是从全球辐射得出的。

分析 De Bilt 的大气压力

大气压是大气中空气施加的压力。 定义为力除以面积。 KNMI De Bilt 数据文件具有 0.1 hPa 的测量值，用于平均，最小和最大日压力。 我们将绘制平均压力和每月最小值，最大值和平均值的直方图：

1. 我们将转换为月，平均，最小和最大压力的日期加载到 NumPy 数组中。 同样，缺少的值需要转换为 NaN。 代码如下：

   to_float = lambda x: 0.1 * float(x.strip() or np.nan)
   to_month = lambda x: dt.strptime(x, "%Y%m%d").month
   months, avg_p, max_p, min_p = np.loadtxt(sys.argv[1], delimiter=',', usecols=(1, 25, 26, 28), unpack=True, converters={1: to_month, 25: to_float, 26: to_float, 28: to_float})
   

2. 压力值列中缺少值，因此我们必须从 NumPy 数组中创建遮罩数组。 以下代码段显示一些简单的统计量：

   max_p = ma.masked_invalid(max_p)
   print "Maximum Pressure", max_p.max()
   
   avg_p = ma.masked_invalid(avg_p)
   print "Average Pressure", avg_p.mean(), "Std Dev", avg_p.std()
   
   min_p = ma.masked_invalid(min_p)
   print "Minimum Pressure", min_p.max()
   

   此代码段输出以下值：

   Maximum Pressure 1050.4 
   Average Pressure 1015.14058231 Std Dev 9.85889134337 
   Minimum Pressure 1045.1
   
   

3. 您可以使用以下代码计算每月的平均值，最小值和最大值：

   monthly_pressure = []
   maxes = []
   mins = []
   month_range = np.arange(int(months.min()), int(months.max()))
   
   for month in month_range:
      indices = np.where(month == months)
      monthly_pressure.append(avg_p[indices].mean())
      maxes.append(max_p[indices].max())
      mins.append(min_p[indices].min())
   

4. 我们将绘制平均每日压力和相关的高斯曲线的直方图。 此外，我们将绘制上一步中准备的每月汇总值。 代码如下：

   plt.subplot(211)
   plt.title("Pressure Histogram")
   a, bins, b = plt.hist(avg_p.compressed(), 200, normed=True)
   stdev = avg_p.std()
   avg = avg_p.mean()
   plt.plot(bins, 1/(stdev * np.sqrt(2 * np.pi)) * np.exp(- (bins - avg)**2/(2 * stdev**2)), 'r-')
   
   ax = plt.subplot(212)
   plt.title("Monthly Pressure")
   plt.plot(month_range, monthly_pressure, 'bo', label="Average")
   plt.plot(month_range, maxes, 'r^', label="Maximum Values")
   plt.plot(month_range, mins, 'g>', label="Minimum Values")
   ax.set_xticklabels(cal.month_abbr[::2])
   plt.legend(prop={'size':'x-small'}, loc='best')
   ax.set_ylabel('hPa')
   plt.show()
   

   产生以下图：

   

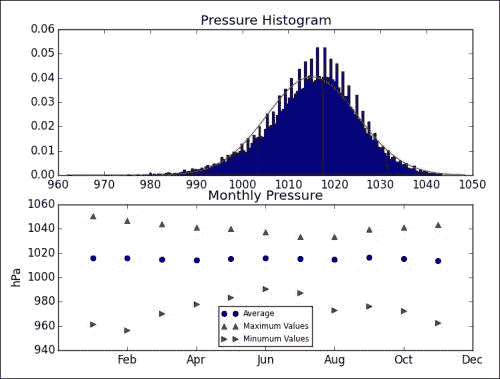
如您所见，钟形曲线几乎完美地拟合了平均每日压力的分布。 的月平均压力似乎是恒定的。

分析 De Bilt 的大气湿度

相对大气湿度是大气中相同温度下最大水蒸气分压的百分比。 在夏季，高湿度可能会导致出汗而消除多余的热量。 湿度还与降雨，露水和雾有关。 KNMI De Bilt 数据文件提供有关百分比的每日相对平均，最小和最大湿度的数据。 我们将绘制每日相对平均湿度和每月图表的直方图：

1. 我们将转换为月的日期，每日相对平均湿度以及最小和最大湿度加载到 NumPy 数组中。 同样，缺少的值需要转换为 NaN：

   to_float = lambda x: float(x.strip() or np.nan)
   to_month = lambda x: dt.strptime(x, "%Y%m%d").month
   months, avg_h, max_h, min_h = np.loadtxt(sys.argv[1], delimiter=',', usecols=(1, 35, 36, 38), unpack=True, converters={1: to_month, 35: to_float, 36: to_float, 38: to_float})
   

2. 相对湿度值列中缺少值，因此我们必须从 NumPy 数组中创建遮罩数组。 以下代码段显示一些简单的统计量：

   max_h = ma.masked_invalid(max_h)
   print "Maximum Humidity", max_h.max()
   
   avg_h = ma.masked_invalid(avg_h)
   print "Average Humidity", avg_h.mean(), "Std Dev", avg_h.std()
   
   min_h = ma.masked_invalid(min_h)
   print "Minimum Humidity", min_h.min()
   

   打印的统计数据如下：

   Maximum Humidity 111.0 
   Average Humidity 81.6147091109 Std Dev 10.3747295063 
   Minimum Humidity 8.0
   
   

   最大相对湿度在 100 以上，这很奇怪。 我们将绘制相对平均每日湿度的直方图。 此外，我们将绘制每月的汇总值（请参考本书代码包Chapter03文件夹中的atmospheric_humidity.py文件）。 结果将得到以下图：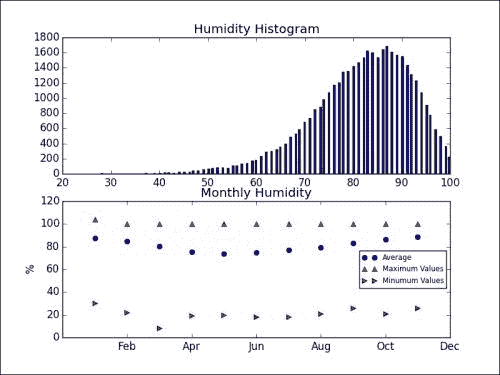

   

最大值正在发生奇怪的事情。 他们似乎高于 100%。 也许作者误解了相对湿度的定义。 但是，相对平均湿度值似乎在 0-100% 之间。

总结

本章介绍了大量常见的 NumPy 函数。 我们探索了 KNMI 气象站的数据。 探索不是详尽无遗的，因此我鼓励您自己使用数据。 您应该已经意识到，使用 NumPy 和相关的 Python 库进行基本数据分析是多么容易。

在下一章中，我们将更进一步，并尝试使用相同的数据预测温度。

四、使用 NumPy 的简单预测性分析

在上一章探索了气象数据之后，我们现在将尝试预测温度。 通常，天气预测是通过复杂的模型和顶级的超级计算机来完成的。 大多数人无法访问这些资源，因此我们会偷工减料并使用更简单的模型。 本章涵盖的主题列表如下：

• 自相关
• 自回归模型
• 可靠的统计量

使用 Pandas 检查平均温度的自相关

Pandas（Python 数据分析）库只是 NumPy，Matplotlib， 和其他 Python 库。 您可以在 Pandas 网站上找到更多信息，包括安装说明。 大多数良好的 API（例如 NumPy）似乎都遵循 Unix 的哲学-保持简单并做一件事。 这种理念产生了许多小型工具和工具，这些工具可以用作更大对象的构建块。 Pandas 库在其方法中模仿 R 编程语言。

pandas 库具有绘图子例程，可以绘制滞后图和自相关图。 自相关是数据集中的相关性，可以指示趋势。 例如，如果我们有一天的延迟，我们可以查看昨天的平均温度是否会影响今天的温度。 对于这种情况，自相关值需要相对较高。

Pandas 也可以用于重新采样数据。 现在让我们学习如何对 De Bilt 数据的每日平均温度进行重新采样以得出年度平均值。

在以下代码段中，pd是指导入的 Pandas 模块。 我们将跳过数据的导入和加载（有关更多详细信息，请参见本书代码包的Chapter04文件夹中的pandas_plots.py文件）。 现在，让我们借助以下步骤来绘制滞后数据：

1. 从日期列表中创建DatetimeIndex对象：

   dtidx = pd.DatetimeIndex([dt.fromordinal(int(date)) for date in dates])
   

2. 创建一个 PandasSeries数组，这是一个时间序列数组。 由于文件中记录温度的方式，我们必须将温度乘以 0.1：

   data = pd.Series(avg_temp * .1, index=dtidx)
   

3. 绘制滞后图，如下所示：

   lag_plot(data)
   

   获得以下滞后图，其中将时间序列中的下一个值y(t+1)相对于前一个值y(t)进行了绘制：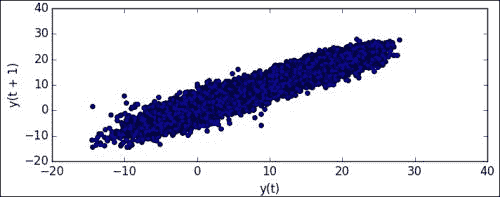

   

4. 绘制自相关如下：

   autocorrelation_plot(data)
   

   这可能会导致以下图表：

   

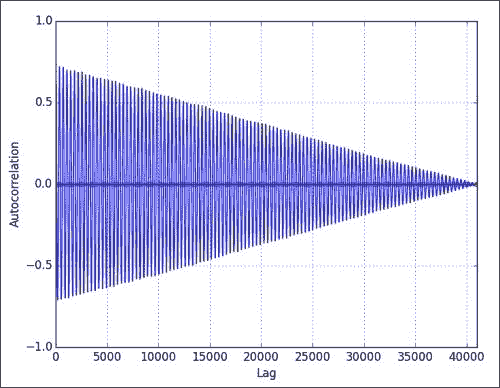
   如您所见，自相关下降的延迟更大。 这一点很重要，以后需要记住。

5. 重新采样为年度平均值（用A表示），并按以下方式绘制重新采样的数据：

   resampled = data.resample('A')
   resampled.plot()
   

   重新采样的图显示如下，其中年份与平均温度相对应：

   

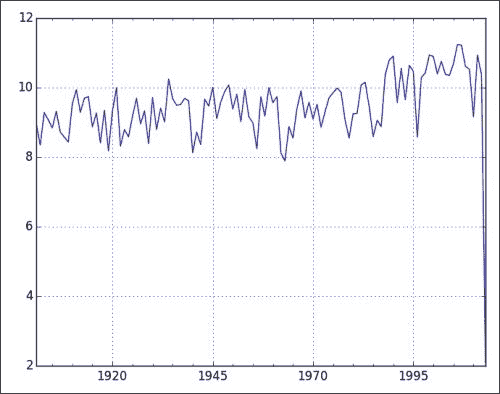
您可能会注意到，我们在上一章中使用纯 NumPy 进行了相同的重采样，这还需要更多工作。

使用 pandas 数据帧描述数据

幸运的是，Pandas 具有描述性的统计工具。 我们将从 KNMI De Bilt 数据文件中读取平均风速，温度和压力值到 Pandas 数据帧中。 该对象类似于 R 数据框，它类似于电子表格或数据库中的数据表。 列被标记，可以为数据建立索引，并且您可以对数据进行计算。 然后，我们将打印出描述性统计数据和相关矩阵，如以下步骤所示：

1. 使用 Pandas read_csv函数读取 CSV 文件。 此函数的工作方式类似于 NumPy load_txt函数：

   to_float = lambda x: .1 * float(x.strip() or np.nan)
   to_date = lambda x: dt.strptime(x, "%Y%m%d")
   cols = [4, 11, 25]
   conv_dict = dict( (col, to_float) for col in cols) 
   
   conv_dict[1] = to_date
   cols.append(1)
   
   headers = ['dates', 'avg_ws', 'avg_temp', 'avg_pres']
   df = pd.read_csv(sys.argv[1], usecols=cols, names=headers, index_col=[0], converters=conv_dict)
   

2. 使用下表中描述的函数打印描述性统计量：

   函数	描述
   head	这类似于head Unix 命令，并选择DataFrame的第一条记录。
   tail	这类似于tail Unix 命令，并选择DataFrame的最后一条记录
   describe	这将计算一些预定义的描述性统计信息
   corr	计算相关矩阵

   代码如下：

   print df.head()
   print
   
   print df.tail()
   print
   
   print df.describe()
   print
   
   print df.corr()
   

   输出如下：

   

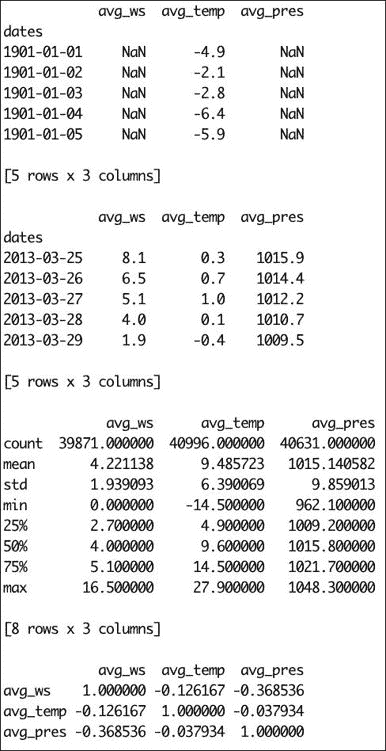
使用 Pandas 将天气和股价相关联

我们将尝试将荷兰的股票市场数据与我们上一次根据 KNMI De Bilt 气象数据生成的数据框进行关联。 作为股票市场的代理，我们将使用 EWN ETF 的收盘价。 顺便说一句，这可能不是最佳选择，因此，如果您有更好的主意，请使用适当的股票报价器。 此练习的步骤如下：

1. 从 Yahoo 财经下载具有特殊特征的 EWN 数据。 代码如下：

   #EWN start Mar 22, 1996
   start = dt(1996, 3, 22)
   end = dt(2013, 5, 4)
   
   symbol = "EWN"
   quotes = finance.quotes_historical_yahoo(symbol, start, end, asobject=True)
   

2. 使用下载的数据中的可用日期创建一个DataFrame对象：

   df2 = pd.DataFrame(quotes.close, index=dt_idx, columns=[symbol])
   

3. 将新的数据帧对象与天气数据的数据帧结合在一起。 然后，我们将获得相关矩阵：

   df3 = df.join(df2)
   
   print df3.corr()
   

   相关矩阵如下：

   

如您所见，股价与天气参数之间的相关性非常弱。

预测温度

温度是热力学变量，量化为热还是冷。 为了预测温度，我们可以运用热力学和气象学的知识。 通常，这将导致创建具有大量输入的复杂天气模型。 但是，这超出了本书的范围，因此我们将尝试使我们继续的示例保持简单和可管理。

滞后 1 的自回归模型

明天的温度是多少？ 可能与今天相同，但有所不同。 我们可以假设温度是前一天温度的函数。 这可以通过我们之前创建的自相关图来证明。 为简单起见，我们将进一步假设该函数是多项式。 我们将定义一个用于拟合的截止点。 应将 90% 的数据用于此目的。 让我们用 NumPy 为这个想法建模：

1. 使用polyfit函数将数据拟合为不同次数的多项式，如以下代码行所示：

   poly = np.polyfit( avg_temp[: cutoff - 1], avg_temp[1 : cutoff], degree)
   

2. 根据上一步获得的多项式计算值。 在这里，我们使用剩余的 10% 的数据。 代码如下：

   fit = np.polyval(poly, avg_temp[cutoff:-1])
   

3. 计算实际温度和预测温度之间的绝对差：

   delta = np.abs(avg_temp[cutoff + 1:] - fit)
   

4. 对于每个多项式拟合，计算出的增量百分比在 1、2 或 3 摄氏度误差范围内，如以下屏幕截图所示：

   

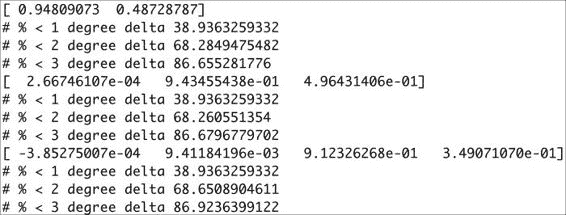
如您所见，高阶多项式的精度几乎与一阶多项式相同。

滞后 2 的自回归模型

从理论上回顾两天，可以使我们的模型更准确。 但是，由于与滞后 2 相关的自相关不是那么强，因此无法保证。 在 NumPy 中，我们有几种方法来建立模型。 在这里，我选择使用lstsq函数来执行此操作。 我们对滞后 1 和滞后 2 分量假定某种线性组合，然后应用线性回归。 该方法可以延长较长的回溯期，但现在暂时可以滞后 2。 此练习的步骤如下：

1. 设置一个矩阵A，并在其中输入滞后 2 和 1 直到截止点的值。 代码如下：

   A = np.zeros((2, cutoff - 2), float)
   
   A[0, ] = temp[:cutoff - 2]
   A[1, ] = temp[1 :cutoff - 1]
   

2. 使用我们要拟合的值创建向量b：

   b = temp[2 : cutoff]
   

3. 求解方程Ax = b。 代码如下：

   (x, residuals, rank, s) = np.linalg.lstsq(A.T, b)
   print x
   

   滞后 1 和滞后 2 的系数打印如下：

   [-0.08293789  1.06517683]
   

4. 预测高于临界点的值：

   fit = x[0] * temp[cutoff-1:-2] + x[1] * temp[cutoff:-1]
   

5. 计算绝对误差：

   delta = np.abs(temp[cutoff + 1:] - fit)
   

6. 绘制绝对误差的直方图：

   plt.hist(delta, bins = 10, normed=True)
   

   绝对误差的直方图如下所示（请参考本书代码包Chapter04文件夹中的lag2.py文件）：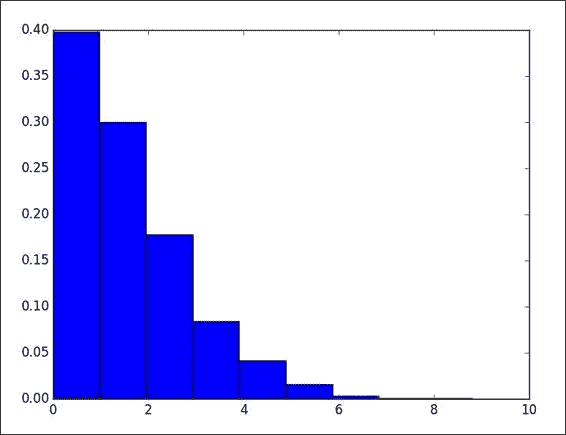

   

分析年内每日平均温度

我们将通过将日期转换为数字来表示年的对应天，从而来查看一年内的温度变化。 此数字介于 1 和 366 之间，其中 1 对应于 1 月 1 日，而 365（或 366）对应于 12 月 31 日。 执行以下步骤来分析年内日平均温度：

1. 初始化范围为 1-366 的数组，将平均值初始化为zeros：

   rng = np.arange(1, 366)
   avgs = np.zeros(365)
   avgs2 = np.zeros(365)
   

2. 在截止点之前和之后的一年中的一天之前计算平均值：

   for i in rng: 
      indices = np.where(days[:cutoff] == i)
      avgs[i-1] = temp[indices].mean()
      indices = np.where(days[cutoff+1:] == i)
      avgs2[i-1] = temp[indices].mean()
   

3. 将截止点之前的平均值拟合为二次多项式（仅是一阶近似值）：

   poly = np.polyfit(rng, avgs, 2)
   print poly
   

   打印以下幂次幂的多项式系数：

   [ -4.91329859e-04   1.92787493e-01  -3.98075418e+00]
   
   

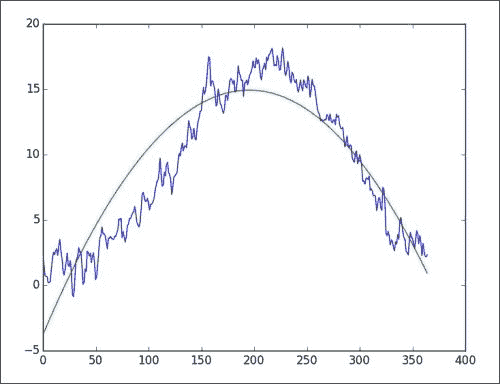
4. 绘制截止点之后的平均值，并使用我们获得的多项式显示拟合：

   plt.plot(avgs2)
   plt.plot(np.polyval(poly, rng))
   plt.show()
   

   正如您在下图中所看到的，拟合度很好，但并不完美。 正如您在夏天前后所观察到的那样，在年中，我们的气温最高。 一月和十二月，温度达到最低点。

   

年度温度模型简介

继续与我们在上一个示例中所做的工作一起，我想提出一个新模型，其中温度是一年中某一天（介于 1 和 366 之间）的的函数。 当然，该模型并不完整，但是可以用作更高级模型的组成部分，该模型应考虑我们对滞后 2 所做的先前自回归模型。该模型的过程如下所示：

1. 如上一节所述，将截止点之前的温度数据拟合为二次多项式，但不求平均值：

   poly = np.polyfit(days[:cutoff], temp[:cutoff], 2)
   print poly
   

   信不信由你，我们得到了与之前相同的多项式系数：

   [ -4.91072584e-04   1.92682505e-01  -3.97182941e+00]
   
   

2. 计算预测值与实际值之间的绝对差：

   delta = np.abs(np.polyval(poly, days[cutoff:]) - temp[cutoff:])
   

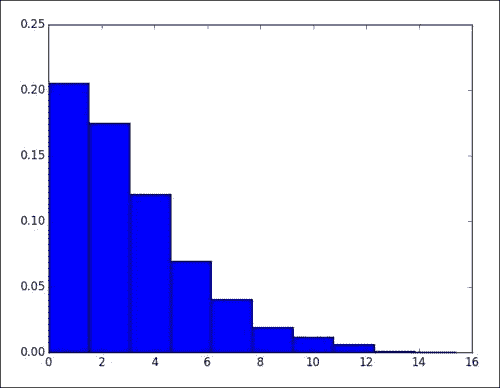
3. 绘制绝对误差的直方图：

   plt.hist(delta, bins = 10, normed = True)
   plt.show()
   

   请参考下图。 似乎我们用自回归模型得到了更好的结果。

   

使用 SciPy leastsq函数建模温度

因此，现在我们有两个想法：或者今天的温度取决于昨天和前天的温度，并且我们假设某种线性组合形成了，或者温度取决于一年中的一天（介于 1 到 366 之间）。 我们可以结合这些想法，但是问题是如何实现的。 看来我们可以有一个乘法模型或一个加法模型。

让我们选择加性模型，因为它看起来更简单。 这意味着我们假设温度是自回归成分和循环成分的总和。 将其写成一个方程式很容易。 我们将使用 SciPy leastsq函数来最小化此方程式误差的平方。 该模型的过程如下所示：

1. 定义一个计算模型误差的函数。 代码如下：

   def error(p, d, t, lag2, lag1):
      l2, l1, d2, d1, d0 = p
   
      return t - l2 * lag2 + l1 * lag1 + d2 * d ** 2 + d1 * d + d0
   

2. 对方程中的所有参数进行初步猜测：

   p0 = [-0.08293789,  1.06517683, -4.91072584e-04,   1.92682505e-01,  -3.97182941e+00]
   

   这里的值来自以前的程序，但是原则上您可以使用其他值，只要解决方案收敛得足够快即可。

3. 如以下代码行所示，应用leastsq函数：

   params = leastsq(error, p0, args=(days[2:cutoff], temp[2:cutoff], temp[:cutoff - 2], temp[1 :cutoff - 1]))[0]
   print params
   

4. 模型的最终参数如下打印。 看起来除第一个参数外的所有参数的绝对大小都已减小。 我不知道这是否是偶然的，但据我所知，参数的顺序无关紧要。

   [ -1.52297691e-01  -9.89195783e-01   8.20879954e-05  -3.16870659e-02    6.06397834e-01]
   
   

5. 然后，我们为在截止点以上应用的模型计算绝对误差，并绘制误差的直方图。 为了简洁起见，此处省略了该代码。

   请参考下图。 该模型的准确性似乎并不比具有滞后 2 的简单自回归模型更好。

   

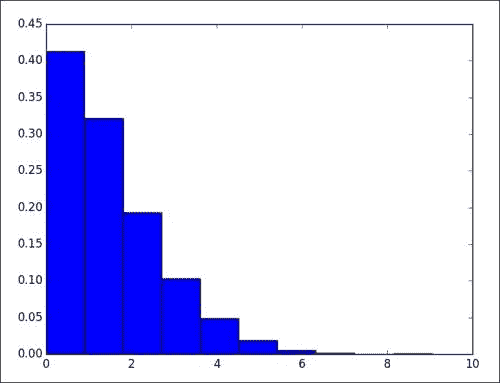
选取一年中的两个日期的温度

可以提高和逐年温度拟合的二次多项式近似。 到目前为止，我们尚未使用任何 NumPy 三角函数。 这些应该很适合这个问题。 因此，让我们尝试使用三角函数并再次使用scipy.optimize模块（准确地说是leastsq）中的函数进行拟合，如下所示：

1. 设置一个简单的model函数和一个要最小化的error函数，如以下代码片段所示：

   def model(p, d):
      a, b, w, c = p
      return a + b * np.cos(w * d + c)
   
   def error(p, d, t):
      return t - model(p, d)
   

2. 给出初步猜测并拟合数据：

   p0 = [.1, 1, .01, .01]
   params = leastsq(error, p0, args=(days, temp))[0]
   print params
   

   我们得到以下参数：

   [ 9.6848106  -7.59870042 -0.01766333 -5.83349705]
   
   

注意

此处，在 365 上的-2pi等于第三参数。 我相信第一个参数等于所有温度的平均值，我们可以对其他参数得出类似的解释。 计算一年中每一天的平均值，并绘制平均值和拟合值。 我们之前已经做过，因此省略了这部分代码。

我们在下图中得到拟合：

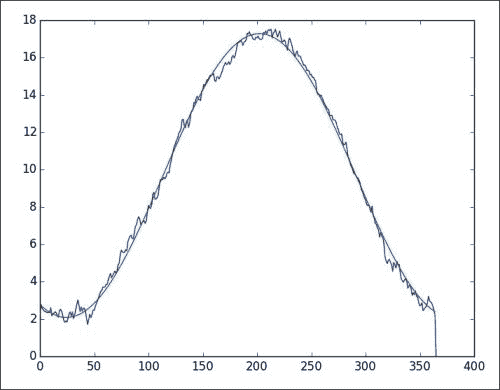
滞后 1 的移动平均温度模型

时间序列的移动平均模型将数据表示为围绕数据均值的振荡。 假定滞后分量是白噪声（据我所知，这不是一个政治上不正确的术语），它形成线性组合。 我们将再次使用leastsq函数来拟合模型：

1. 我们将从一个简单的移动平均模型开始。 它只有一个滞后分量，因此只有一个系数。 代码段如下：

   def model(p, ma1):
      return p * ma1
   

2. 调用leastsq函数。 在这里，我们从数据中减去平均值：

   params = leastsq(error, p0, args=(temp[1:cutoff] - mu, temp[:cutoff-1] - mu))[0]
   print params
   

   程序打印以下参数：

   [ 0.94809073]
   
   

   我们得到以下绝对误差直方图图，该图可与自回归模型结果进行比较：

   

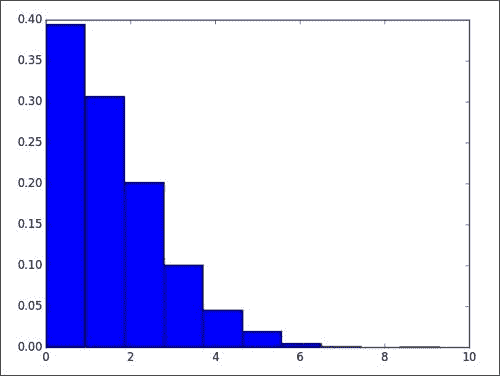
自回归移动平均温度模型

自回归移动平均值（ARMA）模型混合了自回归（AR）和移动平均线（MA） 楷模。 我们已经讨论了这两种模型。 非正式地说，我们可以说自回归分量周围带有白噪声。 可以将这种白噪声的一部分建模为滞后分量加上一些常数的线性组合，如下所示：

1. 使用我们从上一个脚本获得的线性系数，定义滞后 2 的自回归模型：

   def ar(a):
      ar_p = [1.06517683, -0.08293789]
   
      return ar_p[0] * a[1:-1] + ar_p[1] * a[:-2]
   

2. 定义滞后 1 的移动平均模型：

   def model(p, ma1):
      c0, c1 = p
   
      return c0 + c1 * ma1
   

3. 从数据中减去自回归模型值，得出误差项（白噪声）：

   err_terms = temp[cutoff+1:] - ar(temp[cutoff-1:])
   

   该模型的大多数代码对您来说应该看起来很熟悉，如以下代码所示：

   import sys
   import numpy as np
   import matplotlib.pyplot as plt
   from datetime import datetime as dt
   from scipy.optimize import leastsq
   
   temp = .1 * np.loadtxt(sys.argv[1], delimiter=',', usecols=(11,), unpack=True)
   cutoff = 0.9 * len(temp)
   
   def model(p, ma1):
      c0, c1 = p
   
      return c0 + c1 * ma1
   
   def error(p, t, ma1):
      return t - model(p, ma1)
   
   p0 = [.1, .1]
   
   def ar(a):
      ar_p = [1.06517683, -0.08293789]
   
      return ar_p[0] * a[1:-1] + ar_p[1] * a[:-2]
   
   err_terms = temp[2:cutoff] - ar(temp[:cutoff])
   params = leastsq(error, p0, args=(err_terms[1:], err_terms[:-1]))[0]
   print params
   
   err_terms = temp[cutoff+1:] - ar(temp[cutoff-1:])
   delta = np.abs(error(params, err_terms[1:], err_terms[:-1]))
   print "% delta less than 2", (100\. * len(delta[delta <= 2]))/len(delta)
   
   plt.hist(delta, bins = 10, normed = True)
   plt.show()
   

   脚本的输出如下：

   [ 0.16506278  0.01041355] 
   % delta less than 2 69.7169350903
   
   

时变温度均值的调整自回归模型

这是一个大嘴巴，但听起来并不像那样复杂。 让我们在以下几点分析标题：

• 我们发现，一年中每一天的平均温度似乎都符合一年的周期。 这可能与地球绕太阳旋转有关。
• 似乎有温度升高的趋势。 有人称其为全球变暖和怪罪行业以及人类。 在不进行政治讨论的情况下，我们假定此主张中存在真理。 此外，让我们现在假设这种趋势取决于年份。 我知道我会为此感到麻烦，但现在我们也假设该关系基于一次多项式（一条直线）。
• 为了争辩，让我们声明前两点共同构成一个时间相关的均值。 我们将剩余的东西建模为自回归滞后分量的线性组合。

我们需要执行以下步骤来建立和创建模型：

1. 为年份，年份和温度创建数组。

2. 平均一年中每一天的温度。

3. 从上一步中的值中减去当日平均值。

4. 将余数拟合为一条直线，然后从余数中减去拟合值。

5. 对滞后为 2 的自回归模型进行最小二乘拟合。

   根据该模型预测温度并绘制绝对误差图。

该代码很简单，给出如下：

import sys
import numpy as np
import matplotlib.pyplot as plt
from datetime import datetime as dt
from scipy.optimize import leastsq

to_ordinal = lambda x: dt.strptime(x, "%Y%m%d").toordinal()
ordinals, temp = np.loadtxt(sys.argv[1], delimiter=',', usecols=(1, 11), unpack=True, converters={1: to_ordinal})
days = np.array([dt.fromordinal(int(d)).timetuple().tm_yday for d in ordinals])
years = np.array([dt.fromordinal(int(d)).year for d in ordinals])
temp = .1 * temp
cutoff = 0.9 * len(temp)

avgs = np.zeros(366)

for i in xrange(1, 366):
   indices = np.where(days[:cutoff] == i)
   avgs[i-1] = temp[indices].mean()

def subtract_avgs(a, doy):
   return a - avgs[doy.astype(int)-1]

def subtract_trend(a, poly, b):
   return a - poly[0] * b - poly[1]

def print_stats(a):
   print "Min", a.min(), "Max", a.max(), "Mean", a.mean(), "Std", a.std()
   print

## Step 1\. DOY avgs
less_avgs = subtract_avgs(temp[:cutoff], days[:cutoff])
print "After Subtracting DOY avgs"
print_stats(less_avgs)

## Step 2\. Linear trend
trend = np.polyfit(years[:cutoff], less_avgs, 1)
print "Trend coeff", trend
less_trend = subtract_trend(less_avgs, trend, years[:cutoff])
print "After Subtracting Linear Trend"
print_stats(less_trend)

def model(p, lag2, lag1):
   l1, l2 = p

   return l2 * lag2 + l1 * lag1

def error(p, t, lag2, lag1):
   return t - model(p, lag2, lag1) 

p0 = [1.06517683, -0.08293789]
params = leastsq(error, p0, args=(less_trend[2:], less_trend[:-2], less_trend[1:-1]))[0]
print "AR params", params

##Step 1\. again
less_avgs = subtract_avgs(temp[cutoff+1:], days[cutoff+1:])

##Step 2\. again
less_trend = subtract_trend(less_avgs, trend, years[cutoff+1:])

delta = np.abs(error(params, less_trend[2:], less_trend[:-2], less_trend[1:-1]))
print "% delta less than 2", (100\. * len(delta[delta <= 2]))/len(delta)

plt.hist(delta, bins = 10, normed = True)
plt.show()

打印以下输出：

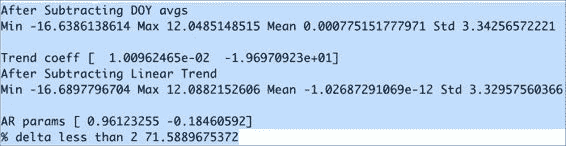
De Bilt 平均温度的异常值分析

离群值是数据集中的值，被认为是极值。 离群值可能是由测量或其他类型的错误引起的，也可能是由自然现象引起的。 离群值有几种定义。 在此示例中，我们将使用使用轻微异常值的定义。 此定义取决于第一和第三四分位数的位置。 数据集中项目的四分之一和四分之三分别小于第一和第三四分位数的值。 这些特定四分位数之间的差异称为四分位数间距。 这是一种类似于标准差的强大色散测量方法。 轻度离群值的定义是与第一个或第三个四分位数相差 1.5 个四分位数。 我们可以如下研究温度异常值：

1. 使用 SciPy 的函数查找第一个四分位数：

   q1 = scoreatpercentile(temp, 25)
   

2. 找到第三个四分位数：

   q3 = scoreatpercentile(temp, 75)
   

3. 查找温和异常值的下标：

   indices = np.where(temp < (q1 - N * irq))
   

4. 绘制索引（显示聚类）和离群值的差异：

   plt.subplot(211)
   plt.plot(np.diff(indices)[0])
   plt.title('Indices Diff')
   plt.subplot(212)
   plt.title('Outliers Temperature')
   plt.plot(outliers)
   plt.show()
   

以下 NumPy 代码分析异常值，并尝试找出是否发生异常值的聚类：

import sys
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import scoreatpercentile
from datetime import datetime as dt

to_ordinal = lambda x: dt.strptime(x, "%Y%m%d").toordinal()
ordinals, temp = np.loadtxt(sys.argv[1], delimiter=',', usecols=(1, 11), unpack=True, converters={1: to_ordinal})
temp = .1 * temp
q1 = scoreatpercentile(temp, 25)
print "1st Quartile", q1
q3 = scoreatpercentile(temp, 75)
print "3rd Quartile", q3
irq = q3 - q1
print "Std", temp.std(), "IRQ", irq
N = 1.5 
print len(temp[temp > (q3 + N * irq)])
indices = np.where(temp < (q1 - N * irq))

outliers =  temp[indices]
print "#Outliers", len(outliers)
plt.subplot(211)
plt.plot(np.diff(indices)[0])
plt.title('Indices Diff')
plt.subplot(212)
plt.title('Outliers Temperature')
plt.plot(outliers)
plt.show()

显然，离群值位于较冷的一侧，如以下输出所示：

下图显示了一些聚类，但据我所知没有规则的模式：

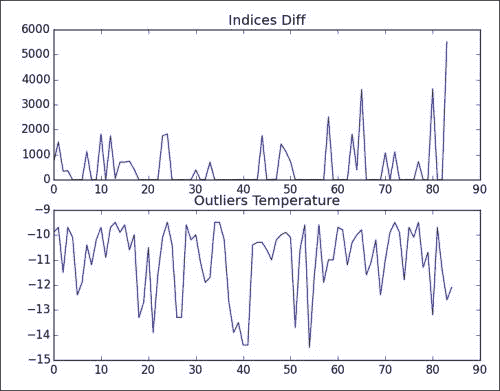
使用更强大的统计量

我们可以通过执行以下操作，使来自“时间相关的温度均值的调整的自回归模型”部分的代码更可靠：

• 计算中位数而不是平均值

  avgs[i-1] = np.median(temp[indices])
  

• 使用遮罩数组忽略异常值

  temp[:cutoff] = ma.masked_array(temp[:cutoff], temp[:cutoff] < (q1 - 1.5 * irq))
  

使用修改后的代码，我们得到的输出会略有不同，预测值的大约 70% 的绝对误差小于 2 摄氏度：

AR params [ 0.95095073 -0.17373633]
% delta less than 2 70.8567244325

总结

在本章中，我们学习了几种简单的温度预测技术。 当然，他们还不具备可以使用超级计算机并可以应用复杂方程式的气象学家水平。 但是我们的简单方法确实取得了很大的进步。

在下一章中，我们将切换到不同的数据集。 下一章将重点介绍信号处理技术。

五、信号处理技术

我们将在本章中学习一些信号处理技术，并使用这些技术来分析时序数据。 作为示例数据，我们将使用比利时科学研究所提供的黑子数据。 我们可以从互联网上的多个位置下载此数据，并且statsmodels库也将其作为示例数据提供。 我们可以对数据做很多事情，例如：

• 试图确定数据中的周期性周期。 可以做到，但这有点高级，所以我们将帮助您入门。
• 平滑数据以过滤噪声。
• 预测。

太阳黑子数据简介

太阳黑子是在太阳表面可见的黑点。 天文学家已经对这种现象进行了数百年的研究。 已经发现周期性黑子周期的证据。 我们可以从这里下载最新的年度黑子数据。 这是由比利时太阳能影响数据分析中心提供的。 数据可追溯到 1700 年，其中包含超过 300 个年平均值。 为了确定太阳黑子的周期，科学家成功地使用了 Hilbert-Huang 变换。 该变换的主要部分是所谓的经验模式分解（EMD）方法。 整个算法包含许多迭代步骤，在这里我们将仅介绍其中的一些步骤。 EMD 将数据缩减为一组本征模式函数（IMF）。 您可以将其与快速傅立叶变换将正弦和余弦项叠加的信号分解方式进行比较。

通过过滤过程完成的提取 IMF。 信号的过滤与一次分离一个信号的成分有关。 此过程的第一步是确定局部极值。 我们将执行第一步，并使用发现的极值绘制数据。 让我们以 CSV 格式下载数据。 在第 3 章，“使用 NumPy 进行基本数据分析”中，我们学习了如何将 CSV 文件加载到 NumPy 数组中，因此，如有必要，请返回阅读。 在那。 我们还需要反转数组以使其按正确的时间顺序排列（有关详细信息，请参阅第 2 章， “NumPy 基础知识”）。 以下代码段分别查找局部最小值和最大值的索引：

mins = signal.argrelmin(data)[0]
maxs = signal.argrelmax(data)[0]

现在我们需要连接这些数组，并使用索引选择相应的值。 以下代码完成了该任务并绘制了数据：

import numpy as np
import sys
import matplotlib.pyplot as plt
from scipy import signal

data = np.loadtxt(sys.argv[1], delimiter=',', usecols=(1,), unpack=True, skiprows=1) 
##reverse order
data = data[::-1]

mins = signal.argrelmin(data)[0]
maxs = signal.argrelmax(data)[0]
extrema = np.concatenate((mins, maxs))

year_range = np.arange(1700, 1700 + len(data))

plt.plot(1700 + extrema, data[extrema], 'go')
plt.plot(year_range, data)
plt.show()

我们将看到以下图表：

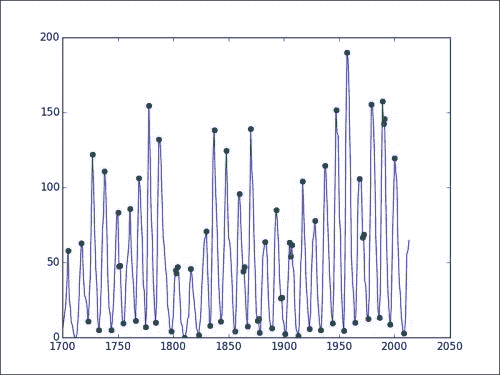
在该图中，您可以看到极点用点表示。

再谈过滤

过滤过程中的后续步骤要求我们对最小值和最大值的三次样条进行插值。 这将创建一个上信封和一个下信封，它们应包围数据。 EMD 处理的下一次迭代需要包络线的平均值。 我们可以使用以下代码片段对最小值进行插值：

spl_min = interpolate.interp1d(mins, data[mins], kind='cubic')
min_rng = np.arange(mins.min(), mins.max())
l_env = spl_min(min_rng)

可以使用类似的代码对最大值进行插值。 我们需要注意，插值结果仅在我们插值的范围内有效。 该范围由最小值/最大值的首次出现定义，并在最小值/最大值的最后出现时结束。 不幸的是，我们以这种方式定义的最大值和最小值的插值范围并不完全匹配。 因此，出于绘制目的，我们需要提取一个位于最大和最小插值范围内的较短范围。 看下面的代码：

import numpy as np
import sys
import matplotlib.pyplot as plt
from scipy import signal
from scipy import interpolate

data = np.loadtxt(sys.argv[1], delimiter=',', usecols=(1,), unpack=True, skiprows=1) 
##reverse order
data = data[::-1]

mins = signal.argrelmin(data)[0]
maxs = signal.argrelmax(data)[0]
extrema = np.concatenate((mins, maxs))

year_range = np.arange(1700, 1700 + len(data))
spl_min = interpolate.interp1d(mins, data[mins], kind='cubic')
min_rng = np.arange(mins.min(), mins.max())
l_env = spl_min(min_rng)

spl_max = interpolate.interp1d(maxs, data[maxs], kind='cubic')
max_rng = np.arange(maxs.min(), maxs.max())
u_env = spl_max(max_rng)

inclusive_rng = np.arange(max(min_rng[0], max_rng[0]), min(min_rng[-1], max_rng[-1]))
mid = (spl_max(inclusive_rng) + spl_min(inclusive_rng))/2

plt.plot(year_range, data)
plt.plot(1700 + min_rng, l_env, '-x')
plt.plot(1700 + max_rng, u_env, '-x')
plt.plot(1700 + inclusive_rng, mid, '--')
plt.show()

该代码产生以下图表：

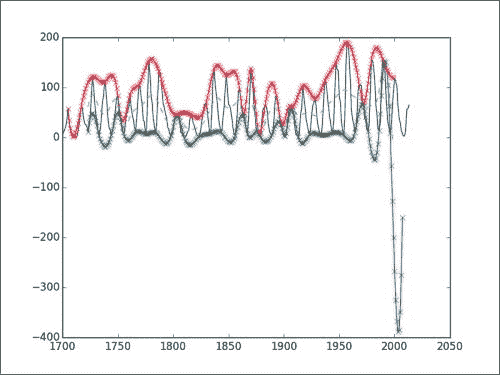
您将看到观察到的数据，其中包括计算出的包络线和中线。 显然，在这种情况下，负值没有任何意义。 但是，对于该算法，我们只需要关心上下包络的中线即可。 在前两个部分中，我们基本上执行了 EMD 过程的第一次迭代。 该算法涉及更多，因此无论您是否要自己继续进行此分析，我们都将由您决定。

移动平均线

移动平均值是常用的分析时间序列数据的工具。 移动平均线定义了一个以前查看过的数据的窗口，该窗口在每次向前滑动一个周期时将其平均。 不同类型的移动平均线在平均权重方面本质上有所不同。 例如，指数移动平均值的权重随时间呈指数下降。 这意味着较旧的值比较新的值具有较小的影响，这有时是理想的。

我们可以在 NumPy 代码中为简单移动平均线表示等权重策略：

weights = np.exp(np.linspace(-1., 0., N))
weights /= weights.sum()

一个简单的移动平均线使用相等的权重，该权重在代码中如下所示：

def sma(arr, n):
   weights = np.ones(n) / n

   return np.convolve(weights, arr)[n-1:-n+1]

以下代码绘制了 11 年和 22 年黑子周期的简单移动平均值：

import numpy as np
import sys
import matplotlib.pyplot as plt

data = np.loadtxt(sys.argv[1], delimiter=',', usecols=(1,),        
unpack=True, skiprows=1) 
##reverse order
data = data[::-1]

year_range = np.arange(1700, 1700 + len(data))

def sma(arr, n):
   weights = np.ones(n) / n

   return np.convolve(weights, arr)[n-1:-n+1]

sma11 = sma(data, 11)
sma22 = sma(data, 22)

plt.plot(year_range, data, label='Data')
plt.plot(year_range[10:], sma11, '-x', label='SMA 11')
plt.plot(year_range[21:], sma22, '--', label='SMA 22')
plt.legend()
plt.show()

在下图中，我们看到了 11 年和 22 年期的原始数据和简单移动平均线。 如您所见，移动平均线不适用于此数据。 对于正弦数据通常是这种情况。

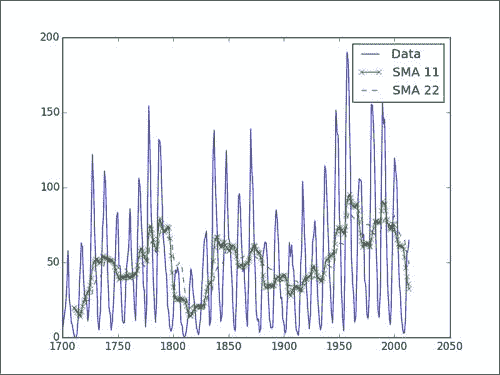
平滑函数

平滑可以帮助我们消除原始数据中的噪声和离群值。 例如，这使得更容易发现数据趋势。 NumPy 提供了许多平滑函数。

注意

这些函数可以像前面的示例一样在滑动窗口中计算权重。

除kaiser函数外，这些函数仅需要一个参数-窗口大小，对于黑子数据的中间周期，我们将其设置为 22。 kaiser函数还需要一个beta参数。 使用此参数，kaiser函数可以模仿其他函数。

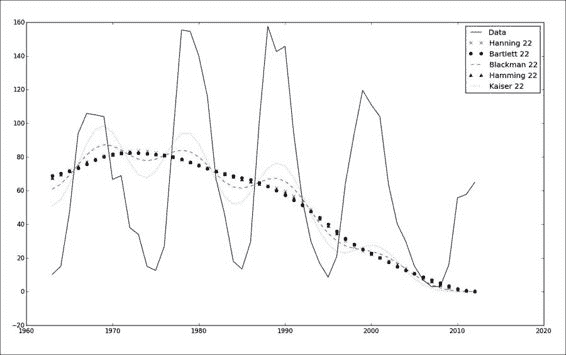
NumPy 文档建议beta参数的起始值为 14，这也是我们将要使用的值。 代码简单明了，给出如下（此处的数据仅限于最近 50 年，以方便在图中进行比较）：

import numpy as np
import sys
import matplotlib.pyplot as plt

def smooth(weights, arr):
   return np.convolve(weights/weights.sum(), arr)

data = np.loadtxt(sys.argv[1], delimiter=',', usecols=(1,), unpack=True, skiprows=1) 
##reverse order
data = data[::-1]

##Select last 50 years
data = data[-50:]
year_range = np.arange(1963, 2013)
print len(data), len(year_range)

plt.plot(year_range, data, label="Data")
plt.plot(year_range, smooth(np.hanning(22), data)[21:], 'x', label='Hanning 22')
plt.plot(year_range, smooth(np.bartlett(22), data)[21:], 'o', label='Bartlett 22')
plt.plot(year_range, smooth(np.blackman(22), data)[21:], '--', label='Blackman 22')
plt.plot(year_range, smooth(np.hamming(22), data)[21:], '^', label='Hamming 22')
plt.plot(year_range, smooth(np.kaiser(22, 14), data)[21:], ':', label='Kaiser 22')
plt.legend()
plt.show()

在下图中，我们可以看到窗口函数的结果相差不大：

使用 ARMA 模型进行预测

在上一章，第 4 章，“NumPy 的简单预测分析”中，我们学习了自回归模型。 ARMA 是这些模型的概括，它为添加了额外的组成部分-移动平均值。 ARMA 模型通常用于预测时间序列的值。 这些模型结合了自回归模型和移动平均模型。 自回归模型通过假设线性组合是由先前遇到的值组成来预测值的。 例如，我们可以考虑线性组合，它是由时间序列中的先前值和之前的值组成的。 由于我们使用的是滞后两个周期的组件，因此也称为AR(2)模型。 在我们的案例中，我们将查看预测期之前一年和两年之前的黑子数。 在 ARMA 模型中，我们尝试对无法从上一时期的数据（也称为意外成分）无法解释的残渣进行建模。 在此，再次假定为线性组合。 因此，我们将在这里尝试使用的 ARMA（ARMA(2, 1)）模型是AR(2)模型与一阶残差的线性组合的总和。 幸运的是，我们可以使用statsmodels函数进行此分析。

我们还将使用作为statsmodels分布一部分的样本黑子数据。 根据您上次安装statsmodels的时间，此数据集可能不是最新的。 无论如何，您都可以始终仅使用本章第一节中提到的数据集。 可以通过以下步骤进行预测：

1. 将数据加载到DataFramePandas 中。 我们还必须指定可用的年份范围，并使用以下代码摆脱Year列：

   df = sm.datasets.sunspots.load_pandas().data
   
   df.index = pandas.Index(sm.tsa.datetools.dates_from_range('1700', '2008'))
   del df["YEAR"]
   

2. 使用以下代码将数据拟合为ARMA(2, 1)模型：

   model = sm.tsa.ARMA(df, (2,1)).fit()
   

3. 使用以下代码进行预测：

   prediction = model.predict('1984', str(year_today), dynamic=True)
   

以下代码是带有绘图的完整代码清单：

import numpy as np
from scipy import stats
import pandas

import matplotlib.pyplot as plt
import statsmodels.api as sm
import datetime

df = sm.datasets.sunspots.load_pandas().data

df.index = pandas.Index(sm.tsa.datetools.dates_from_range('1700', '2008'))
del df["YEAR"]

model = sm.tsa.ARMA(df, (2,1)).fit()

year_today = datetime.date.today().year

##Big Brother is watching you!
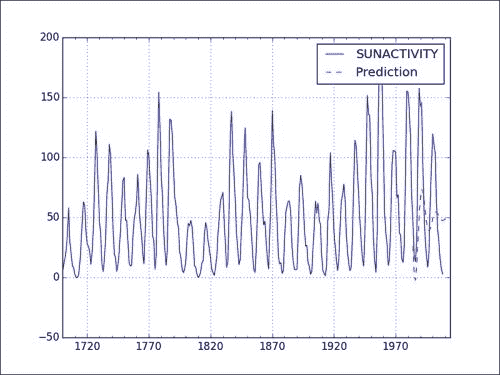
prediction = model.predict('1984', str(year_today), dynamic=True)

df.plot()
prediction.plot(style='--', label='Prediction');
plt.legend();
plt.show()

请参考以下预测和实际数据图表：

过滤信号

另一种常见的信号处理技术是过滤。 这是一个很大的话题，我们可以创建各种过滤器。 我们只会在这里创建一个非常基本的过滤器。 同样，我们将使用黑子数据作为输入。

顾名思义，iirdesign函数使我们能够构造几种类型的模拟和数字过滤器。

设计过滤器

使用scipy.signal模块的iirdesign函数设计过滤器。

注意

IIR 代表无限冲激响应； 有关更多信息，请访问这里。

我们将不涉及iirdesign函数的所有细节。 如果需要，请查看文档。 简而言之，以下是我们将设置的参数：

• 频率标准化为从 0 到 1。
• 最大损失。
• 最小衰减。
• 过滤器类型。

可以使用以下代码来设计过滤器：

b,a = scipy.signal.iirdesign(wp=0.2, ws=0.1, gstop=60, gpass=1, ftype='but ter')

注意

该过滤器的配置与 Butterworth 带通过滤器相对应。

我们可以通过scipy.signal.lfilter函数应用过滤器。 它接受上一步的值作为参数，当然也接受数据数组作为过滤参数，如以下代码所示：

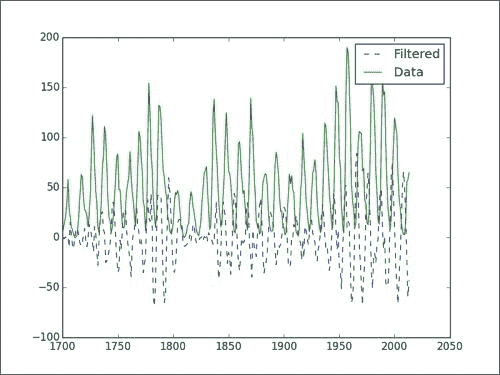
filtered = scipy.signal.lfilter(b, a, data)

如果我们绘制原始数据和过滤后的数据，则会得到以下图表：

演示协整

协整与相关性相似，但许多人认为它是定义两个时间序列的相关性的较好度量。 解释协整和相关之间差异的通常方法是以一个醉酒的人和他的狗为例。 相关性告诉您有关它们前进方向的一些信息。 协整与它们随时间的距离有关，在这种情况下，其受狗的牵引力约束。 我们将使用计算机生成的时间序列和真实数据演示协整。 可以从 Quandl 以 CSV 格式下载数据。

增强迪基·富勒（ADF）测试可用于测量时间序列的协整； 继续执行以下步骤来演示协整：

1. 定义以下函数以计算 ADF 统计量。

   def calc_adf(x, y):
       result = stat.OLS(x, y).fit()    
       return ts.adfuller(result.resid)
   

2. 生成一个sin值，并计算该值与自身的协整：

   N = 501
   t = np.linspace(-2 * np.pi, 2 * np.pi, N)
   sine = np.sin(np.sin(t))
   print "Self ADF", calc_adf(sine, sine)
   

   这应该打印以下内容：

   Self ADF (2.9830728873654705e-17, 0.95853208606005602, 0, 500, {'5%': -2.8673378563200003, '1%': -3.4434963794639999, '10%': -2.5698580359999998}, -35895.784416878145)
   
   

   您看到的第一个值是 ADF 指标本身。 第二个数字是 p 值。 如您所见，p 值很高。 然后跟踪滞后和样本量。 字典给出了此特定样本大小的 T 分布值。

3. 现在向正弦添加噪声：

   noise = np.random.normal(0, .01, N)
   print "ADF sine with noise", calc_adf(sine, sine + noise)
   

   添加噪声可获得以下结果：

   ADF sine with noise (-23.84029624339999, 0.0, 0, 500, {'5%': -2.8673378563200003, '1%': -3.4434963794639999, '10%': -2.5698580359999998}, -3147.9631889288148)
   
   

   在这里看来，我们可以根据找到的 p 值来拒绝协整。

4. 让我们生成一个更大幅度和偏移量的cos值。 再次让我们添加噪音：

   cosine = 100 * np.cos(t) + 10
   print "ADF sine vs cosine with noise", calc_adf(sine, cosine + noise)
   

   给出以下值：

   ADF sine vs cosine with noise (-4.7019725364090377, 8.3437700445205561e-05, 18, 482, {'5%': -2.8675550551408353, '1%': -3.4439899743408136, '10%': -2.5699737921179042}, -18152.922572321968)
   
   

   同样，在这里我们看到对协整的强烈反对。

5. 现在介绍可以从以下代码片段中提供的 URL 下载的真实数据：

   #http://www.quandl.com/BUNDESBANK/BBK01_WT5511-Gold-Price-USD
   gold = np.loadtxt(sys.argv[1] + '/BBK01_WT5511.csv', delimiter=',', usecols=(1,), unpack=True, skiprows=1) 
   
   #http://www.quandl.com/YAHOO/INDEX_GSPC-S-P-500-Index
   sp500 = np.loadtxt(sys.argv[1] + '/INDEX_GSPC.csv', delimiter=',', usecols=(6,), unpack=True, skiprows=1)
   

6. 在这里，我们必须确保两个时间序列对齐并且顺序正确：

   sp500 = sp500[-len(gold):]
   gold = gold[::-1]
   sp500 = sp500[::-1]
   print "Gold v S & P 500", calc_adf(gold, sp500)
   

   结果表明似乎有一些协整的证据：

   Gold v S & P 500 (-1.8835008669539355, 0.3398621844965054, 31, 11545, {'5%': -2.861790382593266, '1%': -3.4309165443532876, '10%': -2.566903273565075}, 83668.547346270294)
   
   

请参考以下代码：

import numpy as np
import statsmodels.api as stat
import statsmodels.tsa.stattools as ts
import sys

def calc_adf(x, y):
    result = stat.OLS(x, y).fit()    
    return ts.adfuller(result.resid)

N = 501
t = np.linspace(-2 * np.pi, 2 * np.pi, N)
sine = np.sin(np.sin(t))
print "Self ADF", calc_adf(sine, sine)

noise = np.random.normal(0, .01, N)
print "ADF sine with noise", calc_adf(sine, sine + noise)

cosine = 100 * np.cos(t) + 10
print "ADF sine vs cosine with noise", calc_adf(sine, cosine + noise)

##http://www.quandl.com/BUNDESBANK/BBK01_WT5511-Gold-Price-USD
gold = np.loadtxt(sys.argv[1] + '/BBK01_WT5511.csv', delimiter=',', usecols=(1,), unpack=True, skiprows=1) 

##http://www.quandl.com/YAHOO/INDEX_GSPC-S-P-500-Index
sp500 = np.loadtxt(sys.argv[1] + '/INDEX_GSPC.csv', delimiter=',', usecols=(6,), unpack=True, skiprows=1) 
sp500 = sp500[-len(gold):]
gold = gold[::-1]
sp500 = sp500[::-1]
print "Gold v S & P 500", calc_adf(gold, sp500)

总结

在本章中，我们学习了许多复杂的信号处理技术。 其中大多数被应用于黑子数据集。 我们研究了使用窗口函数和移动平均值进行的平滑。 我们还谈到了科学家用于得出黑子周期的过滤过程。 最后但并非最不重要的是，给出了协整的演示。

在下一章中，我们将专注于调试，概要分析和测试，包括断言函数和各种工具。

标签：plt,temp,手册,数组,np,NumPy,我们
From： https://www.cnblogs.com/apachecn/p/17314342.html