原文:NumPy Cookbook - Second Edition
译者:飞龙
在本章中,我们将介绍以下秘籍:
- 安装 Cython
- 构建 HelloWorld 程序
- 将 Cython 与 NumPy 结合使用
- 调用 C 函数
- 分析 Cython 代码
- 用 Cython 近似阶乘
简介
Cython 是基于 Python 的相对年轻的编程语言。 它允许编码人员将 C 的速度与 Python 的功能混合在一起。 与 Python 的区别在于我们可以选择声明静态类型。 许多编程语言(例如 C)具有静态类型,这意味着我们必须告诉 C 变量的类型,函数参数和返回值类型。 另一个区别是 C 是一种编译语言,而 Python 是一种解释语言。 根据经验,可以说 C 比 Python 更快,但灵活性更低。 通过 Cython 代码,我们可以生成 C 或 C++ 代码。 之后,我们可以将生成的代码编译为 Python 扩展模块。
在本章中,您将学习 Cython。 我们将获得一些与 NumPy 一起运行的简单 Cython 程序。 另外,我们将介绍 Cython 代码。
安装 Cython
为了使用 Cython,我们需要安装它。 Enthought Canopy,Anaconda 和 Sage 发行版包括 Cython。 有关更多信息,请参见这里,这里和这里。 我们将不在这里讨论如何安装这些发行版。 显然,我们需要一个 C 编译器来编译生成的 C 代码。 在某些操作系统(例如 Linux)上,编译器将已经存在。 在本秘籍中,我们将假定您已经安装了编译器。
操作步骤
我们可以使用以下任何一种方法来安装 Cython:
-
通过执行以下步骤从源存档中安装 Cython :
-
打开包装。
-
使用
cd命令浏览到目录。 -
运行以下命令:
$ python setup.py install
-
使用以下任一命令从 PyPI 存储库安装 Cython:
$ easy_install cython $ sudo pip install cython -
使用非官方 Windows 安装程序,在 Windows 上安装 Cython。
另见
构建 HelloWorld 程序
与编程语言的传统一样,我们将从 HelloWorld 示例开始。 与 Python 不同,我们需要编译 Cython 代码。 我们从.pyx文件开始,然后从中生成 C 代码。 可以编译此.c文件,然后将其导入 Python 程序中。
操作步骤
本节介绍如何构建 Cython HelloWorld 程序:
-
首先,编写一些非常简单的代码以显示
Hello World。 这只是普通的 Python 代码,但文件具有pyx扩展名:def say_hello(): print "Hello World!" -
创建一个名为
setup.py的文件来帮助构建 Cython 代码:from distutils.core import setup from distutils.extension import Extension from Cython.Distutils import build_ext ext_modules = [Extension("hello", ["hello.pyx"])] setup( name = 'Hello world app', cmdclass = {'build_ext': build_ext}, ext_modules = ext_modules )如您所见,我们在上一步中指定了文件,并为应用命名。
-
使用以下命令进行构建:
$ python setup.py build_ext --inplace这将生成 C 代码,将其编译为您的平台,并产生以下输出:
running build_ext cythoning hello.pyx to hello.c building 'hello' extension creating build现在,我们可以使用以下语句导入模块:
from hello import say_hello
工作原理
在此秘籍中,我们创建了一个传统的 HelloWorld 示例。 Cython 是一种编译语言,因此我们需要编译代码。 我们编写了一个包含Hello World代码的.pyx文件和一个用于生成和构建 C 代码的setup.py文件。
另见
将 Cython 与 NumPy 结合使用
我们可以集成 Cython 和 NumPy 代码,就像可以集成 Cython 和 Python 代码一样。 让我们来看一个示例,该示例分析股票的上涨天数(股票收盘价高于前一日的天数)的比率。 我们将应用二项式比值置信度的公式。 您可以参考这里了解更多信息。 以下公式说明该比率的重要性:
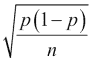
式中,p是概率,n是观察数。
操作步骤
本节通过以下步骤介绍如何将 Cython 与 NumPy 结合使用:
-
编写一个
.pyx文件,其中包含一个函数,该函数可计算上升天数的比率和相关的置信度。 首先,此函数计算价格之间的差异。 然后,它计算出正差的数量,从而得出上升天数的比率。 最后,在引言中的维基百科页面上应用置信度公式:import numpy as np def pos_confidence(numbers): diffs = np.diff(numbers) n = float(len(diffs)) p = len(diffs[diffs > 0])/n confidence = np.sqrt(p * (1 - p)/ n) return (p, confidence) -
使用上一个示例中的
setup.py文件作为模板。 更改明显的内容,例如.pyx文件的名称:from distutils.core import setup from distutils.extension import Extension from Cython.Distutils import build_ext ext_modules = [Extension("binomial_proportion", ["binomial_proportion.pyx"])] setup( name = 'Binomial proportion app', cmdclass = {'build_ext': build_ext}, ext_modules = ext_modules )我们现在可以建立; 有关更多详细信息,请参见前面的秘籍。
-
构建后,通过导入使用上一步中的 Cython 模块。 我们将编写一个 Python 程序,使用
matplotlib下载股价数据。 然后我们将confidence()函数应用于收盘价:from matplotlib.finance import quotes_historical_yahoo from datetime import date import numpy import sys from binomial_proportion import pos_confidence #1\. Get close prices. today = date.today() start = (today.year - 1, today.month, today.day) quotes = quotes_historical_yahoo(sys.argv[1], start, today) close = numpy.array([q[4] for q in quotes]) print pos_confidence(close)AAPL程序的输出如下:(0.56746031746031744, 0.031209043355655924)
工作原理
我们计算了APL股价上涨的可能性和相应的置信度。 我们通过创建 Cython 模块,将 NumPy 代码放入.pyx文件中,并按照上一教程中的步骤进行构建。 最后,我们导入并使用了 Cython 模块。
另见
调用 C 函数
我们可以从 Cython 调用 C 函数。 在此示例中,我们调用 C log()函数。 此函数仅适用于单个数字。 请记住,NumPy log()函数也可以与数组一起使用。 我们将计算股票价格的所谓对数回报。
操作步骤
我们首先编写一些 Cython 代码:
-
首先,从
libc命名空间导入 C 的log()函数。 然后,将此函数应用于for循环中的数字。 最后,使用 NumPydiff()函数在第二步中获取对数值之间的一阶差:from libc.math cimport log import numpy as np def logrets(numbers): logs = [log(x) for x in numbers] return np.diff(logs)先前的秘籍中已经介绍了架构。 我们只需要更改
setup.py文件中的某些值。 -
再次使用 matplotlib 下载股价数据。 应用您刚刚在价格上创建的 Cython
logrets()函数并绘制结果:from matplotlib.finance import quotes_historical_yahoo from datetime import date import numpy as np from log_returns import logrets import matplotlib.pyplot as plt today = date.today() start = (today.year - 1, today.month, today.day) quotes = quotes_historical_yahoo('AAPL', start, today) close = np.array([q[4] for q in quotes]) plt.plot(logrets(close)) plt.title('Logreturns of AAPL for the previous year') plt.xlabel('Days') plt.ylabel('Log returns') plt.grid() plt.show()的
AAPL对数回报结果图类似于以下屏幕截图所示:
工作原理
我们从 Cython 代码中调用了 C log()函数。 该函数与 NumPy 函数一起用于计算股票的对数收益。 这样,我们可以创建自己的包含便利函数的专用 API。 令人高兴的是,我们的代码应该或多或少地像 Python 代码一样,以与 C 代码差不多的速度执行。
另见
分析 Cython 代码
我们将使用以下公式对 Cython 和 NumPy 代码进行剖析,这些代码试图近似于欧拉常数:
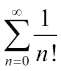
操作步骤
本节演示如何通过以下步骤来分析 Cython 代码:
-
对于
e的 NumPy 近似值,请按照下列步骤操作:-
首先,我们将创建一个
1到n的数组(在我们的示例中n是40)。 -
然后,我们将计算该数组的累积乘积,该乘积恰好是阶乘。 在那之后,我们采取阶乘的倒数。 最后,我们从维基百科页面应用公式。 最后,我们放入标准配置代码,为我们提供以下程序:
from __future__ import print_function import numpy as np import cProfile import pstats def approx_e(n=40, display=False): # array of [1, 2, ... n-1] arr = np.arange(1, n) # calculate the factorials and convert to floats arr = arr.cumprod().astype(float) # reciprocal 1/n arr = np.reciprocal(arr) if display: print(1 + arr.sum()) # Repeat multiple times because NumPy is so fast def run(repeat=2000): for i in range(repeat): approx_e() cProfile.runctx("run()", globals(), locals(), "Profile.prof") s = pstats.Stats("Profile.prof") s.strip_dirs().sort_stats("time").print_stats() approx_e(display=True)
以下代码段显示了
e的近似值的分析输出和结果。 有关概要分析输出的更多信息,请参见第 7 章,“分析和调试”。8004 function calls in 0.016 seconds Ordered by: internal time ncalls tottime percall cumtime percall filename:lineno(function) 2000 0.007 0.000 0.015 0.000 numpy_approxe.py:6(approx_e) 2000 0.004 0.000 0.004 0.000 {method 'cumprod' of 'numpy.ndarray' objects} 2000 0.002 0.000 0.002 0.000 {numpy.core.multiarray.arange} 2000 0.002 0.000 0.002 0.000 {method 'astype' of 'numpy.ndarray' objects} 1 0.001 0.001 0.016 0.016 numpy_approxe.py:20(run) 1 0.000 0.000 0.000 0.000 {range} 1 0.000 0.000 0.016 0.016 <string>:1(<module>) 1 0.000 0.000 0.000 0.000 {method 'disable' of '_lsprof.Profiler' objects} 2.71828182846 -
-
Cython 代码使用与上一步所示相同的算法,但是实现方式不同。 便利函数较少,实际上我们现在需要一个
for循环。 另外,我们需要为某些变量指定类型。.pyx文件的代码如下所示:def approx_e(int n=40, display=False): cdef double sum = 0. cdef double factorial = 1. cdef int k for k in xrange(1,n+1): factorial *= k sum += 1/factorial if display: print(1 + sum)以下 Python 程序导入 Cython 模块并进行一些分析:
import pstats import cProfile import pyximport pyximport.install() import approxe # Repeat multiple times because Cython is so fast def run(repeat=2000): for i in range(repeat): approxe.approx_e() cProfile.runctx("run()", globals(), locals(), "Profile.prof") s = pstats.Stats("Profile.prof") s.strip_dirs().sort_stats("time").print_stats() approxe.approx_e(display=True)这是 Cython 代码的分析输出:
2004 function calls in 0.001 seconds Ordered by: internal time ncalls tottime percall cumtime percall filename:lineno(function) 2000 0.001 0.000 0.001 0.000 {approxe.approx_e} 1 0.000 0.000 0.001 0.001 cython_profile.py:9(run) 1 0.000 0.000 0.000 0.000 {range} 1 0.000 0.000 0.001 0.001 <string>:1(<module>) 1 0.000 0.000 0.000 0.000 {method 'disable' of '_lsprof.Profiler' objects} 2.71828182846
工作原理
我们分析了 NumPy 和 Cython 代码。 NumPy 已针对速度进行了优化,因此 NumPy 和 Cython 程序都是高性能程序,我们对此不会感到惊讶。 但是,当比较 2,000 次近似代码的总时间时,我们意识到 NumPy 需要 0.016 秒,而 Cython 仅需要 0.001 秒。 显然,实际时间取决于硬件,操作系统和其他因素,例如计算机上运行的其他进程。 同样,提速取决于代码类型,但我希望您同意,根据经验,Cython 代码会更快。
另见
Cython 的近似阶乘
最后一个示例是 Cython 的近似阶乘。 我们将使用两种近似方法。 首先,我们将应用斯特林近似方法。 斯特林近似的公式如下:

其次,我们将使用 Ramanujan 的近似值,并使用以下公式:
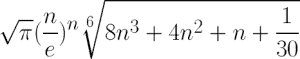
操作步骤
本节介绍如何使用 Cython 近似阶乘。 您可能还记得,在本秘籍中,我们使用在 Cython 中可选的类型。 从理论上讲,声明静态类型应加快速度。 静态类型化提供了一些有趣的挑战,这些挑战在编写 Python 代码时可能不会遇到,但请不要担心。 我们将尝试使其简单:
-
除了将函数参数和一个局部变量声明为
ndarray数组外,我们将编写的 Cython 代码类似于常规的 Python 代码。 为了使静态类型起作用,我们需要cimportNumPy。 另外,我们必须使用cdef关键字声明局部变量的类型:import numpy cimport numpy def ramanujan_factorial(numpy.ndarray n): sqrt_pi = numpy.sqrt(numpy.pi, dtype=numpy.float64) cdef numpy.ndarray root = (8 * n + 4) * n + 1 root = root * n + 1/30. root = root ** (1/6.) return sqrt_pi * calc_eton(n) * root def stirling_factorial(numpy.ndarray n): return numpy.sqrt(2 * numpy.pi * n) * calc_eton(n) def calc_eton(numpy.ndarray n): return (n/numpy.e) ** n -
如先前的教程所示,构建需要我们创建一个
setup.py文件,但是现在我们通过调用get_include()函数来包含与 NumPy 相关的目录。 通过此修订,setup.py文件具有以下内容:from distutils.core import setup from distutils.extension import Extension from Cython.Distutils import build_ext import numpy ext_modules = [Extension("factorial", ["factorial.pyx"], include_dirs = [numpy.get_include()])] setup( name = 'Factorial app', cmdclass = {'build_ext': build_ext}, ext_modules = ext_modules ) -
绘制两种近似方法的相对误差。 像我们在整本书中所做的那样,将使用 NumPy
cumprod()函数计算相对于阶乘值的误差:from factorial import ramanujan_factorial from factorial import stirling_factorial import numpy as np import matplotlib.pyplot as plt N = 50 numbers = np.arange(1, N) factorials = np.cumprod(numbers, dtype=float) def error(approximations): return (factorials - approximations)/factorials plt.plot(error(ramanujan_factorial(numbers)), 'b-', label='Ramanujan') plt.plot(error(stirling_factorial(numbers)), 'ro', label='Stirling') plt.title('Factorial approximation relative errors') plt.xlabel('n') plt.ylabel('Relative error') plt.grid() plt.legend(loc='best') plt.show()下图显示了 Ramanujan 近似值(点)和 Stirling 近似值(线)的相对误差:
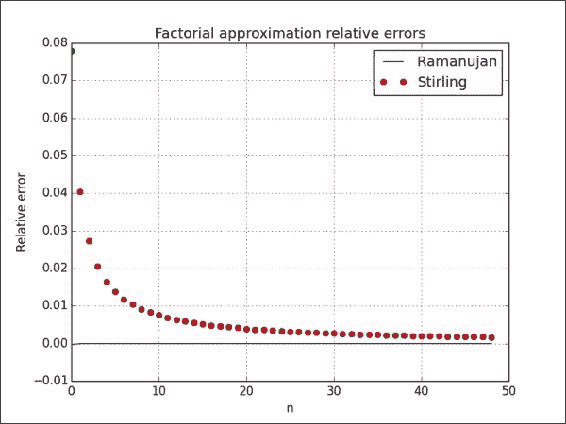
工作原理
在此示例中,我们看到了 Cython 静态类型的演示。 该秘籍的主要成分如下:
cimport,它导入 C 声明- 包含具有
get_include()函数的目录 cdef关键字,用于定义局部变量的类型