标签：11 12 meanp selection print range plt np NumPy

原文：NumPy Cookbook - Second Edition

协议：CC BY-NC-SA 4.0

译者：飞龙

十一、最新最强的 NumPy

在本章中，我们涵盖以下秘籍：

用at()方法用花式索引代替 ufuncs
通过使用partition()函数选择快速中位数进行部分排序
使用nanmean()，nanvar()和nanstd()函数跳过 NaN
使用full()和full_like()函数创建值初始化的数组
numpy.random.choice()随机抽样
使用datetime64类型和相关的 API

简介

自《NumPy 秘籍》第一版以来，NumPy 团队引入了新功能；我将在本章中对其进行描述。您可能不太可能阅读本书的第一版，而现在正在阅读第二版。我在 2012 年撰写了第一版，并使用了当时可用的功能。 NumPy 具有许多功能，因此您不能期望涵盖所有功能，但是我在本章中介绍的功能相对重要。

使用`at()`方法为 ufuncs 建立花式索引

at()方法已添加到 NumPy 1.8 的 NumPy 通用函数类中。此方法允许就地进行花式索引。花式索引是不涉及整数或切片的索引，这是正常的索引。 “就地”是指将更改输入数组的数据。

at()方法的签名为ufunc.at(a, indices[, b])。索引数组对应于要操作的元素。我们仅必须为具有两个操作数的通用函数指定b数组。

操作步骤

以下步骤演示了at()方法的工作方式：

创建一个具有种子44的7个从-4到4的随机整数的数组。

np.random.seed(44)
a = np.random.random_integers(-4, 4, 7)
print(a)

该数组如下所示：

[ 0 -1 -3 -1 -4  0 -1]

将sign通用函数的at()方法应用于第三和第五个数组元素：
```
np.sign.at(a, [2, 4])
print(a)
```
我们得到以下更改后的数组：
```
[ 0 -1 -1 -1 -1  0 -1]
```

另见

NumPy 通用函数文档

使用`partition()`函数通过快速中位数的选择进行部分排序

partition()子例程进行部分排序。这应该比正常的分类工作少。

注意

有关更多信息，请参见这里。有用的情况是选择组中的前五项（或其他一些数字）。部分排序不能在顶部元素集中保留正确的顺序。

子例程的第一个参数是要排序的输入数组。第二个参数是整数或与数组元素的索引相对应的整数列表。 partition()子例程正确地对那些索引处的项目进行排序。一个指定的索引给出两个分区。多个索自举致两个以上的分区。该算法保证分区中小于正确排序项目的项目位于该项目之前。否则，它们将放在该项目的后面。

操作步骤

让我们举例说明此解释：

创建一个具有随机数的数组以进行排序：

np.random.seed(20)
a = np.random.random_integers(0, 7, 9)
print(a)

该数组具有以下元素：

[3 2 7 7 4 2 1 4 3]

通过将数组划分为两个大致相等的部分，对数组进行部分排序：
```
print(np.partition(a, 4))
```
我们得到以下结果：
```
[2 3 1 2 3 7 7 4 4]
```

工作原理

我们对 9 个元素的数组进行了部分排序。该函数保证索引4,的中间只有一个元素在正确的位置。这对应于尝试选择数组的前五项而不关心前五组中的顺序。由于正确排序的项目位于中间，因此这也将返回数组的中位数。

另见

相关 NumPy 文档

使用`nanmean()`，`nanvar()`和`nanstd()`函数跳过 NaN

试图估计一组数据的算术平均值，方差和标准差是很常见的。

一种简单但有效的方法称为 Jackknife 重采样。 Jackknife 重采样的想法是通过每次都遗漏一个值来从原始数据创建数据集。本质上，我们试图估计如果至少一个值不正确会发生什么。对于每个新数据集，我们都会重新计算我们感兴趣的统计估计量。这有助于我们了解估计量的变化方式。

操作步骤

我们将折刀重采样应用于随机数据。通过将其设置为 NaN（非数字），我们将跳过每个数组元素一次。然后，可以使用nanmean()，nanvar()和nanstd()计算算术平均值，方差和标准差：

首先为估算值初始化一个30 x 3的数组，如下所示：
```
estimates = np.zeros((len(a), 3))
```
遍历数组并通过在循环的每次迭代中将一个值设置为 NaN 来创建新的数据集。对于每个新数据集，计算估计值：
```
for i in xrange(len(a)):
   b = a.copy()
   b[i] = np.nan
   estimates[i,] = [np.nanmean(b), np.nanvar(b), np.nanstd(b)]
```

打印每个估计量的方差：

print("Estimator variance", estimates.var(axis=0))

屏幕上显示以下输出：

Estimator variance [ 0.00079905  0.00090129  0.00034604]

工作原理

我们用折刀重采样估计了数据集的算术平均值，方差和标准差的方差。这表明算术平均值，方差和标准差有多少变化。该秘籍的代码在本书的代码包的jackknife.py 文件中：

from __future__ import print_function
import numpy as np

np.random.seed(46)
a = np.random.randn(30)
estimates = np.zeros((len(a), 3))

for i in xrange(len(a)):
   b = a.copy()
   b[i] = np.nan

   estimates[i,] = [np.nanmean(b), np.nanvar(b), np.nanstd(b)]

print("Estimator variance", estimates.var(axis=0))

另见

使用`full()`和`full_like()`函数创建初始化值的数组

full()和full_like()函数是 NumPy 的新增函数，旨在促进初始化。这是文档中关于它们的内容：

>>> help(np.full)
Return a new array of given shape and type, filled with `fill_value`.
>>> help(np.full_like)
Return a full array with the same shape and type as a given array.

操作步骤

让我们看一下full()和full_like()函数：

用full()创建一个1x2数组，并填充幸运数字7：
```
print(np.full((1, 2), 7))
```
因此，我们得到以下数组：
```
array([[ 7.,  7.]])
```
数组元素是浮点数。
指定整数数据类型，如下所示：
```
print(np.full((1, 2), 7, dtype=np.int))
```
输出相应地更改：
```
array([[7, 7]])
```
full_like()函数检查数组的元数据，并将其重新用于新数组。例如，使用linspace()创建一个数组，并将其用作full_like()函数的模板：
```
a = np.linspace(0, 1, 5)
print(a)
array([ 0\.  ,  0.25,  0.5 ,  0.75,  1\.  ])
print(np.full_like(a, 7))
array([ 7.,  7.,  7.,  7.,  7.])
```
同样，我们用幸运数字7填充数组。要将数据类型修改为整数，请在以下行中使用：
```
print(np.full_like(a, 7, dtype=np.int))
array([7, 7, 7, 7, 7])
```

工作原理

我们用full()和full_like()产生了数组。 full()函数用数字7填充数组。 full_like()函数重新使用了数组的元数据来创建新的数组。这两个函数都可以指定数组的数据类型。

使用`numpy.random.choice()`进行随机采样

自举的过程类似于粗加工。基本的自举方法包括以下步骤：

从大小为 N 的原始数据生成样本。将原始数据样本可视化为一碗数字。我们通过从碗中随机抽取数字来创建新样本。取一个数字后，我们将其放回碗中。
对于每个生成的样本，我们计算感兴趣的统计估计量（例如，算术平均值）。

操作步骤

我们将应用numpy.random.choice()进行自举：

按照二项式分布生成数据样本，该数据样本模拟五次抛掷公平硬币：
```
N = 400
np.random.seed(28)
data = np.random.binomial(5, .5, size=N)
```

生成 30 个样本并计算其平均值（更多样本将得到更好的结果）：

bootstrapped = np.random.choice(data, size=(N, 30))
means = bootstrapped.mean(axis=0)

使用 matplotlib 箱形图可视化算术平均值分布：

plt.title('Bootstrapping demo')
plt.grid()
plt.boxplot(means)
plt.plot(3 * [data.mean()], lw=3, label='Original mean')
plt.legend(loc='best')
plt.show()

有关最终结果，请参考以下带注释的图：

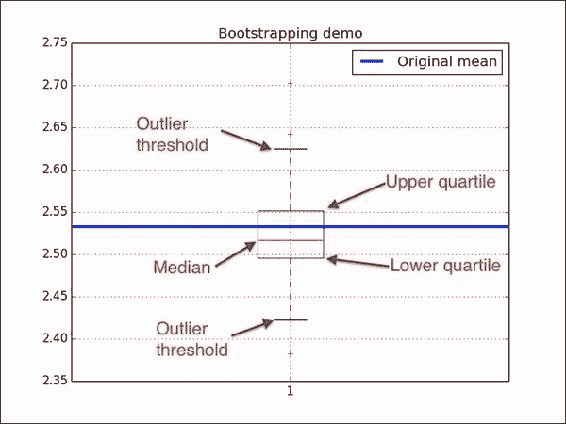
How to do it...

工作原理

我们模拟了一个实验，该实验涉及掷出五次公平硬币。我们通过创建样本并计算相应的方法来自举数据。然后，我们使用numpy.random.choice()进行自举。我们用matplotlib箱形图直观地表示了均值。如果您不熟悉箱形图，图中的注释将对您有所帮助。箱形图中的以下元素很重要：

中位数由框中的一条线表示。
上下四分位数显示为框的边界。
胡须指示异常值的边界。默认情况下，这些值从框的边界设置为1.5 * (Q3 - Q1)，也称为四分位间距。

另见

使用`datetime64`类型和相关的 API

datetime64类型表示相应的日期和时间。您需要 NumPy 1.7.0 或更高版本才能使用此数据类型。

操作步骤

要熟悉datetime64，请按照下列步骤操作：

从字符串创建一个datetime64，如下所示：
```
print(np.datetime64('2015-05-21'))
```
前一行输出以下输出：
```
numpy.datetime64('2015-05-21')
```
我们使用YYYY-MM-DD格式在 2015 年 5 月 21 日创建了datetime64类型，其中Y对应于年份，M对应于月份，D对应于每月的一天。 NumPy 符合 ISO 8601 标准 -- 一种表示日期和时间的国际标准。

ISO 8601 还定义了YYYY-MM-DD，YYYY-MM和YYYYMMDD格式。自己检查这些，如下所示：

print(np.datetime64('20150521'))
print(np.datetime64('2015-05'))

该代码显示以下行：

numpy.datetime64('20150521')
numpy.datetime64('2015-05')

默认情况下，ISO 8601 使用本地时区。可以使用T[hh:mm:ss]格式指定时间。例如，我们可以定义 1578 年 1 月 1 日和晚上 9:18。如下：
```
local = np.datetime64('1578-01-01T21:18')
print(local)
```
以下行显示了结果：
```
numpy.datetime64('1578-01-01T21:18Z')
```
格式为-[hh:mm]的字符串定义相对于 UTC 时区的偏移量。我们可以使用 8 个小时的偏移量创建一个datetime64类型，如下所示：
```
with_offset = np.datetime64('1578-01-01T21:18-0800')
print(with_offset)
```
然后，我们在屏幕上看到以下行：
```
numpy.datetime64('1578-01-02T05:18Z')
```
最后的Z代表 Zulu 时间，有时也称为 UTC。
相互减去两个datetime64对象：
```
print(local - with_offset)
```
结果显示如下：
```
numpy.timedelta64(-480,'m')
```
减法创建一个timedelta64 NumPy 对象，在这种情况下，它表示 480 分钟的增量。

工作原理

您了解了datetime64 NumPy 类型。这种数据类型使我们可以轻松地操纵日期和时间。它的功能包括简单的算术运算和使用常规 NumPy 函数创建数组。请参考本书代码包中的datetime_demo.py文件：

import numpy as np

print(np.datetime64('2015-05-21'))
#numpy.datetime64('2015-05-21')

print(np.datetime64('20150521'))
print(np.datetime64('2015-05'))
#numpy.datetime64('20150521')
#numpy.datetime64('2015-05')

local = np.datetime64('1578-01-01T21:18')
print(local)
#numpy.datetime64('1578-01-01T21:18Z')

with_offset = np.datetime64('1578-01-01T21:18-0800')
print(with_offset)
#numpy.datetime64('1578-01-02T05:18Z')

print(local - with_offset)

另见

十二、使用 NumPy 进行探索性和预测性数据分析

在本章中，我们涵盖以下秘籍：

探索气压
探索日常气压范围
研究年度气压平均值
分析最大可见度
用自回归模型预测气压
使用移动平均模型预测气压
研究年内平均气压
研究气压的极值

简介

数据分析是 NumPy 最重要的用例之一。根据我们的目标，我们可以区分数据分析的许多阶段和类型。在本章中，我们将讨论探索性和预测性数据分析。探索性数据分析可探查数据的线索。在此阶段，我们可能不熟悉数据集。预测分析试图使用模型来预测有关数据的某些信息。

数据来自荷兰气象局 KNMI。特别是 KNMI 总部位于 De Bilt 的气象站。在这些秘籍中，我们将检查气压和最大可见度。

我修改了文本数据并将其从 KNMI 转换为 NumPy 特定的.npy格式，并保存为40996 x 5数组。该数组包含五个变量的每日值：

YYYYMMDD格式的日期
每日平均气压
每日最高气压
每日最低气压
每日最大可见度

探索气压

在此秘籍中，我们将查看由 24 小时值计算出的每日平均海平面气压（0.1 hPa）。这包括打印描述性统计数据和可视化概率分布。在自然界中，我们经常处理正态分布，因此使用第 10 章，“使用 Scikits 进行正态性检验”会派上用场。

完整的代码在本书代码包的exploring.py文件中：

from __future__ import print_function
import numpy as np
import matplotlib.pyplot as plt
from statsmodels.stats.adnorm import normal_ad

data = np.load('cbk12.npy')

# Multiply to get hPa values
meanp = .1 * data[:,1]

# Filter out 0 values
meanp = meanp[ meanp > 0]

# Get descriptive statistics
print("Max", meanp.max())
print("Min", meanp.min())
mean = meanp.mean()
print("Mean", mean)
print("Median", np.median(meanp))
std = meanp.std()
print("Std dev", std)

# Check for normality
print("Normality", normal_ad(meanp))

#histogram with Gaussian PDF
plt.subplot(211)
plt.title('Histogram of average atmospheric pressure')
_, bins, _ = plt.hist(meanp, np.sqrt(len(meanp)), normed=True)
plt.plot(bins, 1/(std * np.sqrt(2 * np.pi)) * np.exp(- (bins - mean)**2/(2 * std**2)), 'r-', label="Gaussian PDF")
plt.grid()
plt.legend(loc='best')
plt.xlabel('Average atmospheric pressure (hPa)')
plt.ylabel('Frequency')

# boxplot
plt.subplot(212)
plt.boxplot(meanp)
plt.title('Boxplot of average atmospheric pressure')
plt.ylabel('Average atmospheric pressure (hPa)')
plt.grid()

# Improves spacing of subplots
plt.tight_layout()
plt.show()

准备

如果尚未安装，请安装statsmodels以进行正态性测试（请参阅第 10 章，“Scikits 的乐趣”的“安装 scikits-statsmodels”秘籍）。

操作步骤

请按照以下步骤探索每日气压：

使用load()函数加载数据：
```
data = np.load('cbk12.npy')
```
通常，数据需要进行处理和清理。在这种情况下，将这些值相乘以获得hPa中的值，然后删除与缺失值相对应的0值：
```
# Multiply to get hPa values
meanp = .1 * data[:,1]

# Filter out 0 values
meanp = meanp[ meanp > 0]
```

获取描述性统计信息，包括最大值，最小值，算术平均值，中位数和标准差：

print("Max", meanp.max())
print("Min", meanp.min())
mean = meanp.mean()
print("Mean", mean)
print("Median", np.median(meanp))
std = meanp.std()
print("Std dev", std)

您应该看到以下值：

Max 1048.3
Min 962.1
Mean 1015.14058231
Median 1015.8
Std dev 9.85889134337

如下应用第 10 章“Scikits 的乐趣”的正态性检验：
```
print("Normality", normal_ad(meanp))
```
屏幕上显示以下值：
```
Normality (72.685781095773564, 0.0)
```
用直方图和箱形图可视化值的分布也很好。最终结果请参考以下图表：

另见

“使用 Statsmodels”秘籍执行正态性测试，该秘籍来自第 10 章，“Scikits 的乐趣”
有关箱形图的说明，请参见第 11 章“最新最强的 NumPy”
load()函数的文档

探索日常气压范围

每日气压范围是每日最高点和最低点之差。使用实际数据，有时我们会缺少一些值。在这里，我们可能会缺少给定一天的高压和/或低压值。可以通过智能算法来填补这些空白。但是，让我们保持简单，而忽略它们。在计算了范围之后，我们将进行与前面的秘籍类似的分析，但是我们将使用可以处理NaN值的函数。另外，我们将研究月份和范围之间的关系。

本书代码包中的day_range.py文件位于对应的代码中：

from __future__ import print_function
import numpy as np
import matplotlib.pyplot as plt
import calendar as cal

data = np.load('cbk12.npy')

# Multiply to get hPa values
highs = .1 * data[:,2]
lows = .1 * data[:,3]

# Filter out 0 values
highs[highs == 0] = np.nan
lows[lows == 0] = np.nan

# Calculate range and stats
ranges = highs - lows
print("Minimum daily range", np.nanmin(ranges))
print("Maximum daily range", np.nanmax(ranges))

print("Average daily range", np.nanmean(ranges))
print("Standard deviation", np.nanstd(ranges))

# Get months
dates = data[:,0]
months = (dates % 10000)/100
months = months[~np.isnan(ranges)]

monthly = []
month_range = np.arange(1, 13)

for month in month_range:
   indices = np.where(month == months)
   monthly.append(np.nanmean(ranges[indices]))

plt.bar(month_range, monthly)
plt.title('Monthly average of daily pressure ranges')
plt.xticks(month_range, cal.month_abbr[1:13])
plt.ylabel('Monthly Average (hPa)')
plt.grid()
plt.show()

操作步骤

此秘籍的第一步与先前的秘籍几乎相同，因此我们将跳过它们。继续分析每日气压范围：

我们可以将缺失值保留为当前的0值。但是，通常将它们设置为NaN较为安全，以避免造成混淆。将缺失值设置为NaN，如下所示：
```
highs[highs == 0] = np.nan
lows[lows == 0] = np.nan
```

使用nanmin()，nanmax()，nanmean()和nanstd()函数计算范围，最小值，最大值，均值和标准差：

ranges = highs - lows
print("Minimum daily range", np.nanmin(ranges))
print("Maximum daily range", np.nanmax(ranges))

print("Average daily range", np.nanmean(ranges))
print("Standard deviation", np.nanstd(ranges))

结果出现在屏幕上：

Minimum daily range 0.4
Maximum daily range 41.7
Average daily range 6.11945360571
Standard deviation 4.42162136692

如前所述，日期以YYYYMMDD格式给出。有了一点算术，我们就可以轻松地得到几个月。此外，我们忽略与NaN范围值相对应的月份值：
```
dates = data[:,0]
months = (dates % 10000)/100
months = months[~np.isnan(ranges)]
```
按月对范围进行平均，如下所示：
```
monthly = []
month_range = np.arange(1, 13)

for month in month_range:
   indices = np.where(month == months)
   monthly.append(np.nanmean(ranges[indices]))
```
在最后一步中，我们绘制了matplotlib条形图，显示了每日气压范围的每月平均值。最终结果请参考以下图表：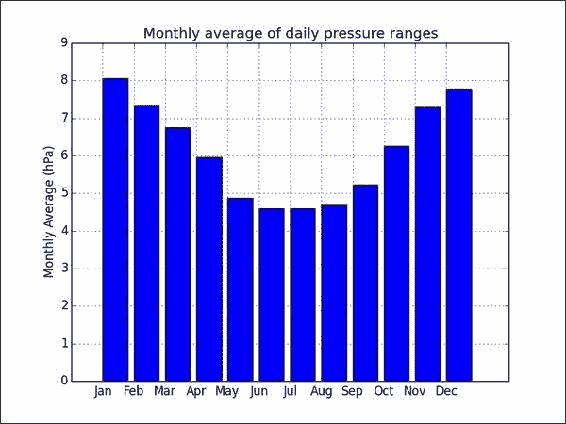

工作原理

我们分析了气压的每日范围。此外，我们可视化了每日范围的每月平均值。似乎有一种模式导致夏季的每日气压范围变小。当然，需要做更多的工作来确定。

另见

“探索气压”秘籍

研究年度气压平均值

您可能听说过，全球变暖表明温度逐年稳定上升。由于气压是另一个热力学变量，因此我们可以预期气压也会跟随趋势。该秘籍的完整代码在本书代码包的annual.py文件中：

import numpy as np
import matplotlib.pyplot as plt

data = np.load('cbk12.npy')

# Multiply to get hPa values
avgs = .1 * data[:,1]
highs = .1 * data[:,2]
lows = .1 * data[:,3]

# Filter out 0 values
avgs = np.ma.array(avgs, mask = avgs == 0)
lows = np.ma.array(lows, mask = lows == 0)
highs = np.ma.array(highs, mask = highs == 0)

# Get years
years = data[:,0]/10000

# Initialize annual stats arrays
y_range = np.arange(1901, 2014)
nyears = len(y_range)
y_avgs = np.zeros(nyears)
y_highs = np.zeros(nyears)
y_lows = np.zeros(nyears)

# Compute stats
for year in y_range:
   indices = np.where(year == years)
   y_avgs[year - 1901] = np.mean(avgs[indices])
   y_highs[year - 1901] = np.max(highs[indices])
   y_lows[year - 1901] = np.min(lows[indices])

plt.title('Annual atmospheric pressure for De Bilt(NL)')
plt.ticklabel_format(useOffset=900, axis='y')

plt.plot(y_range, y_avgs, label='Averages')

# Plot ignoring NaNs
h_mask = np.isfinite(y_highs)
plt.plot(y_range[h_mask], y_highs[h_mask], '^', label='Highs')

l_mask = np.isfinite(y_lows)
plt.plot(y_range[l_mask], y_lows[l_mask], 'v', label='Lows')

plt.xlabel('Year')
plt.ylabel('Atmospheric pressure (hPa)')
plt.grid()
plt.legend(loc='best')
plt.show()

操作步骤

要检查趋势，让我们按以下步骤绘制平均，最大和最小年度气气压：

初始化年度统计数据数组：

y_range = np.arange(1901, 2014)
nyears = len(y_range)
y_avgs = np.zeros(nyears)
y_highs = np.zeros(nyears)
y_lows = np.zeros(nyears)

计算年度统计数据：

for year in y_range:
   indices = np.where(year == years)
   y_avgs[year - 1901] = np.mean(avgs[indices])
   y_highs[year - 1901] = np.max(highs[indices])
   y_lows[year - 1901] = np.min(lows[indices])

绘制，忽略NaN值，如下所示：

h_mask = np.isfinite(y_highs)
plt.plot(y_range[h_mask], y_highs[h_mask], '^', label='Highs')

l_mask = np.isfinite(y_lows)
plt.plot(y_range[l_mask], y_lows[l_mask], 'v', label='Lows')

最终结果请参考以下图表：

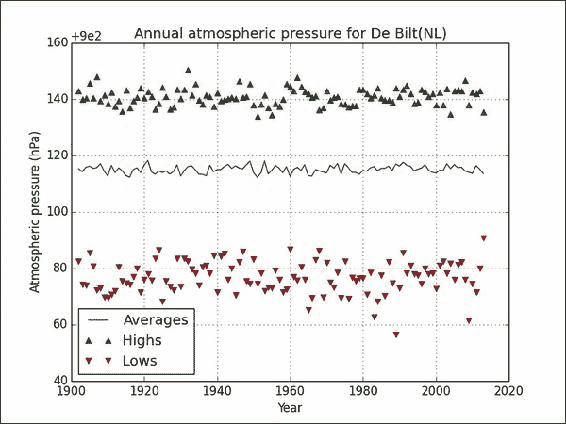
How to do it...

工作原理

年平均气压似乎持平或有所波动，但没有任何趋势。我们使用isfinite()函数忽略了最终图中的NaN值。此函数检查无限值和NaN值。

另见

“探索气压”秘籍
isfinite()函数的文档

分析最大可见度

如果到目前为止，您在本章的所有秘籍中均未使用，则可能需要突破气压。因此，让我们来看看能见度。数据文件具有一列，以提供最大的可视性，KNMI 描述如下：

Maximum visibility; 0: <100 m, 1:100-200 m, 2:200-300 m,..., 49:4900-5000 m, 50:5-6 km, 56:6-7 km, 57:7-8 km,..., 79:29-30 km, 80:30-35 km, 81:35-40 km,..., 89: >70 km)

这里的能见度是一个离散变量，因此取平均值可能没有意义。此外，似乎我们几乎每天都有 1901 年到 1950 年之间的0值。我不相信 De Bilt 在那个时期会更加迷雾重重。出于本秘籍的目的，我们将雾定义为 1 至 2km 之间的能见度，这对应于数据文件中的10和20值。让我们还将雾度定义为 2 至 5 公里之间的能见度。这又对应于我们数据文件中的20和50。

空气污染会降低能见度，尤其是在晴天。我们可以将晴天定义为能见度高于 30km 的晴天，或数据文件中79的值。理想情况下，我们应该使用空气污染数据，但不幸的是，我们没有这些数据。据我所知，这个特殊气象站周围的空气污染水平不是很高。知道每年的晴天数很有趣。分析的代码在本书的代码包的visibility.py文件中：

import numpy as np
import matplotlib.pyplot as plt

data = np.load('cbk12.npy')

# Get minimum visibility
visibility = data[:,4]

# doy
doy = data[:,0] % 10000

doy_range = np.unique(doy)

# Initialize arrays
ndoy = len(doy_range)
mist = np.zeros(ndoy)
haze = np.zeros(ndoy)

# Compute frequencies
for i, d in enumerate(doy_range):
   indices = np.where(d == doy)
   selection = visibility[indices]

   mist_truth = (10 < selection) & (selection < 20)
   mist[i] = len(selection[mist_truth])/(1\. * len(selection))

   haze_truth = (20 < selection) & (selection < 50)
   haze[i] = len(selection[haze_truth])/(1\. * len(selection))

# Get years
years = data[:,0]/10000

# Initialize annual stats arrays
y_range = np.arange(1901, 2014)
nyears = len(y_range)
y_counts = np.zeros(nyears)

# Get annual counts
for year in y_range:
   indices = np.where(year == years)
   selection = visibility[indices]
   y_counts[year - 1901] = len(selection[selection > 79])

plt.subplot(211)
plt.plot(np.arange(1, 367), mist, color='.25', label='mist')
plt.plot(np.arange(1, 367), haze, color='0.75', lw=2, label='haze')
plt.title('Probability of mist and haze')
plt.xlabel('Day of the year')
plt.ylabel('Probability')
plt.grid()
plt.legend(loc='best')

plt.subplot(212)
plt.plot(y_range, y_counts)
plt.xlabel('Year')
plt.ylabel('Number of clear days')
plt.title('Annual counts of clear days')
plt.grid()
plt.tight_layout()
plt.show()

操作步骤

请按照以下步骤来绘制晴天的年度计数，即一年中的某一天（1-366）对霾和薄雾的可能性：

使用以下代码块计算雾霾的可能性：

for i, d in enumerate(doy_range):
   indices = np.where(d == doy)
   selection = visibility[indices]

   mist_truth = (10 < selection) & (selection < 20)
   mist[i] = len(selection[mist_truth])/(1\. * len(selection))

   haze_truth = (20 < selection) & (selection < 50)
   haze[i] = len(selection[haze_truth])/(1\. * len(selection))

使用此代码段获取年度计数：

for year in y_range:
   indices = np.where(year == years)
   selection = visibility[indices]
   y_counts[year - 1901] = len(selection[selection > 79])

Refer to the following plot for the end result:

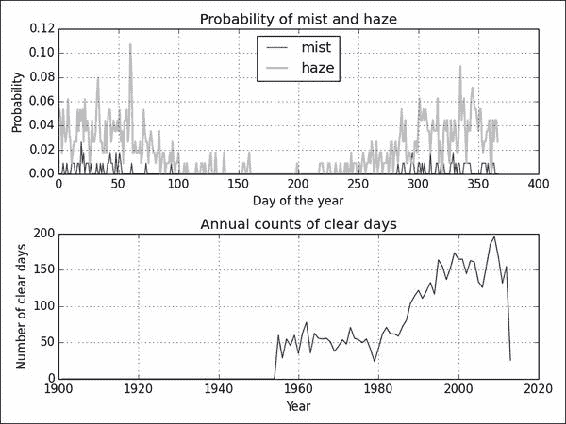
How to do it...

工作原理

如您所见，我们在 1950 年以后开始变得晴朗。这不是由于 1950 年之前的大雾天气，而是由于数据丢失或无效的现象。去年的下降也是由于数据不完整。 1980 年以后，晴天明显增加。这应该是全球变暖和气候变化也加剧的时期。不幸的是，我们没有与空气污染直接相关的数据，但是我们的探索性分析表明存在趋势。

薄雾似乎主要发生在一年的头两个月中。您可以得出有关雾霾的类似结论。显然，雾气比雾气更有可能，这可能是一件好事。您也可以绘制直方图以确保。但是，请记住，正如我之前提到的，您需要忽略0值。

另见

“探索气压”秘籍
“研究年度气压平均值”秘籍
相关维基百科页面

使用自回归模型预测气压

非常简单的预测模型会获取变量的当前值，并将其外推到下一个周期。为了推断，我们可以使用一个简单的数学函数。由于可以通过多项式近似泰勒级数中的多项式，因此低阶多项式可以解决问题。归结为将先前值回归到下一个值。因此，相应的模型称为自回归。

我们必须对此谨慎，以免过拟合。 交叉验证是一种常见的方法，将数据分为训练和测试集。我们使用训练集拟合数据，并使用测试集测试拟合度。这样可以减少偏差（请参见本书代码包中的autoregressive.py文件）：

from __future__ import print_function
import numpy as np
import matplotlib.pyplot as plt

data = np.load('cbk12.npy')

# Load average pressure
meanp = .1 * data[:,1]

# Split point for test and train data
cutoff = 0.9 * len(meanp)

for degree, marker in zip(xrange(1, 4), ['o', 'x','.']):
   poly = np.polyfit(meanp[:cutoff - 1], meanp[1:cutoff], degree)
   print('Polynomial coefficients', poly)

   fit = np.polyval(poly, meanp[cutoff:-1])
   error = np.abs(meanp[cutoff + 1:] - fit)/fit
   plt.plot(error, marker, color=str(.25* degree), label='Degree ' + str(degree))
   plt.plot(np.full(len(error), error.mean()), lw=degree, label='Mean for degree ' + str(degree))

   print("Absolute mean relative error", error.mean(), 'for polynomial of degree', degree)
   print()

plt.title('Relative test errors for polynomial fits')
plt.ylabel('Relative error')
plt.grid()
plt.legend(loc='best')
plt.show()

操作步骤

通过执行以下，我们将使用不同程度的多项式拟合气压：

定义测试和训练集的截止：
```
cutoff = 0.9 * len(meanp)
```

使用polyfit()和polyval()函数拟合数据：

poly = np.polyfit(meanp[:cutoff - 1], meanp[1:cutoff], degree)
print('Polynomial coefficients', poly)

fit = np.polyval(poly, meanp[cutoff:-1])

计算相对误差：

error = np.abs(meanp[cutoff + 1:] - fit)/fit

此代码输出以下输出：

Polynomial coefficients [ 0.995542    4.50866543]
Absolute mean relative error 0.00442472512506 for polynomial of degree 1

Polynomial coefficients [ -1.79946321e-04   1.17995347e+00   2.77195814e+00]
Absolute mean relative error 0.00421276856088 for polynomial of degree 2

Polynomial coefficients [  3.17914507e-06  -6.62444552e-03   4.44558056e+00   2.76520065e+00]
Absolute mean relative error 0.0041906802632 for polynomial of degree 3

Refer to the following plot for the end result:

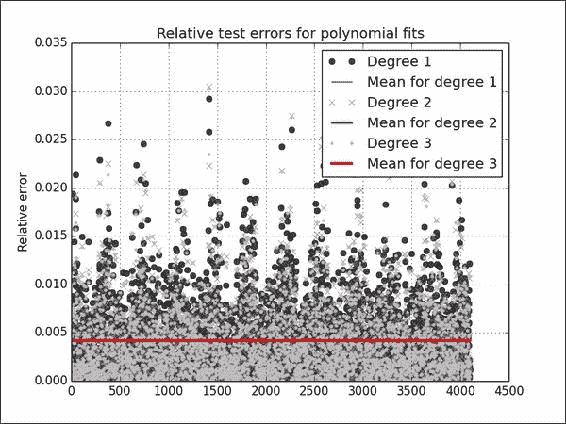
How to do it...

工作原理

这三个多项式的平均相对误差非常接近 -- 约 .004 -- 因此我们在图中看到一条线（很有趣的是知道气压的典型测量误差是多少），小于百分之一。我们看到了一些潜在的异常值，但是没有太多。大部分繁重的工作都是通过polyfit()和polyval()函数完成的，它们分别将数据拟合到多项式并求值该多项式。

另见

使用移动平均模型预测气压

模拟气压的简单方法是假设值围绕均值μ跳动。然后，在最简单的情况下，我们假设连续值与平均值的偏差ε遵循以下公式：

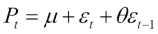
Predicting pressure with a moving average model

该关系是线性的，在最简单的情况下，我们只需要估计一个参数 - θ。为此，我们将需要 SciPy 功能。该秘籍的完整代码在本书代码包的moving_average.py文件中：

from __future__ import print_function
import numpy as np
import matplotlib.pyplot as plt
from datetime import datetime as dt
from scipy.optimize import leastsq

data = np.load('cbk12.npy')

# Load average pressure
meanp = .1 * data[:,1]

cutoff = 0.9 * len(meanp)

def model(p, ma1):
   return p * ma1

def error(p, t, ma1):
   return t - model(p, ma1)

p0 = [.9]
mu = meanp[:cutoff].mean()
params = leastsq(error, p0, args=(meanp[1:cutoff] - mu, meanp[:cutoff-1] - mu))[0]
print(params)

abs_error = np.abs(error(params, meanp[cutoff+1:] - mu, meanp[cutoff:-1] - mu))
plt.plot(abs_error, label='Absolute error')
plt.plot(np.full_like(abs_error, abs_error.mean()), lw=2, label='Absolute mean error')
plt.title('Absolute error for the moving average model')
plt.ylabel('Absolute error (hPa)')
plt.grid()
plt.legend(loc='best')
plt.show()

入门

如有必要，请按照第 2 章，“高级索引和数组概念”的“安装 SciPy”秘籍中的说明安装 SciPy。

操作步骤

以下步骤将移动平均模型应用于气压。

定义以下函数：

def model(p, ma1):
   return p * ma1

def error(p, t, ma1):
   return t - model(p, ma1)

使用上一步中的函数将移动平均模型与leastsq()函数拟合，并将0.9的初始猜测作为模型参数：

p0 = [.9]
mu = meanp[:cutoff].mean()
params = leastsq(error, p0, args=(meanp[1:cutoff] - mu, meanp[:cutoff-1] - mu))[0]

使用测试数据集拟合后计算绝对误差：
```
abs_error = np.abs(error(params, meanp[cutoff+1:] - mu, meanp[cutoff:-1] - mu))
```
请参考以下数据集中每个数据点的绝对误差图：

工作原理

leastsq()函数通过最小化误差来拟合模型。它需要一个函数来计算拟合误差和模型参数的初始猜测。

另见

研究年内平均气压

在一年内探索气压很有趣。特别地，检查与变异性相关的模式可能是有益的，因此，与可预测性相关。原因是几个月中的气气压会发生很大变化，从而降低了可预测性。在此秘籍中，我们将绘制每月的箱形图和每月的气气压方差。

秘籍代码在本书代码包的intrayear.py文件中。请特别注意突出显示的部分：

import numpy as np
import matplotlib.pyplot as plt
import calendar as cal

data = np.load('cbk12.npy')

# Multiply to get hPa values
meanp = .1 * data[:,1]

# Get months
dates = data[:,0]
months = (dates % 10000)/100

monthly = []
vars = np.zeros(12)
month_range = np.arange(1, 13)

for month in month_range:
 indices = np.where(month == months)
 selection = meanp[indices]

 # Filter out 0 values
 selection = selection[selection > 0]

 monthly.append(selection)
 vars[month - 1] = np.var(selection)

def plot():
    plt.xticks(month_range, cal.month_abbr[1:13])
    plt.grid()
    plt.xlabel('Month')

plt.subplot(211)
plot()
plt.title('Atmospheric pressure box plots')
plt.boxplot(monthly)
plt.ylabel('Atmospheric pressure (hPa)')

plt.subplot(212)
plot()

# Display error bars using standard deviation
plt.errorbar(month_range, vars, yerr=vars.std())
plt.plot(month_range, np.full_like(month_range, np.median(vars)), lw=3, label='Median')

# Shades the region above the median
plt.fill_between(month_range, vars, where=vars>np.median(vars), color='0.5')
plt.title('Variance of atmospheric pressure')
plt.ylabel('Variance')
plt.legend(loc='best')

plt.show()

操作步骤

在我们探索时，往往会重复这些步骤，并且此秘籍与本书中的其他秘籍之间存在重叠。以下是此秘籍中的新步骤：

使用标准差显示误差线：

plt.errorbar(month_range, vars, yerr=vars.std())

用高于中值的值对图的区域进行着色：
```
plt.fill_between(month_range, vars, where=vars>np.median(vars), color='0.5')
```
Refer to the following plot for the end result:

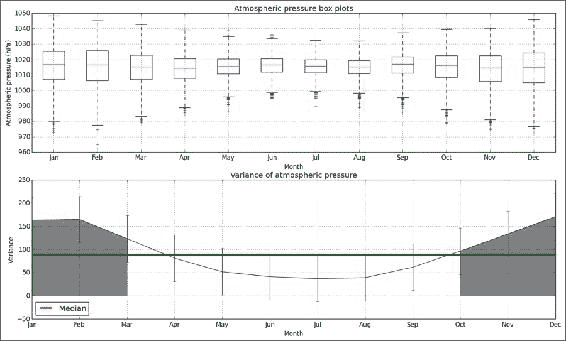
工作原理

我们将几个月与气气压的测量相匹配。我们使用匹配来绘制箱形图并可视化每月变化。这项研究表明，在 1 月，2 月，11 月和 12 月的最冷月份，气压变化高于中值。从图中可以看出，在温暖的夏季，气压范围狭窄。这与其他秘籍的结果一致。

另见

“探索气压”秘籍
“研究年度气压平均值”秘籍
var()的文档

研究气压的极值

异常值是一个问题，因为它们会影响我们对数据的理解。在此秘籍中，我们将异常值定义为与数据的第一或第三四分位数相差至少四分位数范围的 1.5 倍。四分位数间距是第一和第三四分位数之间的距离。让我们计算一年中每个月的异常值。完整的代码在本书代码包的extreme.py文件中：

import numpy as np
import matplotlib.pyplot as plt
import calendar as cal

data = np.load('cbk12.npy')

# Multiply to get hPa values
meanp = .1 * data[:,1]

# Filter out 0 values
meanp = np.ma.array(meanp, mask = meanp == 0)

# Calculate quartiles and irq
q1 = np.percentile(meanp, 25)
median = np.percentile(meanp, 50)
q3 = np.percentile(meanp, 75)

irq = q3 - q1

# Get months
dates = data[:,0]
months = (dates % 10000)/100

m_low = np.zeros(12)
m_high = np.zeros(12)
month_range = np.arange(1, 13)

for month in month_range:
   indices = np.where(month == months)
   selection = meanp[indices]
   m_low[month - 1] = len(selection[selection < (q1 - 1.5 * irq)])
   m_high[month - 1] = len(selection[selection > (q3 + 1.5 * irq)])

plt.xticks(month_range, cal.month_abbr[1:13])
plt.bar(month_range, m_low, label='Low outliers', color='.25')
plt.bar(month_range, m_high, label='High outliers', color='0.5')
plt.title('Atmospheric pressure outliers')
plt.xlabel('Month')
plt.ylabel('# of outliers')
plt.grid()
plt.legend(loc='best')
plt.show()

操作步骤

要绘制一年中每个月的异常数，请执行以下步骤：

使用percentile()函数计算四分位数和四分位数间距：

q1 = np.percentile(meanp, 25)
median = np.percentile(meanp, 50)
q3 = np.percentile(meanp, 75)

irq = q3 - q1

计算异常值的数量，如下所示：

for month in month_range:
   indices = np.where(month == months)
   selection = meanp[indices]
   m_low[month - 1] = len(selection[selection < (q1 - 1.5 * irq)])
   m_high[month - 1] = len(selection[selection > (q3 + 1.5 * irq)])

Refer to the following plot for the end result:

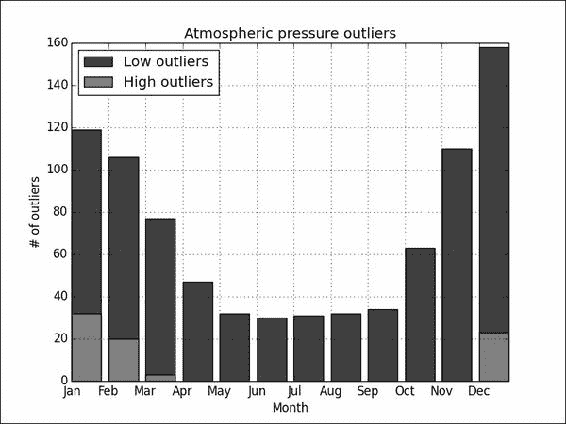
How to do it...

工作原理

看起来异常值大多在下侧，并且夏天不太可能出现。较高端的异常值似乎仅在某些月份内发生。我们发现四分位数具有percentile()函数，因为四分之一对应 25%。

另见

“探索气压”秘籍
percentile()函数的文档

标签：11,12,meanp,selection,print,range,plt,np,NumPy
From： https://www.cnblogs.com/apachecn/p/17311646.html

NumPy 秘籍中文第二版：11~12

十一、最新最强的 NumPy

简介

使用at()方法为 ufuncs 建立花式索引

操作步骤

另见

使用partition()函数通过快速中位数的选择进行部分排序

注意

操作步骤

工作原理

另见

使用nanmean()，nanvar()和nanstd()函数跳过 NaN

操作步骤

工作原理

另见

使用full()和full_like()函数创建初始化值的数组

操作步骤

工作原理

使用numpy.random.choice()进行随机采样

操作步骤

工作原理

另见

使用datetime64类型和相关的 API

操作步骤

工作原理

另见

十二、使用 NumPy 进行探索性和预测性数据分析

简介

探索气压

准备

操作步骤

另见

探索日常气压范围

操作步骤

工作原理

另见

研究年度气压平均值

操作步骤

工作原理

另见

分析最大可见度

操作步骤

工作原理

另见

使用自回归模型预测气压

操作步骤

工作原理

另见

使用移动平均模型预测气压

入门

操作步骤

工作原理

另见

研究年内平均气压

操作步骤

工作原理

另见

研究气压的极值

操作步骤

工作原理

另见

相关文章

赞助商

阅读排行

使用`at()`方法为 ufuncs 建立花式索引

使用`partition()`函数通过快速中位数的选择进行部分排序

使用`nanmean()`，`nanvar()`和`nanstd()`函数跳过 NaN

使用`full()`和`full_like()`函数创建初始化值的数组

使用`numpy.random.choice()`进行随机采样

使用`datetime64`类型和相关的 API