标签：prd int 短路路径 rightsquigarrow 笔记删边 mathrm

删边最短路

前言

删边最短路是一种科技，用于解决一类问题：

给定非负权图 \(G = (V, E)\)。设 \(n = |V|\)，保证 \(1\) 可达 \(n\)。

设 \(\Delta(e)\) 为图 \(G' = (V, E \setminus \{e\})\) 上 \(1 \rightsquigarrow n\) 的最短路，若 \(G'\) 上 \(1\) 不可达 \(n\) 则为 \(+\infty\)。

对每个 \(e \in E\)，求出 \(\Delta(e)\)。

点的编号不影响什么，源点和终点可以随便给，这里给 \(1\) 和 \(n\) 是为方便。

我将删边最短路称为科技，是因为删边最短路的整个流程逻辑链相对复杂，难以想到，重在积累。

所以本文只会描述删边最短路科技的过程以及必要的证明，而不会阐述一些东西是怎么想到的。

前置知识：最短路树的定义与构建。

本文中 \(w(e)\) 代表边 \(e\) 的权值，\(w(u, v)\) 代表 \((u, v)\) 这条边的权值，\(w(P)\) 代表路径 \(P\) 的权值。

同时请注意“最短路”和“最短路径”的差别，前者指的是长度，后者指的是路径。

无向图

即保证 \(G\) 是无向的。

这里再加一个限制条件：\(G\) 是联通图，可以简化讨论。

\(G\) 不是联通图的情况，显然除了 \(1\) 和 \(n\) 所在联通块，其他联通块可以直接忽略。

前提记号

设 \(G\) 的以 \(1\) 为根的任意一棵最短路树 \(T\)，并从 \(T\) 上找到 \(1 \rightsquigarrow n\) 的路径，设为 \(P\)。

注意，\(1 \rightsquigarrow n\) 的最短路径可能有很多，这里 \(T\) 上的那条 \(1 \rightsquigarrow n\) 的路径和 \(P\) 必须是原图上同一条最短路径。

设 \(P = p_0(=1) \xrightarrow{E_1}p_1 \xrightarrow{E_2}p_2\xrightarrow{E_3}\cdots\xrightarrow{E_k}p_k(=n)\)，\(V_P = \{p_i\}\)，\(E_P = \{E_i\}\)，\(D = w(P) = \sum E_i\)。

显然，从 \(T\) 上选出的 \(1 \rightsquigarrow n\) 最短路径一定是简单的（不包含零环），因此上面的 \(p_i\)，\(E_i\) 都互不相同。

原图上 \(1 \rightsquigarrow u\)，以及 \(u \rightsquigarrow n\) 之间可能有许多条最短路径，那么这里我们规定：

给定 \(u\)，对于 \(1 \rightsquigarrow u\) 的最短路径，指的是 \(T\) 上 \(1 \rightsquigarrow u\) 这段路径代表的最短路径，设为 \(P(1, u)\)。
给定 \(u\)，对于 \(u \rightsquigarrow n\) 的最短路径，指的是 \(T\) 上 \(u \rightsquigarrow n\) 这段路径代表的最短路径。设为 \(P(u, n)\)。
同时，设 \(D(1, u) = w(P(1, u))\)，\(D(u, n) = w(P(u, n))\)。
于是事实上，\(P\) 可以看做 \(P(1, n)\) 的简写；\(D\) 可以看做 \(D(1, n)\) 的简写。

另外，对于任意 \(u \in V_P\)，记 \(u\) 在 \(p\) 上的下标为 \(\mathrm{id}(u)\)。即，\(p_{\mathrm{id}(u)} = u\)。

引理

\(\mathbf{Lemma\ 1}\) 对于任意 \(\boldsymbol{e \not\in E_P}\)，\(\boldsymbol{\Delta(e) = D}\)。

删除 \(e\) 不会影响最短路径 \(P\)，也不可能凭空生成一条距离更小的路径，因此 \(1\) 到 \(n\) 的最短路仍然是 \(D\)。

这个引理告诉我们，只需关心 \(e \in E_P\) 的 \(\Delta(e)\) 即可。

\(\mathbf{Lemma\ 2.1}\) 对于任意 \(\boldsymbol {u \ne v}\)，\(\boldsymbol{P(1, u)}\) 和 \(\boldsymbol{P(1, v)}\) 只会共享一段前缀（可以只有 \(\boldsymbol 1\) 一个点），然后走互不相交的道路。

\(\mathbf{Lemma\ 2.2}\) 对于任意 \(\boldsymbol{u \ne v}\)，\(\boldsymbol{P(u, n)}\) 和 \(\boldsymbol{P(v, n)}\) 只会共享一段后缀（可以只有 \(\boldsymbol n\) 一个点），之前一定走互不相交的道路。

\(\mathbf{Lemma\ 2.3}\) 对于任意 \(\boldsymbol{0 \le i \le k}\)，\(\boldsymbol{P(1, p_i)}\) 是 \(\boldsymbol P\) 的一段前缀，\(\boldsymbol{P(p_i, n)}\) 是 \(\boldsymbol P\) 的一段后缀。

\(P(1, u)\)，\(P(1, v)\)，\(P(u, n)\)，\(P(v, n)\) 都是从最短路树上摘出来的。

根据树的性质，自然有 \(1\) 到 \(u\) 的路径和 \(1\) 到 \(v\) 的路径只共享一段前缀，然后分叉。\(u\) 到 \(n\) 的路径和 \(v\) 到 \(n\) 的路径同理。

第三条是因为在 \(T\) 上，\(p_i\) 在 \(1\) 和 \(n\) 之间的链上。

\(\mathbf{Lemma\ 3.1}\) 一条最短路径的任意一段子路径，也是一条以这条子路径两端为源点和终点的最短路径。

一条最短路径 \(P'\) 的任意子路径 \(Q\) 也是一条最短路径。否则，若存在长度比 \(Q\) 短（且源点终点相同）的另一路径 \(Q'\)，则 \(P’\) 可以将自身的子路径 \(Q\) 替换为 \(Q'\) 从而生成更短的路径，与 \(P'\) 是最短路径矛盾。

\(\mathbf{Lemma\ 3.2}\) 对于 \(\boldsymbol{e \in E_P}\)，删除 \(\boldsymbol e\) 后，\(\boldsymbol 1\) 到 \(\boldsymbol n\) 若可达，则存在一条 \(\boldsymbol 1\) 到 \(\boldsymbol n\) 的简单最短路径，满足该路径从 \(\boldsymbol 1\) 开始，先跟 \(\boldsymbol P\) 共享一段前缀（可以只有 \(\boldsymbol 1\) 一个点），然后腾空一段绕过 \(\boldsymbol e\)（期间与 \(\boldsymbol P\) 无交），最后和 \(\boldsymbol P\) 共享一段后缀（可以只有 \(\boldsymbol n\) 一个点）到达 \(\boldsymbol n\)。

删除 \(e\) 后 \(1\) 仍可达 \(n\)，则随便生成一条最短路径 \(Q'\)（若可达，则一定存在最短路径）。

考虑删除 \(Q'\) 上的全部零环，就可以得到一条简单最短路径 \(Q'\)。

设 \(Q'\) 从 \(1 \rightsquigarrow n\)，其与 \(P\) 的所有交点一定都属于 \(V_P\)。

令 \(A\) 为 \(Q'\) 先后与 \(P\) 形成的交点的 \(\mathrm{id}\) 构成的序列。因为 \(Q'\) 从 \(p_0 = 1\) 开始，到 \(p_k = n\) 结束，所以 \(A\) 首项为 \(0\)，末项为 \(k\)。

设 \(A\) 的长度为 \(L\)，则 \(Q'\) 可以表示成 \(p_{A_1}(=1) \rightsquigarrow p_{A_2} \rightsquigarrow p_{A_3} \rightsquigarrow \cdots\rightsquigarrow p_{A_L}(=n)\)。

设删除的边 \(e = E_t = (p_{t-1}, p_{t})\)，明显有 \(1 \le t \le k\)。

【内置小命题】存在一个 \(1 \le i < L\)，使得 \(A_i \le t - 1\) 且 \(A_{i + 1} \ge t\)。

简记判断条件 \(C(i) = A_i \le t - 1 \land A_{i + 1} \ge t\)。（\(\land\) 是且）。

如果存在一个 \(1 \le i < L - 1\) 的 \(i\)，使得 \(C(i)\) 为真，命题直接成立。

否则，对于任意 \(1 \le i < L - 1\) 的 \(i\)，\(C(i)\) 均为假。则：

\(i = 1\) 时，\(C(1)\) 为假，而 \(A_1 = 0 \le t - 1\)，因此 \(A_{i +1} \ge t\) 为假，即 \(A_2 \le t - 1\)。

\(i = 2\) 时，\(C(2)\) 为假，而 \(A_2 \le t - 1\)，因此 \(A_{i +1} \ge t\) 为假，即 \(A_3 \le t - 1\)。

……

依次类推，\(i = L - 2\) 时，\(C(L - 2)\) 为假，而 \(A_{L - 2} \le t - 1\)，因此 \(A_{i + 1} \ge t\) 为假，即 \(A_{L - 1} \le t - 1\)。

不难发现，因为 \(A_{L - 1} \le t - 1\)，\(A_L = k \ge t\)，所以 \(i = L - 1\) 时 \(C(i)\) 为真，找到 \(i\)，小命题得证。

【内置小命题证明结束】

根据内置小命题找到这个 \(i\)，记 \(Q'(p_{A_i} \rightsquigarrow p_{A_{i + 1}})\) 为 \(Q'\) 中表示 \(p_{A_i} \rightsquigarrow p_{A_{i + 1}}\) 的子路径。

由于 \(A_i \le t - 1\)，因此 \(P(1, p_{A_i})\) 不经过 \(e\)。由于 \(A_{i +1} \ge t\)，因此 \(P(p_{A_{i +1}}, n)\) 也不经过 \(e\)。

因此删 \(e\) 后，\(1 \rightsquigarrow p_{A_i}\) 仍然存在最短路径 \(P(1, p_{A_i})\)，\(p_{A_{i +1}} \rightsquigarrow n\) 仍然存在最短路径 \(P(p_{A_{i +1}}, n)\)。

构造路径 \(Q = P(1, p_{A_i}) \cup Q'(p_{A_i} \rightsquigarrow p_{A_{i + 1}}) \cup P(p_{A_{i + 1}}, n)\)。

这里我们只是把 \(Q'\) 这个最短路径中的两条子路径替换成了另外两条最短路径，因此 \(Q\) 也是合法的删边最短路径。

然后考虑 \(Q'(p_{A_i} \rightsquigarrow p_{A_{i + 1}})\)。

由于 \(A_i\) 和 \(A_{i +1}\) 是 \(A\) 中相邻的两个元素，证明 \(Q'\) 从 \(p_{A_i}\) 来到 \(p_{A_{i + 1}}\) 的过程中，中间不再和 \(P\) 有其他交点。

所以 \(Q\) 和 \(P\) 共享一段前缀 \(P(1, p_{A_i})\)，一段后缀 \(P(p_{A_{i +1}}, n)\)，中间 \(Q'(p_{A_i} \rightsquigarrow p_{A_{i + 1}})\) 的部分腾空而起，满足条件，构造成功。

\(\mathbf{Lemma\ 4}\) **对于 \(\boldsymbol{e \in E_P}\)，删除 \(\boldsymbol e\) 后，\(\boldsymbol 1\) 到 \(\boldsymbol n\) 若可达，根据 \(\mathbf {Lemma\ 3.2}\) 构造出的 \(\boldsymbol 1\) 到 \(\boldsymbol n\) 的删边简单最短路径中，存在一条最短路径，不在 \(\boldsymbol{T}\) 上的边有且只有一条。 **

【注】这条引理只在无向图上成立，无法推广到有向图。

定义树边为在 \(T\) 上的边，非树边为不在 \(T\) 上的边。

两条比较显然的事实：

这里 \(T\) 上 \(1\) 和 \(n\) 之间不再连通了，所以新的删边最短路径必须经过一条非树边。
\(P(1, u)\)，\(P(u, n)\) 路径上的边都是树边（因为本来就是从 \(T\) 上摘出来的）。

设 \(\mathrm{pre}(u)\) 表示 \(P(1, u)\) 和 \(P\) 的最后一个交点，也即 \(n\) 和 \(u\) 在 \(T\) 上的 LCA。

显然 \(\mathrm{pre}(u) \in V_P\)。设 \(\mathrm{prd}(u) = \mathrm{id(pre}(u))\)。

仍然令删去的边 \(e = E_i = (p_{i - 1}, p_i)\)。

先根据 \(\mathbf {Lemma\ 3.2}\) 构造出 \(1\) 到 \(n\) 的一条删边简单最短路径 \(Q'\)。它和 \(P\) 共享前缀和后缀，中间腾空而起，但不保证非树边数量。

如果 \(Q'\) 上非树边数量为一，则构造直接成功。

否则考虑 \(Q'\) 上第一条非树边 \((a, b)\)，其中 \(a\) 靠近 \(1\) 一端，\(b\) 靠近 \(n\) 一端，如下图所示。

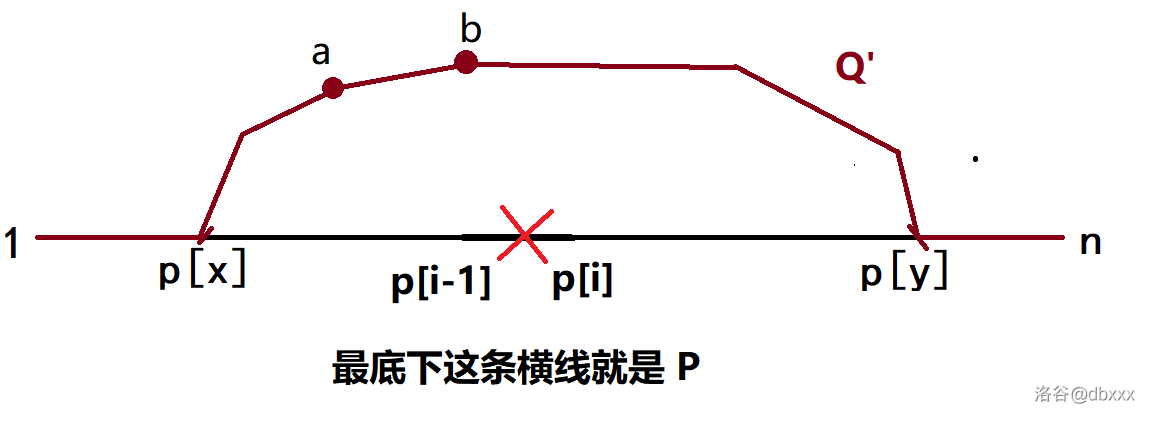
如果 \(\mathrm{pre}(b)\) 落在 \(p_i\) 及其左侧，即 \(\mathrm{prd}(b) \le i\)，那么 \(P(1, b)\) 不经过 \(e\)。

直接将 \(Q'\) 中 \(1 \rightsquigarrow b\) 的部分替换成 \(P(1, b)\)，就可以删除 \((a, b)\) 这条非树边。

下图中，橙色的路径就是替换后的新 \(Q'\)。注意下图中 \(\mathrm{pre}(b)\) 和 \(b\) 之间是一条路径，可能有多条边，这里简化成直线了。

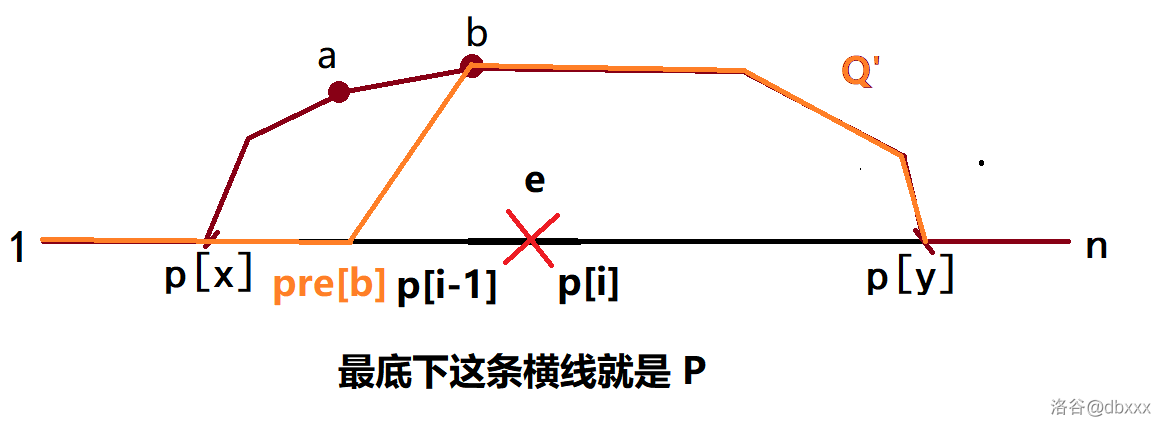
如果替换后的新 \(Q'\) 非树边数量为一，构造成功；

否则，如果替换后的新 \(Q'\) 的第一条非树边 \((a, b)\) 仍然满足 \(\mathrm{pre}(b)\) 落在 \(p_i\) 及其左侧，则再次用 \(P(1, b)\) 替换 \(\mathrm{pre}(b)\)。

重复上述步骤，一直到新 \(Q'\) 的第一条非树边 \((a, b)\) 满足 \(\mathrm{pre}(b)\) 落在 \(p_{i + 1}\) 及其右侧为止，即 \(\mathrm{prd}(b) \ge i +1\)。

这时，\(P(\mathrm{pre}(b), n)\) 不经过 \(e\)。直接将 \(Q'\) 中 \(b \rightsquigarrow n\) 替换成 \(b \rightsquigarrow \mathrm{pre}(b) \cup P(\mathrm{pre}(b), n)\) 即可。

这里 \(b \rightsquigarrow \mathrm{pre}(b)\) 必须是 \(P(1, b)\) 上的子路径。如下图：

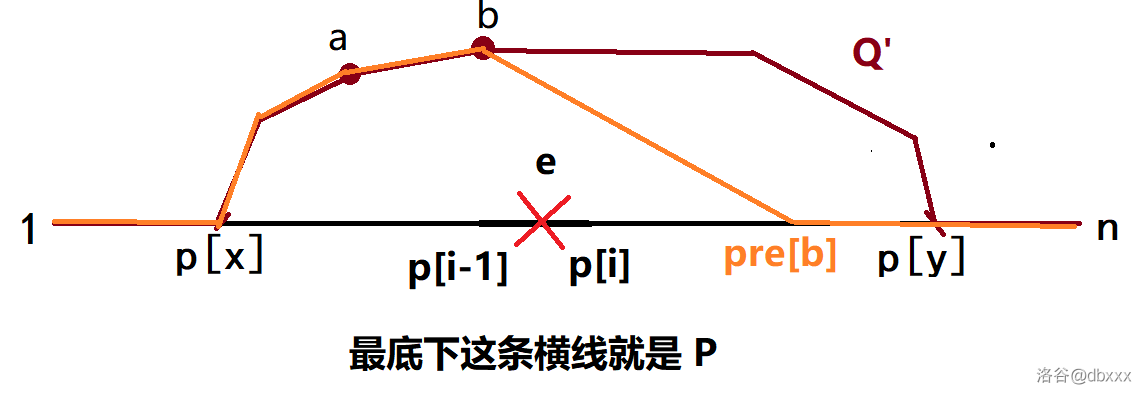
这个时候，新的橙色路径 \(Q'\) 已经满足只有一条非树边 \((a, b)\)，至此构造成功。

注意到，上面第二个分支的构造中，用到了无向图中路径的双向性：原本 \(P(1, b)\) 的子路径是 \(\mathrm{pre}(b) \rightsquigarrow b\)，而构造的路径却反着走了这条路径，方向是 \(b \rightsquigarrow \mathrm{pre}(b)\)。

因此类似证明搬到有向图是不成立的，事实上结论也不成立，后面会给出反例。

\(\mathbf{Lemma\ 5}\) \(\boldsymbol{\Delta(E_i) = \min\{D(1, a) + w(a, b) + D(b, n) \mathop | (a, b) \in E \setminus E_P ,\mathrm{prd}(a) \le i - 1 < i \le \mathrm{prd}(b) \}}\)。特别地，这里表示边的二元组 \(\boldsymbol{(a, b)}\) 是有序数对，需按照 \(\boldsymbol{\mathbf{prd}(a) \le \mathbf{prd}(b)}\) 调整顺序。

同理，后文提到边 \((a, b)\) 的时候，默认 \(\mathrm{prd}(a) \le \mathrm{prd}(b)\)。否则交换一下 \(a\) 和 \(b\) 就好了。

\(\mathbf{Lemma\ 4}\) 告诉我们，对于任意 \(e \in E_P\)，只要删去 \(e\) 后 \(1\) 可达 \(n\)，就一定存在一条删 \(e\) 最短路径满足上面恰好有一条非树边。

更进一步，只要删去 \(e = E_i\) 后 \(1\) 可达 \(n\)，则一定能找到一条满足 \(\mathrm{prd}(a) \le i - 1 < i \le \mathrm{prd}(b)\) 的非树边 \((a, b)\)，且对应的路径 \(1 \rightsquigarrow \mathrm{pre(a)} \rightsquigarrow a \to b \rightsquigarrow \mathrm{pre}(b) \rightsquigarrow n\) 是一条满足题意的删 \(e\) 最短路径。其中只有 \(a \to b\) 是一条非树边，其余都是最短路树上的路径。

不难发现上面这条路径的长度等于 \(D(1, a) + w(a, b) + D(b, n)\)。

也就是说，设 \(S\) 为所有满足 \(\mathrm{prd}(a) \le i - 1 < i \le \mathrm{prd}(b)\) 的非树边 \((a, b)\) 对应的所有 \(D(1, a) + w(a, b) + D(b, n)\) 构成的集合，则 \(\Delta(e) \in S\)。

考虑 \(\Delta(e)\) 是删 \(e\) 最短路，而 \(S\) 中所有的值都至少是删 \(e\) 后形成的某条合法路径总权值，所以 \(\Delta(e) = \min(S)\)。也即，

设 \(E_T\) 为最短路树上的边集，则

\[\Delta(E_i) = \min\{D(1, a) + w(a, b) + D(b, n) \mathop | (a, b) \in E \setminus E_T,\mathrm{prd}(a) \le i - 1 < i \le \mathrm{prd}(b) \} \]

接下来的目标就是试图将 \((a, b)\) 的范围从 \(E \setminus E_T\) 扩大到 \(E \setminus E_P\)，也就是考虑把不在 \(P\) 上的树边放进来。

大概绘制一下最短路树的形态例：

不难发现，不在 \(P\) 上的树边 \((a, b)\)，都满足 \(\mathrm{prd}(a) = \mathrm{prd}(b)\)。因此 \(\mathrm{prd}(a) \le i - 1 < i \le \mathrm{prd}(b)\) 这个条件无法成立。

所以前一个条件把这些边放进来也无所谓，这些边一定通不过后面那个条件。

算法流程

准备工作

首先，在原图上以源点 \(1\) 跑 dijkstra，得到以 \(1\) 为根的最短路树 \(T\)，\(P\)，\(D\)，\(D(1, u)\)。

然后，在原图上以源点 \(n\) 跑 dijkstra，得到每个点 \(u\) 距离 \(n\) 的最短距离 \(D(u, n)\)。

然后考虑根据 \(T\) 求出 \(\mathrm{pre}(u)\)。当然可以倍增 LCA，但是由于我们要批量求解 \(\mathrm{LCA}(u, n)\)，\(n\) 是定点。

所以我们可以考虑将 \(T\) 上 \(1 \rightsquigarrow n\) 这条链，即 \(P\) 上的边全部断掉。

这样会形成森林（可能有孤立点），而且每棵树应恰有一个点属于 \(V_P\)，设这个点为这棵树的根。

于是对于每个点 \(u\)，\(\mathrm{pre}(u) = \mathrm{LCA}(u, n)\) 就是 \(u\) 所在的树根。

还是以这个图为例：

我们断掉 \(P\) 上的边，得到：

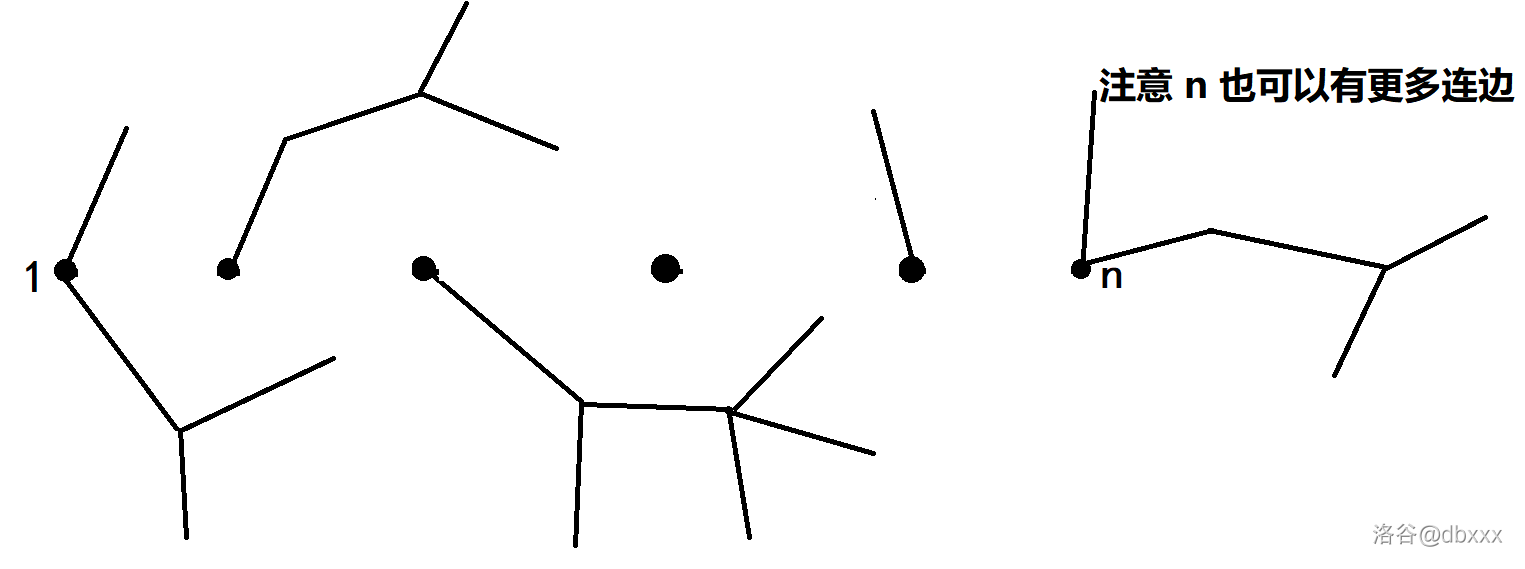
实心黑点对应 \(V_P\) 上的某个点，设其为所在树的根。不难发现，对于每个点 \(u\)，\(\mathrm{pre}(u) = \mathrm{LCA}(u, n)\) 就是 \(u\) 所在的树根。

不过由于后面要用到的是 \(\mathrm{prd}\)，所以可以直接求 \(\mathrm{prd}\)，即树根的 \(\mathrm{id}\)。具体看下面例题代码。

另外注意，可以有点的 \(\mathrm{prd}\) 是 \(0\)，也即 \(\mathrm{pre}\) 为 \(p_0 = 1\) 的点。

维护与计算

根据强大的 \(\mathrm{Lemma\ 1}\)，对于任何 \(e \not\in E_P\)，\(\Delta(e) = D\)。

根据强大的 \(\mathrm{Lemma\ 5}\)，对于任何 \(e \in E_P\)，设 \(e = E_i\)，有：

\[\Delta(E_i) = \min\{D(1, a) + w(a, b) + D(b, n) \mathop | (a, b) \in E \setminus E_P,\mathrm{prd}(a) \le i - 1 < i \le \mathrm{prd}(b) \} \]

然而直接求解，时间复杂度太高了。

考虑对于一条非 \(E_P\) 边 \((a, b)\)，不难发现，它只会贡献满足 \(\mathrm{prd}(a) + 1 \le i \le \mathrm{prd}(b)\) 的 \(E_i\)，下标是一段区间。

因此可以得到下面的问题简化：

初始定义 \(\mathrm{ans}(i) = +\infty\)。
对于每条非 \(E_P\) 边 \((a, b)\)，对下标在 \([\mathrm{prd}(a) +1, \mathrm{prd}(b)]\) 范围内的 \(\mathrm{ans}\) 与 \(D(1, a) + w(a, b) + D(b, n)\) 区间取 \(\min\)。
- 这里如果发现 \(\mathrm{prd}(a) = \mathrm{prd}(b)\) 直接特判忽略这个边的贡献。
最后 \(\mathrm{ans}(i) = \Delta(E_i)\)。如果某个 \(\mathrm{ans}(i)\) 仍然是 \(+\infty\)，证明断掉 \(E_i\) 后 \(1 \rightsquigarrow n\) 不可达。

可以线段树，先进行所有区间取 \(\min\)，然后回答时对 \(\mathrm{ans}(i)\) 的单点在线查询。

因为询问都在区间操作之后，也可以先预处理出所有 \(\mathrm{ans}(i)\)，最后 \(\Theta(1)\) 回答 \(\Delta(e)\) 的询问。这样可以离线 multiset 扫描线。

具体来说，\(i\) 从 \(1 \rightsquigarrow k\) 求解 \(\mathrm{ans}(i)\)，维护 multiset 上的最小值。

求解 \(\mathrm{ans}(i)\) 之前，先在 multiset 中撤销右端点位于 \(i - 1\) 的区间 \(\min\) 操作；再加入所有左端点位于 \(i\) 的区间 \(\min\) 操作，最后取 multiset 的 \(\min\) 即可。

或者换个顺序，先加入所有左端点位于 \(i\) 的区间操作，再取 \(\min\) 得到 \(\mathrm{ans}(i)\) 答案，最后撤销右端点位于 \(i\) 的区间操作。

删边最短路就做完了。

时间复杂度

\(\Theta((m + n)\log m + q)\)。

例题

bzoj 2725 [Violet 6]故乡的梦

bzoj 2725。

模板题。不保证图联通，也不保证初始时 \(S\) 和 \(T\) 在同一个连通块。

考虑上述算法小修改一下。

如果 \(S\) 和 \(T\) 不连通，求出的最短路为 \(+\infty\)，此时特判所有询问都输出 Infinity。
\(S\) 和 \(T\) 连通，但图不联通？
不在 \(S\) 和 \(T\) 所在连通块上的边 \(e\) 可以正确地被判断不属于 \(E_P\)，得到 \(\Delta(e) = D\)。
判断不在 \(S\) 和 \(T\) 所在连通块上的点 \(u\)，可以用求解出的 \(1 \rightsquigarrow u\) 的最短路是否有穷判断。
我们令不在 \(S\) 和 \(T\) 所在连通块上的点 \(u\) 的 \(\mathrm{pre}(u)\) 和 \(\mathrm{prd}(u)\) 为 \(-1\)。
这样以来，不在 \(S\) 和 \(T\) 所在连通块上的边 \(e\) 两端 \(\mathrm{prd}\) 相同，会被特判到忽略贡献。

问题就解决了，其实不影响什么。

/*
 * @Author: crab-in-the-northeast 
 * @Date: 2023-04-07 16:01:16 
 * @Last Modified by: crab-in-the-northeast
 * @Last Modified time: 2023-04-07 19:33:06
 */
#include <bits/stdc++.h>
#define int long long
inline int read() {
	int x = 0;
	bool f = true;
	char ch = getchar();
	for (; !isdigit(ch); ch = getchar())
		if (ch == '-')
			f = false;
	for (; isdigit(ch); ch = getchar())
		x = (x << 1) + (x << 3) + ch - '0';
	return f ? x : (~(x - 1));
}

const int maxn = (int)2e5 + 5;
const int maxm = (int)2e5 + 5;
typedef std :: pair <int, int> pii;

std :: vector <pii> G[maxn];
// G[u] 存储一个顶点是 u 的边信息
// pii 第一项为边连接的另一个顶点 v，第二项为边编号
int wei[maxm]; // 记录边编号为 i 的边权

std :: unordered_map <int, int> eid;
// 这个用来根据边两边的点信息还原出边的编号
// 因为 umap 自带哈希函数不支持 pair
// 考虑给键值传个 u * n + v

int fa[maxn], pred[maxn];
// fa[u]：最短路树 T 上 u 的父亲
// pred[u]：最短路树上连接 u 和 fa[u] 的边编号
int dis[maxn], rem[maxn], prd[maxn];
// dis[u] 为 s -> u 最短路，rem[u] (remain) 为 u -> t 最短路
int tag[maxm];
// tag[i] 记录 i 编号这条边在 E 上的下标，如果不在 E_P 上则为 0
int ans[maxn];
// ans[i] 记录删除 E_i 的最短路

std :: vector <int> ls[maxn];
std :: vector <int> rs[maxn];
// ls[i] 存放左端点在 i 的区间信息，rs[i] 存放右端点在 i 的区间信息

int s, t, n, k; // k 表示最短路 P 的边数

inline int getprd(int u) {
	return prd[u] = (prd[u] != -1 ? prd[u] : getprd(fa[u]));
}

inline bool init() {
	std :: memset(dis, 0x3f, sizeof(dis));
	const int inf = dis[0];
	dis[s] = pred[s] = fa[s] = 0;
	std :: priority_queue <pii> q;
	q.push({0, s});
	while (!q.empty()) {
		int d = q.top().first, u = q.top().second;
		q.pop();
		if (d + dis[u])
			continue;
		for (pii e : G[u]) {
			int v = e.first, id = e.second, w = wei[id];
			if (dis[u] + w < dis[v]) {
				dis[v] = dis[u] + w;
				fa[v] = u;
				pred[v] = id;
				q.push({-dis[v], v});
			}
		}
	}

	if (dis[t] >= inf)
		return false;
	
	std :: vector <int> P; // 这个 P 实际是 V_P
	for (int u = t; u; u = fa[u])
		P.push_back(u);
	std :: reverse(P.begin(), P.end());
	k = (int)P.size() - 1;
	// 在 P 上，点编号 0~k，共 k+1 个；边编号 1~k，共 k 个。
	std :: memset(prd, -1, sizeof(prd));
	for (int i = 0; i <= k; ++i) {
		prd[P[i]] = i;
		tag[pred[P[i]]] = i;
	}

	for (int u = 1; u <= n; ++u) {
		if (dis[u] < inf)
			getprd(u);
	}

	std :: memset(rem, 0x3f, sizeof(rem));
	rem[t] = 0;
	q.push({0, t});
	while (!q.empty()) {
		int d = q.top().first, u = q.top().second;
		q.pop();
		if (d + rem[u])
			continue;
		for (pii e : G[u]) {
			int v = e.first, id = e.second, w = wei[id];
			if (rem[u] + w < rem[v]) {
				rem[v] = rem[u] + w;
				q.push({-rem[v], v});
			}
		}
	}

	return true;
}

signed main() {
	n = read();
	int m = read();
	for (int i = 1; i <= m; ++i) {
		int u = read(), v = read(), w = read();
		G[u].push_back({v, i});
		G[v].push_back({u, i});
		wei[i] = w;
		if (u > v)
			std :: swap(u, v);
		eid[u * n + v] = i;
	}

	s = read(), t = read();
	if (!init()) {
		int q = read();
		while (q--)
			puts("Infinity");
	}
	
	for (int u = 1; u <= n; ++u) {
		for (pii e : G[u]) {
			int v = e.first, id = e.second, w = wei[id];
			if (tag[id])
				continue;
			if (prd[u] < prd[v]) {
				int W = dis[u] + w + rem[v];
				ls[prd[u] + 1].push_back(W);
				rs[prd[v]].push_back(W);
			}
			// 不用判断 prd[u] > prd[v] 的情况
			// 因为这种枚举方式下，一条边 (u, v) 会被作为 (u, v) 和 (v, u) 两次被枚举到
		}
	}

	std :: multiset <int> S;
	std :: memset(ans, 0x3f, sizeof(ans));
	const int inf = ans[0];
	for (int i = 1; i <= k; ++i) {
		for (int d : ls[i])
			S.insert(d);
		if (!S.empty())
			ans[i] = *S.begin();
		for (int d : rs[i])
			S.erase(S.find(d));
	}

	int q = read();
	while (q--) {
		int u = read(), v = read();
		if (u > v)
			std :: swap(u, v);
		int id = eid[u * n + v];
		if (tag[id]) {
			int W = ans[tag[id]];
			if (W == inf)
				puts("Infinity");
			else
				printf("%lld\n", W);
		} else
			printf("%lld\n", dis[t]);
	}

	return 0;
}

CF1163F Indecisive Taxi Fee

与删边最短路不同，这次是改边最短路。

还是先生成 \(T\) 和最短路径 \(P\)，并计算最短路 \(D\)。假设待修改边是 \(e\)，修改前的边权是 \(w(e)\)，修改后的边权是 \(x\)。

明显地，无论怎么改，新图上的最短路就是两种最短路的 \(\min\)：必经 \(e\) 的最短路，以及不经过 \(e\) 的最短路。

【如果 \(\boldsymbol{e \notin E_P}\)】

这种情况是不经过 \(e\) 的最短路更简单：就是 \(D\)。

必经 \(e\) 的最短路其实也挺简单。假设 \(e = (u, v)\)，那么经过 \(e\) 有两种方式：从 \(u\) 进入，从 \(v\) 离开；或者从 \(v\) 进入，从 \(u\) 离开。

因此必经 \(e\) 的最短路是 \(\min(D(1, u) + x + D(v, n), D(1, v) + x + D(u, n))\)。

那么这种情况的总最短路就是 \(\min(D, D(1, u) + x + D(v, n), D(1, v) + x + D(u, n))\)。

必经最短路在 OI 中还是挺常出现的，值得注意。

【如果 \(\boldsymbol{e \in E_P}\)】

这种情况是经过 \(e\) 的最短路更简单：就是 \(D - w(e) + x\)（注意 \(e\) 的边权有修改）。

那不经过 \(e\) 的最短路是什么？删边最短路！于是问题解决。

/*
 * @Author: crab-in-the-northeast 
 * @Date: 2023-04-07 19:01:35 
 * @Last Modified by: crab-in-the-northeast
 * @Last Modified time: 2023-04-07 22:22:22
 */
#include <bits/stdc++.h>
#define int long long
inline int read() {
	int x = 0;
	bool f = true;
	char ch = getchar();
	for (; !isdigit(ch); ch = getchar())
		if (ch == '-')
			f = false;
	for (; isdigit(ch); ch = getchar())
		x = (x << 1) + (x << 3) + ch - '0';
	return f ? x : (~(x - 1));
}

const int maxn = (int)2e5 + 5;
const int maxm = (int)2e5 + 5;
typedef std :: pair <int, int> pii;

std :: vector <pii> G[maxn];
int wei[maxm], us[maxm], vs[maxm], tag[maxm];
int fa[maxn], pred[maxn], dis[maxn], rem[maxn], prd[maxn], ans[maxn];

std :: vector <int> ls[maxn], rs[maxn];

int n, k;

inline int getprd(int u) {
	return prd[u] = (prd[u] == -1 ? getprd(fa[u]) : prd[u]);
}

inline void init() {
	std :: memset(dis, 0x3f, sizeof(dis));
	const int inf = dis[0];
	dis[1] = 0;
	std :: priority_queue <pii> q;
	q.push({0, 1});
	while (!q.empty()) {
		int d = q.top().first, u = q.top().second;
		q.pop();
		if (d + dis[u])
			continue;
		for (pii e : G[u]) {
			int v = e.first, id = e.second, w = wei[id];
			if (dis[v] > dis[u] + w) {
				dis[v] = dis[u] + w;
				fa[v] = u;
				pred[v] = id;
				q.push({-dis[v], v});
			}
		}
	}

	std :: vector <int> P;
	for (int u = n; u; u = fa[u])
		P.push_back(u);
	std :: reverse(P.begin(), P.end());
	k = (int)P.size() - 1;
	std :: memset(prd, -1, sizeof(prd));
	for (int i = 0; i <= k; ++i) {
		prd[P[i]] = i;
		tag[pred[P[i]]] = i;
	}
	for (int u = 1; u <= n; ++u)
		if (dis[u] < inf)
			getprd(u);
	
	std :: memset(rem, 0x3f, sizeof(rem));
	rem[n] = 0;
	q.push({0, n});
	while (!q.empty()) {
		int d = q.top().first, u = q.top().second;
		q.pop();
		if (d + rem[u])
			continue;
		for (pii e : G[u]) {
			int v = e.first, id = e.second, w = wei[id];
			if (rem[v] > rem[u] + w) {
				rem[v] = rem[u] + w;
				q.push({-rem[v], v});
			}
		}
	}
	return ;
}

signed main() {
	n = read();
	int m = read(), q = read();
	for (int i = 1; i <= m; ++i) {
		int u = us[i] = read(), v = vs[i] = read(), w = read();
		G[u].push_back({v, i});
		G[v].push_back({u, i});
		wei[i] = w;
	}

	init();

	for (int i = 1; i <= m; ++i) {
		int u = us[i], v = vs[i], w = wei[i];
		if (tag[i] || prd[u] == prd[v])
			continue;
		if (prd[u] > prd[v])
			std :: swap(u, v);
		int W = dis[u] + w + rem[v];
		ls[prd[u] + 1].push_back(W);
		rs[prd[v]].push_back(W);
	}

	std :: multiset <int> S;
	std :: memset(ans, 0x3f, sizeof(ans));
	for (int i = 1; i <= k; ++i) {
		for (int d : ls[i])
			S.insert(d);
		if (!S.empty())
			ans[i] = *S.begin();
		for (int d : rs[i])
			S.erase(S.find(d));
	}

	while (q--) {
		int t = read(), x = read(), u = us[t], v = vs[t], w = wei[t];
		printf("%lld\n", tag[t] ? 
			std :: min(ans[tag[t]], dis[n] - w + x) : 
			std :: min({dis[n], dis[u] + x + rem[v], dis[v] + x + rem[u]}));
	}

	return 0;
}

有向图（疑似无靠谱做法）

由于无向图的 \(\mathbf{Lemma\ 4}\) 引理无法推广到有向图上，所以无向图的做法无法移植到有向图。

目前学术界似乎还没有最坏复杂度优于暴力的做法。

另外，P3238 是个有向图删边最短路模板，然而目前还没有正确性和复杂度都有保障的解法。

hack1

这个 hack 针对无向图做法直接移植到有向图，属于 hack 正确性。

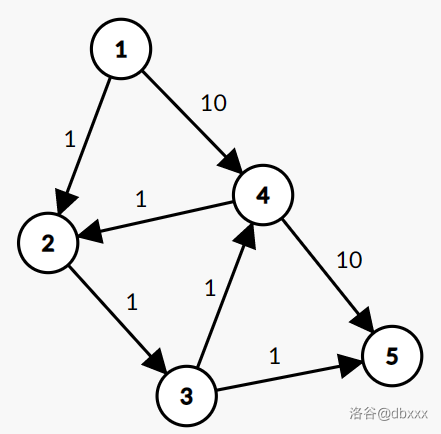
原最短路为 \(1 \to 2 \to 3 \to 5\)。

考虑删去 \(2 \to 3\) 后，删边最短路会变为 \(1 \to 4 \to 5\)。

不难发现，在原图上，\(1 \rightsquigarrow 4\) 的最短路不是 \(1 \to 4\) 而是 \(1 \to 2 \to 3 \to 4\)，\(4 \rightsquigarrow 5\) 的最短路不是 \(4 \to 5\) 而是 \(4 \to 2 \to 3 \to 5\)。

因此类似无向图上“一个删边最短路，一定对应着原图上强制经过某一条非最短路边后的最短路”的结论不再成立。

如果无向图做法移植到有向图，会误判删掉 \(2 \to 3\) 后，没有新最短路。

hack2

这个 hack 针对 SPFA 乱搞，属于 hack 时间复杂度。

下面给出 generator。

#include <bits/stdc++.h>

const int N = 20000, M = 4 * N - 1, L = N;

int main() {
    printf("%d %d %d\n", N * 2 + 1, M, L);
    for (int i = 1; i < N; ++i) printf("%d %d %d\n", i, i + 1, 1);
    printf("%d %d %d\n", N, N * 2 + 1, 1);
    for (int i = 1; i <= N; ++i) printf("%d %d %d\n", i, i + N, N - i + 1);
    for (int i = 1; i <= N; ++i) printf("%d %d %d\n", i + N, i, 1);
    for (int i = 1; i < N; ++i) printf("%d %d %d\n", i + N, i + N + 1, 1);
    for(int i = 1; i <= L; ++i) printf("%d ", i); puts("");
    return 0;
}

事实上上面的 \(N\) 调成 \(5000\) 就足以 hack 掉 P3238 所有 SPFA 乱搞做法。

关于卡 SPFA 就不过多解释了，和本文没啥关系。

tips

有考虑过暴力吗？

明显地，我们只需要考察某条最短路上的边的删边最短路。但是注意到，最短路的边数不仅不会超过 \(m\)，而且不会超过 \(n - 1\)。

因此如果 \(n\) 比较小而 \(m\) 比较大，我们只需要做 \(n - 1\) 次 dijkstra 而不是 \(m\) 次。

上面的性质告诉我们，影响 \(1 \rightsquigarrow n\) 最短路的边不会超过 \(n - 1\) 条。

事实上有更强的性质：影响单源最短路的边不会超过 \(n - 1\) 条（这里就假设源点为 \(1\) 吧）。

也就是说，如果删除 \(e\) 之后，只要存在一个 \(u\)，\(1 \rightsquigarrow u\) 的最短路有变，那么就称 \(e\) 是有影响的；那么有影响的边不超过 \(n - 1\) 条。

为什么？考虑构建以 \(1\) 为根的任意一棵最短路树，最短路树上总共只有 \(n - 1\) 条边。

最短路树上的边可能有影响，也可能没影响（毕竟最短路树只包含 \(1 \rightsquigarrow u\) 的一条最短路径，删了之后可能还有别的最短路径）。

但是，不在最短路树上的边一定是没影响的。所以有影响的边不超过 \(n - 1\) 条。

于是你就会做 P6880 了。这题的原理就是 \(n\) 比较小，所以考察删边最短路只需要暴力 \(n\) 次 dijkstra。

有向无权图

论文科技，非确定性算法，线性根号对数，有兴趣的可以点下面的文章了解：

https://www.cnblogs.com/Elegia/p/16461398.html

最后

如果觉得这篇文章写得好，请不要忘记给个赞！

标签：prd,int,短路,路径,rightsquigarrow,笔记,删边,mathrm
From： https://www.cnblogs.com/crab-in-the-northeast/p/remove-edge-shortest-path.html

删边最短路学习笔记