卡特兰数
问题
给定 \(n\) 个 \(0\) 和 \(n\) 个 \(1\),它们将按照某种顺序排成长度为 \(2n\) 的序列,它们能排列成的所有序列中,能够满足任意前缀序列中 \(0\) 的个数都不少于 \(1\) 的个数的序列有多少个?
转化
我们将上面的问题进行转化:

问:从 \((0, 0)\) 点走到 \((n, n)\) 点,且只能向右或向上走,共有多少种方案?
如果向右走一格,记为 \(0\),如果向上走一格,记为 \(1\)。因此,每一条路径都对应一个 \(01\) 序列。
将这个问题进行转化后,我们还需要增加一个条件 : 保证在任意时刻,满足 \(x \ge y\)。
所以,我们对这个问题进行更严谨的描述:
从 \((0, 0)\) 点走到 \((n, n)\) 点,且只能向右或向上走,且在任意时刻,满足 \(x \ge y\),共有多少种方案?
将问题转化后,我们得到了一个与原题不同,但结果一致的问题。
由于每个时刻点的坐标要保证 \(x \ge y\),所以我们可以进一步的分析:
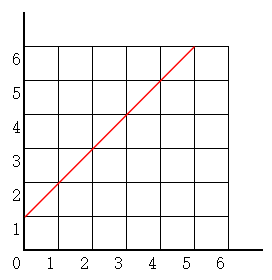
在任意时刻,所走过的路径不得碰到红线。
求解
对于这个问题,可以反过来思考,也就是求出经过红线的路径数量,再用总方案数减掉这些路径。
总方案数
从 \((0, 0)\) 点走到 \((n, n)\) 点,只能向右或向上走,也就是一共要向右走 \(n\) 步,向上走 \(n\) 步,一共要走 \(2n\) 步。其中向上走的 \(n\) 步可以在 \(2n\) 步中任意走。所以从 \((0, 0)\) 点走到 \((n, n)\) 点,只能向右或向上走的总方案数就是 \(C_{2n}^n\)。
经过红线的方案数
假如走过的路径如下图:

图中第一次碰到红线的点是 \((3, 4)\),那么将 \((3, 4)\)后面的点对于红线做轴对称,即:

那么此时的终点从 \((6, 6)\) 变到了 \((5, 7)\)。
也就是说,从 \((0, 0)\) 点走到 \((6, 6)\) 点,只能向右或向上走,且碰到红线的方案数 等于 从 \((0, 0)\) 点走到 \((5, 7)\) 点的总方案数。
根据上面从 \((0, 0)\) 到 \((n, n)\) 的推导,从 \((0, 0)\) 到 \((5, 7)\) 的方案数即 \(C_{5+7}^7\),带入字母也就是 \(C_{(n-1) + (n+1)}{n+1}\),化简即 \(C_{2n}^{n+1}\)。
结论
至此,总方案数和经过红线的方案数都推导完毕,那么最开始的问题也就是
\[C_{2n}^{n} - C_{2n}^{n+1} \]对其进行化简:
\(\ \ \ C_{2n}^{n} - C_{2n}^{n+1}\)
\(= \dfrac{(2n)!}{(n!)\cdot (n!)} - \dfrac{(2n!)}{(n-1)! \cdot (n + 1) !}\)
\(= \dfrac{(2n)! \cdot (n+1) - (2n)! \cdot n}{(n+1)! \cdot n}\)
\(= \dfrac{(2n)!}{(n+1)!\cdot (n!)}\)
\(= \dfrac{1}{n+1} \cdot \dfrac{(2n)!}{(n!)\cdot (n!)}\)
\(= \dfrac{C_{2n}^n}{n+1}\)
代码
int C(int n, int m){
int res = 1;
for(int i=n; i>n-m; i--){
res = mul(res, i);
}
for(int i=1; i<=m; i++){
res = mul(res, fpm(i, mod - 2));
}
return res;
}
int catalan(int n){
return mul(C(2*n, n), fpm(n + 1, mod - 2));
}