二项式反演
我们直接上式子好了
一般有两种形式,第一种是
\[f(n)=\sum_{i=0}^n\binom{n}{i}g(i)\iff g(n)=\sum_{i=0}^n(-1)^{n-i}\binom{n}{i}f(i) \]第二种是
\[f(n)=\sum_{i=n}^m\binom{i}{n}g(i)\iff g(n)=\sum_{i=n}^m\binom{i}{n}(-1)^{i-n}f(i) \]第二种比第一种更加常用。
一般来说我们的 \(f(n)\) 是钦定 \(n\) 个元素必须选中,剩下的随便选的方案数。注意 \(f\) 并非单纯的后缀和。
例题
球的染色
有 \(n\) 个球排成一列,每个球可以染成 \(m\) 种颜色,相邻球的颜色不能相同,但是每种颜色至少出现一次,问方案数。
如果没有至少出现一次的限制那么答案就是 \(m\times (m-1)^{n-1}\)。
考虑转化为 恰好有 \(0\) 个颜色没有出现过,那么设 \(f(k)\) 为钦定某 \(k\) 种颜色没有出现的方案数,那么 \(f(k)=(m-k)\times (m-k-1)^{n-1}\)。
设 \(g(k)\) 为恰好 \(k\) 个颜色没有出现过的方案数,那么
\[f(k)=\sum_{i=k}^m\binom{i}{k}g(i)\iff g(k)=\sum_{i=k}^m(-1)^{i-k}\binom{i}{k}f(i)=\sum_{i=k}^m(-1)^{i-k}\binom{i}{k}(m-k)\times (m-k-1)^{n-1} \]那么 \(g(0)\) 就是答案啦
SDOI2016 排列计数
考虑设 \(f(x)\) 为钦定 \(x\) 个位置必须放对,剩下的随便放,那么 \(f(x)=\binom{n}{x}(n-x)!=\frac{n!}{x!}\)。
乘上 \(\binom{n}{x}\) 的原因是我们要先选出来这 \(x\) 个位置。然后 \(g(x)\) 表示恰好放对 \(x\) 个位置的方案数,我们有
\[f(x)=\sum_{i=x}^n\binom{i}{x}g(i)\iff g(x)=\sum_{i=x}^n\binom{i}{x}(-1)^{i-x}f(i) \]然后你用 \(f(x)=\frac{n!}{x!}\) 化简一下发现
\[g(x)=\sum_{i=x}^n\dfrac{i!}{x!(i-x)!}(-1)^{i-x}\times\dfrac{n!}{i!}=\sum_{i=x}^n\dfrac{n!}{x!(n-x)!}\times (-1)^{i-x}\dfrac{(n-x)!}{(i-x)!}=\binom{n}{x}(n-x)!\sum_{i=0}^{n-x}\dfrac{(-1)^i}{i!} \]前后都可以 \(O(n)\) 预处理,于是这题就做完了。AC Code
BZOJ2839 集合计数
先选出 \(x\) 个元素必须在交集里面,那么剩下的 \(n-x\) 个元素可以构成 \(2^{n-x}\) 个集合,可以随便选但不能一个都不选,因此方案数为
\[f(x)=\binom{n}{x}\left(2^{2^{n-x}}-1\right) \]然后设 \(g(x)\) 为交集大小恰好为 \(k\) 的方案数,那么
\[f(x)=\sum_{i=x}^n\binom{i}{x}g(i)\iff g(x)=\sum_{i=x}^n(-1)^{i-x}\binom{i}{x}f(i) \]注意到只有一次询问,因此可以先算出来 \(f\) 然后直接算出来 \(g\)。不难在 \(O(N)\) 时间内解决。AC Code
BZOJ3622 已经没有什么好害怕的了
记糖果为 \(A_{1\cdots n}\),药片为 \(B_{1\cdots n}\)。那么当 \(n,k\) 不同奇偶时无解,否则应当有 \(\frac{n+k}{2}\) 个位置满足 \(A_i>B_i\),剩下的为 \(A_i<B_i\)。
下面记 \(k\) 为原来的 \(\frac{n+k}{2}\)。 仍然是钦定 \(k\) 个位置,让这 \(k\) 个位置满足 \(A_i>B_i\),想想怎么算方案数。发现不是很好用组合数算。
对于每个 \(A_i\) 我们算出来 \(C_i\) 表示 \(B\) 中 \(<A_i\) 的元素个数,将 \(A\) 从小到大排序,那么 \(C\) 序列递增且前面的 \(C\) 是后面的子集。
现在相当于要钦定 \(k\) 个位置选出 \(C_i\) 所代表的集合中的数且不能重复,剩下的随便选。
这个可以 DP 做,\(f(i,j)\) 表示前 \(i\) 个数配了 \(j\) 组时的方案数,那么 \(f(i,j)=f(i-1,j)+f(i-1,j-1)\times (C_j-(j-1))\)。
那么记 \(F_j=(n-j)!f(n,j)\),答案就是 \(F\) 做一个二项式反演。于是这题就做完了,时间复杂度 \(O(n^2)\)。AC Code
JSOI2011 分特产
设 \(f(k)\) 为钦定 \(k\) 个人,他们分不到特产,剩下的人随便分,的方案数。那么答案就是 \(f\) 做一个二项式反演。
注意到 \(f(k)\) 实际上等价于给 \(n-k\) 个人分特产,不过可以有人没分到的方案数。
然后我们发现其实每种特产大概是独立的,那么给 \(m\) 个人分的时候答案就是
\[\prod_{i=1}^n\binom{a_i+m-1}{m-1} \]我们对每个 \(m\) 把这东西算一遍就得到了 \(f\),再反演就得到了 \(g\)。暴力算是 \(O(n^2)\) 的,已经可以通过。AC Code
实际上我们拆拆式子发现
\[\prod_{i=1}^n\binom{a_i+m-1}{m-1}=\prod_{i=1}^n\dfrac{(a_i+m-1)!}{a_i!(m-1)!}=\prod_{i=1}^n\dfrac{(a_i+m-2)!}{a_i!}\prod_{i=1}^n(a_i+m-1)\times \dfrac{1}{((m-1)!)^n} \]我们发现只要能快速算出来 \(\prod (a_i+m-1)\) 就能递推。
设 \(F(x)=\prod(a_i+x)\),那么可以分治 NTT 在 \(O(n\log ^2n)\) 的时间内得到 \(F\),再 \(O(n\log ^2n)\) 做个多点求值,就得到了 \(O(n\log ^2n)\) 的算法。
NOI Online#2 提高组 游戏
和 BZOJ3622 比较相似,考虑钦定 \(k\) 个位置,让这 \(k\) 个位置不是平局。我们将 A 的点染黑,B 的点染白。
现在相当于要选出 \(k\) 组互为祖孙关系的点对,求方案数。
这个可以用树形 DP 做,设 \(f(u,j)\) 为只考虑点 \(u\) 子树内的点,配 \(j\) 对的方案。
设 \(X_u\) 为 \(u\) 子树中白点个数,\(Y_u\) 为 \(u\) 子树中黑点个数,转移时考虑看 \(u\) 是否配对:
- 如果 \(u\) 不配对,那么直接把 \(u\) 的儿子的背包合并上来即可。
- 如果 \(u\) 配对,不妨设 \(u\) 是黑点,此时相当于子树中已经配了 \(j-1\) 对,那么 \(u\) 还有 \(X_u-(j-1)\) 种选择。因此将子树内 \(j-1\) 的背包合并上来再乘 \((X_u-(j-1))\) 即可。
那么我们可以 \(O(n^2)\) 算出来钦定 \(k\) 个位置的方案数,再 \(O(n^2)\) 反演一遍就完事了。AC Code
JSOI2015 染色问题
我们发现这题有三个限制。如果没有限制,那么答案就是 \((C+1)^{n\times m}\)。
考虑设 \(f(i,j,k)\) 为钦定某 \(i\) 行,某 \(j\) 列全都空着,某 \(k\) 种颜色不选的方案数,那么 \(f(i,j,k)=(C-k+1)^{(n-i)\times (m-j)}\binom{n}{i}\binom{m}{j}\binom{C}{k}\)。
然后设 \(g(i,j,k)\) 为恰好 \(i\) 行 \(j\) 列 \(k\) 种颜色不选的方案数,有
\[f(i,j,k)=\sum_{x=i}^n\sum_{y=j}^m\sum_{z=k}^C\binom{x}{i}\binom{y}{j}\binom{z}{k}g(i,j,k) \]发现是个三维的二项式反演,我们猜想
\[g(i,j,k)=\sum_{x=i}^n\sum_{y=j}^m\sum_{z=k}^C(-1)^{x+y+z-i-j-k}\binom{x}{i}\binom{y}{j}\binom{z}{k}f(i,j,k) \]从容斥的角度考虑一下,感觉很对。直接做要带个 \(\log\),不过不难做到 \(O(n^3)\)。AC Code
注意到其实三维中有一维可以直接算出来,所以不难优化到 \(O(n^2)\)。。。(我是傻子qaq
ABC266G Yet Another RGB Sequence
考虑钦定 \(i\) 个位置是 RG,那么还剩 \(R-i\) 个 R,\(G-i\) 个 G,\(B\) 个 B,方案数可以随便算。
于是就做完了,果然是板子题。
ABC217G Groups
我们考虑对非空这个条件做容斥。
具体来说把 \(1,2,\cdots N\) 分成 \(M\) 组,第 \(i\) 组中每个数都 \(\bmod M=i\),设其大小为 \(C_i\)。
现在我们钦定其中某 \(i\) 组是空的,那么
\[f(i)=\prod_{j=0}^{M-1}\binom{k-i}{C_j}\times C_j! \]那么答案可以直接通过二项式反演 \(O(M)\) 得到。
我们发现如果直接算的话需要算 \(N\) 次,每次都要 \(O(NM)\),过不去。
但是可以发现本质不同的 \(k-i\) 其实只有 \(O(N)\) 组,因此直接处理出来所有的
\[F_x=\prod_{j=0}^{M-1}\binom{x}{C_j}\times C_j! \]然后算 \(f(i)\) 就只需要查表了。总的复杂度为 \(O(NM)\)。AC Code
CF285E Positions in Permutation
设 \(f(i,j,0/1,0/1)\) 表示由 \(1\cdots i\) 构成的排列,有 \(j\) 个 good position 的方案数,后面两个 \(0/1\) 的含义待会再说。
我们考虑这样由 \(1,2,\cdots,i\) 的排列构建一个 \(1,2,\cdots,i+1\) 的排列:先把最后一位放上 \(i+1\),再将最后一位和前面的某一位 swap 一下。
这样一来,我们只需要分别计算出来有多少种 swap 可以使得 good position 的数量 \(+1/-1/\) 不变即可。
我们考虑 \(x\) 满足 \(a_x=i\) 以及 \(a_i\) 的值是什么。进行一个分类:
- 如果 \(i+1\) 和某个 \(x,i\) 之外的数 swap 了, 那么如果原本那个位置是 good position,\(j\) 需要减一;否则不变。
- 如果和 \(x\) 进行 swap,那么 \(i+1\) 会是一个 good position,但是 \(x\) 那个位置原本是不是 good position 我们不知道,因此需要记录一下。
- 如果和 \(i\) 进行 swap,那么 \(i\) 会是一个 good position,但是这个位置原本是不是 good position 我们也不知道,需要记录一下。
因此状态就是:
- \(f(i,j,0/1,0/1)\) 表示由 \(1\cdots i\) 构成的排列,有 \(j\) 个 good position,第 \(i\) 个位置是不是 \(i-1\),第 \(i-1\) 个位置是不是 \(i\),的方案数。
转移分类讨论一下就行了。等等说好的二项式反演在哪里呢
我们思考一下容斥做法:直接钦定某 \(k\) 个位置为 good position,剩下的位置的方案数我们默认为 \(1\)。
我们发现这个东西类似于一个匹配:
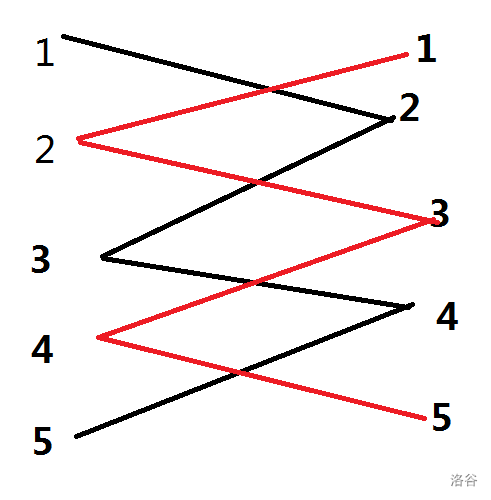
我们把黑边拉直,然后相当于要从 \(n-1\) 条边中选出 \(k\) 条互不相邻的边。简单插板得到 \(f(k)=\binom{n-k}{k}\)。
那么我们的 \(F\) 就是 \(f\) 和自己卷一下,答案就是
\[G(m)=\sum_{i=m}^n(-1)^{i-m}F(k) \]暴力 \(O(n^2)\) 计算已经可以通过本题。注意到 \(F\) 是个卷积,因此可以做到 \(O(n\log n)\)。
CF997C Sky Full of Stars
相信做了之前那么多题之后这题已经非常简单了。。。
考虑钦定某 \(k\) 列是同一种颜色,剩下的随便填,并且需要满足每一行都不是同一种颜色。有
\[f(k)=\begin{cases}(3^n-3)^n&,k=0\\\binom{n}{k}\times\left(3\times \left(3^{n-k}-1\right)^n+\left(3^k-3\right)\times 3^{n(n-k)}\right)&,k>0\end{cases} \]然后二项式反演再做个小容斥就完事了。时间复杂度 \(O(n\log n)\) 或 \(O(n)\)。AC Code
CF995F Cowmpany Cowmpensation
这题有个拉格朗日插值的做法,不过我们可以用容斥过掉它。
我们发现虽然值域很大,但是实际上用到的数只可能有 \(O(n)\) 种。
设 \(g(i)\) 为恰好用 \([1,i]\) 中每个数填好,并且每种数至少出现一次,的方案数,那么答案就是 \(\sum_{x}\binom{D}{x}g(x)\)。
这是因为我们可以把一种方案离散化掉,那么离散化到 \([1,x]\) 的方案数恰为 \(\binom{D}{x}\)。
我们发现至少出现一次看着就很容斥,因此可以求出来 \(f(i)\) 表示只用 \([1,i]\) 中的数,随便填(可以有某些数没有用到)的方案数。
那么 \(g\) 其实就是 \(f\) 二项式反演一下,于是就可以 \(O(n^2)\) 直接算了。代码懒得写了,,先坑着
标签:方案,那么,技巧,sum,容斥,times,反演,binom From: https://www.cnblogs.com/YunQianQwQ/p/16712137.html