3.19 小记

有一个问题是我最近做题效率超级超级差。

先写一写以前做过的题吧。

CF923E Perpetual Subtraction

懒得打公式捏。

收录到各种多项式和生成函数科技题里面了

P4005 小 Y 和地铁

爆搜，爆搜和爆搜。

首先确定的是爆搜有 \(8\) 种情况，如图。

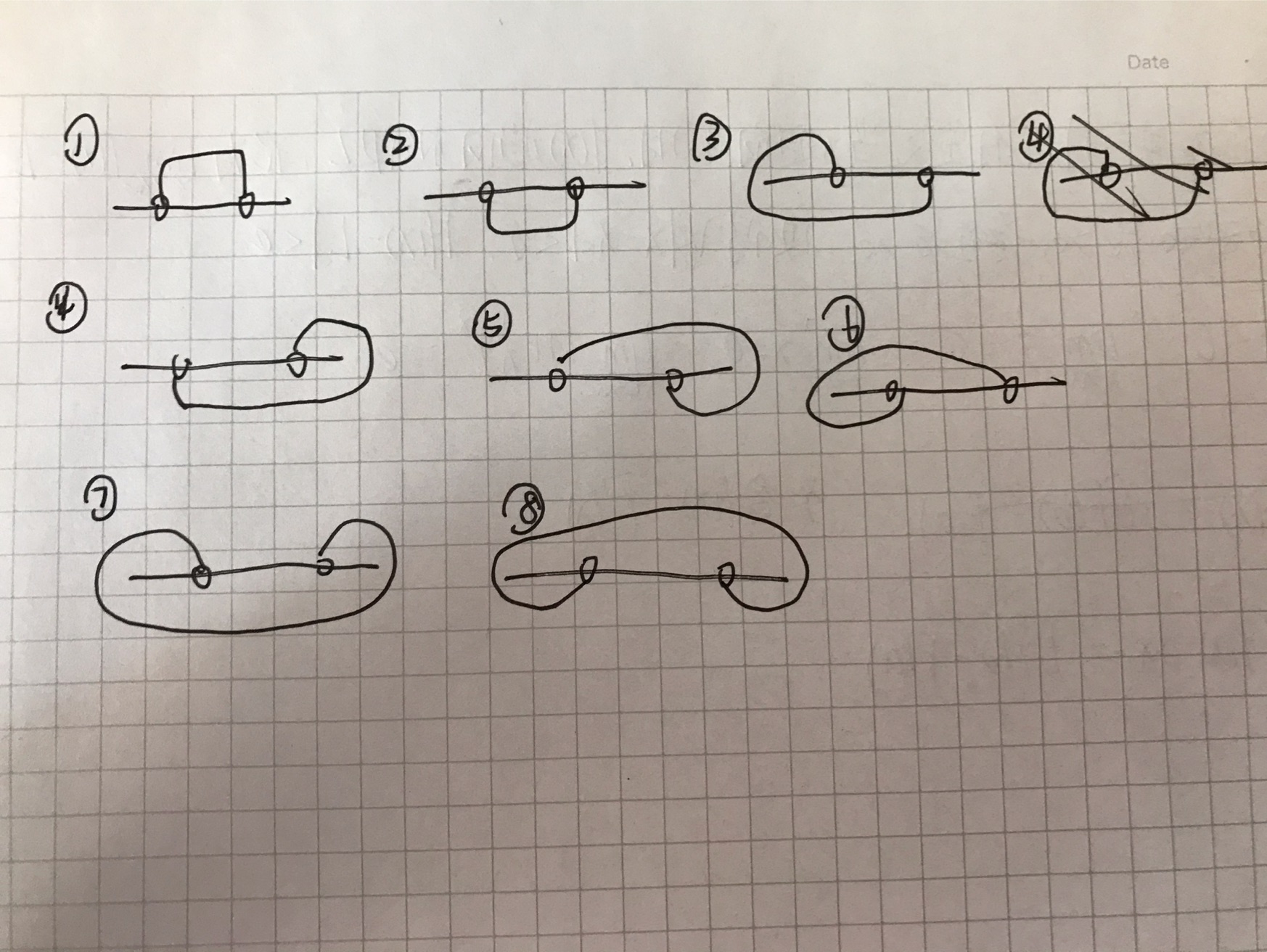
然后是可以分析得到，如果两条路线正好把上下两侧全覆盖了，那么另外一条路线要么和红线交，要么和黑线交，所以搜的时候只搜索红线就够了。

这样 \(3,6,7,8\) 是无用的，扔掉。现在枚举的复杂度是 \(O(n4^{n})\)，乘 \(n\) 是验证的复杂度。

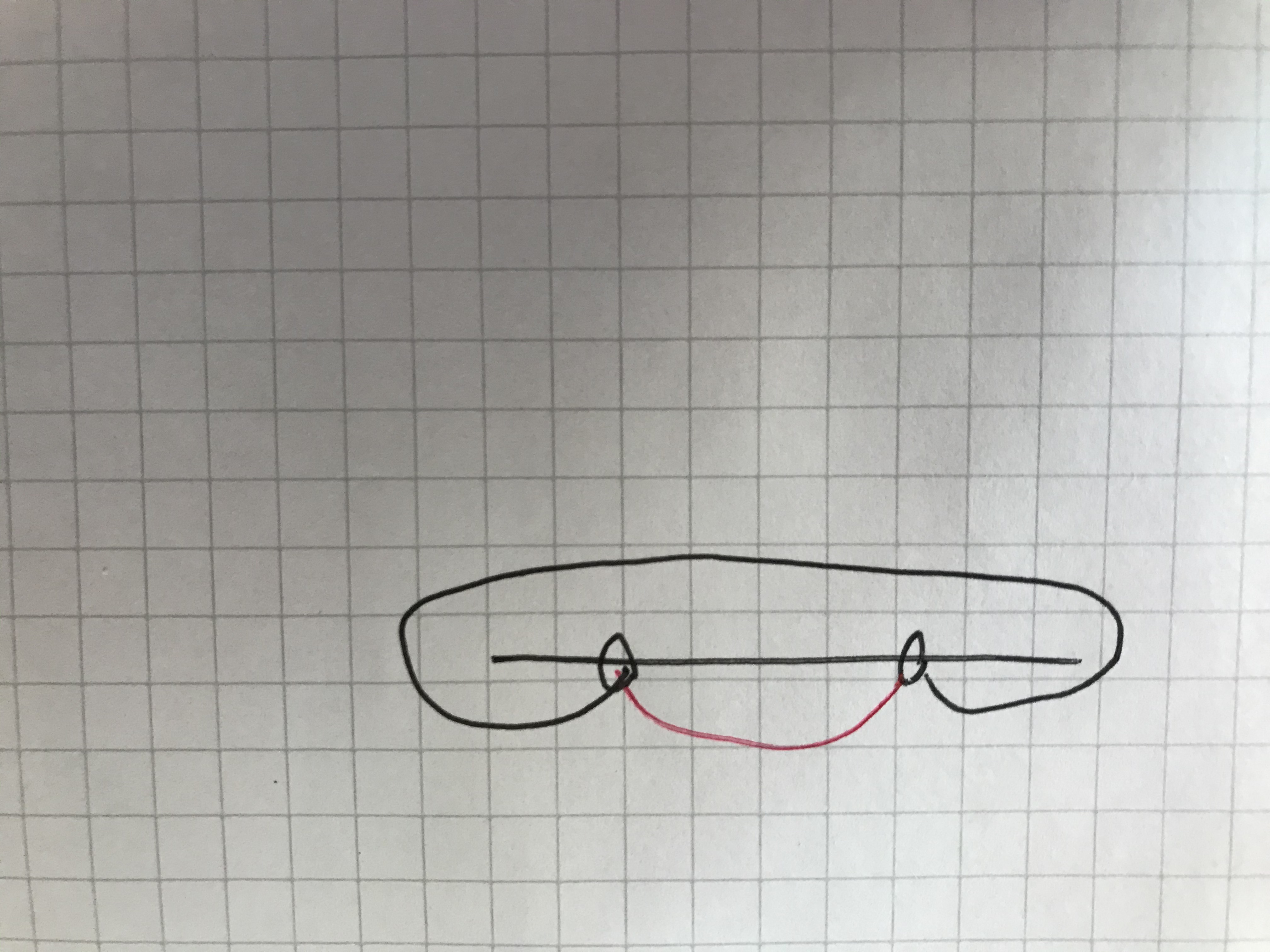
然后我们发现，如果我们是按照左端点从左到右枚举的，那么这两种情况下，在之后的枚举中，和上面一样，其他线路要么都不交，要么都相交，所以只需要算出两种线路哪种在前面产生的贡献更小，然后选小的那个就行。

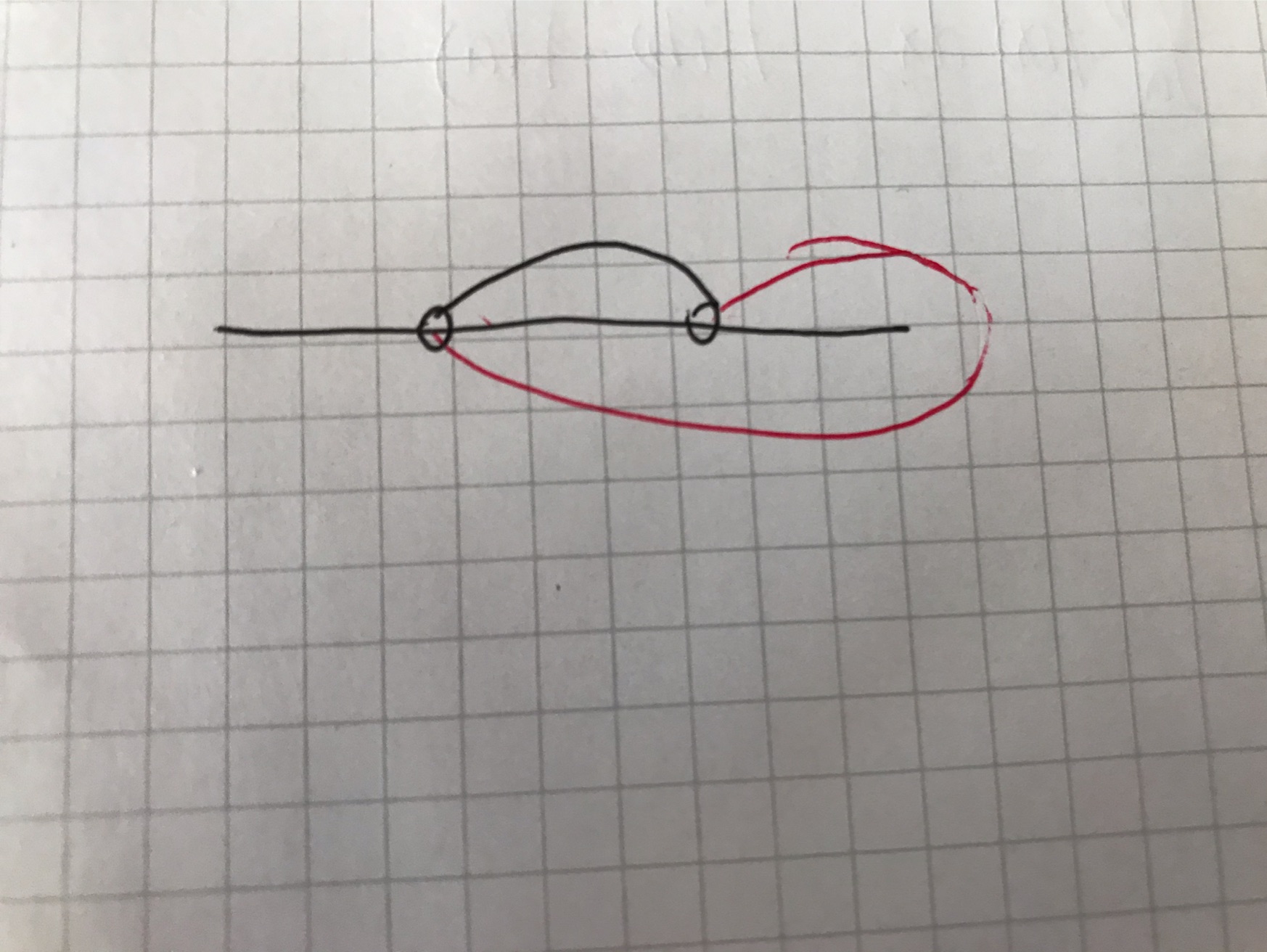
如果每次都 \(O(n)\) 的算一遍交点还是太麻烦。由于我们是按左端点排序，所以我们用树状数组维护右端点的位置的数量，后面的线段查交点时只要线段覆盖的位置数量的和即可。

P6105 [Ynoi2010] y-fast trie

首先插进来的数字都 \(\mod C\) 是没毛病的。

然后有两种情况就是。

一种是两个数加起来小于 \(C\) 但接近 \(C\) 。

另一种是加起来大于 \(C\) 并且很大。

第二种情况是好办的，因为只需要找到两个最大的就行。毕竟两数之和不可能大于 \(2C\)。

第一种情况是不好的。因为对每个数都找到合适的匹配的话是 \(O(n^2\log n)\) 的。

但是有一个结论，如果 \(x\) 的最佳匹配是 \(y\) ，\(y\) 的最佳匹配是 \(z\)，那么 \(x+y<y+z(x\not = z)\)

看着很智障的结论。

有了这个性质之后，我们发现 \(x\) 是不可能贡献到答案里的。那么只需要维护双向选择的数对即可。我们可以开两个 set，这样一个维护数集，另外一个维护选择之后的对即可。

P8512 [Ynoi Easy Round 2021] TEST_152

首先区间推平。珂朵莉树。

然后考虑怎么统计答案。我们先考虑离线询问，从左到右加操作。与此同时在以时间轴建立的线段树上维护总和。就是珂朵莉树会把区间分段。加入的时候就加上区间长度乘权值这么多，删除就是减掉。这样线段树维护单点修改，区间查询即可。

[ABC276Ex] Construct a Matrix

神秘神秘。

矩阵中只存在 \(0,1,2\)。

如果要求一个矩阵全是 \(0\) 就好办了。直接有一个 \(0\) 就行。如果要求是 \(1\) 或 \(2\) 的话就不能有 \(0\) 。

我们通过手玩可以发现：\(1\) 的填入不会改变模 \(3\) 的乘积，但是每加入一个 \(2\) 都会改变。我们维护每个点的二维前缀 \(2\) 的数量的奇偶性。然后就转化为了异或方程组。具体解法就高斯消元。然后判断一下每个点比不必要放东西，以及放什么。如果发现异或方程组无解或最后发现 \(0\) 的矩形里面一个 \(0\) 都放不进去，就不行。否则就行。

#loj6289. 花朵

我做过一个跟这个几乎一模一样的题，但是还是写了好长时间/kk

菊花的转移我觉得我挺明白的，不过链上的当时也没想明白。

这个呢就是每个点有两个方程 \(F[i][j],G[i][j]\)，一个表示自己没选，另一个表示自己选了。然后用矩阵转移的话需要考虑头尾分别是什么

这样比较好理解了。

还有点细节就是分治 NTT 时不要带着个 stl 的大数组下传进去，（复杂度好像会假）

#loj6672. 「XXOI 2019」惠和惠惠和惠惠惠

强调一下最后一次必为 \(0\)。题面有误

这种数居然有名字？
首先就是 \(f_{i,j}\) 表示前 \(i\) 个回合，正好 \(j\) 次正好为 \(0\)

\(f_{i,j}=\sum\limits_{k=0}^{i-1} f_{k,j-1}h(i-k)\) \(h(i)\) 表示走了 \(i\) 步，只有头和尾正好碰到 \(0\) 的方案数。只要知道了 \(h(i)\) 那只要乘 \(k\) 次即可。

现在考虑怎么求 \(h(i)\) 我们先固定第一步和最后一步，剩下的就可以随便碰到 \(0\) 了，这样我们求出来后需要右移 \(2\) 位。

那么 \(h(i) =\sum \limits_{j=0}^i \dbinom i j D(i-j)\) 意思就是选出来 \(j\) 步走 \(0\)，\(D(i)\) 是卡特兰数。

这样就求完了。巨大卡常很烦人。

[ABC277Ex] Constrained Sums

每次我对 \(2-SAT\) 好像都有新的理解。

首先我觉得是个有用的套路：如果 \(l\leq a+b\leq r\) ，那么对于任意 \(t\)，要么 \(t\leq a\)，要么 \(t>L-b\)。要么 \(t>b\) ，要么 \(t\leq R-a\)。

证明：如果 \(t>a\) 且 \(t\leq L-b\) ，那么 \(a<L-b\)， \(a+b<L\) 矛盾，所以不行。那么当 \(t>a\) 时，\(t>L-b\)。

同理如果 \(t>L-b\) 且 \(t\leq a\) 时也矛盾，所以要么 \(t\leq a\)，要么 \(t>L-b\)。

这种要么，要么的关系，然后就可以 2-SAT 了。

我理解上 2-SAT 的连边就是一个如果成立，连向的边必须成立。所以一个强联通分量里要么全成立要么全不成立。如果矛盾且必有一个的一堆在同一个强联通分量里，那么必然矛盾。然后如果拓扑序越大的，说明应当先选这个，而不是选小的。因为选小的有可能造成大的跟着一起选了。

废话

这篇文章的原标题是 3.18 小记。由于我太懒了所以拖到了今天。

昨天会考。跟红太阳一个考场。考完数学的时候红太阳的第一句话是“导数不是选修内容吗，怎么会考还考”，给我整不会了。然后意识到红太阳用导数秒掉了一堆证明单调性的水题。

我又意识到我导数的水平已经倒退回到道听途说的级别。所以今天上午学了一点，但是就是一点。

然后下午有点困。