前言
树状数组作为维护序列区间修改与查询的利器
是每一个 “OIer” 都应该要掌握的知识点
今天，我们来详细的整理一下树状数组的知识脉络
目录
一.树状数组简介
二.树状数组的实现
1.单点修改+区间查询
2.区间修改+单点查询
3.区间修改+区间查询
三.树状数组的应用
1.求逆序对
2.树状数组倍增
四.二维树状数组
正文
树状数组简介
树状数组即形如下图的树形结构：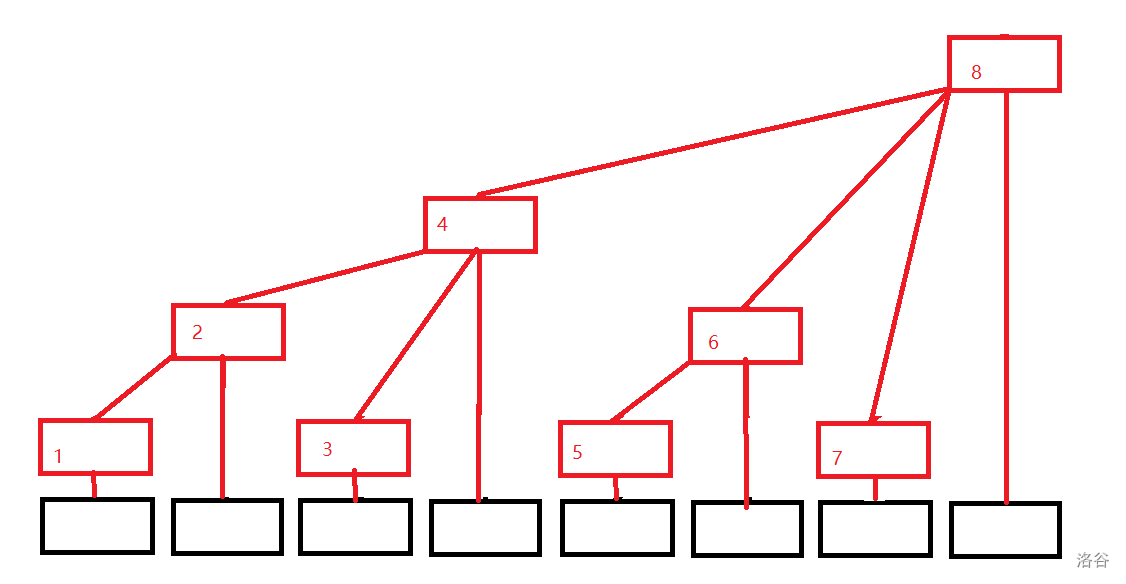 
其基本性质为tree[i]=a[i-2^k+1]+a[i-2^k+2]+...+a[i]tree[i]=a[i−2k+1]+a[i−2k+2]+...+a[i]其中kk为ii的二进制中从最低位到高位连续零的长度；treetree表示树状数组；aa表示原数组
我们可以使用 lowbit 来找到最低位的0lowbit(x)=x\&(-x)lowbit(x)=x&(−x)
树状数组的实现
首先我们要明白，树状数组的本质依然是在维护数列中的某一个数的加减和对于数列前缀的求和，除此之外不能够进行其他的任何操作
因此我们需要合理的运用其他思想来利用树状数组解决问题
1.这里是实现对数列中的某一个数的加减的实现
void add(int x,int y)
{
for(int i=x;i<=n;i+=lowbit(i))
tree[i]+=y;
return;
}2.这里是对求区间前缀和的实现
int get(int x)
{
int sum=0;
for(int i=x;i>=1;i-=lowbit(i))
{
sum+=tree[i];
}
return sum;
}单点修改+区间查询
关于单点修改+区间查询，我们很容易想到运用前缀和求解，这种方法完全贴合树状数组的基本操作，因而就不过多追述了
模板：【模板】树状数组 1
代码：
#include<bits/stdc++.h>
using namespace std;
int n,m;
int a[500001];
int tree[500001];
int lowbit(int x)
{
return x&(-x);
}
void add(int x,int y)
{
for(int i=x;i<=n;i+=lowbit(i))
tree[i]+=y;
return;
}
int get(int x)
{
int sum=0;
for(int i=x;i>=1;i-=lowbit(i))
{
sum+=tree[i];
}
return sum;
}
int main()
{
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++)
{
scanf("%d",&a[i]);
add(i,a[i]);
}
for(int i=1;i<=m;i++)
{
int op,l,r;
scanf("%d%d%d",&op,&l,&r);
if(op==2)
printf("%d\n",get(r)-get(l-1));
else
add(l,r);
}
return 0;
} 区间修改+单点查询
实现区间修改+单点查询的方法同样好想，我们很容易由前缀和想到差分求解，因为树状数组的查询是求前缀和，因此刚好我们就可以还原出单个元素的值
模板：【模板】树状数组 2
代码：
#include<bits/stdc++.h>
using namespace std;
int n,m;
int a[500005];
int tree[500005];
int lowbit(int x)
{
return x&(-x);
}
void add(int x,int y)
{
for(int i=x;i<=n;i+=lowbit(i))
tree[i]+=y;
return;
}
int get(int x)
{
int sum=0;
for(int i=x;i>=1;i-=lowbit(i))
{
sum+=tree[i];
}
return sum;
}
int main()
{
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++)
{
scanf("%d",&a[i]);
add(i,a[i]-a[i-1]);
}
for(int i=1;i<=m;i++)
{
int op;
scanf("%d",&op);
if(op==1)
{
int x,y,k;
scanf("%d%d%d",&x,&y,&k);
add(x,k);
add(y+1,0-k);
}
if(op==2)
{
int x;
scanf("%d",&x);
printf("%d\n",get(x));
}
}
return 0;
} 区间修改+区间查询
解决这个问题的方法较为复杂，但是我们很容易想到用差分的前缀和（还原原数组）的基础上再取前缀和
其中显然树状数组的询问方式可以帮助我们解决掉一次的求和，那我们怎么完成第二次的求和呢？
我们用a表示原数组，c表示差分数组可以发现a[1]+a[2]+...+a[x]a[1]+a[2]+...+a[x]=(c[1])+(c[1]+c[2])+...+(c[1]+c[2]+...+c[x])=(c[1])+(c[1]+c[2])+...+(c[1]+c[2]+...+c[x])=c[1]\times n+c[2]\times (x-1)+...+c[x]\times 1=c[1]×n+c[2]×(x−1)+...+c[x]×1即对于每一个c[i]c[i]在求和中的贡献应该为c[i]\times (x-i+1)c[i]×(x−i+1)故我们维护treea[i]treea[i]表示原差分数组，treeb[i]treeb[i]表示treea[i]\times (i-1)treea[i]×(i−1)
问题就能够迎刃而解！！！
1.这里是对于修改的实现
对于修改，我们修改treeatreea时只需要直接修改即可
至于修改treebtreeb我们也只需要变成
add(x,y):treeb[i]+=y\times(x-1)add(x,y):treeb[i]+=y×(x−1)可以证明其正确性，理由是乘法的分配率treeb[i]+=y\times(x-1)=k+a\times(x-1)+y\times(x-1)=k+(a+y)\times(x-1)treeb[i]+=y×(x−1)=k+a×(x−1)+y×(x−1)=k+(a+y)×(x−1)
其中aa、bb、kk均为常数
代码：
void add(int x,int y)
{
for(int i=x;i<=n;i+=lowbit(i))
{
treea[i]+=y;
treeb[i]+=y*(x-1);
}
return;
}2.这里是对于询问的实现
对于询问我们只需要按如下公式计算即可get(x):treea[i]\times x-treeb[i]get(x):treea[i]×x−treeb[i]
即=c[i]\times x-c[i]\times (i-1)=c[i]\times(x-i+1)=c[i]×x−c[i]×(i−1)=c[i]×(x−i+1)
也就是本章最开始推出来的那个公式
代码
int get(int x)
{
int sum=0;
for(int i=x;i>=1;i-=lowbit(i))
{
sum+=treea[i]*x-treeb[i];
}
return sum;
}模板：【模板】线段树 1
代码：
#include<bits/stdc++.h>
#define int long long
using namespace std;
int op;
int k;
int l,r;
int n,m;
int a[100001];
int treea[100001];
int treeb[100001];
int lowbit(int x)
{
return x&(-x);
}
void add(int x,int y)
{
for(int i=x;i<=n;i+=lowbit(i))
{
treea[i]+=y;
treeb[i]+=y*(x-1);
}
return;
}
int get(int x)
{
int sum=0;
for(int i=x;i>=1;i-=lowbit(i))
{
sum+=treea[i]*x-treeb[i];
}
return sum;
}
signed main()
{
std::ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
cin>>n>>m;
for(int i=1;i<=n;i++)
{
cin>>a[i];
add(i,a[i]);
add(i+1,-a[i]);
}
while(m--)
{
cin>>op;
if(op==1)
{
cin>>l>>r>>k;
add(l,k);
add(r+1,-k);
}
else
{
cin>>l>>r;
cout<<get(r)-get(l-1)<<endl;
}
}
return 0;
}
树状数组的应用
求逆序对
树状数组是求逆序对的利器，虽然归并排序也可以求逆序对，但是树状数组无论是从码量还是理解难度上都全面碾压归并排序
其实现逻辑非常简单，首先对于进行排序，然后用二分离散化（原因是逆序对要求严格单调）原数组在他们中的位置，按原数组的顺序加入即可求解即可。即统计大于它但在他之前出现的元素个数
同样三元的逆序对也可以这样求解，我们枚举中间的元素（不然无法知道另外两个元素的先后顺序与大小关系），正着求一次，倒着求一次，乘法原理求解即可
因为理解较为容易，因此这里直接附上例题和代码来帮助理解
模板1（二元逆序对）：P1908 逆序对
代码：
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int pre=5e5+10;
int n;
int a[pre];
int b[pre];
int place[pre];
int tree[pre];
int ans;
int lowbit(int x)
{
return x&(-x);
}
void add(int x,int y)
{
for(int i=x;i<=n;i+=lowbit(i))
{
tree[i]+=y;
}
return;
}
int get(int x)
{
int sum=0;
for(int i=x;i>=1;i-=lowbit(i))
{
sum+=tree[i];
}
return sum;
}
signed main()
{
std::ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
cin>>n;
for(int i=1;i<=n;i++)
{
cin>>a[i];
b[i]=a[i];
}
sort(b+1,b+1+n);
for(int i=1;i<=n;i++)
{
place[i]=lower_bound(b+1,b+1+n,a[i])-b;
}
for(int i=1;i<=n;i++)
{
add(place[i],1);
ans+=get(n)-get(place[i]);
}
cout<<ans;
return 0;
}模板2（三元逆序对）：Enemy is weak
代码：
#include<bits/stdc++.h>
using namespace std;
const int MAX=1e6+10;
int n;
int a[MAX];
int p[MAX];
int place[MAX];
int treebefore[MAX];
int treeafter[MAX];
int ansbefore[MAX];
int ansafter[MAX];
long long ans;
int lowbit(int x)
{
return x&(-x);
}
void addbefore(int x,int y)
{
for(int i=x;i<=n;i+=lowbit(i))
{
treebefore[i]+=y;
}
return;
}
int getbefore(int x)
{
int sum=0;
for(int i=x;i>=1;i-=lowbit(i))
{
sum+=treebefore[i];
}
return sum;
}
void addafter(int x,int y)
{
for(int i=x;i<=n;i+=lowbit(i))
{
treeafter[i]+=y;
}
return;
}
int getafter(int x)
{
int sum=0;
for(int i=x;i>=1;i-=lowbit(i))
{
sum+=treeafter[i];
}
return sum;
}
int main()
{
std::ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
cin>>n;
for(int i=1;i<=n;i++)
{
cin>>a[i];
p[i]=a[i];
}
sort(p+1,p+1+n);
for(int i=1;i<=n;i++)
{
place[i]=lower_bound(p+1,p+1+n,a[i])-p;
}
for(int i=1;i<=n;i++)
{
addbefore(place[i],1);
ansbefore[i]=getbefore(n)-getbefore(place[i]);
}
for(int i=n;i>=1;i--)
{
addafter(place[i],1);
ansafter[i]=getafter(place[i]-1);;
}
for(int i=1;i<=n;i++)
{
ans+=1ll*ansbefore[i]*ansafter[i];
}
cout<<ans;
return 0;
} 树状数组倍增
树状数组倍增的本质是倍增 （废话）
可以用于求出序列排名为kk的数在树状数组映射的原数组（意思是返回的是树状数组的下标，并非是原数组的值）中的位置
我们考虑到一个性质
tree[x|2^k]=a[x+1]+...+a[x|2^k]tree[x∣2k]=a[x+1]+...+a[x∣2k]
聪明的孩子可以想想这是为什么
所以我们可以证明思路可行性：
首先维护一个关于数列升序排序的各元素个数的树状数组，然后进行倍增
我们用和LCALCA一样的方式进行倍增，判一个边界，和一个<k<k
最后返回答案+1+1即可，不存在排名为kk的数当且仅当返回值为n+1n+1时
具体实现如下
int get(int o)
{
int s=0;
int now=0;
for(int i=log2(n);i>=0;i--)
{
int to=now|(1<<i);
if(to>n)
continue;
int x=s+tree[to];
if(x<o)
{
now=to;
s=x;
}
}
return now+1;
}模板：Multiset
代码：
#include<bits/stdc++.h>
using namespace std;
int n,q;
int k;
int tree[1000001];
int a[1000001];
int lowbit(int x)
{
return x&(-x);
}
void add(int x,int y)
{
for(int i=x;i<=n;i+=lowbit(i))
{
tree[i]+=y;
}
return;
}
int get(int o)
{
int s=0;
int now=0;
for(int i=log2(n);i>=0;i--)
{
int to=now|(1<<i);
if(to>n)
continue;
int x=s+tree[to];
if(x<o)
{
now=to;
s=x;
}
}
return now+1;
}
int main()
{
std::ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
cin>>n>>q;
for(int i=1;i<=n;i++)
{
cin>>a[i];
add(a[i],1);
}
while(q--)
{
cin>>k;
if(k<0)
{
int xx=get(abs(k));
if(xx!=n+1)
{
add(xx,-1);
}
}
else
{
add(k,1);
}
}
if(get(1)!=n+1)
cout<<get(1);
else
cout<<0;
return 0;
}
二维树状数组
二维树状数组的前置知识点是二维的前缀和和差分
我们分别来说一下
首先对于前缀和，我们维护一个该元素左上角的矩阵元素之和
对于任意矩阵之和的计算，我们根据容斥原理，得出
矩阵(a,b,c,d)=(1,1,c,d)-(1,1,a-1,d)-(1,1,c,b-1)+(1,1,a-1,b-1)(a,b,c,d)=(1,1,c,d)−(1,1,a−1,d)−(1,1,c,b−1)+(1,1,a−1,b−1)
然后考虑差分，差分作为前缀和的逆运算，其运算已经无需解释
我们重点来看差分的维护
我们很容易发现 （没错我注意力涣散了） 对于下图的矩阵(3,4,3,4)(3,4,3,4)加上一个xx，差分数组的变化如下
@ 1 2 3 4 5
1 0 0 0 0 0
2 0 0 0 0 0
3 0 0 +x 0 -x
4 0 0 0 0 0
5 0 0 -x 0 +x
这样我们就基本了解关于前缀和和差分的维护了
我们很容易想到利用这两个工具维护出二维树状数组的单点修改和区间查询（前缀和） 以及 区间修改和单点查询（差分）
这里附上两道模板题
但是对于区间修改和区间查询事情就有些复杂了
因为存在区间修改，所以我们还是考虑基于差分进行实现，不过我们需要对差分取两次前缀和，依旧考虑拆式子
发现在计算矩阵(1,1,x,y)(1,1,x,y)的时候，元素(i,j)(i,j)被计算了(x-i+1)(y-j+1)(x−i+1)(y−j+1)次
继续拆分
(x-i+1)(y-j+1)(x−i+1)(y−j+1)=(xy-xj+x)+(-yi+ij-i)+(y-j+1)=(xy−xj+x)+(−yi+ij−i)+(y−j+1)=(xy+x+y+1)-i(y+1)-j(x+1)+ij=(xy+x+y+1)−i(y+1)−j(x+1)+ij
所以我们考虑维护一个
原差分数组的11倍ii倍jj倍和ijij倍
然后就可以完成了
附上例题和代码
#include<bits/stdc++.h>
#define ll long long
#define ull unsigned long long
using namespace std;
int n,m;
int tree1[2050][2050];//*1
int tree2[2050][2050];//*i
int tree3[2050][2050];//*j
int tree4[2050][2050];//*ij
char op;
int a,b,c,d,k;
int lowbit(int x)
{
return x&(-x);
}
void add(int x,int y,int k)
{
for(int i=x;i<=n;i+=lowbit(i))
{
for(int j=y;j<=m;j+=lowbit(j))
{
tree1[i][j]+=k;
tree2[i][j]+=k*x;
tree3[i][j]+=k*y;
tree4[i][j]+=k*x*y;
}
}
return;
}
int get(int x,int y)
{
int sum=0;
for(int i=x;i>=1;i-=lowbit(i))
{
for(int j=y;j>=1;j-=lowbit(j))
{
sum+=tree1[i][j]*(x*y+x+y+1)-tree2[i][j]*(y+1)-tree3[i][j]*(x+1)+tree4[i][j];
}
}
return sum;
}
signed main()
{
std::ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
while(cin>>op)
{
if(op=='L')
{
cin>>a>>b>>c>>d>>k;
add(a,b,k);
add(a,d+1,-k);
add(c+1,b,-k);
add(c+1,d+1,k);
}
else if(op=='k')
{
cin>>a>>b>>c>>d;
cout<<get(c,d)-get(a-1,d)-get(c,b-1)+get(a-1,b-1)<<endl;
}
else
{
cin>>n>>m;
}
}
return 0;
}