解数独
编写一个程序,通过填充空格来解决数独问题。
一个数独的解法需遵循如下规则: 数字 1-9 在每一行只能出现一次。 数字 1-9 在每一列只能出现一次。 数字 1-9 在每一个以粗实线分隔的 3x3 宫内只能出现一次。 空白格用 '.' 表示。
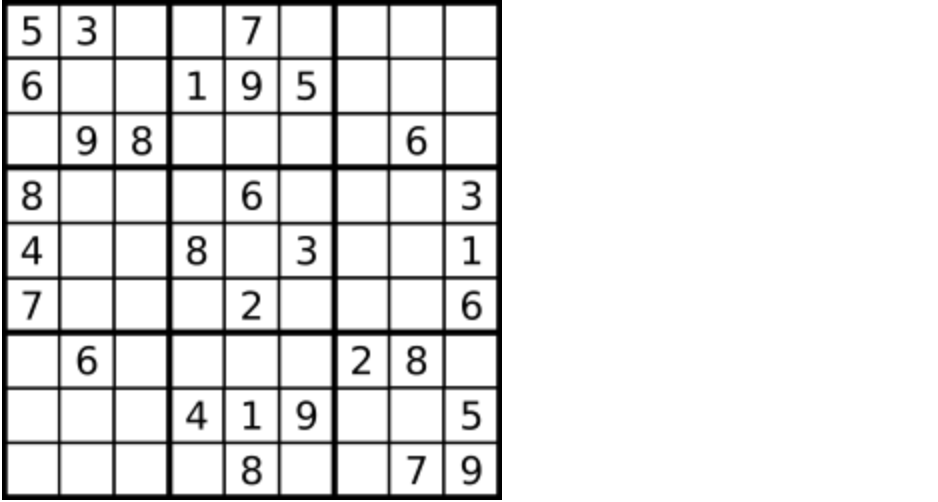
示例 1:
输入:board = [
["5","3",".",".","7",".",".",".","."],
["6",".",".","1","9","5",".",".","."],
[".","9","8",".",".",".",".","6","."],
["8",".",".",".","6",".",".",".","3"],
["4",".",".","8",".","3",".",".","1"],
["7",".",".",".","2",".",".",".","6"],
[".","6",".",".",".",".","2","8","."],
[".",".",".","4","1","9",".",".","5"],
[".",".",".",".","8",".",".","7","9"]]
输出:[["5","3","4","6","7","8","9","1","2"],
["6","7","2","1","9","5","3","4","8"],
["1","9","8","3","4","2","5","6","7"],
["8","5","9","7","6","1","4","2","3"],
["4","2","6","8","5","3","7","9","1"],
["7","1","3","9","2","4","8","5","6"],
["9","6","1","5","3","7","2","8","4"],
["2","8","7","4","1","9","6","3","5"],
["3","4","5","2","8","6","1","7","9"]]
解释:输入的数独如上图所示,唯一有效的解决方案如下所示:
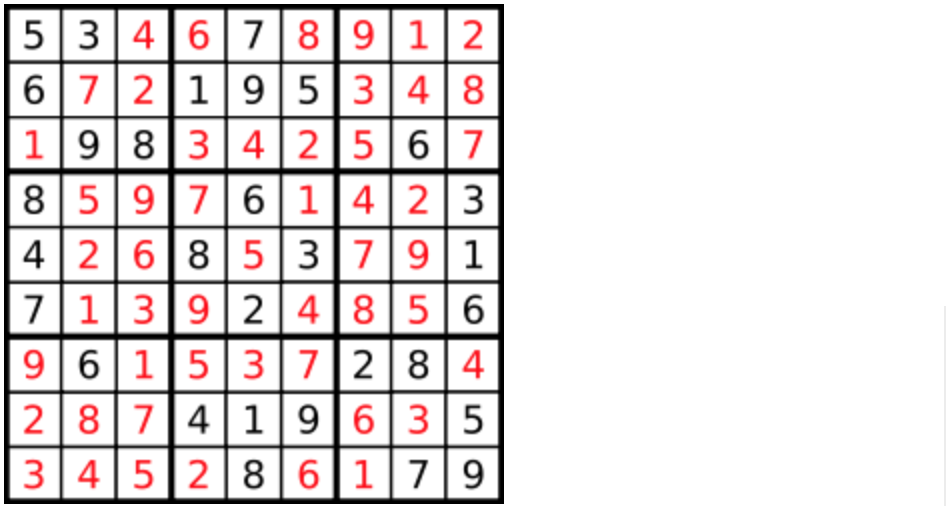
提示:
- 给定的数独序列只包含数字 1-9 和字符 '.' 。
- 你可以假设给定的数独只有唯一解。
- 给定数独永远是 9x9 形式的。
思路
看似跟N皇后差不多,好像也可以通过一层一层的递归进行遍历,然后填满所有空格
但是区别还是挺大的(反正用同样的思路是做不出来这题的)
从数独规则的角度来捋一捋解题思路
我们需要做的是去遍历"数独棋盘",该棋盘由9个3X3的小九宫格组成
往"数独棋盘"的每个空里面填数字,要求是同行列中不能出现与之相同的数
注意,我们每次填数字的对象都是"数独棋盘",也就是说,我们在一个递归层中需要处理的是一个二维数组,这就是本题与N皇后的区别
因此,在单层递归中需要引入两个for循环,一个负责遍历行,一个负责遍历列,这样才能定位"数独棋盘"中一个待填的格子,进而判断其中有没有数、需不需要填数、填的数合不合法
代码分析
基于上述分析,还是先来三部曲
三部曲
1、确定回溯函数的参数和返回值
题目的提示说了可以假定只有一个解,意思就是说我们不需要获取数独的所有可能解
那么,碰到(或者说填完)一个符合条件的解之后我们就应该立刻返回
是不是有点熟悉,没错,这种情况时,递归函数的返回值应该设置为布尔值,并且需要接受返回结果(详见路径总和)
而回溯函数的输入参数是"数独棋盘",不需要别的参数,因为本质上是去做一系列修改board的操作
class Solution {
private:
//确定回溯函数的参数和返回值
bool backtracking(vector<vector<char>>& board){
}
public:
void solveSudoku(vector<vector<char>>& board) {
}
};
2、确定终止条件
因为我们是要填满"数独棋盘"的每个格子,所以其实不需要终止,只要for循环结束就会自动终止,此时如果填完了就是找到一个结果,没填完就是当前数独无解
class Solution {
private:
//确定回溯函数的参数和返回值
bool backtracking(vector<vector<char>>& board){
//(确定终止条件,其实这里是不需要的)
}
public:
void solveSudoku(vector<vector<char>>& board) {
}
};
3、确定单层处理逻辑
这里就是本题的核心了,我们需要在这里遍历整个"数独棋盘",即遍历它的行和列
自然的,这需要使用两个for来完成
在for循环的最里层,先判断当前拿到的格子是不是空的,不是就跳过不用填,是就继续之后的逻辑
我们需要进行填数的逻辑,此时需要遍历数字1~9,判断当前通过两层for拿到的空格子应该填入哪个数字
这里是不是又很熟悉,没错,又™的需要一个判断函数isVaild来对填入的数进行规则判断(详见n皇后,不过这里两者没有联系)
这部分的总体步骤如下:
1、遍历行,即board里的元素
2、遍历列,即board里元素的元素(二维数组里的数组元素里的数值元素)
3、判断当前格子是否为空(空跳过,不空继续)
4、遍历1~9看哪个数合适填入
·每次遍历均使用规则判断函数进行判定
·返回true就填入当前数
5、触发递归,并接受递归函数的返回值,为true那本层也返回true
6、回溯,结束
class Solution {
private:
//确定回溯函数的参数和返回值
bool backtracking(vector<vector<char>>& board){
//(确定终止条件,其实这里是不需要的)
//确定单层处理逻辑
//两层for分别遍历行和列
for(int i = 0 ; i < board.size(); ++i){//遍历行,即board里的元素
for(int j = 0; j < board[0].size(); ++j){//遍历列,即board里元素的元素
if(board[i][j] != '.') continue;//当前格有值就跳过
//判断当前位置放1~9哪个数合适
for(char k = '1'; k <= '9'; ++k){
//判断当前格放k是否合适
if(isVaild(i, j, k, board)){//合适就放
board[i][j] = k;
if(backtracking(board)) return true;//注意了,这里是需要处理返回值的
board[i][j] = '.';
}
}
return false;//在当前空中判断1~9都不适合填入,那就是无解,直接返回false
}
}
return true;//遍历完所有格子没返回false,就说明填完了
}
public:
void solveSudoku(vector<vector<char>>& board) {
}
};
在写这部分代码时有以下注意事项:
1、要是捣不清现在是行还是列,就去题目给的实例看一下(注释里也有写)
2、递归时需要处理返回值
规则判断函数isVaild
判断棋盘是否合法有如下三个维度:
- 同行是否重复
- 同列是否重复
- 9宫格里是否重复
这里很容易把第三种情况漏掉,请特别注意一下
//规则判断函数,实现数独规则判定
bool isVaild(int row, int col, int curValue, vector<vector<char>>& board){
//在整个数独棋盘范围上
//判断行里是否有与curValue重复的值
for(int i = 0; i < 9; ++i){
if(board[row][i] == curValue) return false;
}
//判断列里是否有与curValue重复的值
for(int j = 0; j < 9; ++j){
if(board[j][col] == curValue) return false;
}
//在数独棋盘中的3X3的九宫格上
//设置每个小九宫格开始遍历的位置(每三个空格为一个小九宫格)
int miniblockRow = (row / 3) * 3;
int miniblockCol = (col / 3) * 3;
//判断小九宫格里有无重复值
for(int i = miniblockRow; i < miniblockRow + 3; ++i){//注意遍历条件,一次跳3格
for(int j = miniblockCol; j < miniblockCol + 3; ++j){
if(board[i][j] == curValue) return false;
}
}
return true;
}
再刷如果有问题再补充,TBD(23:00了我顶不住了)
完整代码
class Solution {
private:
//确定回溯函数的参数和返回值
bool backtracking(vector<vector<char>>& board){
//(确定终止条件,其实这里是不需要的)
//确定单层处理逻辑
//两层for分别遍历行和列
for(int i = 0 ; i < board.size(); ++i){//遍历行,即board里的元素
for(int j = 0; j < board[0].size(); ++j){//遍历列,即board里元素的元素
if(board[i][j] != '.') continue;//当前格有值就跳过
//判断当前位置放1~9哪个数合适
for(char k = '1'; k <= '9'; ++k){
//判断当前格放k是否合适
if(isVaild(i, j, k, board)){//合适就放
board[i][j] = k;
if(backtracking(board)) return true;
board[i][j] = '.';
}
}
return false;//在当前空中判断1~9都不适合填入,那就是无解,直接返回false
}
}
return true;//遍历完所有格子没返回false,就说明填完了
}
//规则判断函数,实现数独规则判定
bool isVaild(int row, int col, int curValue, vector<vector<char>>& board){
//在整个数独棋盘范围上
//判断行里是否有与curValue重复的值
for(int i = 0; i < 9; ++i){
if(board[row][i] == curValue) return false;
}
//判断列里是否有与curValue重复的值
for(int j = 0; j < 9; ++j){
if(board[j][col] == curValue) return false;
}
//在数独棋盘中的3X3的九宫格上
//设置每个小九宫格开始遍历的位置(每三个空格为一个小九宫格)
int miniblockRow = (row / 3) * 3;
int miniblockCol = (col / 3) * 3;
//判断小九宫格里有无重复值
for(int i = miniblockRow; i < miniblockRow + 3; ++i){
for(int j = miniblockCol; j < miniblockCol + 3; ++j){
if(board[i][j] == curValue) return false;
}
}
return true;
}
public:
void solveSudoku(vector<vector<char>>& board) {
backtracking(board);
}
};