1786. 从第一个节点出发到最后一个节点的受限路径数 (Medium)

问题描述

1786. 从第一个节点出发到最后一个节点的受限路径数 (Medium)

现有一个加权无向连通图。给你一个正整数 n ，表示图中有 n 个节点，并按从 1 到 n
给节点编号；另给你一个数组 edges ，其中每个 edges[i] = [uᵢ, vᵢ, weightᵢ]
表示存在一条位于节点 uᵢ 和 vᵢ 之间的边，这条边的权重为 weightᵢ 。

从节点 start 出发到节点 end 的路径是一个形如 [z₀, z₁,z₂, ..., zₖ]
的节点序列，满足 z₀ = start 、 zₖ = end 且在所有符合 0 <= i <= k-1
的节点 zᵢ 和 zᵢ+₁ 之间存在一条边。

路径的距离定义为这条路径上所有边的权重总和。用 distanceToLastNode(x) 表示节点 n 和
x 之间路径的最短距离。 受限路径 为满足 distanceToLastNode(zᵢ) > distanceToLastNode(zᵢ+₁) 的一条路径，其中 0 <= i <= k-1 。

返回从节点 1 出发到节点 n 的 受限路径数 。由于数字可能很大，请返回对 10⁹ + 7
取余 的结果。

示例 1：

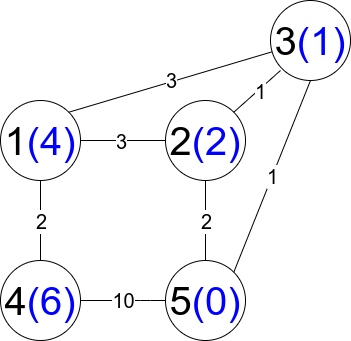
输入：n = 5, edges =
[[1,2,3],[1,3,3],[2,3,1],[1,4,2],[5,2,2],[3,5,1],[5,4,10]]
输出：3
解释：每个圆包含黑色的节点编号和蓝色的 distanceToLastNode 值。三条受限路径分别是：
1) 1 --> 2 --> 5
2) 1 --> 2 --> 3 --> 5
3) 1 --> 3 --> 5

示例 2：

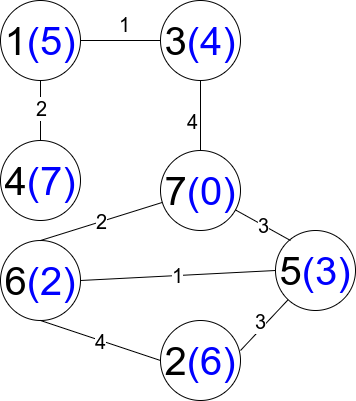
输入：n = 7, edges =
[[1,3,1],[4,1,2],[7,3,4],[2,5,3],[5,6,1],[6,7,2],[7,5,3],[2,6,4]]
输出：1
解释：每个圆包含黑色的节点编号和蓝色的 distanceToLastNode 值。唯一一条受限路径是：1 --> 3
--> 7 。

提示：

• 1 <= n <= 2 * 10⁴
• n - 1 <= edges.length <= 4 * 10⁴
• edges[i].length == 3
• 1 <= uᵢ, vᵢ <= n
• uᵢ != vᵢ
• 1 <= weightᵢ <= 10⁵
• 任意两个节点之间至多存在一条边
• 任意两个节点之间至少存在一条路径

解题思路

首先利用Dijkstra算法来计算各点到点n的最短距离，建立邻接表的时候，要注意本题的图是无向图，所以应该是：

vector<vector<vector<int>>> graph(n + 1);
for (auto &vec : edges) {
    graph[vec[0]].push_back({vec[1], vec[2]});
    graph[vec[1]].push_back({vec[0], vec[2]});
}

得到各点到n的最短距离之后，即可采用记忆化搜索来解决，从点i到点n的路径数即与i相连且满足条件的点到n的路径数之和。

代码

class Solution {
  public:
    int mod = 1000000007;
    void Dijkstra(vector<vector<vector<int>>> &graph, int n, vector<int> &dis, vector<int> &is_min) {
        auto cmp = [&](pair<int, int> &p1, pair<int, int> &p2) {
            return p1.second > p2.second;
        };
        priority_queue<pair<int, int>, vector<pair<int, int>>, decltype(cmp)> pq(cmp);
        pq.push({n, 0});
        while (!pq.empty()) {
            auto [idx, len] = pq.top(); // vec[0]表示坐标，vec[1]表示距离
            // cout << idx << " " << len << endl;
            pq.pop();
            if (is_min[idx] == 1) { // 说明已经找到最短路
                continue;
            }
            is_min[idx] = 1;
            dis[idx] = len;
            for (auto &tmp : graph[idx]) { // 遍历已经找到最短路的这个点的相邻边
                if (is_min[tmp[0]] == 0) {
                    pq.push({tmp[0], len + tmp[1]});
                }
            }
        }
    }
    int dfs(int idx, vector<vector<vector<int>>> &graph, int n, vector<int> &dis, vector<int> &is_min, vector<int> &cach) {
        if (idx == n) {
            return 1;
        }
        if (cach[idx] != -1) {
            return cach[idx];
        }
        int res = 0;
        for (auto &vec : graph[idx]) {
            if (is_min[idx] == 1 && dis[idx] > dis[vec[0]]) {
                res = (res + dfs(vec[0], graph, n, dis, is_min, cach)) % mod;
            }
        }
        cach[idx] = res;
        return cach[idx];
    }
    int countRestrictedPaths(int n, vector<vector<int>> &edges) {
        vector<vector<vector<int>>> graph(n + 1);
        for (auto &vec : edges) {
            graph[vec[0]].push_back({vec[1], vec[2]});
            graph[vec[1]].push_back({vec[0], vec[2]});
        }
        vector<int> dis(n + 1);
        vector<int> is_min(n + 1);
        vector<int> cach(n + 1, -1);
        Dijkstra(graph, n, dis, is_min); // 找到最短路径
        return dfs(1, graph, n, dis, is_min, cach);
    }
};