首页 > 其他分享 >多光源渲染方案 - Many Lights Sampling

多光源渲染方案 - Many Lights Sampling

时间：2023-03-10 12:23:50浏览次数：56  
标签：node 样本 light 蓄水池 复用 Sampling Lights 光源 Many

目录

light culling 的方式，可以极大剔除要处理的光源数量，但是可能有以下问题：

  • 实际光源的影响范围是无穷远的（通过 \(\frac{1}{\mathrm{dist}^2}\) 来实现衰减），强行设置有限影响范围（为了形成包围盒）会导致能量截断。
  • 面对 rect light，emissive triangle 等不可解析光源，光源影响范围包围盒不好确定

而 many lights sampling 的解决思路是只处理众多光源中的少量光源，但是让计算结果趋于无偏结果（无偏结果即相当于处理了所有光源）。

注意：many lights sampling 和 light sampling 是不同的，后者是在需要处理某一个不可解析光源的前提下，对其面积进行采样，从而算出该光源的贡献结果。在处理多个不可解析光源时，往往需要搭配 many lights sampling 方法：先通过 many lights sampling 选择处理哪几个光源，再对每个要处理的光源分别进行 light sampling。

Importance Sampling（IS）

当采用蒙特卡洛积分方法计算积分时，需要对被积函数 \(f\) 进行采样。

IS：可以按照分布 \(p\) 生成样本（其实就是采样），并且分布 \(p\) 越接近实际分布，那么收敛的速度就越快（所需的样本数 \(N\) 就可以更少了）：

\[I = \int f(x) dx \approx \frac{1}{N}\sum_{i=1}^{N}\frac{f(x_i)}{p(x_i)} \]

当 \(N\) 趋向无穷时，最右式便会等于 \(I\)。此外，要保持 IS 的无偏，需要保证被积函数 \(f(x)>0\) 的所有位置上，\(p\) 需 \(>0\)。

对于 many lights sampling 来说，虽然累积 lights 的贡献是离散的，但是太过多的光源数量可以让我们把它看成一种积分，并且需要设计一种采样分布 \(p\) 让重要的光源更容易被采样。

最简单的方式，例如：

我们可以用各个 light 的 intensity 来作为采样分布的依据（ intensity 大的光源更重要，即 pdf 应当更大）。

  • total intensity：计算出所有 lights 的 intensity 总和。
  • 某个 light 的 pdf：该 light 的 intensity 除于 totoal intensity
i = 0
sum = 0
r = rand in [0,1]
for i in range lightsNum
    sum += pdf_i
    if sum > r
        pick i to calculate L
        return L

当然，更进一步的优化是：提前建立好前缀和数组，这样就不必逐个累加 cdf，而是采用二分的方式计算 cdf。

Light BVH [2018~2019]

相关 paper：

Light BVH 类方法需要将所有光源转化成 emissive triangles，然后针对 emissive triangles 建立 BVH 结构来方便进行多光源的 IS 。

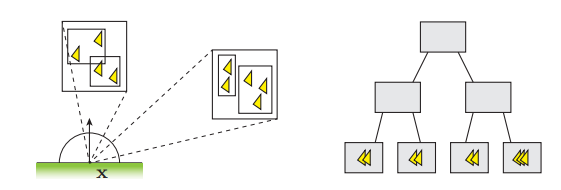
image-20230206201515957

Dynamic Many-Light Sampling for Real-Time Ray Tracing 提出采用两层 BVH 结构：bottom-level acceleration structure (BLAS) 和 top-level acceleration structure (TLAS)。

这其实就是类似于 ray tracing 里用于加速 ray-triangle 的 BVH 结构。

其中，一个 mesh instance 将对应一个 BLAS ，BLAS 的 leaf node 将存储若干个 emissive triangles；而 TLAS 的 leaf node 将存储一个 BLAS。

image-20230226213036035

图中每个黄色包围盒就是一个 BLAS 的 root node。

预构建 BVH

这部分其实可以用神经网络去针对场景训练一个最佳的 BVH 划分结构。

需要预先对所有 emissive triangles 划分，构建出一棵好的两层 BVH 树。

假设现在的 node 已经划分成了 L 和 R 两边，则可以有以下两种启发式去评判这种划分的好坏：

  • VH：考虑了两边子结点的 triangles 数量与形成的子包围盒体积。

\[\operatorname{cost}(L, R)=\frac{n(L) v(L)+n(R) v(R)}{n(L \cup R) v(L \cup R)} \]

\(n\) 代表了 node 的 triangles 数量，\(v\) 代表了 node 的包围盒体积。

  • VOH：在 VH 的基础上额外考虑了两边的光源朝向分布和光源功率。

\[\operatorname{cost}(L, R, s)=k_r(s) \frac{\Phi(L) v(L) M_{\Omega}(L)+\Phi(R) v(R) M_{\Omega}(R)}{a(L \cup R) M_{\Omega}(L \cup R)} \]

\(\Phi\) 代表了 node 里所有 triangles 组成的 cluster flux ，\(M_{\Omega}\) 代表了光源朝向的相似值。

更古早的方法有 SAH 和 SAHO，其实就是把包围盒体积项换成包围盒表面积项。

这样，我们就可以尝试所有的划分组合，然后根据评判启发式来选择最佳的划分组合来自底向上建立 BVH 树：

  • 建立 BLASes：以对应 mesh 的所有 triangles 为 leaf node，组建出一棵 BLAS；多个 mesh 便会对应输出多棵 BLASes。
  • 建立 TLAS：以 mesh 为 leaf node，组件出一棵 TLAS。

重建 BVH

预构建 BLAS 和 TLAS 之后，在运行时一旦某个 triangle 发生变化（如 triangle 发生 flux 变化，位置变化等），就需要更新它们。

  • refit BLAS：每帧在 GPU 里根据 emissive triangles 来更新 BLAS 结构的各个 node 属性，但不会改变 BLAS 树的结构。
  • refit TLAS：每帧在 GPU 里根据 mesh 来更新 TLAS 结构的各个 node 属性，但不会改变 TLAS 树的结构。
  • rebuild TLAS：每帧在 CPU 里根据 mesh 来重新划分 node，需要改变 TLAS 树的结构，并将新的 TLAS 结构 upload 给 GPU 的 refit TLAS 阶段。

image-20230226150410738

这样，一旦某个 emissive triangle 更新了，只会影响它所在的 BLAS 和 TLAS ，而不会影响其它的 BLASes，从而具有实时 rebuild BVH 的能力。

基于 BVH node 的 IS

不管是 TLAS 还是 BLAS，node 都应该额外存储以下属性：

  • \(C\): node 中心坐标
  • \(\Phi\): cluster flux，用于近似代表包含在内的所有 triangles 的 flux
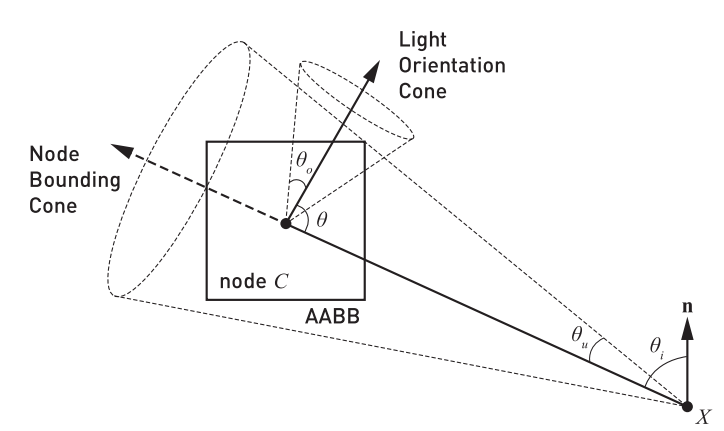
  • light orientation cone axis 和 \(\theta_o\) : 前者代表了 node 内所有光源朝向的中心朝向；后者代表了最远的光源朝向与 light orientation cone axis 的夹角。
  • \(\theta_e\) : 代表了围绕光源朝向的最远发射角

例如对于单个 emssive triangle 来说，\({\theta}_o = 0\) （因为只有一个法线朝向）， \({\theta_e = \frac{\pi}{2}}\) （因为在半球方向上会发射光）；而对于无数个 emissive triangles 组成的发光球来说， \({\theta}_o = \pi\) （因为该球的法线朝向布满了所有方向）， \({\theta_e = \frac{\pi}{2}}\) （因为每个 emissive triangle 都会在半球方向上会发射光）；对于 spot light 来说，\({\theta}_o = 0\)，而 \({\theta}_e\) 将取决于 spot light 的锥形半角。

image-20230227145156173

再举个例子：如图右两个 spot light 组成了一个 node，那么 light orientation cone axis 便是两个 spot light 光源朝向的中心向量，\(\theta_{o}\) 为最远的光源朝向到 light orientation cone axis 的夹角（node 仅有两个光源的情况下，两个夹角其实是一样的），\(\theta_{e}\) 则等于半角最大的那个 spot light 的半角。

这样有了 BVH 结构后，我们就可以用来做 many lights sampling 的 IS 了。每次对于 shading point \(X\)，我们可以自顶向下遍历 BVH 树。在遍历 node 时候往 node 中心投射一个可以刚好包住 node 包围盒的 cone，并通过以下公式判定一个 node 的 importance：

\[importance (X, C)=\frac{\Phi(C)\left|\cos \theta_i^{\prime}\right|}{\|X-C\|^2} \times \begin{cases}\cos \theta^{\prime} & \text { if } \theta^{\prime}<\theta_e, \\ 0 & \text { otherwise, }\end{cases} \]

其中，\(\theta_i'=max(0,\theta_i-\theta_u)\)，\(\theta'=max(0,\theta-{\theta}_o-{\theta}_u)\)

image-20230226145148891

这样就可以通过遍历 node 判断左结点和右结点的 importance，来让权重高的一边 node 更容易被选中。

image-20230227104920410

Real-time Stochastic Lightcuts [2020]

相关 paper：

  • Lightcuts: A Scalable Approach to Illumination [Walter 2005]
  • Real-Time Stochastic Lightcuts Proceedings of the ACM on computer graphics and interactive techniques. [Yuksel 2020]

莫顿序排序（Morton Order Softing）

在 view space 下，每个 light 的位置编码成 Morton code（30 bits，x/y/z 分别占 10 bits），并利用 双调排序（Bitonic Softing） 来排序。

简单介绍下莫顿序：莫顿序有一个这样好的性质——序列里邻近的元素在空间上也会比较邻近。并且，莫顿序排序的结果就隐含了空间的层次，从而不需要构建真正的 BVH 结构。

2D 莫顿序：

undefined

3D 莫顿序：（序列邻近则体现出颜色相近）

img

再简单介绍下双调排序：通常基于比较的 CPU 排序复杂度在 \(O(n\log n)\) ；而双调排序是针对并行计算而生的算法，复杂度为 \(O(n(\log n)^2)\)，然而得益于 GPU 的巨量线程数，算法复杂度中的 \(n\) 是可以独立并行的，也就是说实际复杂度为 \(O((\log n)^2)\)。关于该排序算法的细节，可参考 DirectX11 With Windows SDK--27 计算着色器：双调排序 - X_Jun - 博客园。

构建 Light Tree

为了满足 GPU 的并行化计算，论文采用完美二叉树作为 light tree 的结构，省去了指针的表示（因为索引本身就暗含了结点关系）。这样，就可以按以下流程构建 light tree：

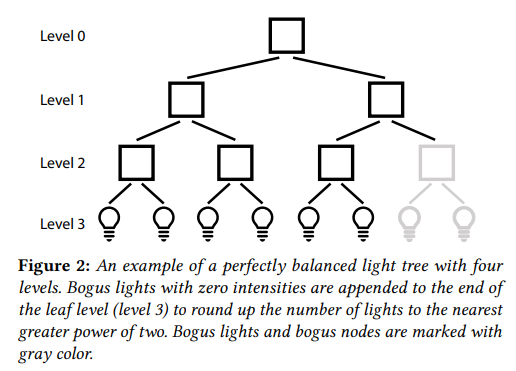
  • 一个叶结点存储一个 light id，将已经进行莫顿序排序的 light 按序一个个填入完美二叉树的最低层级，若不能填满，则加入 false lights（flux 为 0 的假灯）直至填满。
  • 从最低层开始自底向上构建父结点（同一层的计算可并行化）：只需要将两个子结点的 intensity 直接相加作为父结点的 intensity，和计算出能包围两个子结点的 AABB 大小。

image-20230227173324163

基于 Lightcuts 的 IS

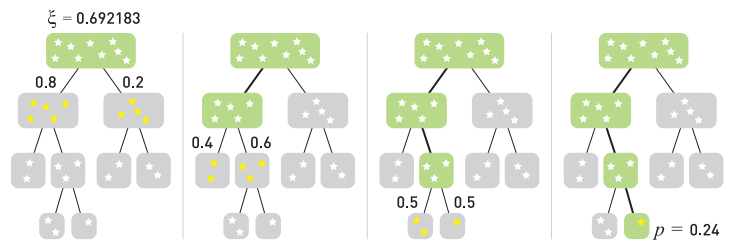
有了 light tree 后，我们就可以自顶向下遍历，并根据概率选择一个子结点往下走，直到选择的结点 light 数量小于等于 lightcuts 所限制的 light 数量。

stochastic lightcuts 的早期论文是需要预构建 light tree，并且父结点不是简单的子结点 intensity 相加，而是用复杂的算法计算出一个可以代表两子结点的表征光源（包含位置和强度等）。然后在 sampling 时也一样自顶向下往下走，但对于路径中没有走的 brother node，将直接使用它的表征光源来代表，这种方式其实是有偏的，不过收敛是很快。

而这种自顶向下的走法就像是刀往 light tree 上 cut 来 cut 去，所以称为 light cut。

不过现在这个 real-time stochastic lightcuts 只是一个纯粹的 importance sampling 方法，具有无偏的性质。

每个子结点（假设为 node \(j\) ）的 importance 计算如下：

\[w_j^{\min }=\frac{F_j(\mathrm{x}, \omega)\left\|\mathbf{I}_j\right\|}{\left(d_j^{\min }(\mathrm{x})\right)^2} \quad w_j^{\max }=\frac{F_j(\mathrm{x}, \omega)\left\|\mathbf{I}_j\right\|}{\left(d_j^{\max }(\mathrm{x})\right)^2} \]

\(F_j(x,\omega)\) 为反射率界限（一般就是剔除无关参数的 brdf 项），\(\mathbf{I}_j\) 为 node 的 intensity，\(d^{min}\) 和 \(d^{max}\) 分别代表 shading point x 到该 node 的 AABB 的最近距离和最远距离。

特殊地，当 shading point 在 node 的包围盒内，其 \(d^{min}\) 和 \(d^{max}\) 均为 0，这时候同时忽略两个 node importance 的 \(d\) 相关项。

然后选择 node \(j\) 的概率即为 \(p_j^{min}\) 和 \(p_j^{max}\) 的一半：

\[p_j^{\min }=\frac{w_j^{\min }}{w_j^{\min }+w_k^{\min }} \quad p_j^{\max }=\frac{w_j^{\max }}{w_j^{\max }+w_k^{\max }} \]

\[p_j=\left(p_j^{\min }+p_j^{\max }\right) / 2 \]

使用 min 和 max 的一半是为了同时考虑最坏情况和最好情况（如包围盒可能过大，x 与 AABB 的距离可以接近于0，最远的却可以拉到无穷远），虽然个人觉得还是很 hack。

Cut Sharing

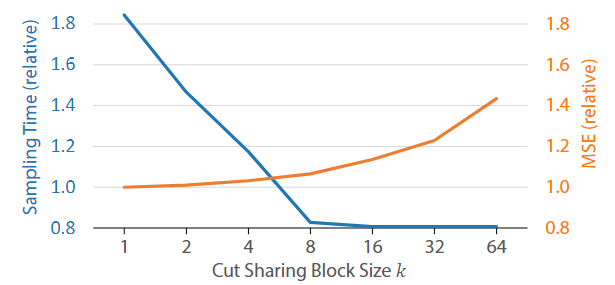
相邻的 pixel 因为距离较近，因此它们通常具有相同的 cut 法，这就造成了一些 sampling 的浪费。

我们可以用一组相邻的 pixels 去做一次包含较多 light 数量的 cut，而不是对每个 pixel 分别去做一次包含较少 light 数量的 cut。这种空间复用的思路可以极大减少 sampling 时间，但是当然也会随着组内 pixels 数量的增多而更加有偏：

image-20230227235318572

ReSTIR（Reservoir Spatio-Temporal Importance Resampling）[2020]

相关 paper：

  • Spatiotemporal reservoir resampling for real-time ray tracing with dynamic direct lighting [BENEDIKT 2020]

ReSTIR 是近期实时渲染的热门前沿方向，许多渲染算法都可以用到这种采样思想。ReSTIR 应用在直接光照的时候，可以很好的应对 many lights sampling 的问题。

Resampled Importance Sampling (RIS)

假设我们有一个极度贴近实际分布的好分布 \(\hat{p}\)，但它不好生成样本，只适合评估样本；另一方面，我们又有另一个比较简单的分布 \(p\) ，虽然它简单地足以能够生成样本，但是这个分布又比较偏离实际分布。

RIS：先用简单分布 \(p\) 生成 \(M\) 个样本，再从这 \(M\) 个样本用复杂分布 \(\hat{p}\) 再挑出 1 个样本（要用 RIS 输出 \(N\) 个样本，也只需要独立地调用 N 次 one-sample RIS 即可）。RIS 的效果一般来说要好过纯粹用 \(p\) 来进行 IS。

不过要保持 RIS 的无偏，需要保证被积函数 \(f(x)>0\) 的所有位置上，\(p\) 和 \(\hat{p}\) 都需 \(>0\)。

\[I = \int f(x) dx \approx \frac{f(y)}{\hat{p}(y)} (\frac{1}{M}\sum_{j=1}^{M}\mathrm{w}(x_{j})) \]

\(x_{j}\) 为 \(p\) 生成的第 \(j\) 个样本，\(y\) 为 \(\hat{p}\) 挑选出的样本。

\[\mathrm{w(x)} = \frac{\hat{p}(x)}{p(x)} \]

当然实际上挑样本是根据权重 \(\mathrm{w}\) 来挑：因为生成的 \(M\) 个样本中每个样本生成的概率是不同的，所以需要除掉 \(p\) 抵消掉这个概率，接着便是通过乘 \(\hat{p}\) 来决定哪个样本更容易被挑中。

原论文伪代码如下：

image-20230301145442050

Weighted Reservoir Sampling (WRS)

原本最原始的 RIS 算法便是先用简单分布 \(p\) 生成 M 个样本再用复杂分布 \(\hat{p}\) 去挑一个样本，但是这需要占用 M 个样本存储空间；而 WRS 聪明地将 RIS 的算法改造成了流式算法，让空间复杂度与 M 无关（只需要记录三个属性），这就意味着甚至 M 无穷大都可以容纳（精度足够的情况下）。

核心就是改造成了一个蓄水池结构（reservoir），它只需要存储：

  • \(y\)：一个用于输出的样本，也可以理解成经过 \(M\) 次输入后留下来的 winner 样本。
  • \(\mathrm{w}_{sum}\)：输入过的样本的权重 \(\mathrm{w}\) 总和。
  • \(M\)：输入过的样本数量。

然后可以源源不断给蓄水池输入新样本，每次输入新样本时它便会根据权重 \(\mathrm{w}\) 去决定留下旧样本还是留下新样本。

这种逐次淘汰样本的方式，和原始 RIS 先生成一堆样本再选一个 winner 样本的方式，在本质上是一致的，可以自行推理一下数学逻辑。

原论文伪代码如下：

image-20230304223607904

基于屏幕空间的多光源 RIS

接下来将用 WRS 应用到直接光照着色的 many lights sampling 上，然后用于 RIS 的简单分布和复杂分布分别如下：

  • source pdf \(p\) ：归一化的 intensity pdf，光源强度越大的光源则越容易被挑中。
  • target pdf \(\hat{p}\) ：lighting pdf，即着色函数除了 visibility 的部分，更加贴合着色函数的分布（实际分布）。

预处理光源

预先将所有光源的 intensity 总和 \(I_{total}\) 计算出来和建立好 \(I\) 的前缀和数组，这样在后续通过 \(p\) 生成候选样本时就不必逐个累加 cdf，而是采用二分的方式计算 cdf。

\(p(x_i) = \frac{I(x_i)}{I_{total}}\)

pixel 蓄水池

每个 pixel \(q\) 包含一个蓄水池，然后在一帧内可以给它输入 M 次 \(p\) 生成的候选光源样本，此时蓄水池的 \(y\) 便是最终挑选的光源样本，便可以用来计算它对 pixel 的贡献：

\[I = \int f(x) dx \approx \frac{f(y)}{\hat{p}(y)} (\frac{1}{M}\sum_{j=1}^{M}\mathrm{w}(x_{j})) \]

顺便需要记录一下蓄水池的当前样本权重 \(\mathrm{w}\)，可见公式推导。

原论文伪代码如下：

image-20230305173402395

效果图：

图中下面的方式是 Light BVH 方法，而上面的方式则是不同 \(M,N\) 的 RIS 方法。

image-20230305173303968

有偏时空复用

上面我们知道， \(M\) 的数量足够多时，RIS 的效果会变得相当好，但是 pixel \(p\) 每帧生成足够多的候选样本也同样很费时，一个很自然的想法是能不能在时序上和在空间上复用样本来增加样本数：

空间复用（spatial reuse）：当前 pixel \(p\) 和附近的 pixels 往往在几何和材质上是非常相似的，可以进行空间上的复用。

  • 可以对周围 \(k\) 个 pixels 的蓄水池进行一次组合：这样每个 pixel 只需要耗费 \(O(k+M)\) 的时间而获得 \(O(k\cdot M)\) 个候选样本。
  • 甚至这种组合是可以多次迭代的（假设迭代了 \(n\) 次），从而让 pixels 的蓄水池样本扩散到更多别的 pixels：耗费 \(O(nk+M)\) 的时间而获得 \(O(k^n M)\) 个候选样本。

时间复用（temporal reuse）：将当前 pixel \(p\) 投影到上一帧，并找到投影位置附近的 previous pixels，它们往往在几何和材质上也是非常相似的，可以进行时序上的复用。

  • 直接组合上一帧投影位置附近的 previous pixels 的蓄水池，随着帧数的累积（假设累积了 \(t\) 帧）便可以有 \(O(t\cdot(k^nM))\) 个候选样本。

可见性复用（visibility reuse）：候选样本数接近无限多时，样本分布也基本接近 target pdf \(\hat{p}\) ，但还是无法实现无噪渲染。毕竟真正的分布是 \(\hat{p}\cdot V\)，也就是说引起噪声的因素就剩下了 visibility \(V\)。

  • 为了减少 visibility 噪声的传播，每个蓄水池在执行时空重用前，需要对自己的输出样本进行一次 shadow ray 检测自己的输出样本 \(y\) 是否有效，若无效，则将 \(W\) 置为 0，避免传播到相邻的蓄水池。
image-20230305224436632

具体组合蓄水池的伪代码如下：

image-20230305121454045

可以这么理解：假设我们要合并蓄水池 \(r\) 到 \(s\)，实际上做的就是把 \(r\) 所有候选样本再次逐个输入到 \(q\)，因此需要重新累积 \(q\) 的 \(\mathrm{w}_{sum}\) 和 \(M\)。

而用 \(r.W\) 乘上 \(r.M\) 就能得到 \(\frac{r.\mathrm{w}_{sum}}{\hat{p_{r}}(y)}\)，即实际更新权重为 \(\hat{p}_q(r . y) \cdot r . W \cdot r . M = \frac{\hat{p_q}(r.y)}{\hat{p_r}(r.y)}\cdot r.\mathrm{w}_{sum}\) 。但毕竟输入给 \(q\) 的只有这 \(M\) 个样本中的一个而不是输入了 M 个样本，因此除 \(\hat{p_r}(r.y)\) 是为了抵消掉选这个 y 样本的概率，再用 \(\hat{p_q}(r.y)\) 评估这 M 个样本的质量。

无偏时空复用

实际上，上面的时空复用忽略了一个细节：pixel \(q\) 附近的 pixels 或者投影到上一帧的附近 pixels 在几何和材质上虽然接近，但不完全一样，也就是说这些 pixels 各自的样本空间是不同的，这就会导致偏差的诞生。

具体如何分析偏差建议可以看原论文，此处只写博主的大概理解。

前面 RIS 的理论我们知道：在某个样本空间中，被积函数 \(f(x)>0\) 的所有位置上，\(p(x)\) 和 \(\hat{p}(x)\) 都需 \(>0\)。

  • 因为 \(p\) 是 intensity pdf，它在任何样本空间总是能满足 \(p>0\) 。
  • 而假设我们通过了时空复用后得到了一个样本 \(y\) ，既然能选中该样本，那就说明可能会得到 \(f(y)>0\) （取决于 visibility）；假设某些时候，visibility 为 1，也就是说在被复用的各个 pixel 样本空间中 \(f(y)\) 均被视为 \(>0\) 了，但是在其中某些样本空间中 \(\hat{p}(y)\) 却实际是为 0 的，这就违反了 RIS 的无偏规则。

因此，我们通过时空复用后，得到本次的样本输出 \(y\)，再对被复用的 pixels 蓄水池做一遍检查，看看在它们各自的样本空间中 \(\hat{p}(y)\) 是否 \(>0\) ；若没通过检查，则该蓄水池的样本数不算入本次输出的 \(W\)。

image-20230305230807184

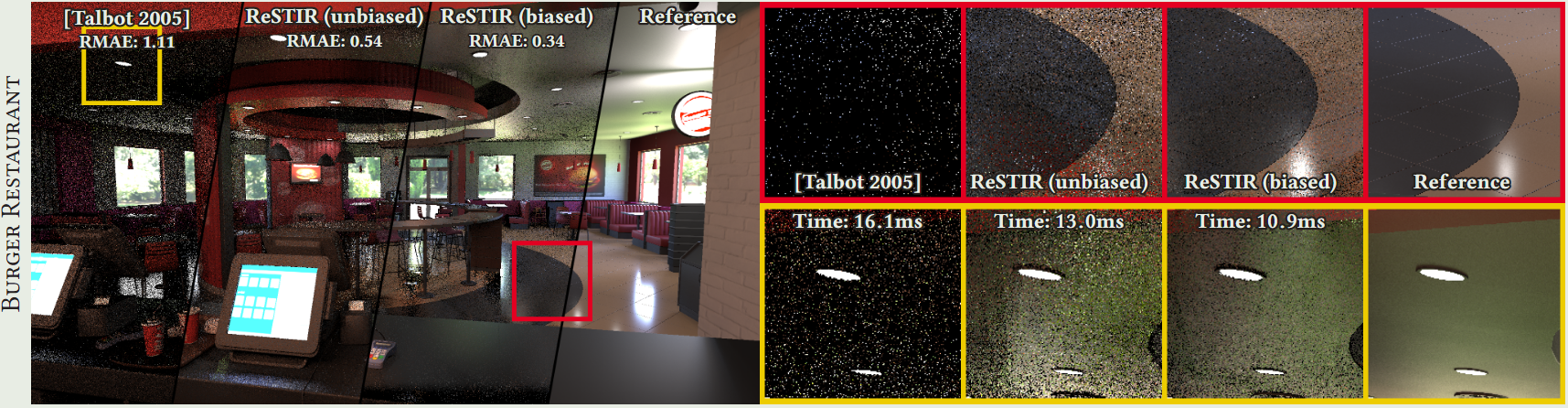
引入无偏的时空复用后，候选样本的数量可能就不会像有偏方法那么多，因此收敛更慢；而且还引入了一些额外的计算（主要指重新检查一边蓄水池），导致更加耗性能。下面是一些效果比较：

image-20230306141643350

image-20230306141709868

ReGIR [2021]

相关资料：

  • Rendering Many Lights with Grid-based Reservoirs [2021]

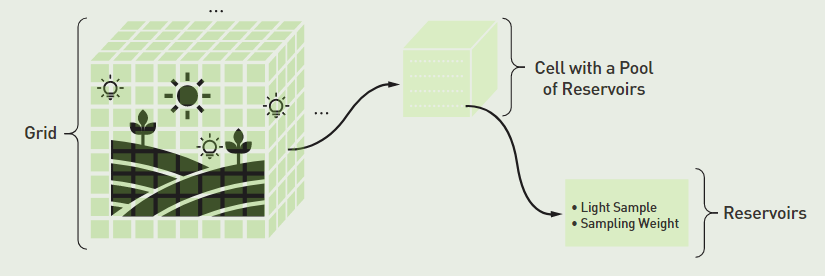
核心就是将 RIS 同时应用到 grid 和屏幕，即：用 cell 蓄水池先粗略采集一波光源样本，再让 pixel 抖动一下找到对应的 cell 并将该 cell 的蓄水池样本再输入到 pixel 蓄水池，最终选定哪个光源样本用于 pixel 的 shading。

其实思想就是空间复用，毕竟部分 pixels 是在同一个 cell 里，先在 cell 里用粗略的 target pdf 才一遍后，就可以留下了质量还可以的样本；而 pixels 就可以用精确的 target pdf 从这些样本中挑选，而不是从 IS 里生成的样本（基于 intensity 的 IS 所生成的样本质量还是挺差的）里挑选。

ReGIR 效果图：

可以看到 ReGIR 在 many lights sampling 的效果中比基础 RIS 收敛还要快。

image-20230308153454148

基于 Grid 的多光源 RIS

light slot 蓄水池

每个 cell 存储若干个蓄水池（原文里称为 light slots，一个 light slot 其实就是对应一个蓄水池），原文默认是每个 cell 包含 512 个蓄水池，实际上也就隐含了有 512 个输出用的光源样本（即 \(N=512\)）。

image-20230308153225241

每个蓄水池都可以独立地进行 stream RIS 流程，其两个 pdf 分别为：

  • source pdf \(p\) ：每个光源都相同的概率，即为 \(\frac{1}{\mathrm{NumLight}}\)
  • target pdf \(\hat{p}\) ：\(\frac{\mathrm{I}}{r^2}\)

其中 \(\mathrm{I}\) 为光源的 intensity，\(r\) 为光源到本 cell 中心的位置。

float3 lightVector = candidate.position - gridCellCenter;
float lightDistanceSquared = max(gMinDistanceSquared , dot(lightVector , lightVector));
float sourcePdf = <Source PDF as described , e.g., uniform sampling >;
float targetPdf = sample.intensity / lightDistanceSquared;

可以看到这个 source pdf 非常简单，实现上就是随机选一个光源；而 target pdf 则是考虑了 intensity 和距离衰减因素。

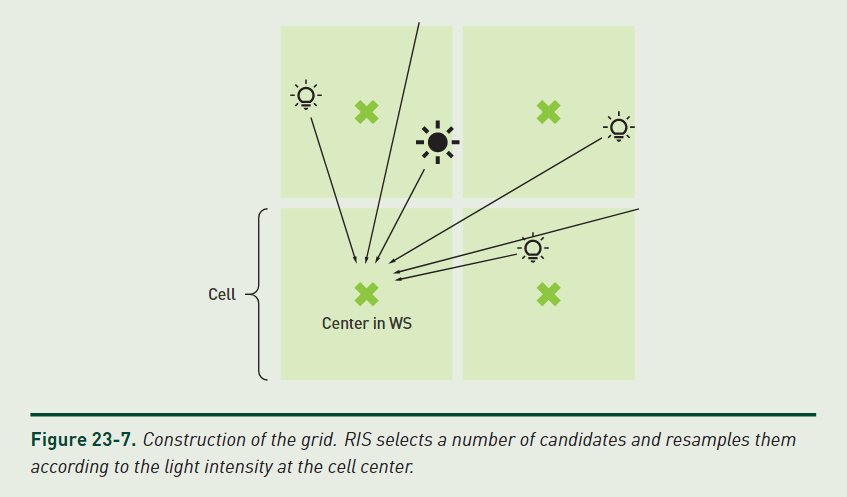
image-20230308153318915

原文在蓄水池中默认采 \(M=8\) 个候选样本，再增加候选样本数带来的收益会有边际效应。

个人认为，cell 没有使用一个大型蓄水池（\(M=512*8\) 个候选样本）而是分成 512 个小型蓄水池（\(M=8\)）来其实是为了让算法高度并行化，代价就是额外的空间开销。

时序复用

light slot 蓄水池没有空间复用。

时序复用：对前面若干帧的历史蓄水池分别拿来复用，默认为 8 帧，也就是说需要存储 8 份历史蓄水池。

此外，为了避免每个 light slot 蓄水池的 \(M\) 增长到无穷大，再输入完样本后（包括复用的样本），需要将 \(M\) 重置为 1，当然对应的 \(\mathrm{w}_{sum}\) 也应该除掉 \(M\) 。

// Merge new reservoir with reservoirs from previous frames.
for (int i = 0; i < GRIDS_HISTORY_LENGTH ; i++) {
	lightSlotReservoir = mergeReservoirs(lightSlotReservoir, gLightGridHistory[i][lightSlotIndex]);
	
	// Divide wSum by M after each combining "round ."
	lightSlotReservoir.totalWeight /= lightSlotReservoir .M;
	lightSlotReservoir.M = 1;
}

这里我比较困惑为什么不直接复用上一帧，逐帧累积，而是复用了 8 帧的信息。可能是因为蓄水池每次重置 \(M=1\) 导致历史帧样本只有一个而不能累积，复用效果较差，因此不得不存储 8 帧的历史蓄水池。但个人觉得这块是有很大改进空间的。

有了上述介绍，我们先看看原本蓄水池的组成：

  • 输出样本 \(y\)
  • 总权重 \(\mathrm{w}_{sum}\)
  • 总样本数 \(M\)
  • 输出样本的权重 \(W=\frac{1}{\hat{p}(y)}(\frac{\mathrm{w}_{sum}}{M})\) ，实际上该权重的倒数便是输出样本 \(y\) 的概率。

而现在 light slot 蓄水池可以简化成如下形式来存储：

  • 输出样本 \(y\)
  • 平均权重 \(\mathrm{w_avg}\)
  • （无需存储，隐含信息）\(M=1\)
  • （无需存储，可低成本地立即计算 \(\hat{p(y)}\) 出来）输出样本的权重 \(W=\frac{1}{\hat{p}(y)}(\mathrm{w_avg})\) ，实际上该权重的倒数便是输出样本 \(y\) 的概率。

动态光源问题

动态光源权重发生明显变化时，然后假如历史蓄水池的输出样本刚好是那个动态光源，那么它的权重也不会发生变化（因为没有去修改历史蓄水池权重的操作），就会导致 noise。

为此解决方式有两种：

  • 防止输出样本为动态光源的蓄水池参与时间重用（更推荐这个做法）。
  • 为历史蓄水池重新评估动态光源的权重（更费时）。

基于屏幕空间的多光源 RIS

pixel 蓄水池

这个与 ReSTIR DI 类似，每个 pixel 蓄水池都可以独立地进行 stream RIS 流程，其两个 pdf 分别为：

  • source pdf \(p\) ：light slot 蓄水池输出样本的权重的倒数 \(\frac{1}{r.\mathrm{w}}\) 。
  • target pdf \(\hat{p}\) ：可以选择完整的 BRDF，实际上就是渲染方程刨去了 visibility 的部分。

如果评估完整 BRDF 比较费时，可以只使用部分的 BRDF 成分来评估，从而简化计算。

float sourcePdf = candidate.sampleTargetPdf / reservoirAverageWeight;
float targetPdf = PartialBrdf(candidate , shadedPoint);

light slot 蓄水池接入 pixel 蓄水池

如何把 light slot 蓄水池接入 pixel 蓄水池呢？很简单，pixel 直接根据世界空间坐标位置并做一定的 jittering 然后定位到对应的 cell，遍历该 cell 的 light slots 即可（512 个 light slot 蓄水池意味着需要输入 512 个候选样本）。

jittering 是为了避免 pixel 刚好在 cell 边界而产生的 artifact，因此才给它一个 cell 范围的 jittering：

// Jitter hit point position within the size of grid cell.
float3 gridLoadPosition = pointPosition +( float3(rand (), rand (), rand ()) * 2.0f - 1.0f) * gHalfGridCellSize;
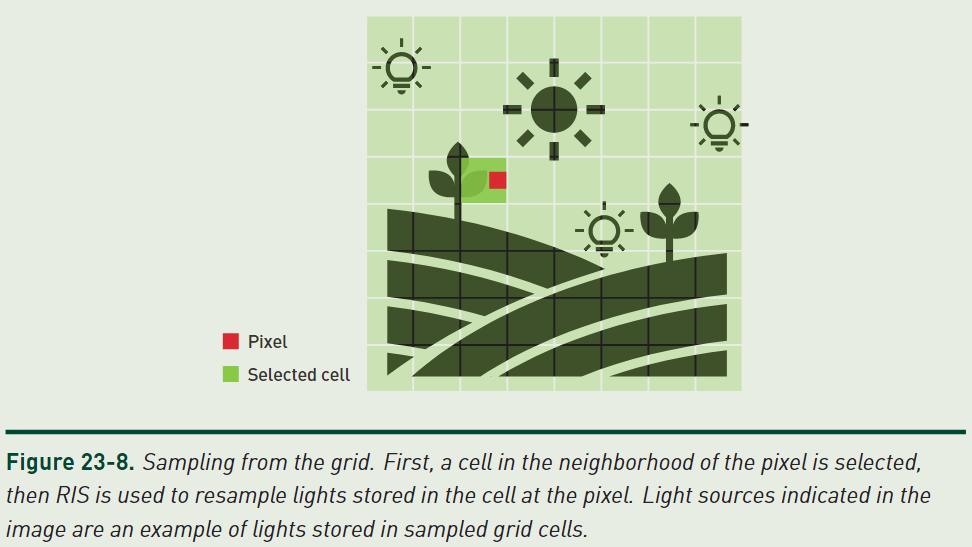
image-20230308154322425

时空复用

和 ReSTIR 差不多，复用空间上的 pixel 蓄水池和时序上的 pixel 蓄水池，不多阐述。

优化

grid 结构

传统的 grid 结构可能会占据过多存储空间或性能开销，可以选择以下方式改进：

  • Scrolling Clipmap：利用滚动优化可以避免更新所有 cells 的蓄水池，性能较好，但对于远处的坐标可能就没有 cell 从而无法做多光源。
  • Sparse Grid：大世界坐标友好，但需要解决哈希冲突，性能略低。

跳过无关 cell 的填充

对于没有几何体的空间部分，我们可以跳过对应 cell 的填充，减少大量 cells 的更新。实现这个 idea，我们需要对每个 cell 存储一个 counter（只需要几位的整数），然后每一帧：

  • 要是 cell 被访问了，可以将 cell 的 counter 重置为最大值。
  • 要是 cell 没有被访问，就给该 cell 的 counter 减一，最多减到 0。

这样我们就可以对那些 counter 为 0 的 cells 跳过更新 light slots 的步骤。

image-20230308153906533

可伸缩更新

从上文的思路出发可以更进一步调整更新 cell 的 light slots 频率（可以改变对 light slots 输入的样本数量或者 light slots 蓄水池的数量），例如：

  • counter 越少，更新频率越低。
  • 距离越远，更新频率越低（LOD）。
  • ...

扩展到其它渲染方案

只要把次级光源也当成光源，该方法也可以很容易推广到其它 GI 方法，例如 VPL 类方法等。

参考

标签：node,样本,light,蓄水池,复用,Sampling,Lights,光源,Many
From： https://www.cnblogs.com/KillerAery/p/17202961.html

相关文章

赞助商

阅读排行

网站主页关于我们联系我们网站地图

本网站内容转载自其他媒体，侵权联系[admin##ips99.com]。

Copyright © 2020-2023 IPS99 版权所有 IPS99