Title
“Plan Stitch: Harnessing the Best of Many Plans” (Ding 等, 2018, p. 1123) 【
计划缝合:利用众多计划的精华/最优
两个关键点:
- 缝合
- 精华/最优
对本科毕设的最后一步或许有帮助:基于Plan模版进行拼接和修改。
】
Abstract
“ABSTRACT” (Ding 等, 2018, p. 1123) 【
摘要:
背景:
查询优化器选择一个非最优的查询执行计划,会导致查询性能的下降。
现如今的商业 DBMS 会选择使用 Reversion-based plan correction 来解决该问题。其原理是在检测到出现查询性能降低时,重新纠正——使用之前仍然有效且具有最低执行代价的旧计划。
真正的发现:
RBPC 的基本原理使得其风险很小,但是忽略了更加有效的优化方式——从之前执行计划的高效 *子计划* 中获得潜在价值的信息!这会比单独旧的执行计划 代价更低。
研究成果:
在 Microsoft SQL Server 之上实现 Plan Stitch 方法,经过 TPC-DS 测试,显著降低执行代价。
】
Introduction
“INTRODUCTION” (Ding 等, 2018, p. 1123) 【
引言:
关于什么:
同一个查询所得到的查询计划会因为各种原因更改,更改之后可能会导致 计划回归 的问题,具体表现就是优化器所选择的最新查询计划执行代价比原先高。
但是目前商业数据库系统中的解决方法—— RBPC 所生成的计划效率上上升空间还很大。
解决的方法:
在 Microsoft SQL Server 的基础上,实现了 Plan Stitch ,是一个比 RBPC 更高效的 APC 策略。
通过考虑同一个查询的 过去已执行的计划以及其子计划:
- 在受限制的搜索空间(有相同的逻辑表达式,并且在当前的配置环境中有效)中,通过比较相同逻辑表达式的可替代子计划,来发现高效的子计划;
- 用 基于动态规划算法 的高效、二次时间复杂度的算法将这些高效子计划,合并成在执行代价上最低的缝合计划;
- 用计划强制特征来影响优化器的计划选择,以验证计划的有效性。
迷人的地方:
在 RBPC 的基础上,找到了可以提升的地方:在物理算子层面对执行代价进行优化,通过已执行计划的子计划缝合来体现。
拥有三个特点:
- 全自动
- 低开销
- 低风险
新颖的地方:
将过去已执行的计划的子计划进行缝合。
眼前一亮的结论:
通过 TPC-DS 和三个真实的用户负载当做实验环境,发现 Plan Stitch 相比较于 RBPC 的提升很大。
】
Overview
“OVERVIEW” (Ding 等, 2018, p. 1125) 「
Overview:
问题陈述:
Plan Stitch 为给定的查询 q 构建一个有最低执行代价的查询计划 p,p有一个限制:在p中的每一个算子,都只能从 过去已执行的计划 中获取。
架构概述:
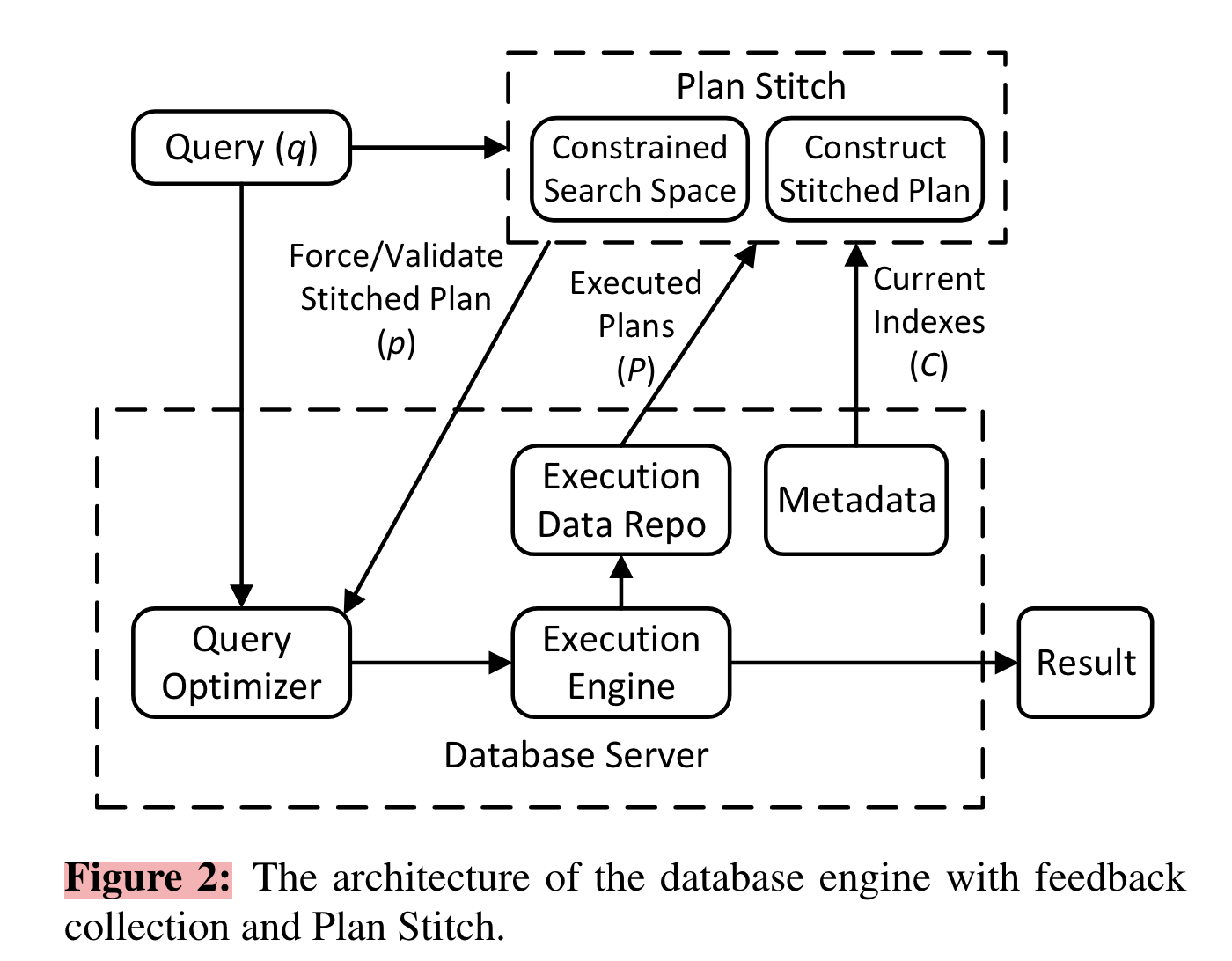
Plan Stitch 在查询优化和执行的关键路径之外工作,作为外部组件或者背景线程。
-
优化器为 给定的查询和现在的配置 选择一个计划,计划执行并且将执行时的统计信息被记录在仓库中。 执行的统计信息——计划结构和算子级别的执行代价。
-
仓库 主动收集计划的历史,包括同一个查询的已经执行的不同计划
-
当同一个查询的不同计划已经执行,并且执行信息在仓库中可用:触发 Plan Stitch 来查找可替代的 拼接计划。
3.1 触发后,Plan Stitch 从仓库中获得已执行计划,从 元数据 中获得现在的索引配置。
3.2 Plan stitch 将最终生成的缝合 plan 传给优化器,可以用于 查询 q 未来的执行。
4 Plan stitch 会用 强制特征系统 指定查询的执行计划暗示,使得优化器用此暗示来在计划搜索进行剪枝。
5 仓库会对查询执行计划进行超龄判断,以确保在数据变化时 Plan Stitch 代价估计的准确。
」
Plan Stitch(核心)
Constrained Search Space
“Constrained Search Space” (Ding 等, 2018, p. 1126) 「
生成受限搜索空间分两个步骤:
一、识别等价的子计划:
是否等效
- 逻辑表达式 相同
- 需要的物理属性 相同
之前的工作:
tests 和 greedy 算法
本文章的实现:
自己实现的关于匹配等效子计划的算法:
用类似于之前工作的启发式 提供在实现简易、开销和匹配的准确度中 的合理平衡。
用优化器来确保缝合计划的准确,以当作计划强制的副作用。
二、编码受限的搜索空间
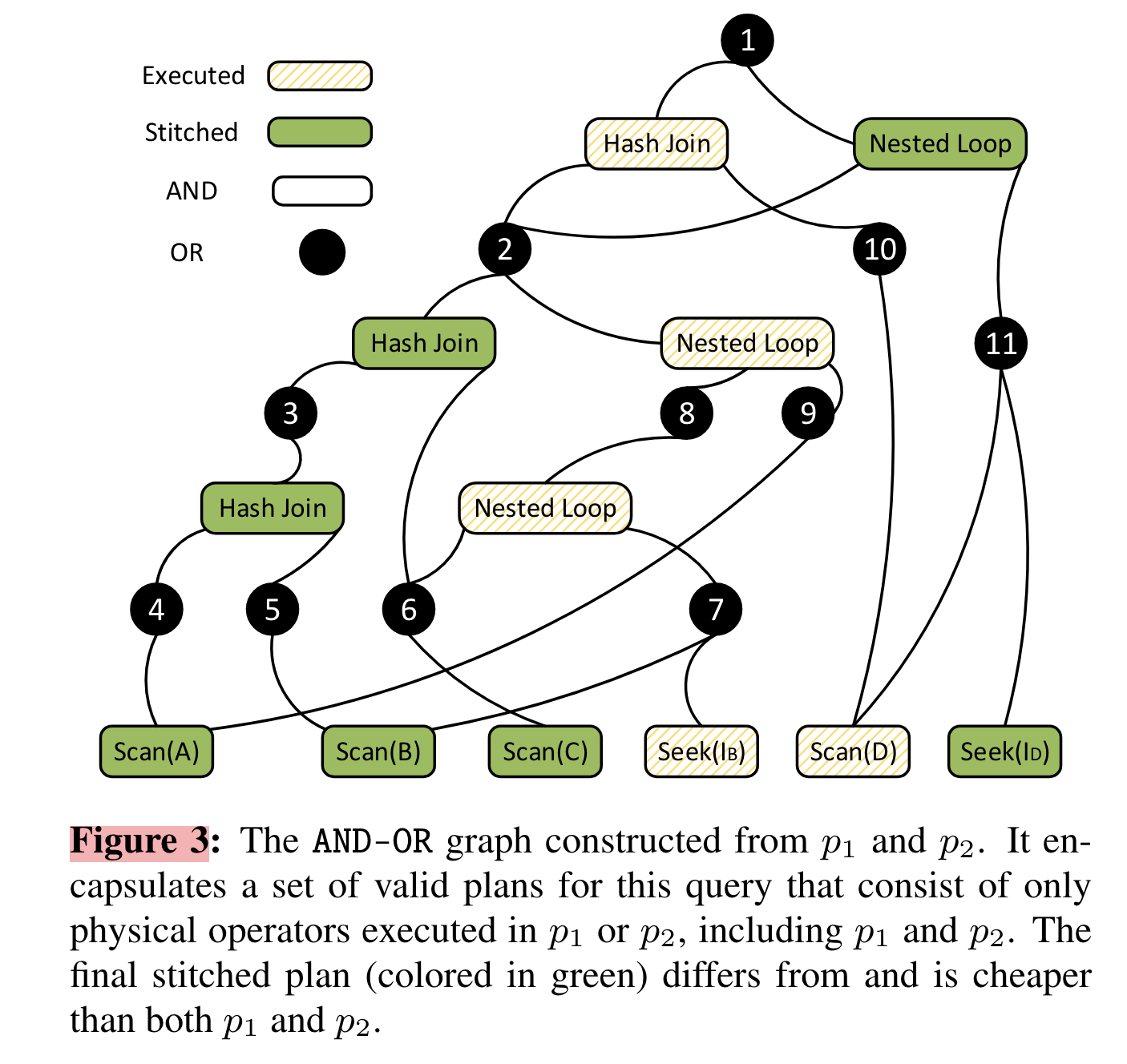
构造一个 AND-OR 图(参考Volcano 优化器生成器的文章?)。
- AND 节点对应 physical operator
- OR 节点对应 一个有着 physical properties 的 logical expression
为什么使用 AND-OR图:
-
一个AND节点的所有孩子节点一定是OR节点:OR 子节点 代表 AND 节点的孩子子计划对应的logical expr 和 所需 physical properties
-
一个OR节点的所有子节点一定是AND节点:AND 子节点代表 OR 节点对应 Logical Expression 的 可替代子计划的 根物理算子
具体构造过程:
- 首先,对于一个给定的查询,在它对应已执行的所有执行计划中,分别识别出每个以物理算子为根的子计划的所有等效子计划;
- 对于一个等效子计划组,创建一个 OR 节点来代表这个子计划组的逻辑表达式和需要的的物理属性;
- 对于这个组中每个子计划的物理算子,在该 OR 节点下分别创建子节点 AND。
」
Constructing the Stitched Plan
“Constructing the Stitched Plan” (Ding 等, 2018, p. 1126) 「
构建缝合计划:
AND-OR 图的两个性质:
- 无环图
- 至少有一个 OR 节点,代表该查询
概述:使用 动态规划 算法,从叶子 AND 节点到 根 OR 节点,为每一个 AND 节点 和 OR节点 缝合一个代价最低的缝合计划。
分情况获得最优缝合计划:
叶子层的最优缝合计划:就是 AND 节点自己
OR节点的最优缝合计划:从子 AND 节点中找到最低代价的缝合计划
非叶子AND节点的最优缝合计划:将其每个子OR节点的最优缝合子计划,缝合到 AND 节点对应的 物理算子下,当做一个一AND节点为根的缝合子计划
计算缝合计划的代价:
- 每个算子都存储着过去执行时的代价。通过比较代价来得到每个节点的最优缝合计划。
- 使用函数 stitchedSubUnitCost 来计算以op为根的缝合计划的代价。
」
Stitch ALgorithm
将算法1和图3结合起来可以很容易理解。
根据输入的 AND-OR 图,自底向上地利用动态规划算法实现 根OR节点 的最廉价缝合子计划。