本文来自我的洛谷博客。
本题解力求使用清晰易懂的图片和文字,讲解最简洁的道理。
请大家耐心地看完,注意要结合图片一起哦~~
2022-8-24 更改了格式与错别字
2022-8-28 更改了数学公式格式
这是本蒟蒻第一次写题解,不足之处请多包涵
题目大意:
读完题的可以跳过这一部分
给定一个矩阵,每个位置上都有数字。
可以分割 \(n-1\) 次,每次分割为2个矩形,然后把一半放在一旁,然后在另外一半继续割。
像这样:
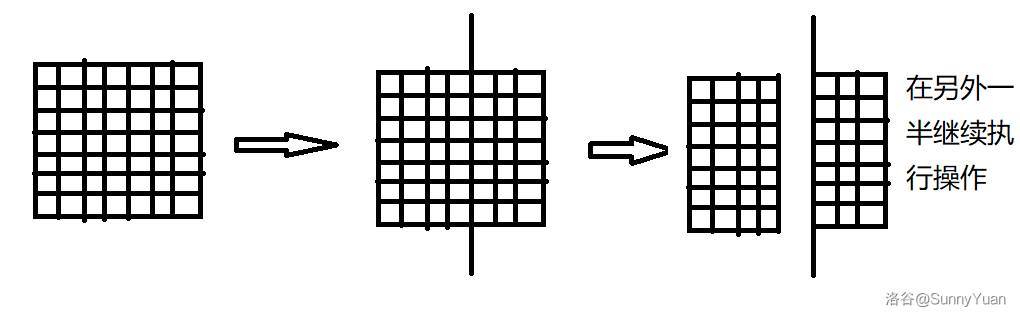
可以横切也可以纵切。
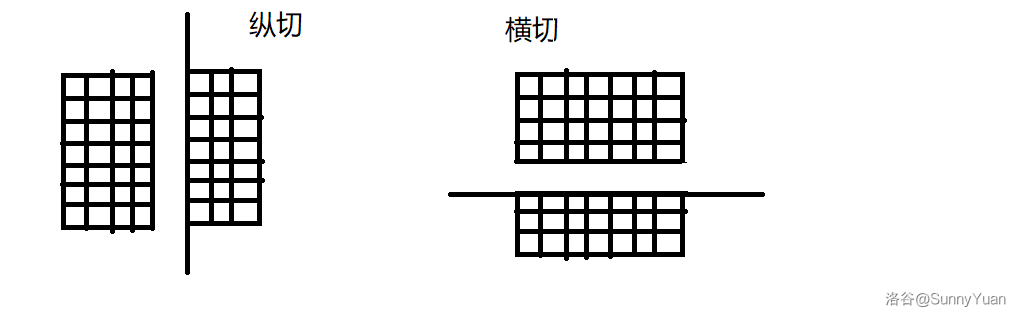
样例给的很好。
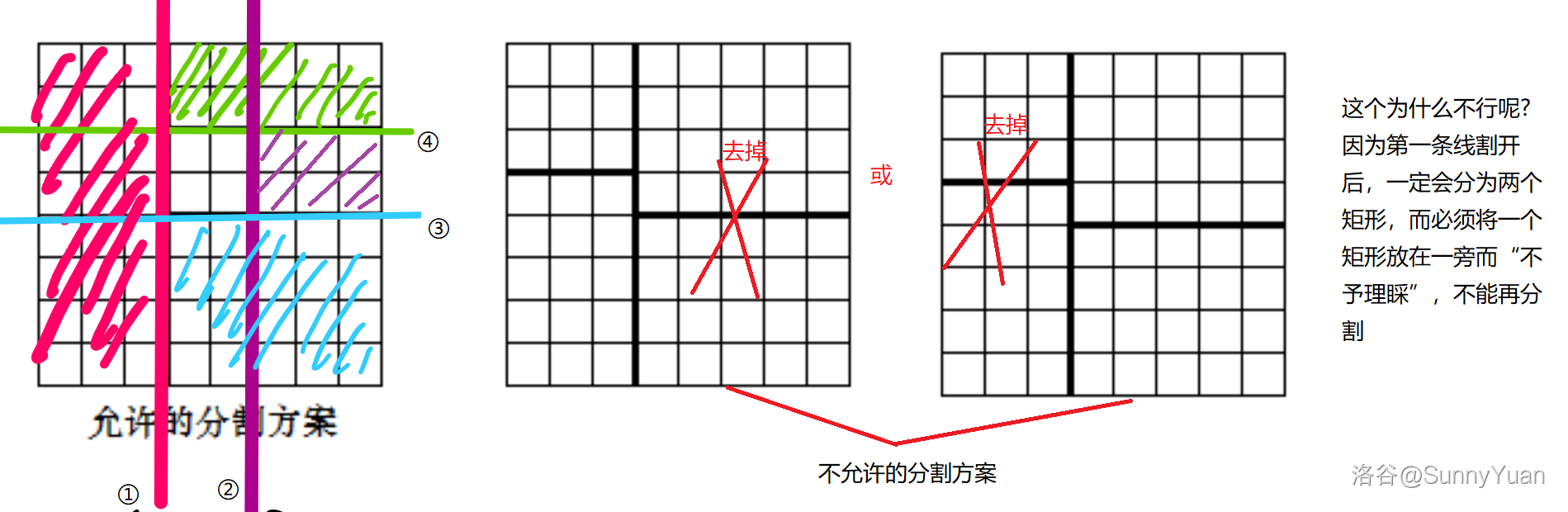
然后就分为 \(n\) 块(因为割了 \(n-1\) 次)。
记 \(X=s/n\) ,\(s\) 为矩阵中所有的数字之和。
设第 \(i\) 块的和为 \(x_i\) 那么求出怎样割才能使 \(\sum_\limits{i=1}^{n}(x_i-X)^2\) 更小。
分析问题:
我们看到这种分割问题,最后组合起来求总体最优值,便可以立马联想到区间DP。这叫望梅止渴做DP问题的复杂反射。
毕竟区间DP的主要思想就是大区间包含小区间,
小区间汇集成大区间。
好了,废话不多说,我们先从如下几个角度思考:
- 状态表示
- 状态含义
- 目标状态
- 状态转移
一、状态表示: \(f(x1,y1,x2,y2,k)\)
二、状态含义: \(f(x1,y1,x2,y2,k)\) 表示求解子矩阵 \((x1,y1)\) ~ \((x2,y2)\) 割了 \(k\) 刀得来的最优解(即下图框住区域的最优解)。
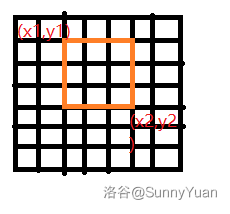
三、目标状态: \(f(1,1,8,8,n)\) 即求解整个矩阵被割了 \(n\) 刀的最优解。
四、状态转移:
我们以下图为例,讲解 \(f(x1,y1,x2,y2,k)\) 是如何被拆分的。
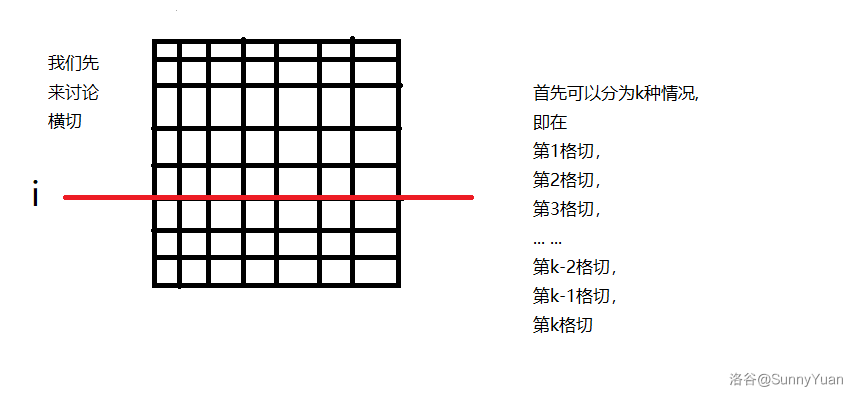
①:考虑选择上面继续割(如下图),丢掉下面的,其分界线为第i行。
所以应该取上面的最优值,同时少割一刀: \(f(x1,y1,i,y2,k-1)\) ,
而下面的部分为定值: \((sum-X)\times(sum-X)/n\) 。
\(sum\) 为下面的部分所有格子的和。
这两个部分合起来就是 \(f(x1,y1,x2,y2,k)\) 。

②:考虑选择下面继续割(如上图)。
上面部分的定值: \((sum-X)\times(sum-X)/n\) 。
下面的最优值: \(f(i+1,y1,x2,y2,k-1)\) 。
\(sum\) 为上面的部分所有格子的和。
下面考虑纵切。
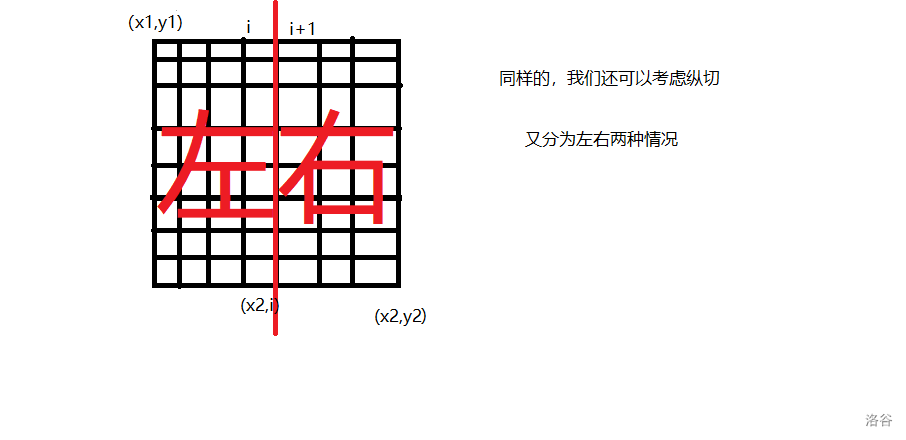
③:考虑选择左边继续割(如上图),分界线为第i列。
取左边的最优值: \(f(x1,y1,x2,i,k-1)\) ,
右边的部分为定值: \((sum-X)\times(sum-X)/n\) 。
\(sum\) 为右边的部分所有格子的和。
④:考虑选择右边继续割(如上图)。
取右边的最优值: \(f(x1,i+1,x2,y2,k-1)\) ,
左边的部分为定值: \((sum-X)\times(sum-X)/n\) 。
\(sum\) 为左边的部分所有格子的和。
我们每次取一个值,其实都是在将问题规模缩小。
情况考虑清楚了,那怎么从一个 \(f\) 到另一个 \(f\) 呢,如果是用普通的区间DP,那估计要使用5层甚至更多的循环,所以,我们使用万能的记忆化搜索
综上所述
我们便可以实现对大区间的拆分
而我们不断提到 \(sum\) ,是一块区域的和,那么,我们可以使用二维前缀和来维护。相信大家一定会
好了,上AC代码,也许代码可以解释许多问题
#include <bits/stdc++.h>
using namespace std;
const int N=15;
const double INF=1e10; //因为要求min,所以要定义INF
int n;
int m=8;
double X; //平均值
double s[N][N]; //记录每个格子的值
double f[N][N][N][N][N]; //状态
double GetSum(int x1,int y1,int x2,int y2)//求[x1,y1]~[x2,y2]的和,为下文的GetX服务
{
return s[x2][y2]-s[x1-1][y2]-s[x2][y1-1]+s[x1-1][y1-1];
}
double GetX(int x1,int y1,int x2,int y2)// 计算上文的(sum−X)×(sum−X)/n。
{
return (GetSum(x1,y1,x2,y2)-X)*(GetSum(x1,y1,x2,y2)-X)/n;
}
double DFS(int x1,int y1,int x2,int y2,int k)//使用记忆化搜索进行递归调用
{
double& v=f[x1][y1][x2][y2][k];//因为太难写了,所以给f[x1][y1][x2][y2][k]建立引用
if(v>=0)return v; //已经访问过该点了,直接返回
if(k==1)return v=GetX(x1,y1,x2,y2);//最后一块,不可能再割了
v=INF; //为求最小值做准备
for(int i=x1;i<x2;i++) //下面是刚刚讨论的结果
{
v=min(v,DFS(x1,y1,i,y2,k-1)+GetX(i+1,y1,x2,y2));
v=min(v,DFS(i+1,y1,x2,y2,k-1)+GetX(x1,y1,i,y2));
}
for(int i=y1;i<y2;i++)
{
v=min(v,DFS(x1,y1,x2,i,k-1)+GetX(x1,i+1,x2,y2));
v=min(v,DFS(x1,i+1,x2,y2,k-1)+GetX(x1,y1,x2,i));
}
return v;
}
int main()
{
scanf("%d",&n);
for(int i=1;i<=m;i++)
{
for(int j=1;j<=m;j++)
{
double x;
scanf("%lf",&x);
s[i][j]=s[i-1][j]+s[i][j-1]+x-s[i-1][j-1]; //建立前缀和
}
}
X=s[m][m]/n; //求平均值
memset(f,0x80,sizeof f); //初始化
printf("%.3f\n",sqrt(DFS(1,1,m,m,n)));//注意,一定要根号啊啊啊!!!
return 0;
}
码字不易,给个赞吧!
标签:P5752,y2,NOI1999,int,题解,sum,x2,y1,x1 From: https://www.cnblogs.com/PlayWithCPP/p/17202641.html