opengl除了基础的模型构建和贴图,还需要进行位置变换,缩放等功能,之前定义的顶点坐标(0,0.5,0),纹理坐标(0,0.5)实际上是一个向量,而对多个坐标构成的模型进行变换、缩放实际上是向量与矩阵相乘的结果,这涉及一些向量和矩阵的基础数学知识:
向量
Opengl只涉及三维,这里讨论的向量在一维到三维,三维向量如下:

向量的二维坐标,即z为0,向量的两个属性:大小和方向,通常默认(0,0,0)为初始点,一个向量为(1,2,3),即:自(0,0,0)出发,指向(1,2,3)点的一个向量(向量是有方向的,但是方向不影响向量的值),但是也可以自己定义出发点,比如从(0,0,1)为初始点,(1,2,3)为终点。
向量和标量的计算
标量,理解为一个数,1,3,5这都是标量,数学里是没有向量与标量的计算的,但是Opengl里的很多数学库都支持,举个例子:
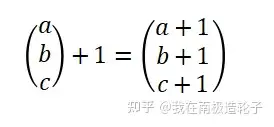
向量与标量的计算包括:加减乘除
向量的取反
向量的正负,只影响方向,对向量取反,即逆转方向
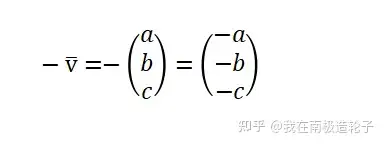
向量和向量的计算

向量和向量的计算包括:加减
向量的加法满足平行四边形法则和三角形法则,向量之间的计算实际上是向量的合成,以二维向量的计算为例,(2,1)+(1,3)=(3,4),实际上反应在图上是:
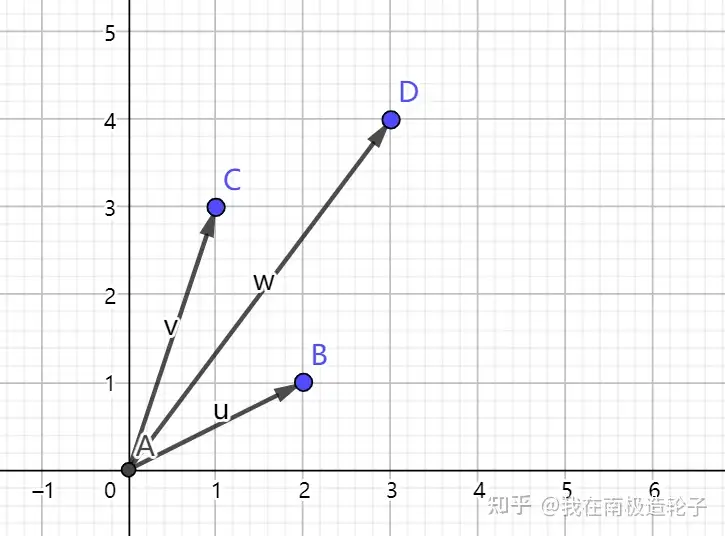
向量的长度
一个初始点为 (,,)(x1,y1,c1),终点为 (,,)(x2,y2,c2) 的向量,他的长度为 (a1−a2)2+(b1−b2)2+(c1−c2)2
向量的乘法
向量相乘,比较特殊的有点乘和叉乘
点乘,即向量的数乘结果乘以余弦值:
x1¯∗x2¯=||x¯1||∗||x¯2||∗cosθ
叉乘,是为了,在三维空间中,生成两个不平行向量的正交向量,正交简单理解即垂直。
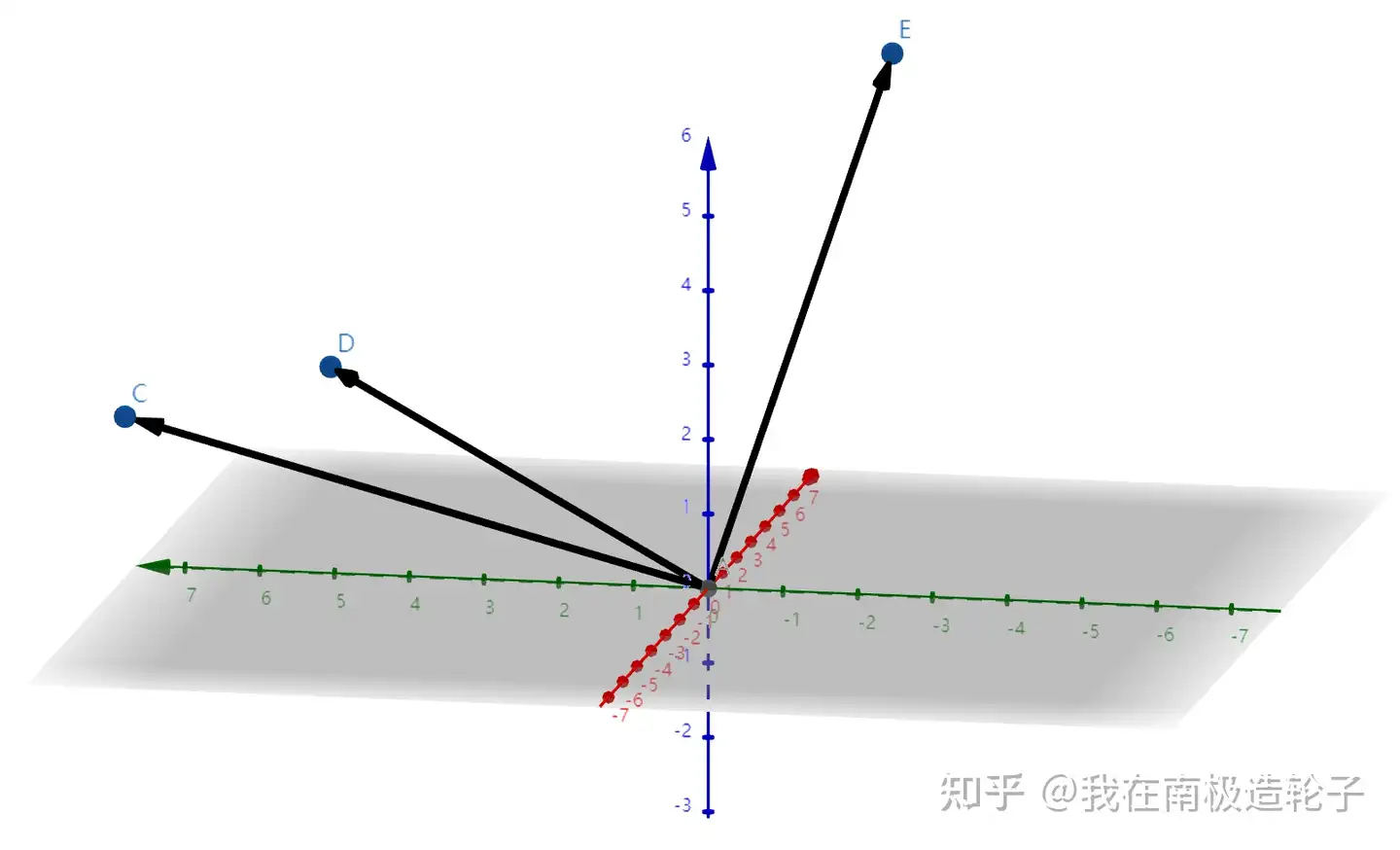
C、D是两个不平行的向量,两者进行叉乘获得向量E,向量E正交与B、D
叉乘计算公式:
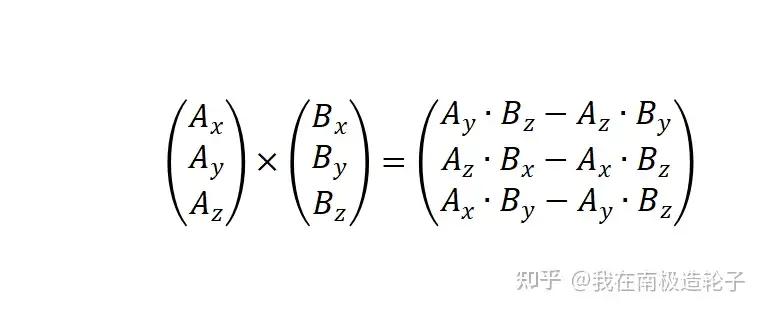
矩阵
矩阵就是一个矩形的数字、符号或表达式数组。矩阵中每一项叫做矩阵的元素(Element)。
一个2×2矩阵:

矩阵通过(i, j)进行索引,i是行,j是列
矩阵的计算
矩阵与标量的计算
即矩阵的每个元素对标量的计算,计算包括:加减乘除
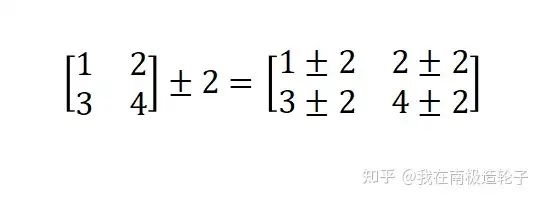
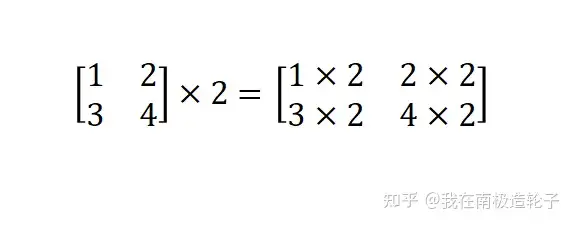
矩阵与矩阵的计算
矩阵与矩阵之间的加减,即矩阵元素之间的加减,通常的矩阵加法被定义在两个相同大小的矩阵。
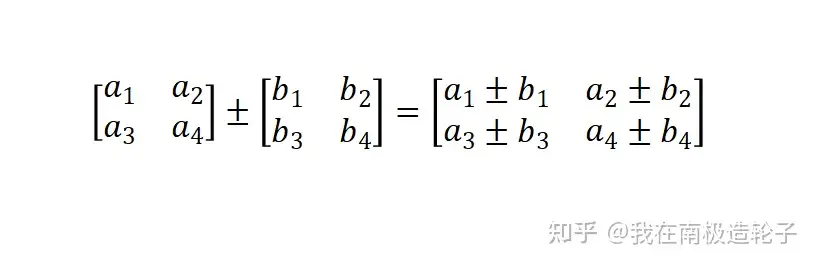
矩阵相乘需要遵循的规则:
- 只有当左侧矩阵的列数与右侧矩阵的行数相等,两个矩阵才能相乘。
- 矩阵相乘不遵守交换律,也就是说A⋅B≠B⋅A
矩阵的乘法是一系列乘法和加法组合的结果,它使用到了左侧矩阵的行和右侧矩阵的列,结果矩阵的第[1,1]元素:
a1∗b1+a2∗b4 即第一个矩阵的第一行 a1a2 乘以第二个矩阵的第一列 b1b4 ,同样第[1,2],即即第一个矩阵的第一行 a1a2 乘以第二个矩阵的第二列 b2b5 ...
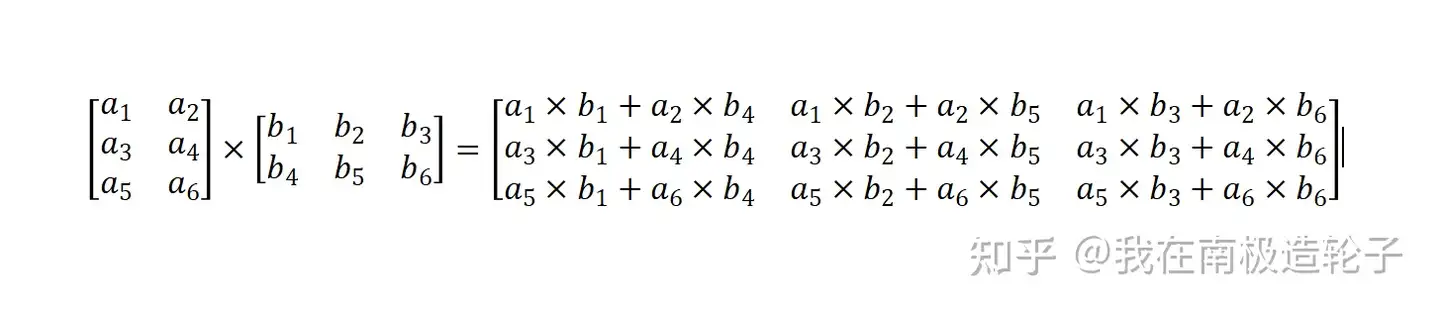
矩阵与向量
opengl里面定义的顶点坐标(0,0.5,0)是一个向量,它也是一个3*1的矩阵,形式如下:
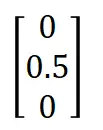
所以矩阵与向量的计算,实际上是矩阵与N*1矩阵的计算,按照之前矩阵相乘的定义,这个计算矩阵应该是个1*M或者M*N的格式(我们常用的是M*N,实际上,是N *N)
缩放、位移与旋转
模型的位置和体积都是顶点与矩阵的相乘
缩放
对于顶点与矩阵的计算实现缩放,可以参考这个例子
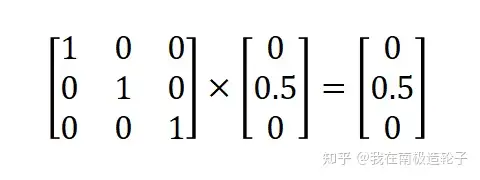
顶点,即向量(0,0.5,0)乘的为单位矩阵,计算结果不变,如果单位矩阵乘以0.5,再与向量相乘,向量结果将缩小一倍,如下
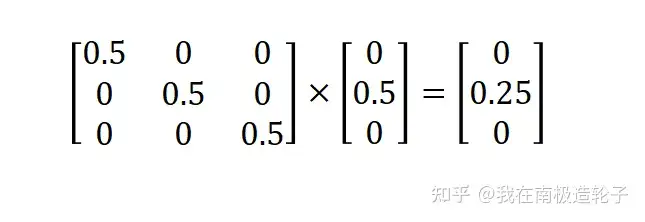
同样,如果所有顶点坐标都与以上的矩阵相乘,那么模型体积就能缩小一倍,这就是缩放。
位移
要实现顶点的位移,就是让顶点向量统一增加某个数,看起来就像是:

实现方式:
基于单位矩阵
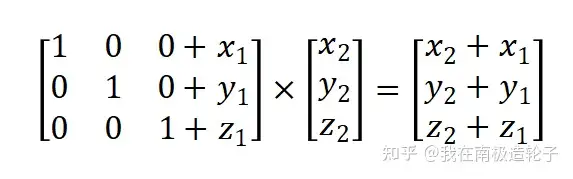
要移动 顶点x1y1z1的 x2y2z2 距离,就在单位矩阵最后一列的对应位置加上对应的距离。
这样定义的一个矩阵就是位移矩阵,有了位移矩阵我们就可以在3个方向(x、y、z)上移动物体,它是我们的变换工具箱中非常有用的一个变换矩阵。
旋转
向量的旋转,简单理解就是向量围绕一个轴,进行了 α 度的偏转,通常情况下是个三维空间,也就是旋转涉及x、y、z轴,与缩放、位移一样,需要乘以矩阵实现,因为涉及三个轴的旋转,所以不同的旋转需要乘以不同的矩阵,情况如下:
围绕x轴旋转pitch:α 度的偏转
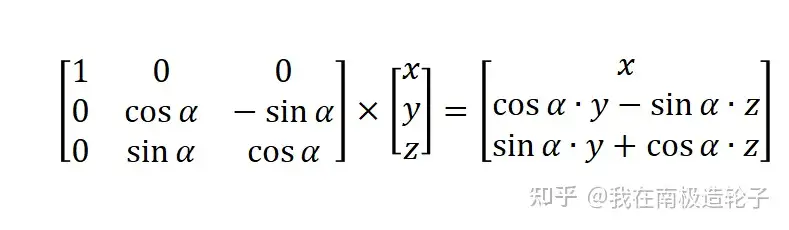
围绕y轴旋转Yaw: α 度的偏转
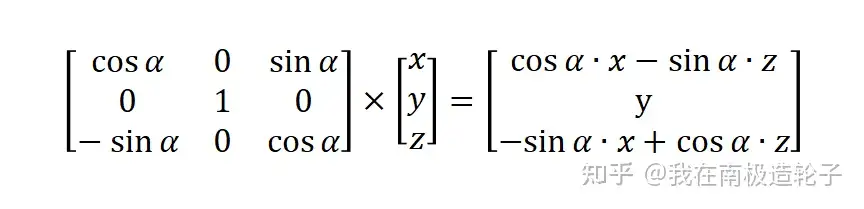
围绕z轴旋转Roll: α 度的偏转
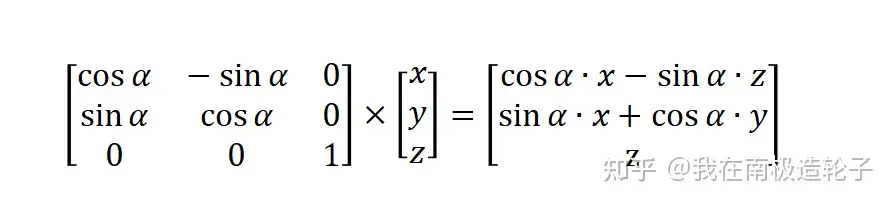
这里不解释这些矩阵是如何得到的,感兴趣的可以搜索下线性代数的相关知识,但是需要注意的是,以上实现的都是单次旋转,通常情况,需要多次旋转,比如先围绕x轴,再围绕y轴
这会导致万向节死锁问题,即当三个万向节其中两个的轴发生重合时,会失去一个自由度的情形。简单理解就是,当模型绕着x轴旋转90°后,它的z轴和y轴旋转就是同一个方向,产生了旋转死锁,采用矩阵旋转是无法避免万向节死锁问题,使用四元数可以避免,关于四元数是比较复杂的一种实现方式,作为入门,最好还是先理解矩阵,刚刚提到的万向节死锁问题,常常是因为将x、y、z轴多个旋转矩阵的多个步骤的复合导致的,当顶点 (x1,y1,z1) 需要旋转到某个位置,可以直接对照位置实现对应旋转轴 (xr,yr,zr) 的一次变换,实现方式如下:
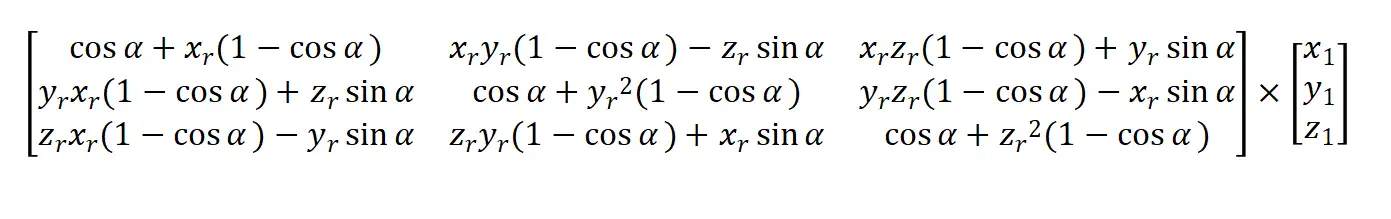
矩阵的组合
采用矩阵实现缩放、位移和旋转,一个很重要的因素在于,矩阵可以实现组合,例如:
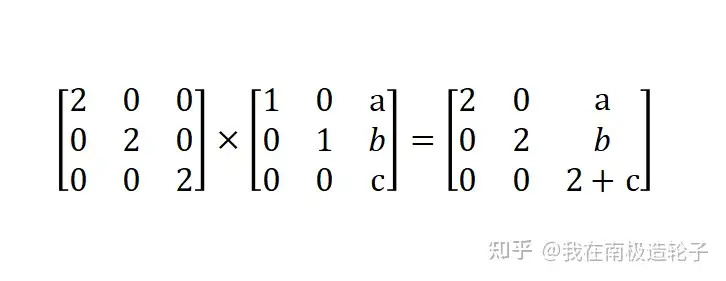
将顶点数据乘以上面组合后的矩阵,数据同时完成了放大两倍,平移(a,b,c)的位移。
https://zhuanlan.zhihu.com/p/484734712
标签:入门,Opengl,基础,缩放,矩阵,旋转,相乘,顶点,向量 From: https://www.cnblogs.com/im18620660608/p/17201340.html