自动机理论是计算理论中的一个重要的分支,其致力于建立抽象的计算模型来阐释计算,用抽象刻画出来的 “计算机” 来说明一些基本的计算问题,例如什么是可计算的(可计算性),计算的难度是什么样子的(计算复杂性),而 有穷状态机 \(\text{(finite state machine)}\) 是一类最基础,最简单的计算模型。
语言
语言是计算理论中一个很重要的概念,有穷状态机需要做的事情实际上即就是识别语言,而大多的抽象问题都可以编码为语言,那么解决问题即转化为识别语言。
定义 字母表 为任意一个非空有穷集合,用 \(\Sigma\) 表示,其中的元素为字母表中的符号,而 字母表上的字符串 为该字母表中符号的有穷序列,字符串的集合则称为 语言。
例如设 \(\Sigma_1=\{0,1\}\),则 \(01001\) 为 \(\Sigma_1\) 上的一个字符串,而 \(\{\varepsilon,0,1,0001,10\}\) 为 \(\Sigma_1\) 上的一个语言。其中 \(\varepsilon\) 表示空串,即长度为 \(0\) 的字符串。
语言的 正则运算 \(\text{(regular operation)}\) 是下面三种运算:
设 \(A,B\) 是两个语言,那么有
- 并:\(A\cup B=\{x|x\in A\text{ or } x\in B\}\)
- 连接:\(A\circ B=\{xy|x\in A\text{ and } y\in B\}\)
- 星号:\(A^{*}=\{x_1x_2\cdots x_k|k\geq 0\text{ and } x_i\in A\}\)
有穷状态机
有穷状态机也可以叫做有穷自动机,因为习惯下文中将用 “自动机” 来代指这类对象,具体分类依据上下文而定。
下图描述了一个有穷状态机 \(\mathrm{M}\):
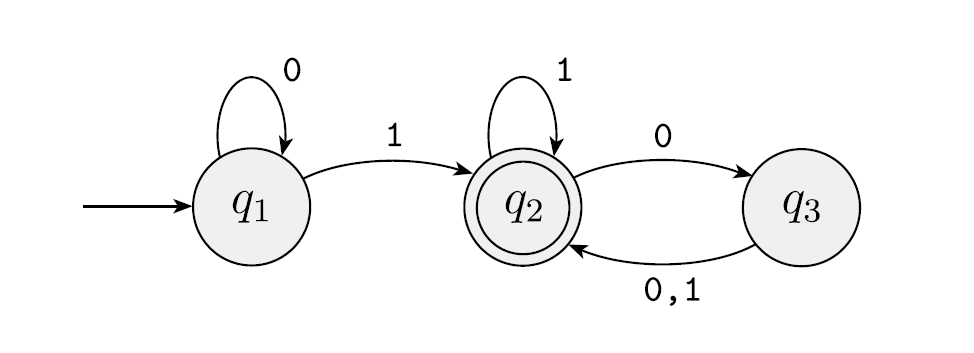
该图称为 \(\mathrm{M}\) 的 状态图,它有 \(3\) 个状态 \(q_1,q_2,q_3\),其中中 起始状态 \(q_1\) 用一个指向它的无出发点的箭头表示,接受状态 \(q_3\) 用双圈表示。状态之间用称为 转移 的箭头联系起来。
自动机以字符串为输入,它处理输入字符串并产生一个输出,表示为 接受 或 拒绝。它从左往右逐个接受输入字符串的所有符号,当输入一个符号时,它将沿着标有该符号的转移从一个状态移动到另一个状态,当输入最后一个符号时产生输出,如果自动机处于一个接受状态,输出为接受,否则为拒绝。
顺便一提,上图中的自动机接受所有至少含有一个 \(1\) 且在最后一个 \(1\) 后有偶数个 \(0\) 的字符串。
接下来我们将形式化地定义有穷自动机和在它上面的计算:
有穷自动机 是一个五元组 \(\mathrm{M}=(Q,\Sigma,\delta,q_0,F)\),其中
$1.\ $ \(Q\) 是一个有穷集合,称为 状态集。
$2.\ $ \(\Sigma\) 是一个有穷集合,称为 字母表。
$3.\ $ \(\delta:Q\times\Sigma\rightarrow Q\) 是 转移函数。
$4.\ $ \(q_0\in Q\) 是 起始状态。
$5.\ $ \(F\subseteq\) 是 接受状态集。
设 \(w=w_1w_2\cdots w_n\) 是一个字符串,如果存在 \(Q\) 中的状态序列 \(r_1,r_2,\cdots,r_n\) 满足下述条件:
$1.\ $ \(r_0=q_0\)
$2.\ $ \(\delta(r_i,w_{i+1})=r_{i+1}\) 对于 \(i=0,1,\cdots,n-1\)
$3.\ $ \(r_n\in F\)
则称 \(\mathrm{M}\) 接受 \(w\)。
称自动机 \(\mathrm{M}\) 接受的全部字符串集合 \(L\) 为 自动机 \(\mathrm{M}\) 的语言,或者说 \(\mathrm{M}\) 识别 \(L\)。对于一个自动机 \(\mathrm{M}\),这个 \(L\) 是唯一的。
例如前面图中的 \(\mathrm{M}\) 可以形式地写成 \(\mathrm{M}=\{Q,\Sigma,\delta,q_1,F\}\),其中 \(Q=\{q_1,q_2,q_3\}\),\(\Sigma=\{0,1\}\),起始状态为 \(q_1\),\(F=\{q_2\}\),\(\delta\) 描述为
| \(0\) | \(1\) | |
|---|---|---|
| \(q_1\) | \(q_1\) | \(q_2\) |
| \(q_2\) | \(q_3\) | \(q_2\) |
| \(q_3\) | \(q_2\) | \(q_2\) |
\(\mathrm{M}\) 的语言 \(L\) 为
\[L=\{w|w\text{ 至少含有一个 1 并且在最后一个 1 的后面有偶数个 0}\} \]非确定性
非确定型 计算是 确定型 计算的推广,在确定型计算中,机器每一步的计算都是按照唯一的转移法则,根据下一个输入的符号确定下一个状态。但是在非确定型计算中,转移法则不是唯一的。
有穷自动机也存在这两个种类,分别为 确定型有穷自动机 \(\text{(DFA)}\) 和 非确定型有穷自动机 \(\text{(NFA)}\)。上面的例子是一个 \(\text{DFA}\)。对于在 \(\text{NFA}\) 上的某个状态上的某个输入字符,我们会指定若干个转移的方式,甚至不指定对应的转移,机器会并行地执行所有分支,即使某一个分支由于不存在对应的转移而直接结束,整个计算也不会结束。最后,若存在一个分支在最后到达了一个接受状态,那么输出接受,否则输出拒绝。

接下来我们形式化地定义非确定型有穷自动机和在它上面的计算:
非确定型有穷自动机 是一个五元组 \(\mathrm{N}=\{Q,\Sigma_{\varepsilon},\delta,q_0,F\}\),其中
$1.\ $ \(Q\) 是有穷的状态集。
$2.\ $ \(\Sigma_{\varepsilon}\) 是有穷的字母表。
$3.\ $ \(\delta:Q\times\Sigma_{\varepsilon}\rightarrow \mathcal{P}(Q)\) 是转移函数,其中 \(\mathcal{P}(Q)\) 表示 \(Q\) 的所有子集组成的集合。
$4.\ $ \(q_0\in Q\) 是起始状态。
$5.\ $ \(F\subseteq\) 是接受状态集。
设 \(w=w_1w_2\cdots w_n\) 是一个字符串,如果存在 \(Q\) 中的状态序列 \(r_1,r_2,\cdots,r_n\) 满足下述条件:
$1.\ $ \(r_0=q_0\)
$2.\ $ \(r_{i+1}\in\delta(r_i,w_{i+1})\) 对于 \(i=0,1,\cdots,n-1\)
$3.\ $ \(r_n\in F\)
则称 \(\mathrm{N}\) 接受 \(w\)。
\(\text{NFA}\) 与 \(\text{DFA}\) 的计算能力
在自动机上进行的计算即为识别语言,那么它们识别语言的能力就代表了它们的计算能力。后面我们会讨论有穷自动机识别的语言类,即正则语言,为此这里我们先研究一下 \(\text{DFA}\) 和 \(\text{NFA}\) 的计算能力有何区别。
直觉上来说,\(\text{NFA}\) 的计算能力似乎比 \(\text{DFA}\) 更强,因为它可以并行计算,用更简单的状态来识别同样的语言。对于两台自动机识别同样的语言,那么称它们是 等价 的,令人惊奇地是,\(\text{NFA}\) 和 \(\text{DFA}\) 是等价的,即 每一台非确定型有穷自动机都等价于某一台确定型有穷自动机。
证明 设 \(\mathrm{N}=(Q,\Sigma,\delta,q_0,F)\) 为一台识别语言 \(A\) 的 \(\text{NFA}\),下面考虑构造一台识别语言 \(A\) 的 \(\text{DFA}\) \(\mathrm{M}=(Q',\Sigma,\delta',q_0',F')\)。
标签:语言,text,有穷,状态机,正则,自动机,Sigma,mathrm From: https://www.cnblogs.com/yukari1735/p/17149508.html