前言
线段树经常用来维护区间信息,支持单点修改、区间修改、单点查询、区间查询等操作。其中单点修改/查询其实可以类似地看成区间长度为 \(1\) 的区间。而上面的操作时间复杂度均为 \(O(\log n)\).
基本结构和建树
线段树是采用递归的思想来维护信息的,将每个长度不为 \(1\) 的区间划分为左右两个区间来递归求解,所以我们可以用二叉树来存储线段树,换言之,线段树就是一棵二叉树。而因为线段树是一棵二叉树,所以我们一般需要开 \(4\) 倍空间来存储数据。
例如有一个序列 \(A=\{1,3,4,2,5,6\}\),而我们要维护的信息是区间和,那么我们用线段树来存储就是类似于这样一个结构。
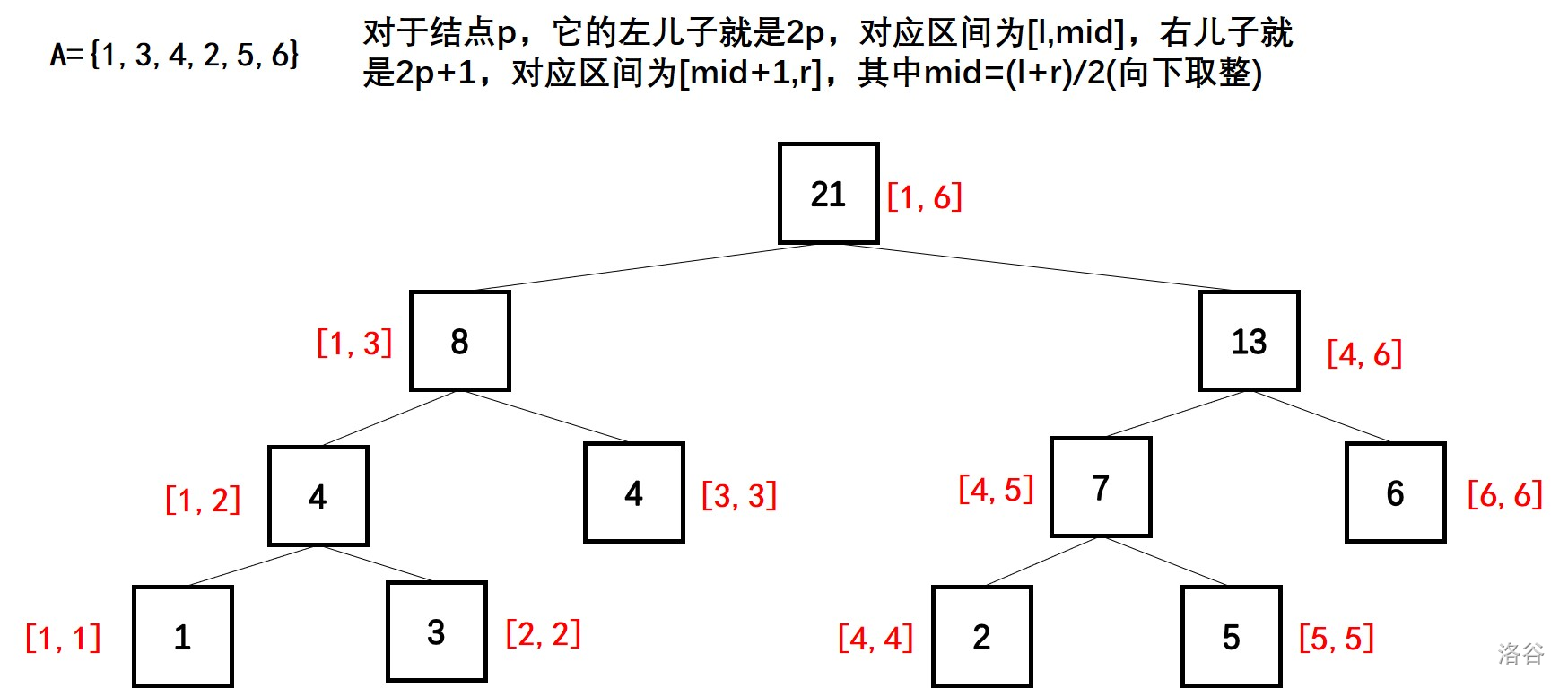
那么我们就可以考虑递归建树,从根节点开始,每次将结点所存储的区间划分为两个子区间,然后向下建树。
int a[N];//表示需存储的序列
struct node {
int l,r;//该节点的数据区间
int val;//该节点的值
}tr[N<<2];//N<<2等同于N*4
void push_up(int x) {
tr[x].val=tr[x<<1].val+tr[x<<1|1].val;//x<<1等同于x*2 x<<1|1等同于x*2+1
}
void build(int l,int r,int x) {//l,r表示当前区间,而x表示当前区间所属于的结点编号
tr[x].l=l;tr[x].r=r;
if(l==r) {//如果区间长度为1,直接赋值
tr[x].val=a[l];
return;
}
int mid=(l+((r-l)>>1));//l+((r-l)>>1)等同于(l+r)/2
build(l,mid,x<<1);//x<<1等同于x*2
build(mid+1,r,x<<1|1);//x<<1|1等同于x*2+1
push_up(x);//向上合并
}
单点修改
单点修改时我们就直接从根节点向下找到长度为 \(1\) 且包含这个位置的结点。例如上面的线段树,我们要将 \([3,3]\) 的值修改为 \(8\),那么我们就先从根节点开始找,一直递推下去直到找到区间 \([3,3]\) 的节点,然后修改该节点的值,接着再递归合并即可。
以上面这棵线段树为例,具体过程如下:
-
从根节点开始找,区间为 \([1,6]\),可发现左子树包含区间 \([1,3]\),于是向左子树找。
-
当前区间为 \([1,3]\),可见右子树包含区间,于是向右子树找。
-
当前区间为 \([3,3]\),已找到该区间,修改值。
-
向上递归为根节点,计算根节点的值。
-
继续递归到整颗线段树的根节点,然后修改值。
void update(int p,int k,int x) {//将a[p]的值更改为k,x表示当前查找结点
if(tr[x].l==p&&tr[x].r==p) {
tr[x].val=k;
return;
}
int mid=(l+((r-l)>>1));
if(p<=mid) update(p,k,x<<1);
else update(p,k,x<<1|1);
push_up(x);
}
单点查询
那么单点查询类似于单点修改,我们只要找到包含该结点的区间,且区间长度为 \(1\),然后直接返回该节点的值即可。
区间查询
当我们要求 \([l,r]\) 的区间和时,我们一样先从根节点开始找。先判断该区间是否完全包含当前节点的区间,如果是的话,我们直接返回该区间的值,如果不是,那么如果与左子树有交集,那么我们就向左子树递推,如果与右子树有交集,那么我们就向右子树递推。
我们以查询区间 \([3,6]\) 的区间和为例:
-
先从根节点开始查找,可见根节点的区间 \([1,6]\) 不被查询区间包含,那么我们就判断左子树,左子树与查询区间有交集,所以我们向左子树递推。
-
当前区间 \([1,3]\) 不被查询区间包含,那么我们就可以发现查询区间与左子树没有交集,但是与右子树有交集,所以我们向右子树递推,可以发现右子树区间 \([3,3]\) 被查询区间完全包含,那么我们就获取该区间的区间和,累加到答案中。至此,根节点的左子树就查找完毕。
-
我们继续判断根节点的右子树,可以发现根节点的右子树与查询区间是被完全包含的关系,所以我们直接返回右子树的区间和,累加到答案中。
-
我们将左右子树查找出来的答案合并起来,便是区间 \([3,6]\) 的和。
int query(int l,int r,int x) {//查询区间[l,r]的和,当前查找节点为x
if(l<=tr[x].l&&tr[x].r<=r) return tr[x].val;
int ans=0;
int mid=(tr[x].l+((tr[x].r-tr[x].l)>>1));
if(l<=mid) ans+=query(l,r,x<<1);
if(r>mid) ans+=query(l,r,x<<1|1);
return ans;
}
区间修改
我们如果要进行区间修改,很容易想到的做法就是像单点修改一样,将区间的每一个点都进行修改,那么这样就和暴力做法相差无几了。所以为了保证时间复杂度,我们就要引入懒标记。
顾名思义,懒标记就是一个标记,作用是来延迟操作。当我们需要时,我们在进行操作,不需要时只需要记录有这次操作的存在即可。这样可以大幅降低不必要的操作次数。
详细地说,就是我们只更改当前区间的值,而不更新区间包含的子区间的值,只是打上标记,当我们需要用到子区间时,再更新子区间的值。
我们在进行区间修改时遵循着以下的基本步骤:判断当前区间是否被完全包含于修改区间。如果包含,则直接修改当前结点的值,同时将该节点的懒标记进行更新,直接回溯。如果不包含,则类似于区间查询,向满足条件的左右子树递推。重复以上操作。要注意的是,在修改区间的值时,应当是修改的值与区间长度的乘积。
我们以将区间 \([3,5]\) 的值全部更改为 \(5\) 为例:
-
从根节点开始找,当前区间 \([1,6]\) 不被完全包含于修改区间中,经过判断发现,该左子树与修改区间有交集,于是向左子树递推。
-
可以发现当前区间 \([1,3]\) 不被完全包含于修改区间中,经过判断发现,该右子树与修改区间有交集,于是向右子树递推。可以发现右子树被完全包含于修改区间,所以我们修改当前节点的值为 \(5\times (3-3+1)=5\),并将当前节点懒标记的值修改为 \(5\).这样根节点的左子树就修改完毕。
-
可以发现根节点的右子树与修改区间有交集,于是我们向右子树递推。右子树并不被完全包含于修改区间,所以经过比较发现,当前区间的左子树与修改区间有交集,经过进一步比较发现,当前区间的左子树是被完全包含的关系,于是我们将当前区间的左子树的区间值修改为 \(5 \times (5-4+1)=10\),并将当前区间的懒标记的值修改为 \(5\).
-
这样区间修改就完毕了。
那么类似地,区间查询也只要加上一步下放标记即可。
struct node {
int l,r;//该节点的数据区间
int val;//该节点的值
int lazy;//懒标记
}tr[N<<2];//N<<2等同于N*4
void push_down(int x) {
if(tr[x].lazy) {
tr[x<<1].lazy=tr[x<<1|1].lazy=tr[x].lazy;
tr[x<<1].val=tr[x].lazy*(tr[x<<1].r-tr[x<<1].l+1);
tr[x<<1|1].val=tr[x].lazy*(tr[x<<1|1].r-tr[x<<1|1].l+1);
tr[x].lazy=0;
}
}
void update(int l,int r,int k,int x) {//将区间[l,r]的值更改为k,x表示当前查找结点
if(l<=tr[x].l&&tr[x].r<=r) {
tr[x].val=k*(tr[x].r-tr[x].l+1);
tr[x].lazy=k;
return;
}
push_down(x);
int mid=(tr[x].l+((tr[x].r-tr[x].l)>>1));
if(l<=mid) update(l,r,k,x<<1);
if(r>mid) update(l,r,k,x<<1|1);
push_up(x);
}
int query(int l,int r,int x) {//查询区间[l,r]的和,当前查找节点为x
if(l<=tr[x].l&&tr[x].r<=r) return tr[x].val;
int ans=0;
push_down(x);
int mid=(tr[x].l+((tr[x].r-tr[x].l)>>1));
if(l<=mid) ans+=query(l,r,x<<1);
if(r>mid) ans+=query(l,r,x<<1|1);
return ans;
}
总结
线段树可以维护区间和,区间乘积,区间最值等,其每次操作时间复杂度为 \(O(\log n)\).
例1:P3372
很明显,我们可以用一棵线段树来维护区间和,需要的操作有区间修改和区间查询。因为有 \(m\) 次操作,每次操作时间复杂度为 \(O(\log n)\),所以时间复杂度为 \(O(m \log n)\).
#include <cstdio>
#include <iostream>
using namespace std;
const int N=400005;
#define int long long
int n,m;
struct node {
int l,r;
int lazy,val;
}tr[N<<2];
int a[N];
void push_up(int p) {
tr[p].val=tr[p<<1].val+tr[p<<1|1].val;
}
void build(int l,int r,int p) {
tr[p].l=l;tr[p].r=r;
if(l==r) {
tr[p].val=a[l];
return;
}
int mid=l+((r-l)>>1);
build(l,mid,p<<1);
build(mid+1,r,p<<1|1);
push_up(p);
}
void push_down(int x) {
if(tr[x].lazy) {
tr[x<<1].lazy+=tr[x].lazy;
tr[x<<1|1].lazy+=tr[x].lazy;
tr[x<<1].val+=tr[x].lazy*(tr[x<<1].r-tr[x<<1].l+1);
tr[x<<1|1].val+=tr[x].lazy*(tr[x<<1|1].r-tr[x<<1|1].l+1);
tr[x].lazy=0;
}
}
void update(int l,int r,int k,int x) {
if(l<=tr[x].l&&tr[x].r<=r) {
tr[x].val+=k*(tr[x].r-tr[x].l+1);
tr[x].lazy+=k;
return;
}
push_down(x);
int mid=(tr[x].l+((tr[x].r-tr[x].l)>>1));
if(l<=mid) update(l,r,k,x<<1);
if(r>mid) update(l,r,k,x<<1|1);
push_up(x);
}
int query(int l,int r,int x) {
if(l<=tr[x].l&&tr[x].r<=r) return tr[x].val;
int ans=0;
push_down(x);
int mid=(tr[x].l+((tr[x].r-tr[x].l)>>1));
if(l<=mid) ans+=query(l,r,x<<1);
if(r>mid) ans+=query(l,r,x<<1|1);
return ans;
}
signed main() {
scanf("%lld%lld",&n,&m);
for(int i=1;i<=n;i++) scanf("%lld",&a[i]);
build(1,n,1);
int opt,x,y,k;
while(m--) {
scanf("%lld",&opt);
if(opt==1) {
scanf("%lld%lld%lld",&x,&y,&k);
update(x,y,k,1);
}
else {
scanf("%lld%lld",&x,&y);
printf("%lld\n",query(x,y,1));
}
}
return 0;
}
例2:P3373
这道题需要区间加和区间乘两种操作,那么只用一个懒标记是不行的,所以我们就需要两个懒标记,一个来记录加,一个来记录乘。
那么就有个问题,我们在 push_down 时要先加后乘,还是先乘后加。
我们注意到,如果先加后乘,那么结果就是 (val+add)*mul=val*mul+add*mul,而如果先乘后加,那么结果就是 val*mul+add,所以我们应当先乘后加,并且在下放标记时,懒标记中的 add 也应当相应的做乘法操作。
#include <cstdio>
#include <iostream>
using namespace std;
const int N=1e5+10;
struct node {
int l,r;
long long val,add,mul;
}tr[N<<2];
int n,m,mod;
int a[N];
void push_up(int p) {
tr[p].val=(tr[p<<1].val+tr[p<<1|1].val)%mod;
}
void push_down(int p) {
tr[p<<1].val=((tr[p<<1].val*tr[p].mul)%mod+((tr[p<<1].r-tr[p<<1].l+1)*tr[p].add)%mod)%mod;
tr[p<<1|1].val=((tr[p<<1|1].val*tr[p].mul)%mod+((tr[p<<1|1].r-tr[p<<1|1].l+1)*tr[p].add)%mod)%mod;
tr[p<<1].mul=(tr[p].mul*tr[p<<1].mul)%mod;
tr[p<<1|1].mul=(tr[p].mul*tr[p<<1|1].mul)%mod;
tr[p<<1].add=(tr[p].mul*tr[p<<1].add+tr[p].add)%mod;
tr[p<<1|1].add=(tr[p].mul*tr[p<<1|1].add+tr[p].add)%mod;
tr[p].add=0;
tr[p].mul=1;
}
void build(int p,int l,int r) {
tr[p].l=l;
tr[p].r=r;
tr[p].mul=1;
if(l==r) {
tr[p].val=a[l]%mod;
// printf("%d %d %lld\n",l,r,tr[p].val);
return;
}
int mid=l+((r-l)>>1);
build(p<<1,l,mid);
build(p<<1|1,mid+1,r);
push_up(p);
// printf("%d %d %lld\n",l,r,tr[p].val);
}
void change_mul(int p,int l,int r,int k) {
if(l<=tr[p].l&&tr[p].r<=r) {
tr[p].add=(tr[p].add*k)%mod;
tr[p].mul=(tr[p].mul*k)%mod;
tr[p].val=(tr[p].val*k)%mod;
return;
}
push_down(p);
int mid=tr[p].l+((tr[p].r-tr[p].l)>>1);
if(l<=mid) change_mul(p<<1,l,r,k);
if(r>mid) change_mul(p<<1|1,l,r,k);
push_up(p);
}
void change_add(int p,int l,int r,int k) {
// printf("%d %d\n",tr[p].l,tr[p].r);
if(l<=tr[p].l&&tr[p].r<=r) {
tr[p].add=(tr[p].add+k)%mod;
tr[p].val=(tr[p].val+k*(tr[p].r-tr[p].l+1))%mod;
return;
}
push_down(p);
int mid=tr[p].l+((tr[p].r-tr[p].l)>>1);
if(l<=mid) change_add(p<<1,l,r,k);
if(r>mid) change_add(p<<1|1,l,r,k);
push_up(p);
}
long long query(int p,int l,int r) {
if(l<=tr[p].l&&tr[p].r<=r) return tr[p].val;
push_down(p);
long long res=0;
int mid=tr[p].l+((tr[p].r-tr[p].l)>>1);
if(l<=mid) res=(res+query(p<<1,l,r))%mod;
if(r>mid) res=(res+query(p<<1|1,l,r))%mod;
return res;
}
int main() {
scanf("%d%d%d",&n,&m,&mod);
for(int i=1;i<=n;i++) scanf("%d",&a[i]);
build(1,1,n);
// printf("%lld\n",query(1,1,n));
// for(int i=1;i<=n;i++) printf("%lld ",query(1,i,i));
// puts("");
int opt,x,y,k;
while(m--) {
scanf("%d%d%d",&opt,&x,&y);
if(opt==1) {
scanf("%d",&k);
change_mul(1,x,y,k);
} else if(opt==2) {
scanf("%d",&k);
change_add(1,x,y,k);
} else if(opt==3) {
printf("%lld\n",query(1,x,y));
}
}
return 0;
}