问题提出
存在的问题
基于minimum snap生成的轨迹,我们控制的是waypoint,但是在轨迹生成的时候可能出现“overshoot”的现象,产生碰撞。
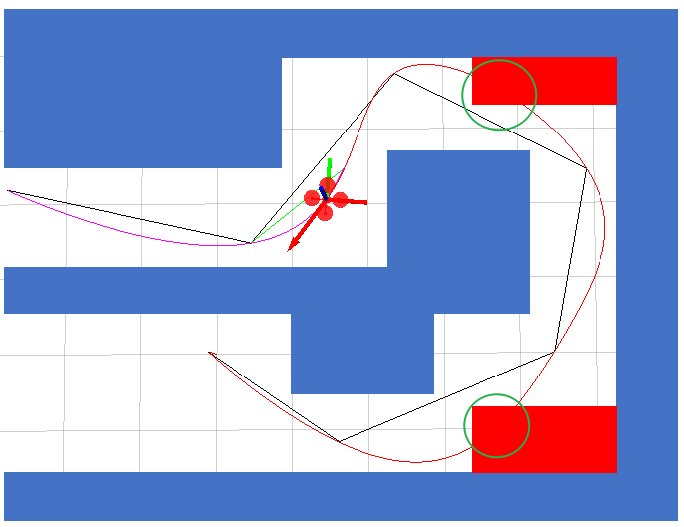
解决思路
- 在障碍物上加”推力“
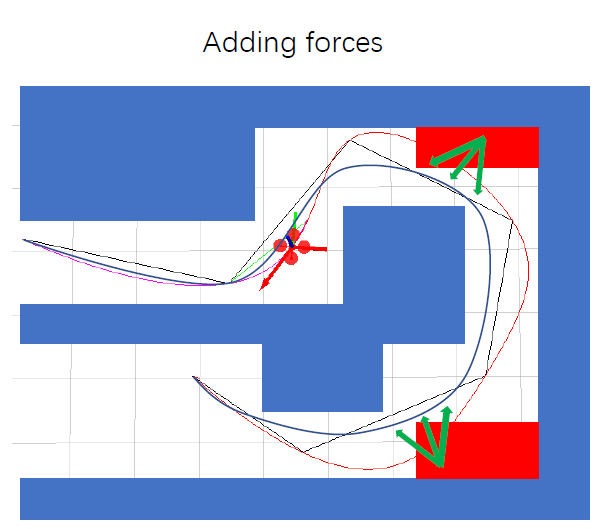
- 在可通行区域加约束
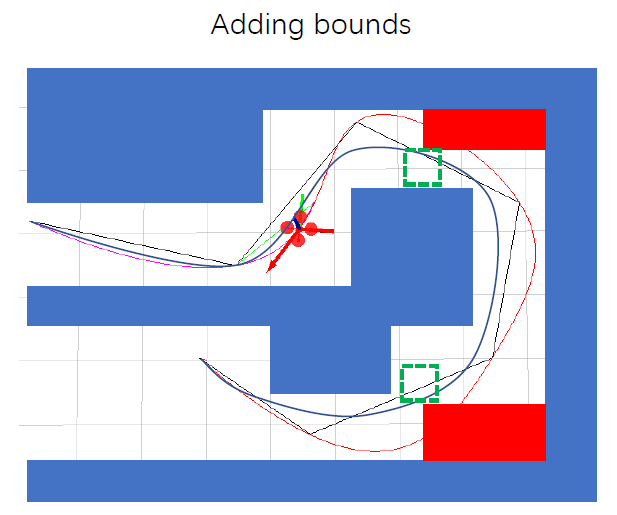
通常将第一种情况变成【软约束】的优化问题,将第二种情况变成【硬约束】的优化问题
硬/软约束的概念
- 硬约束
在整个x的定义域内,都要【严格满足等式约束和不等式约束】
\[\begin{matrix}\min&\quad f\left(x\right)\\ s.f.&\quad g_i\left(x\right)=c_i,\quad i=1,\cdots,n\quad\text{Equality constants}\\ &\quad h_j\left(x\right)\ge d_j,\quad j=1,\cdots,n\quad\text{ bluequality constraints}\end{matrix} \]- 软约束
将等式约束和不等式约束融入了目标函数中
\[\text{min}\quad f(x)+\lambda_1\cdot g(x)+\lambda_2\cdot h(x) \]使结果倾向于满足约束条件,而不是严格被满足,\(\lambda_1\cdot g(x)+\lambda_2\cdot h(x)\)被称为惩罚项/损失函数(loss function),有很多种常见的loss function,比如:
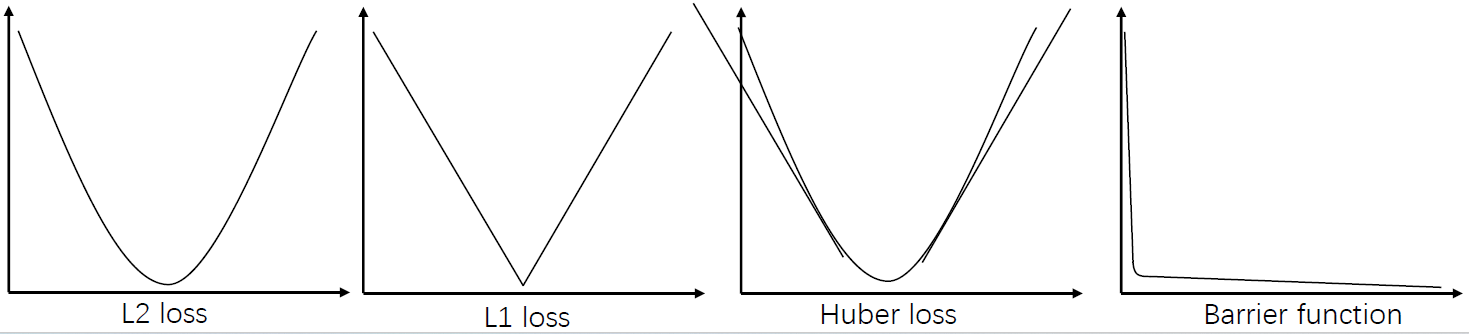
硬约束
Corridor based Trajectory Optimization
框架
- 将环境信息载入八叉树地图
- 用path-finding的方法,在地图上搜索出一条安全的路径(安全走廊)
- 将安全走廊在地图中进行膨胀
- 在膨胀后的安全走廊中进行轨迹生成
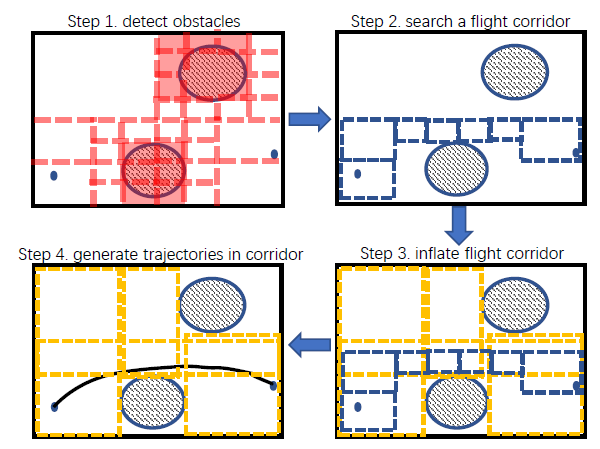
轨迹生成
- 分段多项式轨迹函数与minimum snap和minimum jerk是一样的:
- 优化的目标函数也是一样的
- 约束条件有所不同
由于我们是在安全走廊里进行优化的,并没有指定waypoint,因此waypoint的导数约束是没有的,取而代之的是安全性约束,具体的约束有:
- Instant linear constraints::
起点和终点的状态约束(\(Ap=b\))
Transition point 的约束(\(Ap=b,Ap≤b\))
我们希望在每个凸包内生成的轨迹都是被bound在凸包内的,但是这是一件比较困难的事情,可以先这样做,将分段的轨迹的连接点(Transition point),bound在两个凸包的公共区域内。
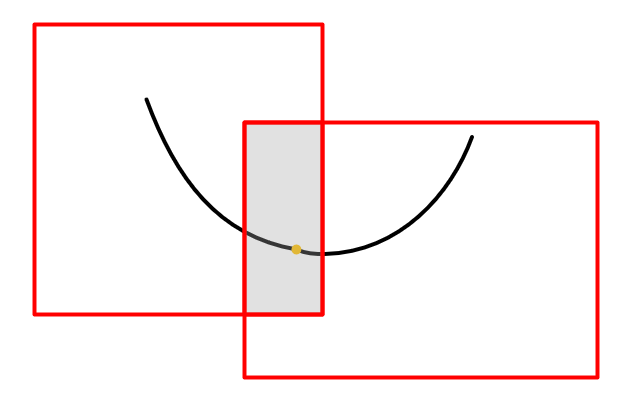
但是这样做也是不够的,轨迹也可能落在凸包外面,安全性不完备
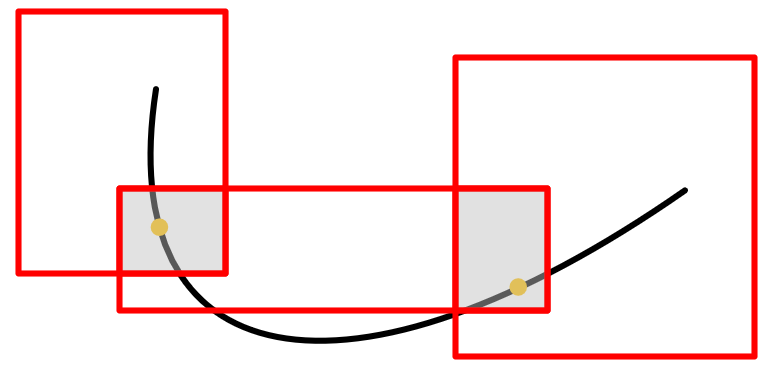
连续性约束(\(Ap_i=b_i\))
- Interval linear constraints:
边界约束(\(\textbf{A}(t)\textbf{p}\leq\textbf{b},\forall t\in[t_l,t_r]\)),整条轨迹的边界约束是很难施加的,除非将T离散化非常细,然后进行约束,但是这样会大大增加凸优化问题的约束数量,导致求解非常困难,通常采取后验的方式
动力学约束(\(\textbf{A}(t)\textbf{p}\leq\textbf{b},\forall t\in[t_l,t_r]\)),和边界约束同样的问题,难以施加,通常采取后验的方式
- 优点:效率非常高,质量非常高,由于没有了waypoint这种fixed的点,优化的自由度被大大增加了,能够自动找到最优的Transition point,而且可以隐式的调节时间分配的问题,在fixed的waypoint的时候如果T分配不好,得到的轨迹也不是很好,而现在point是可以在凸包交集里动的,因此可以隐式的调节时间分配带来的影响
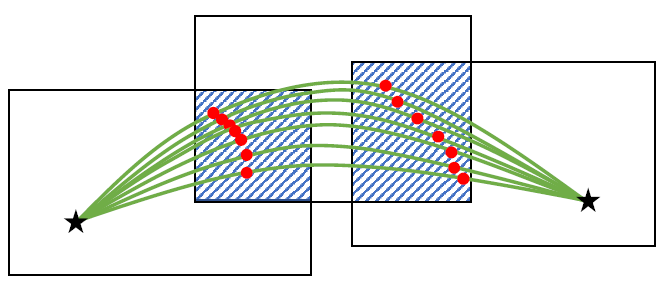
- 问题,全局边界和动力学的interval的约束是很难施加的
- 解决方法:
在轨迹生成之后做检查,不需要将t离散化逐个检查,检查极值即可,如果超过边界,继续施加新的约束,将极值往下压,可以收紧一些约束,然后迭代检查,约束,求解,需要多次求解QP,对在线求解速度施加了压力,而且有没有解,都需要进行多次迭代才能看出。
Bezier Curve Optimization
从普通多项式曲线转到贝塞尔曲线
用Bernstein polynomial代替monomial polynomial,贝塞尔曲线
\[\begin{array}{c}{{B_{j}(t)=c_{j}^{0}b_{n}^{0}(t)+c_{j}^{1}b_{n}^{1}(t)+\cdots+c_{j}^{n}b_{n}^{n}(t)=\sum_{i=0}^{n}c_{j}^{i}b_{n}^{i}(t)}}\\ {{b_{n}^{i}(t)={\binom{n}{i}}\cdot t^{i}\cdot(1-t)^{n-i}}}\end{array} \]monomial polynomial各阶的系数和Bernstein polynomial各阶系数是一一对应的,\(p = M c\)
\[For 6 order: \mathbf{M}=\left[\begin{array}{ccccccc}1 & 0 & 0 & 0 & 0 & 0 & 0 \\-6 & 6 & 0 & 0 & 0 & 0 & 0 \\15 & -30 & 15 & 0 & 0 & 0 & 0 \\-20 & 60 & -60 & 20 & 0 & 0 & 0 \\15 & -60 & 90 & -60 & 15 & 0 & 0 \\-6 & 30 & -60 & 60 & -30 & 6 & 0 \\1 & -6 & 15 & -20 & 15 & -6 & 1\end{array}\right] \]