经典老题
A. [CQOI2009] 中位数
题意
给出 \(1,2,\dots,n\) 的一个排列,统计该排列有多少个长度为奇数的连续子串的中位数是 \(b\)。
对于 \(100\%\) 的数据,满足 \(n\le100000,1\le b\le n\)。
思路
首先在输入的时候记录一下 \(b\) 在排列中的位置 \(pos\)。
然后发现要找的子串一定是包含 \(b\) 的,所以从 \(pos\) 分别往左右找。
对于一个满足条件的子串,大于 \(b\) 的数的个数一定等于小于 \(b\) 的数的个数。
在分别往左右找的过程中,设当前比 \(b\) 大的数的个数为 \(cnt1\),比 \(b\) 小的数的个数为 \(cnt2\)。
那么要找的子串一定满足:左边的 \(cnt1-cnt2\) 一定等于右边的 \(cnt2-cnt1\)。
于是在左边时用数组 \(a\) 记录一下 \(cnt1-cnt2\) 的位置数量 \(a[cnt1-cnt2]\),查找完清空 \(cnt1\) 和 \(cnt2\),在右边时答案加上每一位的 \(a[cnt2-cnt1]\) 即可(乘法原理?)。
数组下标可能有负数,但绝对值不超过 \(n/2\),于是令下标右移 \(n_{\max}/2=50000\)。
非常的暴力。
代码
#include <cstdio>
#include <iostream>
#define f(x, y, z) for (int x = (y); x <= (z); ++x)
#define g(x, y, z) for (int x = (y); x >= (z); --x)
#define FILENAME "median"
using namespace std;
int const N = 1e5 + 10;
int const BASE = 5e4;
int n, a[N], b, ans, pos, delta[N];
signed main() {
ios::sync_with_stdio(false);
cin.tie(0), cout.tie(0);
// freopen(FILENAME".in", "r", stdin);
// freopen(FILENAME".out", "w", stdout);
cin >> n >> b;
f(t, 1, n) {
cin >> a[t];
if (a[t] == b) pos = t;
}
int cnt1 = 0, cnt2 = 0;
delta[BASE] = 1;
g(i, pos - 1, 1) {
if (a[i] < a[pos]) ++cnt1;
else ++cnt2;
++delta[cnt1 - cnt2 + BASE];
}
cnt1 = cnt2 = 0;
f(i, pos + 1, n) {
if (a[i] < a[pos]) ++cnt1;
else ++cnt2;
ans += delta[cnt2 - cnt1 + BASE];
}
cout << ans + delta[BASE] << '\n';
return 0;
}
B. [HNOI2004] 敲砖块(朴素 DP)
题意
在一个凹槽中放置了 \(n\) 层砖块,最上面的一层有 \(n\) 块砖,从上到下每层依次减少一块砖。每块砖都有一个分值,敲掉这块砖就能得到相应的分值,如下图所示:
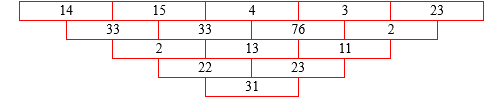
如果你想敲掉第 \(i\) 层的第 \(j\) 块砖的话,若 \(i=1\),你可以直接敲掉它;若 \(i>1\),则你必须先敲掉第 \(i-1\) 层的第 \(j\) 和第 \(j+1\) 块砖。
你现在可以敲掉最多 \(m\) 块砖,求得分最多能有多少。
对于 \(100\%\) 的数据,满足 \(1\leq n\leq 50\),\(1\leq m\leq \dfrac{n\times(n+1)}{2}\)。
思路
设 \(f(j,i,k)\) 表示将第 \(i\) 行第 \(j\) 列的砖敲掉,且当前一共已经敲掉 \(k\) 块砖的最大得分。
根据题意,要想敲掉第 \(j\) 列第 \(i\) 行砖,该列的第 \(1\sim i-1\) 行的砖一定都已经被敲掉了。
而第 \(j+1\) 列则 至少 敲掉了 \(i-1\) 行砖(至多敲掉了 \(n-j\) 行因为一共就这么多)。
现在我们想办法将第 \(j+1\) 列的状态转移到第 \(j\) 列。
枚举第 \(j\) 行敲的砖数 \(i\),然后枚举第 \(j+1\) 行敲的砖数 \(t\),于是写出了方程:
\[f(j,i,k)=\max_{i-1\le t\le n-j}\left\{f(j+1,t,k-i)\right\}+\sum_{l=1}^ia[l,j]. \]时间复杂度 \(O(n^3m)\),空间复杂度 \(O(n^2m)\),可以通过。
代码
#include <cstdio>
#include <cstring>
#include <iostream>
#define f(x, y, z) for (int x = (y); (x) <= (z); ++(x))
#define g(x, y, z) for (int x = (y); (x) >= (z); --(x))
#define FILENAME "brike"
using namespace std;
int const N = 55, M = 1255;
int const INF = 0x3f3f3f3f;
int n, m, a[N][N], f[N][N][M];
signed main() {
ios::sync_with_stdio(false);
cin.tie(0), cout.tie(0);
// freopen(FILENAME".in", "r", stdin);
// freopen(FILENAME".out", "w", stdout);
cin >> n >> m;
f(i, 1, n) f(j, 1, n - i + 1) cin >> a[i][j];
memset(f, 0xc0, sizeof f);
f[n + 1][0][0] = 0;
g(j, n, 1) {
int sum = 0;
f(i, 0, n - j + 1) {
sum += a[i][j];
f(k, i, m) {
int &tmp = f[j][i][k];
f(t, i ? i - 1 : 0, n - j)
tmp = max(tmp, f[j + 1][t][k - i] + sum);
}
}
}
int ans = -INF;
f(i, 1, n) f(j, 1, n - i + 1) ans = max(ans, f[i][j][m]);
cout << ans << '\n';
return 0;
}
C. 最小密度路径(魔改 Floyd)
题意
给出一张有 \(N\) 个点 \(M\) 条边的加权有向无环图,接下来有 \(Q\) 个询问,每个询问包括 \(2\) 个节点 \(X\) 和 \(Y\),要求算出从 \(X\) 到 \(Y\) 的一条路径,使得密度最小(密度的定义为,路径上边的权值和除以边的数量)。
\(1 \le N \le 50\),\(1 \le M \le 1000\),\(1\le W \le 10^5\),\(1 \le Q \le 10^5\)。
思路
首先发现 \(Q\) 很可能大于总有序点对数 \(N\times(N-1)\),所以直接预处理出所有点对的答案。
如果边数一定,那么问题就变成了纯纯的最短路问题。于是尝试枚举边数。
设 \(d(i,j,l)\) 表示从 \(i\) 到 \(j\) 经过边数为 \(l\) 的路径的最小边权和。
也就是说,我们在 Floyd 算法中的最短路上又附加了一维信息——边数。
枚举中间点 \(k\),枚举 \(i\) 和 \(j\),然后枚举从 \(i\) 到 \(j\) 的边数 \(l\),并且枚举从 \(i\) 到 \(k\) 的边数 \(t\)(那么从 \(k\) 到 \(j\) 的边数为 \(l-t\)),那么转移方程为
\[f(i,j,l)=\min\{f(i,k,t)+f(k,j,l-t)\}. \]然而我们发现时间复杂度为 \(O(N^3M^2)\),无法通过。考虑重复决策出现在哪里。
对于这样一条路径:\(i\to\dots\to k\to\dots\to b\to j\),假设用路径 \((i,k)\) 和路径 \((k,j)\) 可以更新路径 \((i,j)\) 的答案,那么路径 \((i,b)\) 和路径 \((b,j)\) 同样也可以更新。并且由于我们枚举了所有的中间点 \(k\),那么一定会枚举到 \(k=b\)。于是只需要令 \(t=1\) 来更新就可以了(事实上令 \(t\) 等于什么都行,不过要保证合法)。即
\[f(i,j,l)=\min\{f(i,k,1)+f(k,j,l-1)\}. \]于是复杂度就神奇地优化成了 \(O(N^3M)\)。
答案:\(\min\limits_{l\le n-1}\left\{\dfrac{f(x,y,l)}l\right\}\)。
初值:对于不合法的状态(即 \(i\) 无法到达 \(j\)),我们令数组初值全部为 \(+\infty\) 即可。对于每一条权值为 \(w\) 的有向边 \((s,t)\),令初值 \(f(s,t,1)=w\)。
代码
#include <cstdio>
#include <iomanip>
#include <cstring>
#include <iostream>
#define f(x, y, z) for (int x = (y); (x) <= (z); ++(x))
#define FILENAME "path"
using namespace std;
typedef double db;
int const N = 55, M = 1010;
int const INF = 0x3f3f3f3f;
int n, m, q, d[N][N][M];
db ans;
inline void getmin(int &p, int const &q) { p = min(p, q); }
signed main() {
ios::sync_with_stdio(false);
cin.tie(0), cout.tie(0);
// freopen(FILENAME".in", "r", stdin);
// freopen(FILENAME".out", "w", stdout);
cin >> n >> m;
memset(d, 0x3f, sizeof d);
f(i, 1, m) {
int a, b, w;
cin >> a >> b >> w;
getmin(d[a][b][1], w);
}
f(l, 2, m) f(k, 1, n) f(i, 1, n) f(j, 1, n) {
int &t = d[i][j][l];
int val = d[i][k][1] + d[k][j][l - 1];
getmin(t, val);
}
cin >> q;
cout << fixed << setprecision(3);
while (q--) {
int x, y;
cin >> x >> y;
ans = INF;
f(l, 1, n - 1) {
if (d[x][y][l] == INF) continue;
ans = min(ans, d[x][y][l] * 1.0 / l);
}
if (ans == INF) cout << "OMG!\n";
else cout << ans << '\n';
}
return 0;
}
D. [SCOI2006]动态最值(线段树 + 树状数组 / 魔改线段树)
题意
有一个包含 \(n\) 个元素的数组,要求实现以下操作:
-
DELETE k:删除位置 \(k\) 上的数。右边的数往左移一个位置(即动态的数组下标)。 -
QUERY i j:查询位置 \(i\sim j\) 上所有数的最小值和最大值。
对于 \(100\%\) 的数据,\(1 \le n, m \le {10}^6\),数组中的元素绝对值均不超过 \({10}^9\)。
思路及代码
线段树 + 树状数组
(考试做法)
设删去一些数后的数组下标为 \(val\)。
每删去一个 \(val_i\) 位置上的数,就在树状数组中对应的 \(i\) 位置上加一,这样查询某个 \(i\) 在树状数组中的前缀和 \(sum(i)\) 就能知道它前面删除了几个数,于是也就能获取到对应的 \(val_i=i-sum(i)\)。
但是,题目中给出的是 \(val_i\),那么怎么求出对应的 \(i\) 呢?我们可以对 \(i\) 进行二分,找出第一个满足 \(i-sum(i)=val_i\) 的就是答案。
时间复杂度 \(O(n\times\log n\times\log n)\),洛谷得分 100pts,码创得分 80pts。
代码:
#include <cstdio>
#include <iostream>
#define f(x, y, z) for (int x = (y); x <= (z); ++x)
#define FILENAME "minmax"
using namespace std;
typedef pair<int, int> pii;
int const N = 1e6 + 10;
int const INF = 0x3f3f3f3f;
int n, m, a[N];
struct BIT {
#define lowbit(x) (x & (-x))
... //省略
} del;
struct SegTree {
#define lson (u << 1)
#define rson (u << 1 | 1)
struct Node {
int l, r, minn, maxx;
} tr[N << 2];
inline void pushup(int u) {
tr[u].minn = min(tr[lson].minn, tr[rson].minn);
tr[u].maxx = max(tr[lson].maxx, tr[rson].maxx);
return;
}
void build(int u, int l, int r) {
tr[u].l = l, tr[u].r = r;
if (l == r) {
tr[u].minn = tr[u].maxx = a[l];
return;
}
int mid = (l + r) >> 1;
build(lson, l, mid);
build(rson, mid + 1, r);
pushup(u);
return;
}
void change(int u, int x, int mn, int mx) {
if (tr[u].l == tr[u].r && tr[u].l == x) {
tr[u].minn = mn;
tr[u].maxx = mx;
return;
}
int mid = (tr[u].l + tr[u].r) >> 1;
if (x <= mid) change(lson, x, mn, mx);
else change(rson, x, mn, mx);
pushup(u);
return;
}
inline void cmp(pii &p, pii q) {
p.first = min(p.first, q.first);
p.second = max(p.second, q.second);
return;
}
pii get_minmax(int u, int l, int r) {
pii res = { INF, -INF };
if (l <= tr[u].l && tr[u].r <= r)
return make_pair(tr[u].minn, tr[u].maxx);
int mid = (tr[u].l + tr[u].r) >> 1;
if (l <= mid) cmp(res, get_minmax(lson, l, r));
if (r > mid) cmp(res, get_minmax(rson, l, r));
return res;
}
} tr;
int val(int x) {
int l = 0, r = n, mid; //注意l的初值为0.因为r可能等于1
while (l + 1 < r) {
mid = (l + r) >> 1;
if (mid - del.sum(mid) < x) l = mid;
else r = mid;
}
return r;
}
signed main() {
ios::sync_with_stdio(false);
cin.tie(0), cout.tie(0);
// freopen(FILENAME ".in", "r", stdin);
// freopen(FILENAME ".out", "w", stdout);
cin >> n >> m;
f(i, 1, n) cin >> a[i];
tr.build(1, 1, n);
f(i, 1, m) {
int op, x, y;
cin >> op;
if (op == 1) {
cin >> x;
x = val(x);
tr.change(1, x, INF, -INF);
del.add(x, 1);
} else if (op == 2) {
cin >> x >> y;
x = val(x), y = val(y);
pii ans = tr.get_minmax(1, x, y);
cout << ans.first << ' ' << ans.second << '\n';
}
}
return 0;
}
魔改线段树
考虑在线段树上直接记录当前区间被删除的情况。记录 \(sum\) 表示当前区间还剩几个数没被删除。
于是我们在查询或删除的时候,直接传入 当前区间第几个没被删除的数。
注意下面的 \(x,l,r\) 都表示当前区间第几个没被删除的数,而不是数组下标。
删除 \(x\):如果当前区间的 \(sum_{lson}\ge x\),说明在左儿子,否则在右儿子。
查询区间 \([l,r]\):设当前线段树区间为 \(u\),讨论三种情况:
- \([l,r]\subseteq[1,sum_{lson}]\),说明在左儿子,查询左儿子中的 \([l,r]\);
- \([l,r]\subseteq[sum_{lson}+1,sum_{u}]\),说明在右儿子,查询右儿子中的 \([l-sum_{lson},r-sum_{lson}]\);
- 否则,说明横跨左儿子和右儿子,分别查询左儿子中的 \([l,sum_{lson}]\) 和右儿子中的 \([1,r-sum_{lson}]\)。
时间复杂度 \(O(n\log n)\)。
代码:
#include <cctype>
#include <cstdio>
#include <iostream>
#define f(x, y, z) for (int x = (y); x <= (z); ++x)
#define FILENAME "minmax"
using namespace std;
typedef pair<int, int> pii;
int const N = 1e6 + 10;
int const INF = 0x3f3f3f3f;
int n, m, a[N];
struct SegTree {
#define lson (u << 1)
#define rson (u << 1 | 1)
struct Node {
int l, r, minn, maxx, sum;
} tr[N << 2];
inline void pushup(int u) {
tr[u].minn = min(tr[lson].minn, tr[rson].minn);
tr[u].maxx = max(tr[lson].maxx, tr[rson].maxx);
tr[u].sum = tr[lson].sum + tr[rson].sum;
return;
}
void build(int u, int l, int r) {
tr[u].l = l ,tr[u].r = r;
if (l == r) {
tr[u].minn = tr[u].maxx = a[l];
tr[u].sum = 1;
return;
}
int mid = (l + r) >> 1;
build(lson, l, mid);
build(rson, mid + 1, r);
pushup(u);
return;
}
void remove(int u, int x) {
if (tr[u].l == tr[u].r) {
tr[u].minn = INF, tr[u].maxx = -INF;
tr[u].sum = 0;
return;
}
int lsum = tr[lson].sum;
if (x <= lsum) remove(lson, x);
else remove(rson, x - lsum);
pushup(u);
return;
}
inline void cmp(pii &p, pii q) {
p.first = min(p.first, q.first);
p.second = max(p.second, q.second);
return;
}
pii get_minmax(int u, int l, int r) {
pii res = {INF, -INF};
if (l == 1 && r == tr[u].sum)
return make_pair(tr[u].minn, tr[u].maxx);
int lsum = tr[lson].sum, rsum = tr[rson].sum;
if (l <= lsum && r > lsum) cmp(res, get_minmax(lson, l, lsum)), cmp(res, get_minmax(rson, 1, r - lsum));
else if (l <= lsum && r <= lsum) cmp(res, get_minmax(lson, l, r));
else if (l > lsum && r <= lsum + rsum) cmp(res, get_minmax(rson, l - lsum, r - lsum));
return res;
}
} tr;
signed main() {
read(n, m); //快读快写模板省略
f(i, 1, n) read(a[i]);
tr.build(1, 1, n);
f(i, 1, m) {
int op, x, y;
read(op);
if (op == 1) {
read(x);
tr.remove(1, x);
} else if (op == 2) {
read(x, y);
pii t = tr.get_minmax(1, x, y);
print(t.first, t.second);
}
}
return 0;
}