20. 有效的括号
题目链接: 20. 有效的括号 - 力扣(LeetCode)题目
给定一个只包括 '(',')','{','}','[',']' 的字符串 s ,判断字符串是否有效。
有效字符串需满足:
左括号必须用相同类型的右括号闭合。
左括号必须以正确的顺序闭合。
每个右括号都有一个对应的相同类型的左括号。
示例 1:
输入:s = "()" 输出:true
示例 2:
输入:s = "()[]{}"
输出:true
示例 3:
输入:s = "(]" 输出:false
思路
先来分析一下 这里有三种不匹配的情况,
-
第一种情况,字符串里左方向的括号多余了 ,所以不匹配。
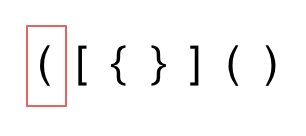
- 第二种情况,括号没有多余,但是 括号的类型没有匹配上。
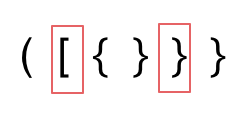
-
第三种情况,字符串里右方向的括号多余了,所以不匹配。
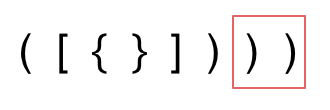
我们的代码需要解决这三种情况:
第一种情况:已经遍历完了字符串,但是栈不为空,说明有相应的左括号没有右括号来匹配,所以return false
第二种情况:遍历字符串匹配的过程中,发现栈里没有要匹配的字符。所以return false
第三种情况:遍历字符串匹配的过程中,栈已经为空了,没有匹配的字符了,说明右括号没有找到对应的左括号return false
那么什么时候说明左括号和右括号全都匹配了呢,就是字符串遍历完之后,栈是空的,就说明全都匹配了。
另外,当遍历到左括号时,我们让响应的右括号入栈,这样就只需要比较当前元素和栈顶相不相等就可以了,比左括号先入栈代码实现要简单的多了!
代码
1 class Solution {
2 public boolean isValid(String s) {
3 Deque<Character> deque = new LinkedList<>();
4 char ch;
5 for (int i = 0; i < s.length(); i++) {
6 ch = s.charAt(i);
7 //碰到左括号,就把相应的右括号入栈
8 if (ch == '(') {
9 deque.push(')');
10 }else if (ch == '{') {
11 deque.push('}');
12 }else if (ch == '[') {
13 deque.push(']');
14 } else if (deque.isEmpty() || deque.peek() != ch) {
15 return false;
16 }else {//如果是右括号判断是否和栈顶元素匹配
17 deque.pop();
18 }
19 }
20 //最后判断栈中元素是否匹配
21 return deque.isEmpty();
22 }
23 }
扩展
括号匹配是使用栈解决的经典问题。
题意其实就像我们在写代码的过程中,要求括号的顺序是一样的,有左括号,相应的位置必须要有右括号。
如果还记得编译原理的话,编译器在 词法分析的过程中处理括号、花括号等这个符号的逻辑,也是使用了栈这种数据结构。
再举个例子,linux系统中,cd这个进入目录的命令我们应该再熟悉不过了。
cd a/b/c/../../
这个命令最后进入a目录,系统是如何知道进入了a目录呢 ,这就是栈的应用(其实可以出一道相应的面试题了)
所以栈在计算机领域中应用是非常广泛的。
有的同学经常会想学的这些数据结构有什么用,也开发不了什么软件,大多数同学说的软件应该都是可视化的软件例如APP、网站之类的,那都是非常上层的应用了,底层很多功能的实现都是基础的数据结构和算法。
所以数据结构与算法的应用往往隐藏在我们看不到的地方!
1047. 删除字符串中的所有相邻重复项
题目链接:1047. 删除字符串中的所有相邻重复项 - 力扣(LeetCode)题目
给出由小写字母组成的字符串 S,重复项删除操作会选择两个相邻且相同的字母,并删除它们。
在 S 上反复执行重复项删除操作,直到无法继续删除。
在完成所有重复项删除操作后返回最终的字符串。答案保证唯一。
示例:
输入:"abbaca" 输出:"ca" 解释: 例如,在 "abbaca" 中,我们可以删除 "bb" 由于两字母相邻且相同,这是此时唯一可以执行删除操作的重复项。
之后我们得到字符串 "aaca",其中又只有 "aa" 可以执行重复项删除操作,所以最后的字符串为 "ca"。
思路
我们在删除相邻重复项的时候,其实就是要知道当前遍历的这个元素,我们在前一位是不是遍历过一样数值的元素,那么如何记录前面遍历过的元素呢?
所以就是用栈来存放,那么栈的目的,就是存放遍历过的元素,当遍历当前的这个元素的时候,去栈里看一下我们是不是遍历过相同数值的相邻元素。
代码
使用 Deque 作为堆栈(Java的api文档中推荐使用Deque)
1 class Solution {
2 public String removeDuplicates(String S) {
3 //ArrayDeque会比LinkedList在除了删除元素这一点外会快一点
4 //参考:https://stackoverflow.com/questions/6163166/why-is-arraydeque-better-than-linkedlist
5 ArrayDeque<Character> deque = new ArrayDeque<>();
6 char ch;
7 for (int i = 0; i < S.length(); i++) {
8 ch = S.charAt(i);
9 if (deque.isEmpty() || deque.peek() != ch) {
10 deque.push(ch);
11 } else {
12 deque.pop();
13 }
14 }
15 String str = "";
16 //剩余的元素即为不重复的元素
17 while (!deque.isEmpty()) {
18 str = deque.pop() + str;
19 }
20 return str;
21 }
22 }
拿字符串直接作为栈,省去了栈还要转为字符串的操作。
class Solution {
public String removeDuplicates(String s) {
// 将 res 当做栈
// 也可以用 StringBuilder 来修改字符串,速度更快
// StringBuilder res = new StringBuilder();
StringBuffer res = new StringBuffer();
// top为 res 的长度
int top = -1;
for (int i = 0; i < s.length(); i++) {
char c = s.charAt(i);
// 当 top > 0,即栈中有字符时,当前字符如果和栈中字符相等,弹出栈顶字符,同时 top--
if (top >= 0 && res.charAt(top) == c) {
res.deleteCharAt(top);
top--;
// 否则,将该字符 入栈,同时top++
} else {
res.append(c);
top++;
}
}
return res.toString();
}
}
拓展:双指针
class Solution {
public String removeDuplicates(String s) {
char[] ch = s.toCharArray();
int fast = 0;
int slow = 0;
while(fast < s.length()){
// 直接用fast指针覆盖slow指针的值
ch[slow] = ch[fast];
// 遇到前后相同值的,就跳过,即slow指针后退一步,下次循环就可以直接被覆盖掉了
if(slow > 0 && ch[slow] == ch[slow - 1]){
slow--;
}else{
slow++;
}
fast++;
}
return new String(ch,0,slow);
}
}
扩展
这道题目就像是我们玩过的游戏对对碰,如果相同的元素挨在一起就要消除。
可能我们在玩游戏的时候感觉理所当然应该消除,但程序又怎么知道该如何消除呢,特别是消除之后又有新的元素可能挨在一起。
此时游戏的后端逻辑就可以用一个栈来实现(我没有实际考察对对碰或者爱消除游戏的代码实现,仅从原理上进行推断)。
游戏开发可能使用栈结构,编程语言的一些功能实现也会使用栈结构,实现函数递归调用就需要栈,但不是每种编程语言都支持递归,例如:
递归的实现就是:每一次递归调用都会把函数的局部变量、参数值和返回地址等压入调用栈中,然后递归返回的时候,从栈顶弹出上一次递归的各项参数,所以这就是递归为什么可以返回上一层位置的原因。
相信大家应该遇到过一种错误就是栈溢出,系统输出的异常是 Segmentation fault(当然不是所有的Segmentation fault 都是栈溢出导致的) ,如果你使用了递归,就要想一想是不是无限递归了,那么系统调用栈就会溢出。
而且在企业项目开发中,尽量不要使用递归!在项目比较大的时候,由于参数多,全局变量等等,使用递归很容易判断不充分return的条件,非常容易无限递归(或者递归层级过深),造成栈溢出错误(这种问题还不好排查!)
150. 逆波兰表达式求值
题目链接:150. 逆波兰表达式求值 - 力扣(LeetCode)题目
给你一个字符串数组 tokens ,表示一个根据 逆波兰表示法 表示的算术表达式。
请你计算该表达式。返回一个表示表达式值的整数。
注意:
- 有效的算符为 '+'、'-'、'*' 和 '/' 。
- 每个操作数(运算对象)都可以是一个整数或者另一个表达式。
- 两个整数之间的除法总是 向零截断 。
- 表达式中不含除零运算。
- 输入是一个根据逆波兰表示法表示的算术表达式。
- 答案及所有中间计算结果可以用 32 位 整数表示。
示例 1:
输入:tokens = ["2","1","+","3","*"] 输出:9
解释:该算式转化为常见的中缀算术表达式为:((2 + 1) * 3) = 9
示例 2:
输入:tokens = ["4","13","5","/","+"] 输出:6 解释:该算式转化为常见的中缀算术表达式为:(4 + (13 / 5)) = 6
示例 3:
输入:tokens = ["10","6","9","3","+","-11","*","/","*","17","+","5","+"] 输出:22 解释:该算式转化为常见的中缀算术表达式为: ((10 * (6 / ((9 + 3) * -11))) + 17) + 5 = ((10 * (6 / (12 * -11))) + 17) + 5 = ((10 * (6 / -132)) + 17) + 5 = ((10 * 0) + 17) + 5 = (0 + 17) + 5 = 17 + 5 = 22
逆波兰表达式:
逆波兰表达式是一种后缀表达式,所谓后缀就是指算符写在后面。
- 平常使用的算式则是一种中缀表达式,如 ( 1 + 2 ) * ( 3 + 4 ) 。
- 该算式的逆波兰表达式写法为 ( ( 1 2 + ) ( 3 4 + ) * ) 。
逆波兰表达式主要有以下两个优点:
- 去掉括号后表达式无歧义,上式即便写成 1 2 + 3 4 + * 也可以依据次序计算出正确结果。
- 适合用栈操作运算:遇到数字则入栈;遇到算符则取出栈顶两个数字进行计算,并将结果压入栈中
思路
本题有点像上题中的对对碰,只不过把相邻元素做消除了变为做运算!
代码
1 class Solution {
2 public int evalRPN(String[] tokens) {
3 Deque<Integer> stack = new LinkedList();
4 for (String s : tokens) {
5 if ("+".equals(s)) { // leetcode 内置jdk的问题,不能使用==判断字符串是否相等
6 stack.push(stack.pop() + stack.pop()); // 注意 - 和/ 需要特殊处理
7 } else if ("-".equals(s)) {
8 stack.push(-stack.pop() + stack.pop());
9 } else if ("*".equals(s)) {
10 stack.push(stack.pop() * stack.pop());
11 } else if ("/".equals(s)) {
12 int temp1 = stack.pop();
13 int temp2 = stack.pop();
14 stack.push(temp2 / temp1);
15 } else {
16 stack.push(Integer.valueOf(s));
17 }
18 }
19 return stack.pop();
20 }
21 }
扩展
其实逆波兰表达式相当于是二叉树中的后序遍历。 大家可以把运算符作为中间节点,按照后序遍历的规则画出一个二叉树。
我们习惯看到的表达式都是中缀表达式,因为符合我们的习惯,但是中缀表达式对于计算机来说就不是很友好了。
例如:4 + 13 / 5,这就是中缀表达式,计算机从左到右去扫描的话,扫到13,还要判断13后面是什么运算符,还要比较一下优先级,然后13还和后面的5做运算,做完运算之后,还要向前回退到 4 的位置,继续做加法,你说麻不麻烦!
那么将中缀表达式,转化为后缀表达式之后:["4", "13", "5", "/", "+"] ,就不一样了,计算机可以利用栈来顺序处理,不需要考虑优先级了。也不用回退了, 所以后缀表达式对计算机来说是非常友好的。
可以说本题不仅仅是一道好题,也展现出计算机的思考方式。
标签:deque,ch,随想录,括号,字符串,求值,stack,表达式 From: https://www.cnblogs.com/xpp3/p/17113789.html