Kinodynamc planning 满足动力学约束的路径规划
State Lattice Planning
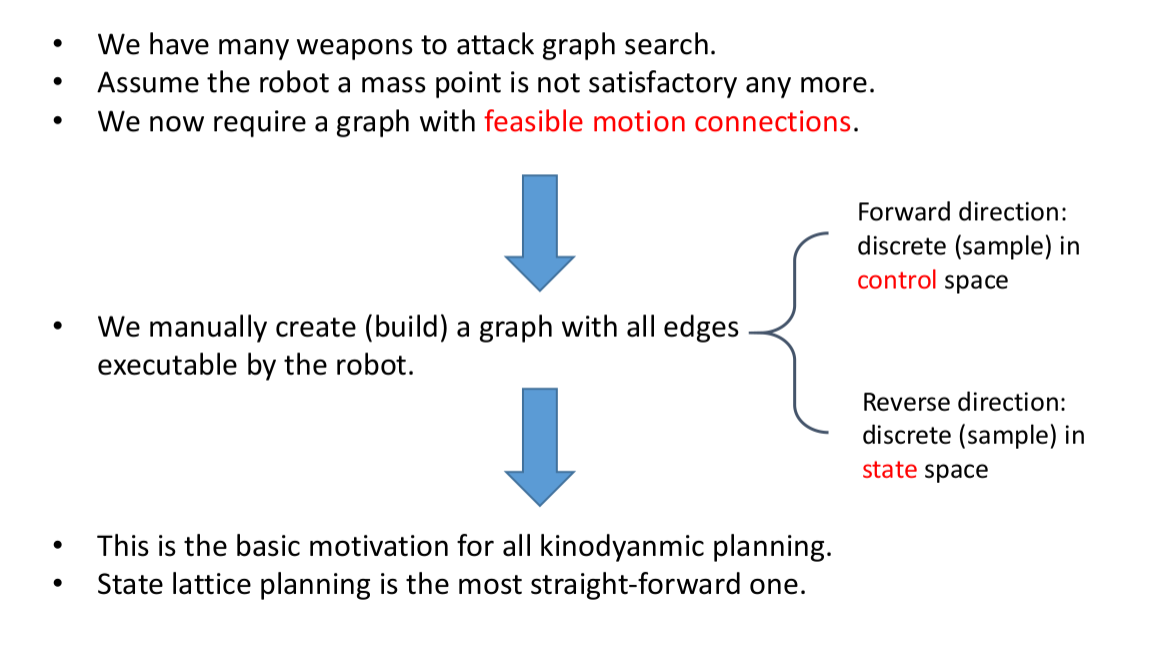
之前两节课的运动规划都是不考虑运动约束将机器人看成一个质点,而实际问题则是需要考虑运动学约束的
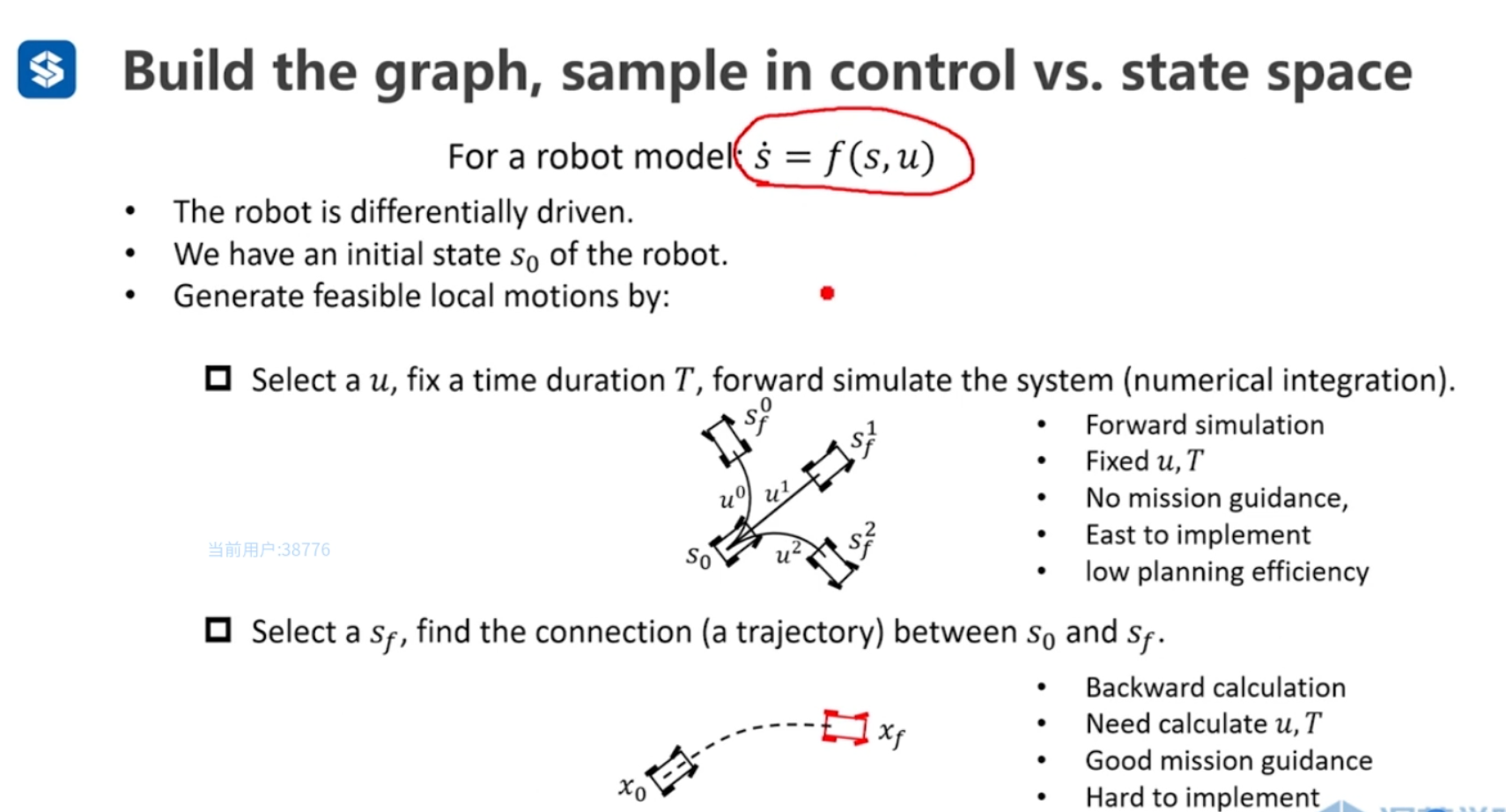
- 建立运动学方程 \({{\dot{s} = f(s,u)}}\)
- 已知初始状态 \(s_{0}\)
- 通过两种方式生成局部可行的运动
- 前向模拟:在控制空间采样,通过采样控制量,推算下一步车的位置。优点是容易实现,缺点是非任务导向的、效率低
- 反向计算:在状态空间采样,通过采样空间中的位置,反算两点之间的控制量,反算边,优点是任务导向,缺点是难实现
前向模拟
- 建立系统的状态空间方程
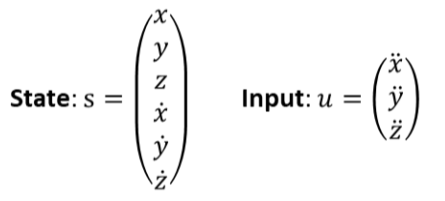
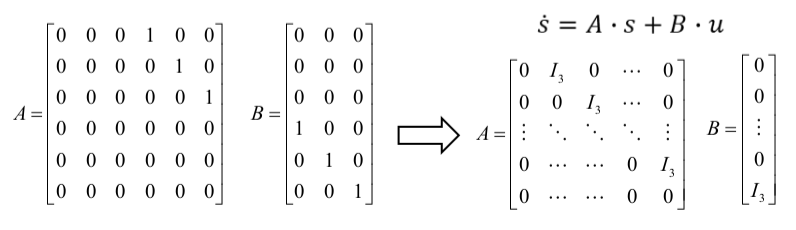
- 已知初始状态,离散加速度,对于不同的输入,固定T,积分出不同的最终状态
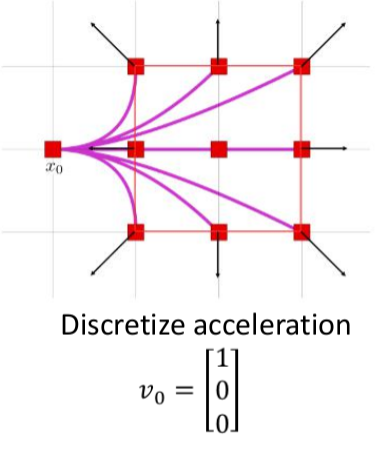
- 已知初始状态,离散jerk,对于不同的输入,固定T,积分出不同的最终状态
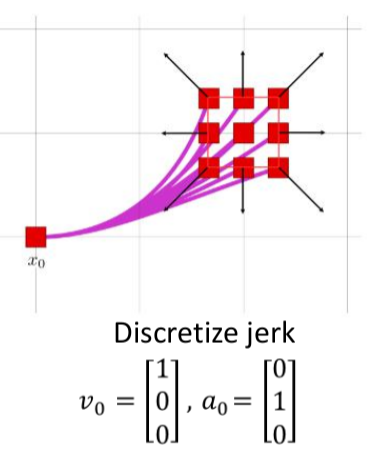
- 利用状态转移方程,可以推导出每一时刻的状态,进而求解出轨迹
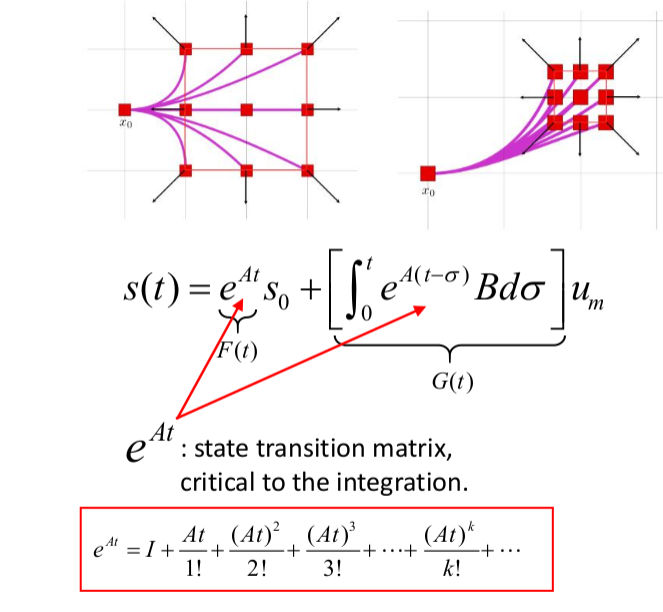
注:如果A是幂零矩阵,计算 $e^{At}$ 展开就会比较简单
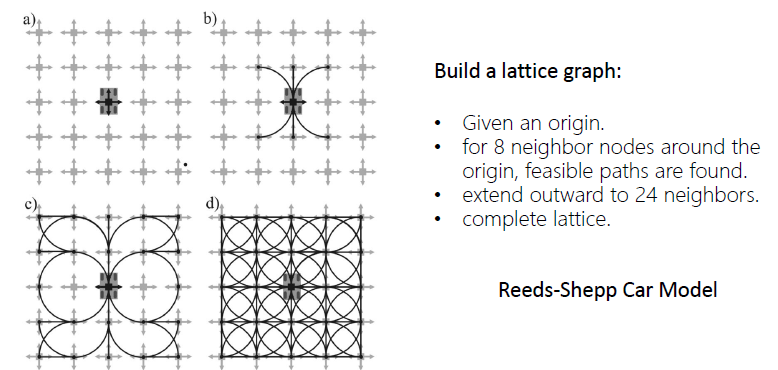
构建lattice graph
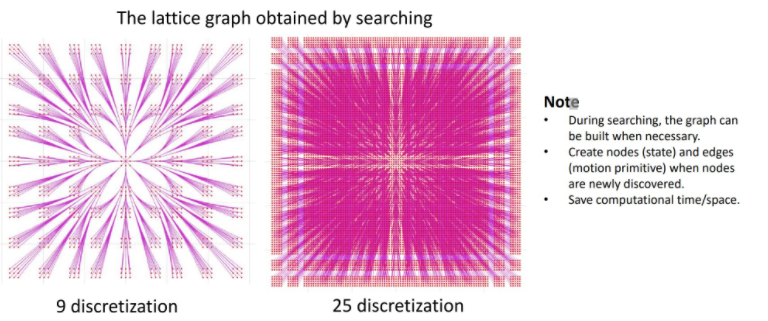
可以再搜索的过程中,在需要的时候进行构建lattice graph,这样可以节省时间和空间
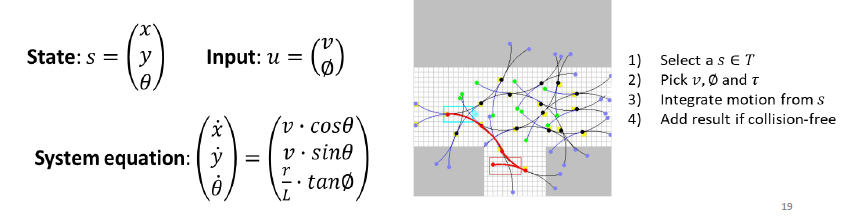
反向计算
对状态空间进行采样
对比
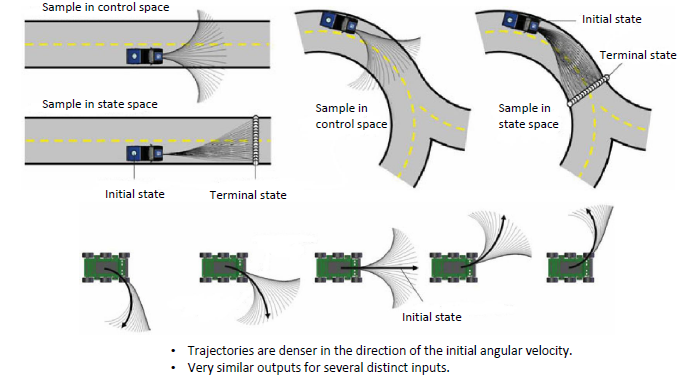
相较于在状态空间采样,在控制空间采样得到的轨迹更没有目的性,而且会由于初始状态的原因,导致各个轨迹之间产生同质的现象,导致一条路径fail其他路径也很容易fail,但是在状态空间采样反算轨迹是非常困难的,这样就涉及了Boundary Value Problem。
OBVP
问题背景
例如一个5次多项式表示两点间的轨迹方程
\[x(t)=c_{5}t^{5}+c_{4}t^{4}+c_3t^{3}+c_{2}t^{2}+c_{1}t+c_{0} \]已知在\(t=0\)和\(t=T\)时刻,位置、速度、加速度如下
| p | v | a | |
|---|---|---|---|
| t = 0 | a | 0 | 0 |
| t = T | b | 0 | 0 |
那么解下面这个方程组就称为BVP问题,解BVP本身并不难,难在如何求最优解,即OBVP问题
\[\left[\begin{array}{l}\mathrm{a} \\\mathrm{b} \\0 \\0 \\0 \\0 \\0\end{array}\right]=\left[\begin{array}{c}\mathrm{x}(0) \\\mathrm{x}(\mathrm{T}) \\\mathrm{x}^{\prime}(0) \\\mathrm{x}^{\prime}(\mathrm{T}) \\\mathrm{x}^{\prime \prime}(0) \\\mathrm{x}^{\prime \prime}(\mathrm{T})\end{array}\right]=\left[\begin{array}{c}\mathrm{x}(0) \\\mathrm{x}(\mathrm{T}) \\\mathrm{v}(0) \\\mathrm{v}(\mathrm{T}) \\\mathrm{a}(0) \\\mathrm{a}(\mathrm{T})\end{array}\right]=\left[\begin{array}{cccccc}0 & 0 & 0 & 0 & 0 & 1 \\\mathrm{~T}^{5} & \mathrm{~T}^{4} & \mathrm{~T}^{3} & \mathrm{~T}^{2} & \mathrm{~T} & 1 \\0 & 0 & 0 & 0 & 1 & 0 \\5 \mathrm{~T}^{4} & 4 \mathrm{~T}^{3} & 3 \mathrm{~T}^{2} & 2 \mathrm{~T} & 1 & 0 \\0 & 0 & 0 & 2 & 0 & 0 \\20 \mathrm{~T}^{3} & 12 \mathrm{~T}^{2} & 6 \mathrm{~T} & 2 & 0 & 0\end{array}\right]\left[\begin{array}{c}\mathrm{c}_{5} \\\mathrm{c}_{4} \\\mathrm{c}_{3} \\\mathrm{c}_{2} \\\mathrm{c}_{1} \\\mathrm{c}_{0}\end{array}\right] \]原理
- 一般
**cost function**由两部分组成,final state cost:最终状态的惩罚项H
,transition cost:整个系统状态转移的损失G
其中s为状态变量,u为输入变量
- 构建系统的Hamiltonian矩阵H,引入协变量\(\lambda\)
其中\(\lambda = (\lambda_{1},\lambda_{2},\lambda_{3})^{T}\) $$,\(\lambda\)的维数与\(f_{s}(s,u)\)输出维数相同
- 根据Pontrayagin’s 最小值原理得出最优的轨迹
- 通过Hamiltonian矩阵对s求导得到\(\dot{\lambda}\)
其中对s的各个元素求导就是对应的\(\dot{\lambda_{i}}\) ,例如\(s=(p,v,a)\),对p求导得\(\dot{\lambda_{1}}\) ,对v求导得\(\dot{\lambda_{2}}\) ,对a求导得\(\dot{\lambda_{3}}\) 。
- 构造\(\lambda(t)\)的解,代入Hamiltonian矩阵中,并且最小化输入变量\(u(t)\),得出最优的输入变量\(u^{*}(t)\)
- 通过将最优输入变量\(u^{*}(t)\)进行积分,得到最优轨迹\(s^{*}(t)\)
- 通过最优变量以及结合边界条件,得出最优轨迹\(s^{*}(t)\)中的参数
Example
以三轴无人机系统为例,求解OBVP问题的过程如下:
- 建模
将无人机的三个维度进行解耦,单独优化每一维
- 最优化目标函数:\(J=\frac{1}{T}\int_{0}^{T} j^{2}(t)dt\)
这里的 cost function 不包含 final state cost,因为要求最后一定要准确到达指定状态,以\(\frac{1}{T} j^{2}\) 作为 transition cost 即\(g(s,u) = \frac{1}{T} j^{2}\) ,因此有
\[\begin{split}& H=\left\{\begin{array}{ll}0 & \text { if } \quad s=s(T) \\\infty & \text { other }\end{array}\right.\\& G=\int_{0}^{T}g(s,u)dt=\int_{0}^{T}\frac{1}{T} \times j(t)^{2}\end{split} \]- 状态变量:\(s(t) = (p,v,a)\)
- 系统输入:\(u(t) = j\)
- 系统状态方程:\(\dot{s}(t) = f_{s}(s,u)=(v,a,j)\)
- 构建Hamitonian函数
- H 对 s 求导得 \(\dot{\lambda }\)
其中:
\[\begin{split}& \dot{\lambda_{1}} = -\frac{\partial H}{\partial p} = 0 \\ & \dot{\lambda_{2}} = -\frac{\partial H}{\partial v} = -\lambda_{1} \\& \dot{\lambda_{3}} = -\frac{\partial H}{\partial v} = -\lambda_{2}\end{split} \]-
构造出\(\lambda\)一个解,其中\(\alpha,\beta,\gamma\) 均为引入待求解的参数
\[\lambda (t)= \frac{1}{T} \begin{bmatrix}-2\alpha \\ 2\alpha t + 2\beta \\ -\alpha t^{2} -2\beta t - 2\gamma \end{bmatrix} \] -
求出最优输入\(u^{*}(t)\),在s取最优解\(s^{*}\)的条件下,使H最小的u
- 积分\(u^{*}(t)\)求出最优\(s^{*}(t)\),并且满足初始状态\(s(0)=(p_{0},v_{0},a_{0})\)
-
利用最终状态\(s^{*}(T) = s_{f}\),求出\(\alpha\) \(\beta\) \(\gamma\)
\[\begin{split}{\color{Black} {s^{*}(T)=\left[\begin{array}{c}\frac{\alpha}{120} T^{5}+\frac{\beta}{24} T^{4}+\frac{\gamma}{6} T^{3}+\frac{a_{0}}{2} T^{2}+v_{0} T+p_{0} \\\frac{\alpha}{24} T^{4}+\frac{\beta}{6} T^{3}+\frac{\gamma}{2} T^{2}+a_{0} T+v_{0} \\\frac{\alpha}{6} T^{3}+\frac{\beta}{2} T^{2}+\gamma T+a_{0}\end{array}\right]} =s_{f}=\begin{bmatrix}p_{f} \\v_{v}\\a_{f}\end{bmatrix}{\large } {\large } } \end{split} \]
化简得:
\[\left[\begin{array}{ccc}\frac{1}{120} T^{5} & \frac{1}{24} T^{4} & \frac{1}{6} T^{3} \\\frac{1}{24} T^{4} & \frac{1}{6} T^{3} & \frac{1}{2} T^{2} \\\frac{1}{6} T^{3} & \frac{1}{2} T^{2} & T\end{array}\right]\left[\begin{array}{l}\alpha \\\beta \\\gamma\end{array}\right]=\left[\begin{array}{c}\Delta p \\\Delta v \\\Delta a\end{array}\right] \]\[\left[\begin{array}{c}\Delta p \\\Delta v \\\Delta a\end{array}\right]=\left[\begin{array}{c}p_{f}-p_{0}-v_{0} T-\frac{1}{2} a_{0} T^{2} \\v_{f}-v_{0}-a_{0} T \\a_{f}-a_{0}\end{array}\right] \]\[{\color{Red} \left[\begin{array}{c} \alpha \\ \beta \\ \gamma \end{array}\right]=\frac{1}{T^{5}}\left[\begin{array}{ccc} 720 & -360 T & 60 T^{2} \\ -360 T & 168 T^{2} & -24 T^{3} \\ 60 T^{2} & -24 T^{3} & 3 T^{4} \end{array}\right]\left[\begin{array}{c} \Delta p \\ \Delta v \\ \Delta a \end{array}\right]} \]可以看到\(\alpha\) \(\beta\) \(\gamma\)只与初始状态和最终状态有关,因此给定T,就可以算出\(\alpha\) \(\beta\) \(\gamma\)
进而就可以得到 \(s^{*}(t)\) 和 \(j^{*}(t)\)
cost 也可以计算出来
\[{\color{Red} J=\gamma^{2}+\beta \gamma T+\frac{1}{3} \beta^{2} T^{2}+\frac{1}{3} \alpha \gamma T^{2}+\frac{1}{4} \alpha \beta T^{3}+\frac{1}{20} \alpha^{2} T^{4}} \]- 如果没有给定T,J 对 T 求导,求出最优的T
a. 对于 Fixed final state 问题,final state的惩罚项是不可以求导的,那么就可以根据最终状态值进行各参数的确定
\[h(s(T))=\left\{\begin{array}{ll}0, & \text { if } s=s(T) \\\infty, & \text { otherwise }\end{array}\right. \]b. 对于 partially-free final state 问题,最终状态的一部分是指定的,即
\[\text { given } s_{i}(T), i \in I \]那么就需要利用极小值原理的边界条件,对自由分量求导
\[\lambda_{j}(T)=\frac{\partial h\left(s^{*}(T)\right)}{\partial s_{j}}, \text { for } j \neq i \]例如:对于最终位置为固定值\(p_{f}\),但最终的速度和加速度为自由的最终状态,即\(s^{*}(T) = (p_{f},*,*)^{T}\)
\[\begin{split}H(s,u,\lambda) & = g(s,u) + {\lambda}^{T}f_{s}(s,u)\\ &=\frac{1}{T}j^{2} + (\lambda_{1},\lambda_{2},\lambda_{3})^{T}(v,a,j)\\ &= \frac{1}{T}j^{2} + \lambda_{1}v + \lambda_{2}a + \lambda_{3}j \\ \end{split} \]\[\dot{\lambda } = -\nabla H(s^{*},u^{*},\lambda) = (0,-\lambda_{1},-\lambda_{2}) \]\[\lambda (t)= \frac{1}{T} \begin{bmatrix}-2\alpha \\ 2\alpha t + 2\beta \\ -\alpha t^{2} -2\beta t - 2\gamma \end{bmatrix} \]因为末状态v,a自由,因此h的表达式与T时刻的v和并不相关,因此
\[\lambda_{2}(T)=\frac{\partial h\left(s^{*}(T)\right)}{\partial v} = 0 \]\[\lambda_{3}(T)=\frac{\partial h\left(s^{*}(T)\right)}{\partial a} = 0 \]代入\(\lambda(t)\)解得:
\[\left\{\begin{array}{l}\beta=-\alpha T \\\gamma=\frac{\alpha}{2} T^{2}\end{array}\right. \]\[\lambda (t)=\frac{1}{T} \begin{bmatrix}-2\alpha \\2\alpha (t-T) \\-\alpha t^{2}+2\alpha Tt-\alpha T^{2}\end{bmatrix} \]- 与前面相同,求出最优输入\(u^{*}(t)\)(在s取最优解\(s^{*}\)的条件下,使H最小的u)
- 积分\(u^{*}(t)\)求出最优\(s^{*}(t)\),并且满足初始状态\(s(0)=(p_{0},v_{0},a_{0})\)
- 根据末状态已知量,即\(s^{*}(T) = (p_{f},*,*)^{T}\) ,求出\(\alpha\)
- 代入 \(\alpha\) 解出\(u^{*}(t)\)和\(s^{*}(t)\),再对\(u^{*}(t)\)积分求出J
- 可以看到J只与T有关,令\(\frac{dJ}{dT} = 0\) 解出最优积分时间 \(T^{*}\)
实际使用时,T不能为虚数和负数,比较剩下的T(正数)其cost的大小,令cost最小的\(T\)为\(T^{*}\)
构建完lattice graph后,就是search的问题
设计启发函数
原则:分解成简单的问题
- 不考虑障碍物
- 不考虑动力学
Hybrid A*
A*不考虑运动学约束,而lattice又太过于稠密。那使用栅格来剪枝lattice生成的轨迹,就可以既符合运动学约束,又不至于太过于稠密。
核心思想就是,每个栅格中只能有一个点。
Hybrid A 相较于 A 的区别**

- \(f(n) g(n) h(n)\) 计算不同
- 在从容器中拿出一个结点,要扩展这个结点,不是通过4连接或者8连接,而是通过生成lattice来扩展这个结点
- 扩展结点之后,生成的新的点可能已经落在已经有点的格子里,这就要比较新生成的点的cost和之前的cost,如果新生成的cost少的话,还需要更新这个格子中点的信息。
- 在容器中找到一个结点时,要利用启发函数,这个启发函数不仅仅是欧式距离这么简单,要考虑non-holonomic和obstacles的约束
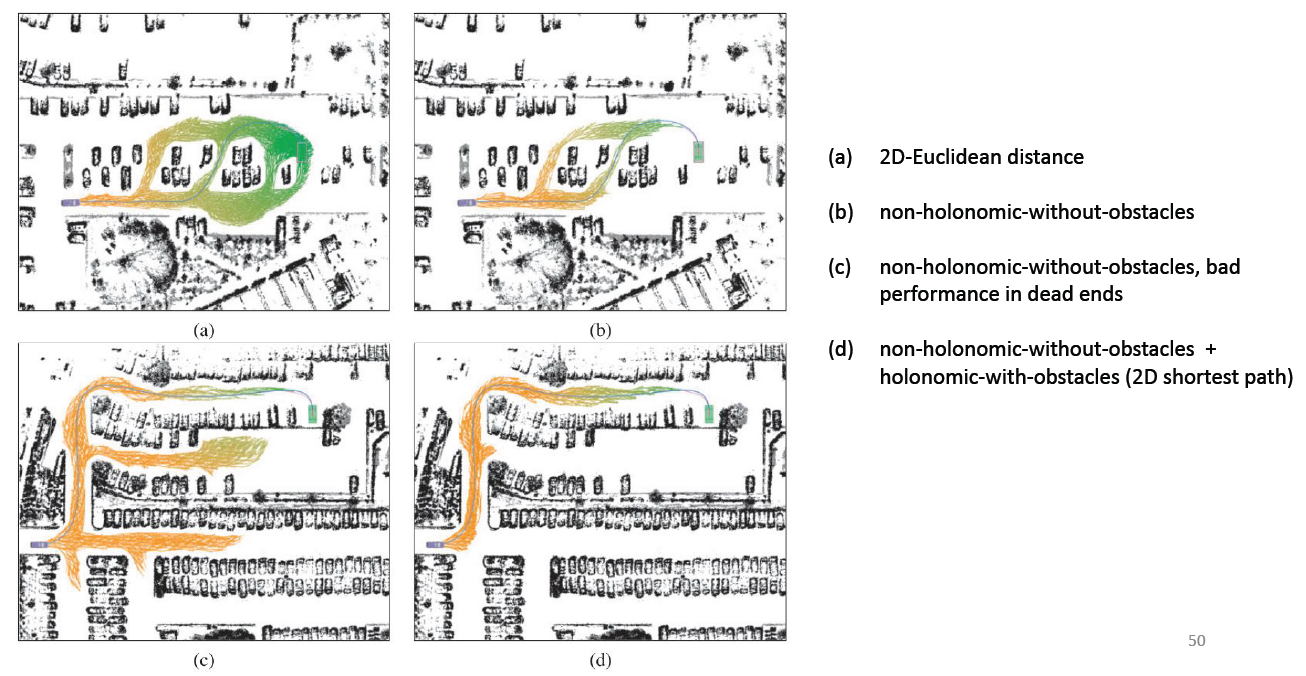
Analytic Expansions:以一定概率,在某次扩展树之后,直接尝试生成一条由当前节点联通目标位置的轨迹,如果该轨迹不碰撞障碍物,就可以结束了。
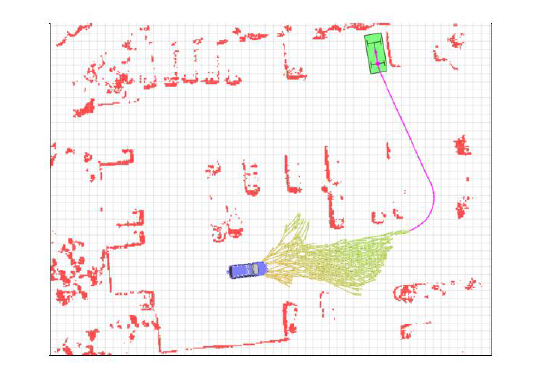
Kinodynamc RRT*
与RRT*的区别
- 连接两点时不是直接连接而是解一个两点边界值BVP问题(最好是OBVP问题)
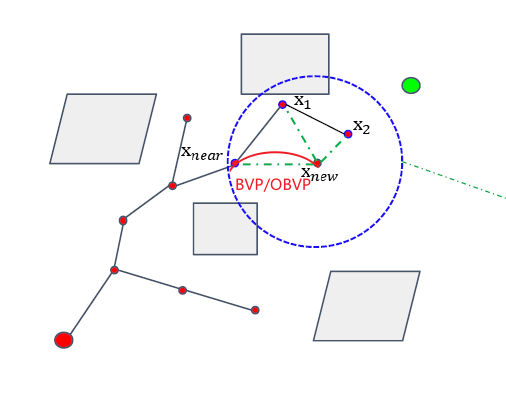
- 采样新的点不是在坐标空间中,而是在状态空间中。例如,如果状态空间包括(p,v),位置和速度,那么就是6维空间\((x,y,z,\dot{x},\dot{y},\dot{z})^{T}\)

- 将新采样的节点与树上的节点连接时,使用最优控制的方法解(O)BVP问题
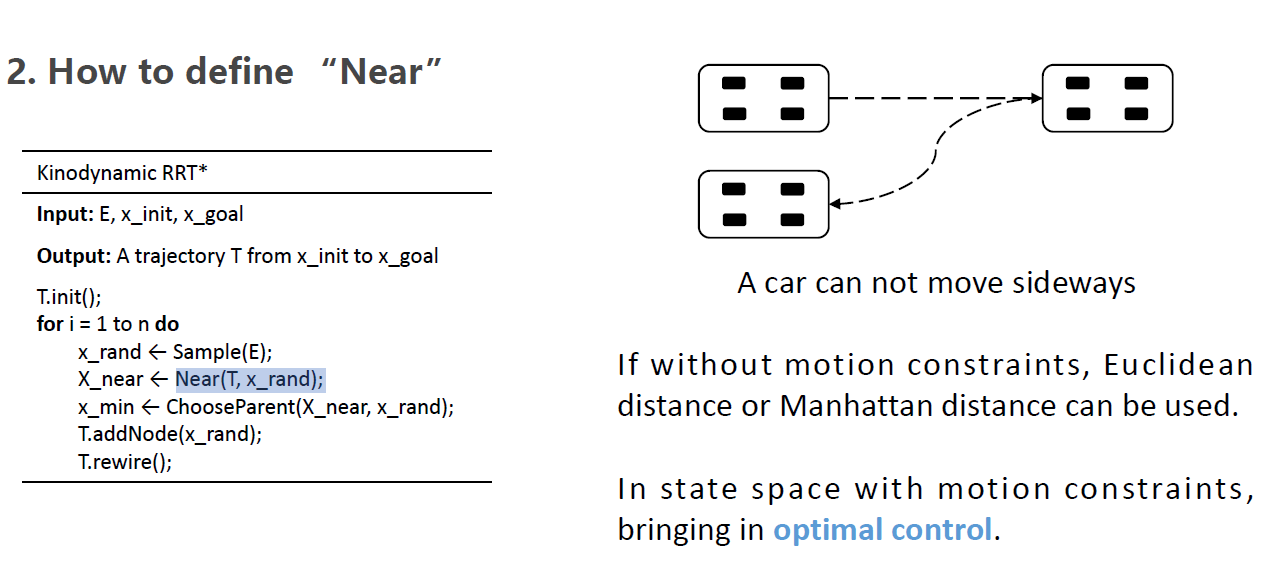
- 计算 x_{new}的邻域不是使用欧式距离,而是一定的cost之内。在RRT中,在采样到一个 \(x_{new}\)
,要找个一个邻域内所有点。在Kinodynamic RRT*中,这个邻域是用cost计算,计算这个邻域是有标准的方法的。