题解 SP2666【Query on a tree IV】

题目分析

首先，对原树进行轻重链剖分，并对于每一条重链分别建一颗线段树（原因下文会提到）。

令 \(dfn\) 为某个点的 dfs 序，\(rnk(i)\) 为 \(dfn\) 为 \(i\) 的点的编号。

我们规定对于一条重链上的一条子链，其左端点为这条子链上 \(dfn\) 最小的点，右端点为这条子链上 \(dfn\) 最大的点。

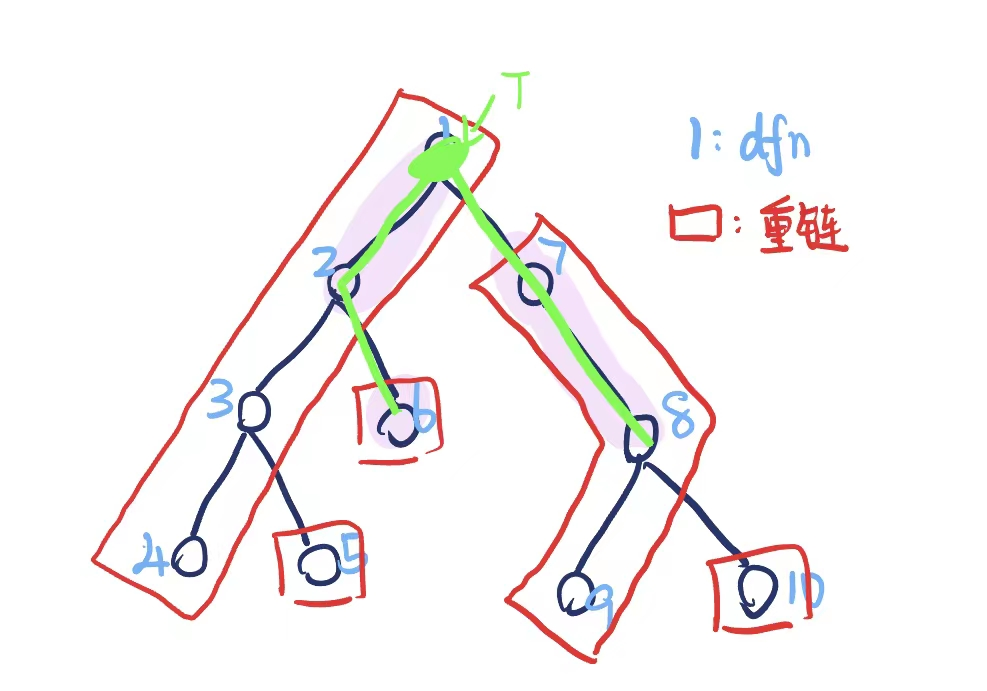
对于树上的一条路径，我们假设它的最高点为 \(tp\)，可将这条路径分为三段：

1. \(tp\) 所在重链上一段。
2. 重链上那一段的左端点向下延伸到这条路径的某个端点一段（不含左端点）。
3. 重链上那一段的右端点向下延伸到这条路径的另一个端点一段（不含右端点）。

比如下图中的绿色路径，分成了紫色的三段。

对于线段树的每个节点，假设其维护的链上的点的 \(dfn\) 属于 \([l,r]\)。

我们定义一条路径为特殊路径当且仅当它的 \(tp\) 和特殊端点属于同一条重链，非特殊端点为白点（或者不存在）且这条路径的第 1 段上的所有点的 \(dfn\) 都属于 \([l,r]\)。（非特殊端点为路径有两个端点时除去特殊端点的另一个端点）

特别地，若没有规定特殊端点，特殊路径则只需满足第 1 段上的所有点的 \(dfn\) 都属于 \([l,r]\)。

对于线段树的每个节点，维护以下三个值：

• \(lmx\)：表示将点 \(rnk(l)\) 作为特殊端点的特殊路径的最大长度。
• \(rmx\)：表示将点 \(rnk(r)\) 作为特殊端点的特殊路径的最大长度。
• \(mx\): 表示两个端点均为白点的特殊路径的最大长度。

如何建树呢？

我们定义 \(dep(x)\) 为点 \(x\) 到根节点的距离，\(dis(x,y)\) 为点 \(x\) 到点 \(y\) 的距离，\(mx1(x)\) 为点 \(x\) 向下第一步不走重边能到的最远的白点的距离，\(mx2(x)\) 为点 \(x\) 向下第一步不走重边能到的次远的白点的距离。

当 \(x\) 和 \(y\) 属于同一条重链时，显然有 \(dis(x,y)=|dep(x) - dep(y)|\)。

我们对于每个点 \(x\) 都用一个大根堆维护 \(x\) 向下第一步不走重边能到的所有白点的极大距离，利用 \(x\) 每个轻儿子所在重链的线段树的 \(lmx\) 即可求出（因为轻儿子一定为它所在重链的左端点）。

观察到，我们在 build 某条重链的线段树时，需要这条重链上每个点的轻儿子所在重链的线段树完全建好，因此需要对每一条重链分别建树。

对于线段树 \(l=r\) 的节点，设 \(x=rnk(l)\)：

若 \(x\) 为白点，则 \(lmx=rmx=\max(0, mx1(x)),mx=\max(0,mx1(x),mx1(x)+mx2(x))\)。

若 \(x\) 为黑点，则 \(lmx=rmx=mx1(x),mx=mx1(x)+mx2(x)\)。

类似最大子段和，我们可以容易得出如何 pushup。

void pushup(int p, int l, int r) {
    int ls = t[p].ls, rs = t[p].rs, mid = l + r >> 1;
    t[p].lmx = max(t[ls].lmx, t[rs].lmx + dep[rnk[mid + 1]] - dep[rnk[l]]);
    t[p].rmx = max(t[rs].rmx, t[ls].rmx + dep[rnk[r]] - dep[rnk[mid]]);
    t[p].mx = max(max(t[ls].mx, t[rs].mx), t[ls].rmx + t[rs].lmx + dep[rnk[mid + 1]] - dep[rnk[mid]]);
}

这样，线段树就维护好了。

接下来，我们考虑怎么修改一个点的颜色。
设被修改的点为 \(u\)，则首先要在 \(u\) 所在重链的线段树上进行单点改。

由于 \(u\) 所在重链上的 \(tp\) 一定是它父亲的轻儿子，所以它父亲的线段树节点也会发生变化。

因此，我们需要沿着重链一直向上跳，直到当前重链的 \(tp\) 为根节点为止。

下图为修改 \(rnk(10)\) 的过程。

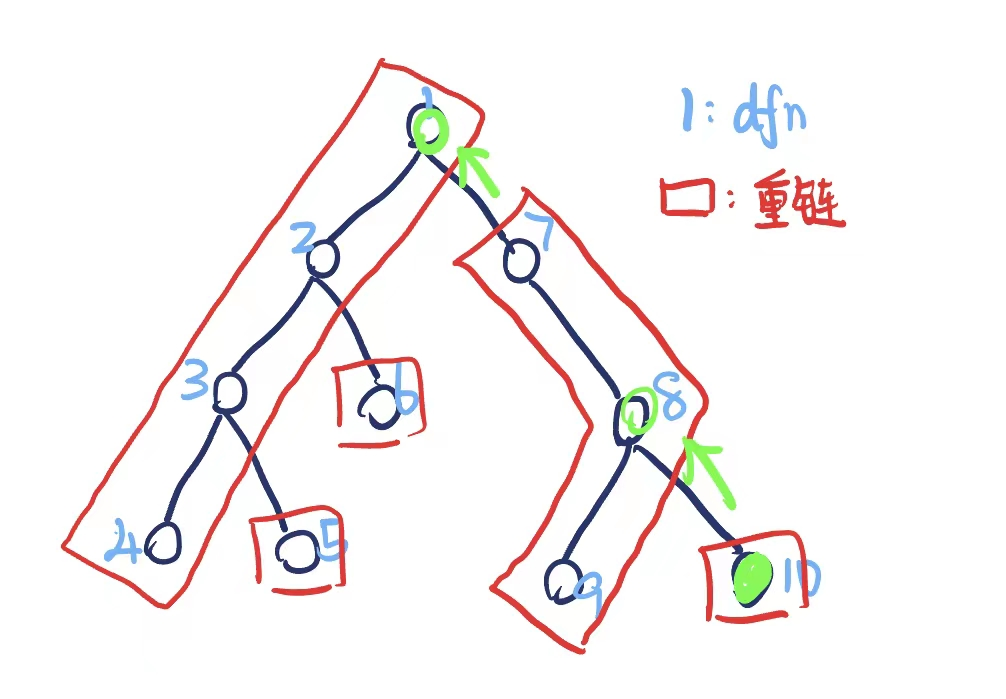
最多跳 \(\log n\) 次，线段树和堆的复杂度均为 \(O(\log n)\)，所以一次修改的复杂度为 \(O(\log^2 n)\)。

我们用一个大根堆 \(ans\) 维护每条重链线段树的 \(mx\)，便可 \(O(1)\) 查询。

因此，总复杂度为 \(O(q \log ^2 n)\)。

完整代码

#include <bits/stdc++.h>
using namespace std;

const int MAXN = 1e5 + 5, INF = 1e9;

int n, col[MAXN];

struct Edge {int to, w;};
vector<Edge> e[MAXN];

int fa[MAXN], sz[MAXN], dep[MAXN], hson[MAXN];

void dfs1(int x, int fth) {
    sz[x] = 1, hson[x] = -1;
    for (auto y : e[x]) {
        if (y.to == fth) continue;
        dep[y.to] = dep[x] + y.w, fa[y.to] = x, dfs1(y.to, x), sz[x] += sz[y.to];
        if (hson[x] < 0 || sz[y.to] > sz[hson[x]]) hson[x] = y.to;
    }
}

int dfn[MAXN], rnk[MAXN], top[MAXN], tim, len[MAXN];

void dfs2(int x, int tp) {
    top[x] = tp, dfn[x] = ++tim, rnk[tim] = x, len[tp]++;
    if (hson[x] < 0) return;
    dfs2(hson[x], tp);
    for (auto y : e[x])
        if (y.to != hson[x] && y.to != fa[x]) dfs2(y.to, y.to);
}

struct Queue {
    priority_queue<int> q1, q2;
    void insert(int v) {if (v != -INF) q1.push(v);}
    void erase(int v) {if (v != -INF) q2.push(v);}
    int top() {
        while (1) {
            if (q1.empty()) return -INF;
            if (q2.empty() || q1.top() != q2.top()) return q1.top();
            q1.pop(), q2.pop();
        }
    }
}hp[MAXN], ans;

struct Segment {int ls, rs, lmx, rmx, mx;} t[MAXN << 2];
int tot, rt[MAXN];

void pushup(int p, int l, int r) {
    int ls = t[p].ls, rs = t[p].rs, mid = l + r >> 1;
    t[p].lmx = max(t[ls].lmx, t[rs].lmx + dep[rnk[mid + 1]] - dep[rnk[l]]);
    t[p].rmx = max(t[rs].rmx, t[ls].rmx + dep[rnk[r]] - dep[rnk[mid]]);
    t[p].mx = max(max(t[ls].mx, t[rs].mx), t[ls].rmx + t[rs].lmx + dep[rnk[mid + 1]] - dep[rnk[mid]]);
}
void build(int &p, int l, int r) {
    if (!p) p = ++tot;
    if (l == r) {
        int x = rnk[l];
        for (auto y : e[x]) {
            if (y.to == fa[x] || y.to == hson[x]) continue;
            hp[x].insert(t[rt[y.to]].lmx + dep[y.to] - dep[x]);
        }
        int mx1 = hp[x].top(); hp[x].erase(mx1);
        int mx2 = hp[x].top(); hp[x].insert(mx1);
        t[p].lmx = t[p].rmx = max(0, mx1), t[p].mx = max(0, max(mx1, mx1 + mx2));
        return;
    }
    int mid = l + r >> 1;
    build(t[p].ls, l, mid), build(t[p].rs, mid + 1, r);
    pushup(p, l, r);
}
void modify(int p, int l, int r, int i) {
    if (l == r) {
        int x = rnk[l];
        int mx1 = hp[x].top(); hp[x].erase(mx1);
        int mx2 = hp[x].top(); hp[x].insert(mx1);
        if (col[x]) t[p].lmx = t[p].rmx = mx1, t[p].mx = mx1 + mx2;
        else t[p].lmx = t[p].rmx = max(0, mx1), t[p].mx = max(0, max(mx1, mx1 + mx2));
        return;
    }
    int mid = l + r >> 1;
    if (i <= mid) modify(t[p].ls, l, mid, i);
    else modify(t[p].rs, mid + 1, r, i);
    pushup(p, l, r);
}

int main() {
    ios::sync_with_stdio(0), cin.tie(0);
    cin >> n;
    for (int i = 1; i < n; i++) {
        int u, v, w; cin >> u >> v >> w;
        e[u].push_back({v, w}), e[v].push_back({u, w});
    }
    dfs1(1, 0), dfs2(1, 1);
    for (int i = n; i; i--) {
        int x = rnk[i];
        if (x != top[x]) continue;
        build(rt[x], dfn[x], dfn[x] + len[x] - 1);
        ans.insert(t[rt[x]].mx);
    }
    int m, cnt = n; cin >> m;
    while (m--) {
        char ch; cin >> ch;
        if (ch == 'A') {
            if (!cnt) cout << "They have disappeared.\n";
            else cout << ans.top() << '\n';
            continue;
        }
        int x; cin >> x; col[x] ^= 1;
        if (!col[x]) cnt++; else cnt--;
        while (x) { 
            int tp = top[x];
            ans.erase(t[rt[tp]].mx);
            if (fa[tp]) hp[fa[tp]].erase(t[rt[tp]].lmx + dep[tp] - dep[fa[tp]]);
            modify(rt[tp], dfn[tp], dfn[tp] + len[tp] - 1, dfn[x]);
            if (fa[tp]) hp[fa[tp]].insert(t[rt[tp]].lmx + dep[tp] - dep[fa[tp]]);
            ans.insert(t[rt[tp]].mx);
            x = fa[tp];
        }
    }
    return 0;
}