5.3 置信区间
前言
点估计无法提供其估计的误差,而区间估计可以。
案例:“某人的月薪比2k多,比20k少”,这就是一个区间估计。
区间估计的好坏有两个衡量指标:
- 区间长度
- 真实值落在该区间的概率
我们希望区间长度足够小,而真实值落在该区间的概率又足够大。
事实上,这两个指标是矛盾的,如果概率很大,会导致区间变大;如果区间长度变小,落在区间内的概率就会变小。
定义
\[P\{\underline{\theta}<\theta<\overline{\theta}\}=1-\alpha \]- \(\theta\)是要估计的参数。
- \((\underline{\theta},\overline{\theta})\)是置信区间,其中\(\underline{\theta}\)是置信下限,\(\overline{\theta}\)是置信上限。
- \(1-\alpha\)是置信水平,或者叫置信度。
做题的时候一般是题目告知置信度,然后需要求解置信上下限。
表述
\((\underline\theta,\overline\theta)\)能套住\(\theta\)的概率是\(1-\alpha\)。
这里需要区分两种表述:
- \((\underline\theta,\overline\theta)\)能套住\(\theta\)的概率是\(1-\alpha\)。
- \(\theta\) 落在 \((\underline\theta,\overline\theta)\)的概率是\(1-\alpha\)。
需要明确的是,\(\theta\)虽然是未知的,但是是确定的。\(\theta\)准确地固定在数轴上的一个位置,只是我们不知道在哪里。我们使用区间\((\underline\theta,\overline\theta)\)来做多次试验,每次试验的区间是随机的不同的,因此\(\theta\)有时会被区间套住,有时候不会。
因此,我们使用的表述是套住,而不是落在。后者是针对不确定的值时候的表述。
枢轴变量
定义
为了求解置信区间,需要构造枢轴变量
\[I=I(T,\theta) \]其中\(\theta\)是未知参数,\(T\)是已知的,\(I\) 的分布已知且与\(\theta\)无关。
对于给定的\(1-\alpha\),确定\(F\)的上\(\frac{\alpha}{2}\)分位数,记为\(u_{\frac{\alpha}{2}}\);确定\(F\)的上\((1-\frac{\alpha}{2})\)分位数,记为\(u_{1-\frac{\alpha}{2}}\),那么就会有
\[P\{u_{1-\frac{\alpha}{2}}<I(T,\theta)<u_{\frac{\alpha}{2}}\}=1-\alpha \]图解
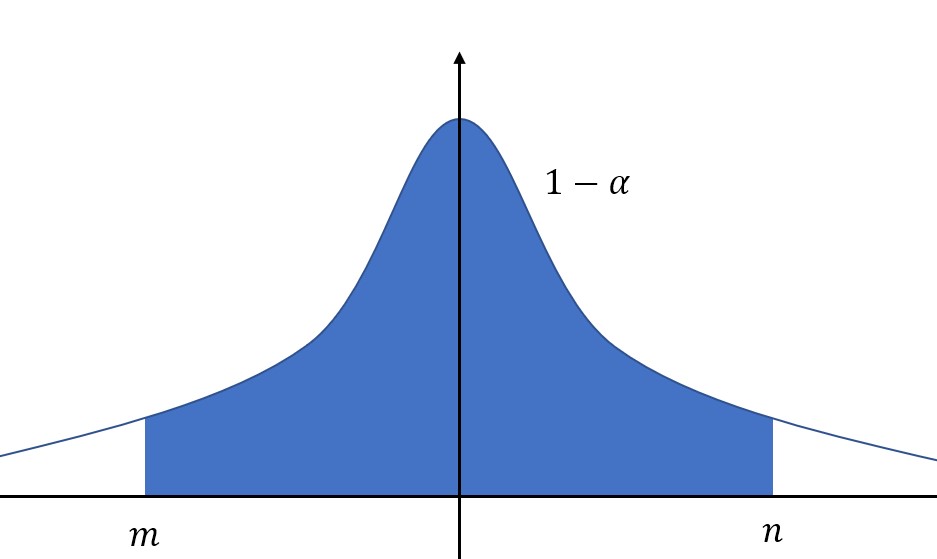
对于给定的置信度,也就是概率\(1-\alpha\),我们的目的是求解区间上下限,也就是图中的\(m\)和\(n\)。
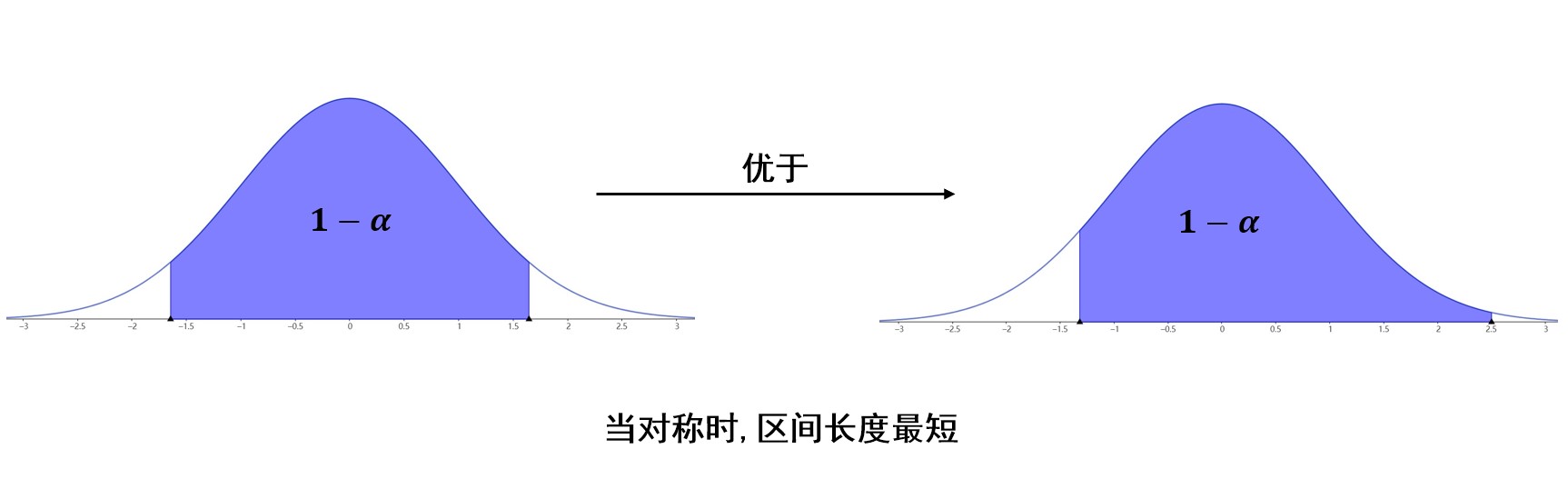
值得注意的是,我们希望区间长度小一些,如果研究的分布是正态分布,或者密度函数类似于上图,那么在置信度一定的情况下,即图中蓝色区域面积一定,只要选定区间位于中间,关于\(y\)轴对称,那么区间长度就是最小的。(因为峰值在中间)
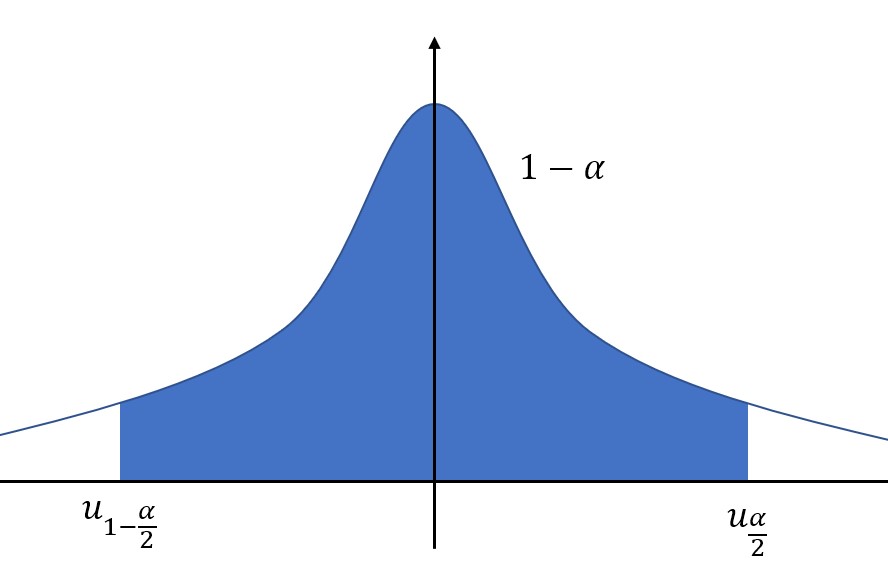
当置信区间位于中间时,置信度为\(1-\alpha\),那么左右两个置信上下限就可以通过上侧分位数表示了。
中间的阴影面积为\(1-\alpha\),那么左右两侧的空白面积就分别是\(\frac{\alpha}{2}\)。
置信上限使用上侧分位数表示就是:\(u_{\frac{\alpha}{2}}\).
置信下限使用上侧分位数表示就是:\(u_{1-\frac{\alpha}{2}}\).
总结
构造枢轴变量的目的是为了求解置信区间,将枢轴变量构造成我们熟悉的分布,比如正态分布,\(t\)分布,\(F\)分布。然后就可以利用这些分布的性质列出不等式,然后求解出我们要估计的参数的区间。
需要注意的是,枢轴变量只能包含一个未知的参数,即我们要估计的参数\(\theta\),只有这样才能进行不等式化简。
正态总体参数的置信区间
均值\(\mu\)的置信区间
情况1:方差\(\sigma^2\)已知
总体方差\(\sigma^2\)已知,估计\(\mu\),此时\(\mu\)是未知参数。
构造枢轴量:
\[U=\frac{\overline{X}-\mu}{\sigma/\sqrt{n}}\sim N(0,1) \]相关知识点:
标签:置信区间,5.3,frac,mu,数理统计,alpha,theta,sigma From: https://www.cnblogs.com/feixianxing/p/confidence-interval.html