[LeetCode] 1824. Minimum Sideway Jumps

There is a 3 lane road of length n that consists of n + 1 points labeled from 0 to n. A frog starts at point 0 in the second lane and wants to jump to point n. However, there could be obstacles along the way.

You are given an array obstacles of length n + 1 where each obstacles[i] (ranging from 0 to 3) describes an obstacle on the lane obstacles[i] at point i. If obstacles[i] == 0, there are no obstacles at point i. There will be at most one obstacle in the 3 lanes at each point.

• For example, if obstacles[2] == 1, then there is an obstacle on lane 1 at point 2.

The frog can only travel from point i to point i + 1 on the same lane if there is not an obstacle on the lane at point i + 1. To avoid obstacles, the frog can also perform a side jump to jump to another lane (even if they are not adjacent) at the same point if there is no obstacle on the new lane.

• For example, the frog can jump from lane 3 at point 3 to lane 1 at point 3.

Return the minimum number of side jumps the frog needs to reach any lane at point n starting from lane 2 at point 0.

Note: There will be no obstacles on points 0 and n.

Example 1:

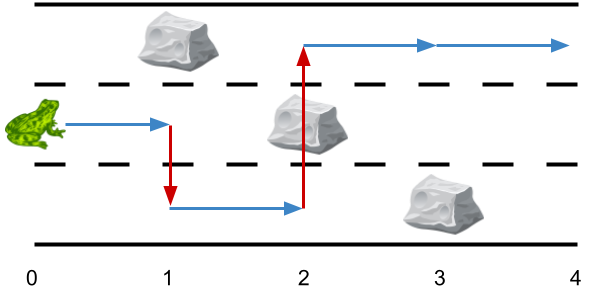
Input: obstacles = [0,1,2,3,0]
Output: 2 
Explanation: The optimal solution is shown by the arrows above. There are 2 side jumps (red arrows).
Note that the frog can jump over obstacles only when making side jumps (as shown at point 2).

Example 2:

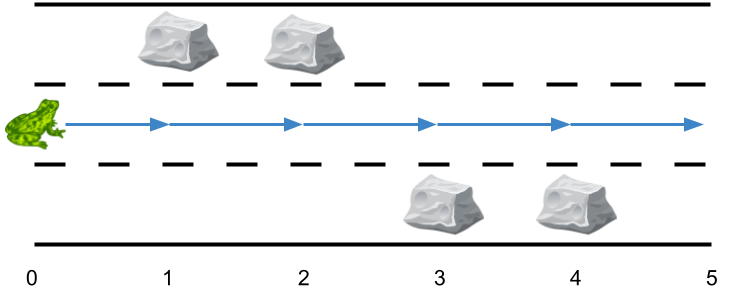
Input: obstacles = [0,1,1,3,3,0]
Output: 0
Explanation: There are no obstacles on lane 2. No side jumps are required.

Example 3:

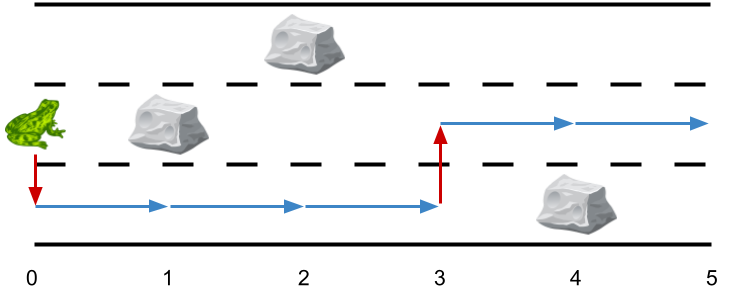
Input: obstacles = [0,2,1,0,3,0]
Output: 2
Explanation: The optimal solution is shown by the arrows above. There are 2 side jumps.

Constraints:

• obstacles.length == n + 1
• 1 <= n <= 5 * 105
• 0 <= obstacles[i] <= 3
• obstacles[0] == obstacles[n] == 0

最少侧跳次数。

给你一个长度为 n 的 3 跑道道路 ，它总共包含 n + 1 个 点 ，编号为 0 到 n 。一只青蛙从 0 号点第二条跑道 出发 ，它想要跳到点 n 处。然而道路上可能有一些障碍。

给你一个长度为 n + 1 的数组 obstacles ，其中 obstacles[i] （取值范围从 0 到 3）表示在点 i 处的 obstacles[i] 跑道上有一个障碍。如果 obstacles[i] == 0 ，那么点 i 处没有障碍。任何一个点的三条跑道中 最多有一个 障碍。

比方说，如果 obstacles[2] == 1 ，那么说明在点 2 处跑道 1 有障碍。
这只青蛙从点 i 跳到点 i + 1 且跑道不变的前提是点 i + 1 的同一跑道上没有障碍。为了躲避障碍，这只青蛙也可以在 同一个 点处 侧跳 到 另外一条 跑道（这两条跑道可以不相邻），但前提是跳过去的跑道该点处没有障碍。

比方说，这只青蛙可以从点 3 处的跑道 3 跳到点 3 处的跑道 1 。
这只青蛙从点 0 处跑道 2 出发，并想到达点 n 处的 任一跑道 ，请你返回 最少侧跳次数 。

注意：点 0 处和点 n 处的任一跑道都不会有障碍。

来源：力扣（LeetCode）
链接：https://leetcode.cn/problems/minimum-sideway-jumps
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

思路是动态规划。我们需要一个长度为 3 的数组，分别表示三条跑道，记录到达 dp[i][j] 位置的时候，最小花费是多少。i 表示走到哪一个点了，j 表示在哪一条赛道上。由于走到当前位置只和上一个位置有关，我们可以精简为一维数组。

初始化的时候，因为青蛙是在第二条跑道，跳到隔壁的跑道是有花费的，所以 dp[0] = dp[2] = 1，dp[1] = 0。开始走了之后，看一下当前赛道是否有障碍物，如果没有，则走到当前 i 位置的花费跟上一个位置 i - 1 相同；如果当前位置有障碍，则看一下是否从别的赛道跳过来的花费会更小。

时间O(n)

空间O(1) - 长度只有3的数组

Java实现

 1 class Solution {
 2     public int minSideJumps(int[] obstacles) {
 3         int n = obstacles.length;
 4         int[] dp = new int[3];
 5         // 初始化的时候，0和2位置都是1，因为跳过去会有花费
 6         dp[0] = dp[2] = 1;
 7         for (int i = 1; i < n; i++) {
 8             int object = obstacles[i];
 9             int pre0 = dp[0];
10             int pre1 = dp[1];
11             int pre2 = dp[2];
12             // 注意这里如果填Integer.MAX_VALUE，后面取更小值的时候就不对了
13             Arrays.fill(dp, (int) 2e9);
14 
15             // 如果当前位置无障碍物，那么花费跟上一个位置一样
16             if (object != 1)
17                 dp[0] = pre0;
18             if (object != 2)
19                 dp[1] = pre1;
20             if (object != 3)
21                 dp[2] = pre2;
22             
23             // 看看从隔壁位置跳过来，最小花费是多少
24             if (object != 1)
25                 dp[0] = Math.min(dp[0], Math.min(dp[1], dp[2]) + 1);
26             if (object != 2)
27                 dp[1] = Math.min(dp[1], Math.min(dp[0], dp[2]) + 1);
28             if (object != 3)
29                 dp[2] = Math.min(dp[2], Math.min(dp[0], dp[1]) + 1);
30         }
31         return Math.min(dp[0], Math.min(dp[1], dp[2]));
32     }
33 }

LeetCode 题目总结