相机模型P矩阵
公式:
\[P = KR[I | -C^{\backsim}] \]其中\(C^{\backsim}\)表示平移矩阵 为齐次坐标 即世界坐标系原点到相机坐标系原点的距离 \(R\)同样表达的也是这个关系。
也写成这种形式:
\[P = M[I | M^{-1}p_4] \]其中\(M = KR\),\(p_4\)为P的第四列
如果\(M\)矩阵不可逆时 为无穷远相机
原文对相机中心点坐标的描述:

相机模型P矩阵分解
行向量
\[P = \begin{bmatrix} p_{11} & p_{12} & p_{13} & p_{14} \\ p_{21} & p_{22} & p_{23} & p_{24} \\ p_{31} & p_{32} & p_{33} & p_{34} \\ p_{41} & p_{42} & p_{43} & p_{44} \\ \end{bmatrix} = \begin{bmatrix}P^{1T} \\ P^{2T} \\ P^{3T} \\ \end{bmatrix} \]\(P^{3T}\)为主平面 通过相机光心点并且平行于相机成像平面 \(P^{2T}\)通过相机光心点和成像平面的X轴 另一个同理
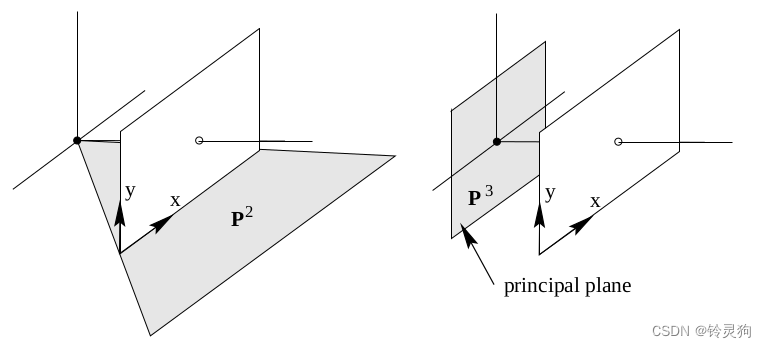
列向量
\[P = \begin{bmatrix} p_{11} & p_{12} & p_{13} & p_{14} \\ p_{21} & p_{22} & p_{23} & p_{24} \\ p_{31} & p_{32} & p_{33} & p_{34} \\ p_{41} & p_{42} & p_{43} & p_{44} \\ \end{bmatrix} = \begin{bmatrix}P_{1} & P_{2} & P_{3} & P_{4} \\ \end{bmatrix} \]\(P_{1}\)为世界坐标系X轴的消影点 x轴方向为\(D = (1, 0, 0, 0)^T\) 所以\(P_{1} = PD\)
同理\(P_{2}\)为世界坐标系Y轴的消影点
\(P_{3}\)为世界坐标系Z轴的消影点
\(P_{4}\)为世界坐标系原点的图像点 \(P_{4} = P(0, 0, 0, 1)^T\)
消影点投影
设消影点的齐次坐标为\(D = (d^T, 0)\) 则消影点映射到成像平面的公式为:
\[x = PD = [M | p_4]D \]但是此时D的最后一维为0 所以\(p_4\)相当于没有计算(很容易推)所以结果为:
\[x = Md \]可见消影点投影只与M有关 与相机的位置无关
点的深度问题
\[x = \omega(x, y, 1)^T = PX \]\(\omega\)其实为三维点原深度 也可以解释为从相机中心到三维空间点的射线与主轴方向的点积。 \((x, y, 1)\)在第三维只有深度的体现 所以可以单独求出深度:
\[\omega = P^{3T}X = P^{3T}(X - C) = m^{3T}(X^{\backsim} - C^{\backsim}) \]其中C为相机中心 PC = 0 所以随便加
另外从齐次到非齐次 丢掉了最后一个维度 所以P相应也舍去最后一个维度 又因为前面是\(M[I | t]\)最后一个维度t干掉后 只剩\(M * I\) 所以等于M矩阵的第三行 即\(m^{3T}\)
主点与主轴方向
主轴即通过相机光心 并且垂直于主平面的轴 主轴和成像平面的交点称为主点
已知主平面和主平面的法向量 讲主平面的法向量写成无穷远点的形式:
经过相机的任何一条射线 与像平面的交点可以表示为:\(PD\) 这个也等价于这个点的无穷远点在像平面的投影 P是3 * 4 D要求是 4 * 1嘛 最后一维就是0 已知三维点非齐次坐标 变成无穷远点的齐次坐标只需在最后一维添加0即可
所以主点即为主平面的法向量的无穷远点形式在像平面的投影
\[P_{main} = PP_{infine} = [M | p_4]P_{infine} \]然后干掉第四维 和上面的消影点投影那里一样 \(p_4\)就不参与运算了:
\[P_{main} = M P_{infine} = Mm^{3T} \]等于M和他自己的第三行相乘 此处很容易推导顺出来 其中\(m^{3T}\)被称为主轴方向
对极线区分有限相机和无穷远相机
有限相机的所有对极线都会相交于一点 这一点即一个相机的光心在另一个相机的像平面成像的位置。
对于无穷远相机的话 主平面即无穷远平面 所有的对极线也相交 但是交点在无穷远平面 即相交于无穷远点 所以对极线是平行的。
根据相机参数计算相机内参

原作者链接:传送门