题目选讲
\(\text{By DaiRuiChen007}\)
I. [洛谷 4637] - 扫雷机器人
思路分析
考虑求出期望的过程:
- 每种引爆地雷的顺序,共有 \(n!\) 种情况
- 对于每种顺序,计算出其中实际引爆的地雷个数,也就是所有没有在之前被引爆的地雷个数
- 将每种方案中实际引爆的地雷个数当成操作次数,乘上概率 \(\dfrac1{n!}\),求和计算期望
由于期望具有线性性,所以我们可以考虑计算每个地雷对答案的贡献,也就是说,对于每个地雷,求出其会在多少种方案中被实际引爆
求出所有可以导致第 \(i\) 个地雷被引爆(直接或间接)的地雷集合,设为 \(\mathbf S_i\),那么 \(i\) 第一个被引爆,当且仅当所有 \(\mathbf S_i\) 中的地雷都在 \(i\) 之后被引爆,
所以问题就转化成了:对于第 \(i\) 个元素,求出在所有排列中,满足 \(i\) 是 \(\mathbf S_i\) 中所有元素里的第一个的情况总数
由于其他的元素在哪里并不重要,所以我们只需要考虑 \(\mathbf S_i\) 中的元素之间的相对关系,不难得到满足 \(i\) 恰好是其中第一个数的方案数占所有方案数的比例为:\(\dfrac{(|\mathbf S_i|-1)!}{|\mathbf S_i|!}=\dfrac{1}{|\mathbf S_i|}\),因此在所以排列中,第 \(i\) 颗地雷被实际引爆的次数应该是 \(\dfrac{n!}{|\mathbf S_i|}\) 次,这也是第 \(i\) 颗地雷对答案的贡献
套用期望的计算公式可以得到:
\[\begin{aligned} \text{Answer} &=\dfrac{1}{n!}\sum_{i=1}^n\dfrac{n!}{|\mathbf S_i|}\\ &=\sum_{i=1}^n\dfrac1{|\mathbf S_i|} \end{aligned} \]所以问题就转化成求所有的 \(|\mathbf S_i|\)
可以将所有地雷向其能够直接引爆的点连一条边,我们需要求出对于每个点 \(i\),有多少个点能够到达 \(i\)
考虑缩点,在 DAG 上做拓扑排序转移一个用 bitset 维护的 \(\mathbf S_i\) 即可
注意:如果我们直接在原图上做 \(n\) 次 BFS,复杂度在完全图上会退化到 \(\Theta(n^3)\)
时间复杂度 \(\Theta(n^2)\)
代码呈现
#include<bits/stdc++.h>
using namespace std;
const int MAXN=4001;
int p[MAXN],d[MAXN];
vector <int> edge[MAXN],g[MAXN];
bool vis[MAXN];
bitset <MAXN> f[MAXN];
int low[MAXN],dfn[MAXN],dfncnt,sk[MAXN],siz[MAXN],bel[MAXN],deg[MAXN],top,scc;
bool ins[MAXN],link[MAXN][MAXN];
inline void tarjan(int p) {
low[p]=dfn[p]=++dfncnt;
ins[p]=true; sk[++top]=p;
for(int v:edge[p]) {
if(!dfn[v]) {
tarjan(v);
low[p]=min(low[p],low[v]);
} else if(ins[v]) low[p]=min(low[p],low[v]);
}
if(low[p]==dfn[p]) {
++scc;
int k;
do {
k=sk[top--];
bel[k]=scc;
f[scc].set(k);
++siz[scc];
ins[k]=false;
} while(k!=p);
}
}
signed main() {
int n;
scanf("%d",&n);
for(int i=1;i<=n;++i) scanf("%d%d",&p[i],&d[i]);
for(int i=1;i<=n;++i) {
for(int j=1;j<=n;++j) {
if(abs(p[i]-p[j])<=d[i]) {
edge[i].push_back(j);
}
}
}
for(int i=1;i<=n;++i) if(!dfn[i]) tarjan(i);
for(int i=1;i<=n;++i) {
for(int j:edge[i]) {
if(bel[i]==bel[j]||link[bel[i]][bel[j]]) continue;
g[bel[i]].push_back(bel[j]);
link[bel[i]][bel[j]]=true;
++deg[bel[j]];
}
}
queue <int> q;
for(int i=1;i<=scc;++i) {
if(!deg[i]) {
q.push(i);
}
}
while(!q.empty()) {
int p=q.front();
q.pop();
for(int v:g[p]) {
f[v]|=f[p];
--deg[v];
if(!deg[v]) q.push(v);
}
}
double res=0;
for(int i=1;i<=n;++i) res+=1.0/((int)f[bel[i]].count());
printf("%.4lf\n",res);
return 0;
}
II. [洛谷 4649] - 训练路径
思路分析
反面考虑,计算最多能加几条非树边使图上没有偶环
如果某条非树边 \((u,v)\) 添加后使得 \(u\to \operatorname{LCA}(u,v)\to v\to u\) 的长度为偶数,则不能必选择 \((u,v)\)
只考虑添加 \((u,v)\) 使得 \(u\to \operatorname{LCA}(u,v) \to v\to u\) 的长度为奇数的边 \((u,v)\)
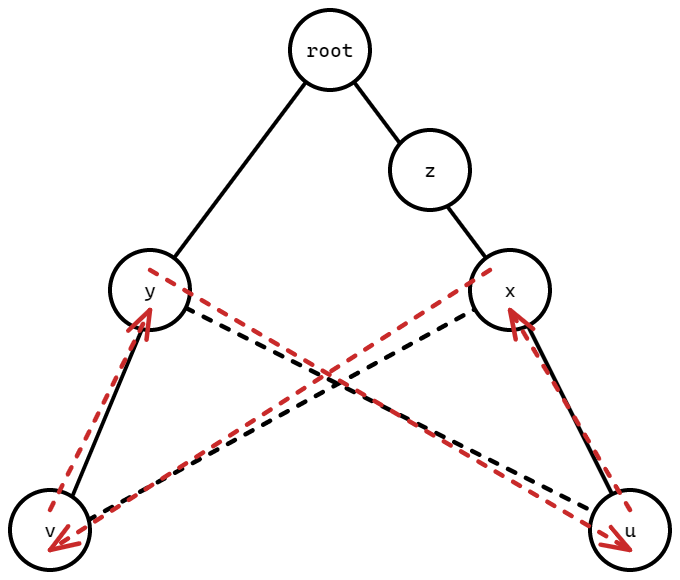
如果两条边 \((u,v)\) 和 \((x,y)\) 的树上路径有交集,如下图所示,也会形成一个偶环:
所以我们的目标就是在树上选择若干条不相交的非树边使得其权值和最大
考虑在添加某条非树边 \((u,v)\) 后把 \(u\to v\) 的所有边都删掉,然后分成若干棵子树进行 dp
我们把每条非树边 \((u,v)\) 在 \(\operatorname{LCA}(u,v)\) 处考虑,设 \(dp_{p,\mathbf S}\) 表示以 \(u\) 为根的子树,且 \(p\) 到集合 \(\mathbf S\)(状态压缩)中的儿子的边已经被删掉后能选择的最优答案
那么对于一条路径 \((u,v)\) 满足 \(\operatorname{LCA}(u,v)=p\) 他能带来的价值为:
\[value(u,v)=w(u,v)+\sum_{x\in path(u,v)}^{fa(x)\neq p,x\neq p} dp_{fa(x),\{x\}} \]设 \(u\to v\) 的路径包含 \(x\to p\to y\) 且 \(x,y\) 均为 \(p\) 的儿子,我们可以用用这个价值去转移:
\[\forall \mathbf S:x,y\not\in \mathbf S\\ dp_{p,S}\gets value(u,v)+dp_{p,\mathbf S\cup\{x,y\}} \]最终的答案为 \(\sum w(u,v)-dp_{1,\varnothing}\)
时间复杂度 \(\Theta(m\log n+n2^{|\mathbf S|})\)
代码呈现
#include<bits/stdc++.h>
using namespace std;
const int MAXN=1001;
vector <int> tree[MAXN];
struct node {
int src,des,val;
};
vector <node> vec,link[MAXN];
int dep[MAXN],fa[MAXN],siz[MAXN],son[MAXN],root[MAXN],fid[MAXN];
int dp[MAXN][1<<10];
inline int bit(int x) {
return 1<<x;
}
inline void init1(int p,int f) {
fa[p]=f,siz[p]=1,dep[p]=dep[f]+1;
for(int v:tree[p]) {
if(v==f) continue;
init1(v,p);
siz[p]+=siz[v];
if(siz[v]>siz[son[p]]) son[p]=v;
}
}
inline void init2(int p,int r) {
root[p]=r;
if(son[p]) init2(son[p],r);
for(int v:tree[p]) {
if(v==son[p]||v==fa[p]) continue;
init2(v,v);
}
}
inline void init3(int p) {
for(int i=0;i<tree[p].size();++i) {
int v=tree[p][i];
if(v==fa[p]) continue;
fid[v]=bit(i);
init3(v);
}
}
inline int LCA(int u,int v) {
while(root[u]!=root[v]) {
if(dep[root[u]]<dep[root[v]]) swap(u,v);
u=fa[root[u]];
}
return dep[u]>dep[v]?v:u;
}
inline void dfs(int p) {
for(int v:tree[p]) {
if(v==fa[p]) continue;
dfs(v);
}
for(int s=0;s<bit(tree[p].size());++s) {
for(int i=0;i<tree[p].size();++i) {
if(!((s>>i)&1)) dp[p][s]+=dp[tree[p][i]][0];
}
}
for(auto e:link[p]) {
int val=e.val,u=0,v=0;;
if(e.src!=p) {
val+=dp[e.src][0];
for(u=e.src;fa[u]!=p;u=fa[u]) val+=dp[fa[u]][fid[u]];
}
if(e.des!=p) {
val+=dp[e.des][0];
for(v=e.des;fa[v]!=p;v=fa[v]) val+=dp[fa[v]][fid[v]];
}
int t=fid[u]|fid[v];
for(int s=0;s<bit(tree[p].size());++s) {
if(!(s&t)) dp[p][s]=max(dp[p][s],val+dp[p][s|t]);
}
}
}
signed main() {
int n,m,res=0;
scanf("%d%d",&n,&m);
for(int i=1;i<=m;++i) {
int u,v,w;
scanf("%d%d%d",&u,&v,&w);
if(!w) {
tree[u].push_back(v);
tree[v].push_back(u);
} else {
res+=w;
vec.push_back((node){u,v,w});
}
}
init1(1,0);
init2(1,1);
init3(1);
for(auto e:vec) {
int lca=LCA(e.src,e.des);
if(!((dep[e.src]+dep[e.des]-dep[lca]*2)&1)) link[lca].push_back(e);
}
dfs(1);
printf("%d\n",res-dp[1][0]);
return 0;
}
III. [CodeForces Gym 104090H] - RPG Pro League
思路分析
按顺序把原问题依次解决如下的子问题:
1. 计算最多能够构成多少支队伍
假设我们知道构成的队伍数量 \(k\),先考虑如何判断是否存在合法的组队方案
考虑对于每个队伍拆成四个位置,一个 D 角色,一个 S 角色,一个 B 角色,一个 D 或 S 角色
然后连边就按每个人能胜任的位置进行连边即可,这样能够构造一张二分图
只要判断这个二分图上是否存在大小为 \(4\times k\) 的匹配即可
不过这样的点集和边集大小都显然过大,考虑优化复杂度
我们发现每个人所对应信息其实很少,可以用一个 \(3\) 位二进制数表示,即:该选手能否作为 D 角色或 S 角色或 B 角色,由于每个选手至少扮演一种角色,因此有效的二进制数范围为 \(1\sim 7\)
因此我们可以把 \(n\) 个右部点压缩成 \(7\) 种本质不同的右部点,而每种右部点对于组队数量的贡献都是一致的
同理,对于每支队伍其需求也是相同的,那么我们可以把 \(4\times k\) 个左部点压缩成 \(4\) 个本质不同的左部点
接下来考虑如何判定图上是否存在大小为 \(4\times k\) 的匹配
考虑用 Hall 定理判断,对于左部点的每个子集计算其邻域的大小并进行比较即可
事实上,这是 Hall 定理的一种推广,较详细的讲解和证明可以参看这篇文章(加强 2 部分)
因此我们能够得到一种在 \(\Theta(1)\) 复杂度内计算出某个给定的选手集合能否匹配出 \(k\) 支队伍的判定方法
先令右部点集为参赛选手的全集,用二分或者增量算法都可以得到最多能够构成多少支队伍
我们能够证明,无论如何修改每个人的费用,最多的队伍数量也不会改变,因此队伍数量可以看成定值
2. 考虑如何求出初始的最小费用
事实上可以考虑如下的一个贪心:
按每个人的费用从多到少排序,如果删去某个选手不影响构成队伍数量,就优先删掉这个选手
关于这个贪心正确性的证明需要拟阵相关的知识,在这里略过
那么从大到小依次考虑每个选手是否不被需要即可
3. 考虑如何处理每次修改的操作
先假设修改的 \(x\) 在原来的最优的方案中
用拟阵相关的性质,我们能够得到如下的结论:
在修改 \(x\) 的权值之后,新的最优解一定是删去 \(x\) 并加入某个选手,或者不操作
这个证明和对偶拟阵有关,在这里同样省略
因此我们用 set 维护 \(7\) 种选手中没被选中的选手中费用最小的,判断是否能够保证组队数量不变,求出所有选手中花费最小的一个放进去(如果都不行就把 \(x\) 放回去)
同理,如果修改的 \(x\) 不在原来的最优方案中,那么最优解一定是用 \(x\) 替换某个已经被选的选手
我们用 set 维护 \(7\) 种选手中被选中的选手中费用最大的,同样判断替换是否可行即可
综上,我们用 set 来维护选手的权值,就能够得到 \(\Theta((n+q)\log n)\) 的总时间复杂度
代码呈现
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int MAXN=1e5+1;
struct node {
int val,id;
node() { val=id=0; }
node(int _val,int _id) { val=_val,id=_id; }
inline friend bool operator <(const node &A,const node &B) {
if(A.val==B.val) return A.id<B.id;
return A.val>B.val;
}
} a[MAXN];
int n,q,role[MAXN],price[MAXN],res,sum,cnt[8];
bool inq[MAXN];
multiset <node> in[8],out[8]; //选的点和没选的点的权值
const int nbh[16]={0,170,204,238,240,250,252,254,238,238,238,238,254,254,254,254}; //左部点集邻域
const int siz[16]={0,1,1,2,1,2,2,3,1,2,2,3,2,3,3,4}; //左部点集大小
inline int bit(int x) { return 1<<x; }
inline int count(int S) {
int ret=0;
for(int i=1;i<8;++i) if(S&bit(i)) ret+=cnt[i];
return ret;
}
inline bool check() {
for(int A=1;A<16;++A) if(count(nbh[A])<siz[A]*res) return false;
return true;
}
signed main() {
ios::sync_with_stdio(false);
cin.tie(nullptr),cout.tie(nullptr);
cin>>n;
for(int i=1;i<=n;++i) {
string str;
cin>>str>>price[i];
for(char ch:str) {
if(ch=='D') role[i]|=bit(0);
if(ch=='S') role[i]|=bit(1);
if(ch=='B') role[i]|=bit(2);
}
sum+=price[i];
++cnt[role[i]],inq[i]=true;
a[i]=node(price[i],i);
in[role[i]].insert(a[i]);
}
while(true) {
++res;
if(!check()) break;
}
--res; //最大匹配
sort(a+1,a+n+1);
for(int i=1;i<=n;++i) {
int state=role[a[i].id];
--cnt[state];
if(check()) {
out[state].insert(a[i]);
sum-=a[i].val,inq[a[i].id]=false;
//从权值大的开始,能删则删
}
else ++cnt[state];
}
for(int k=1;k<8;++k) for(auto x:out[k]) in[k].erase(in[k].find(x));
cin>>q;
while(q--) {
int x,cost;
cin>>x>>cost;
if(inq[x]) {
sum-=price[x];
in[role[x]].erase(in[role[x]].find(node(price[x],x)));
inq[x]=false;
price[x]=cost;
--cnt[role[x]];
out[role[x]].insert(node(price[x],x));
//更新,先删除
int pos=x;
for(int k=1;k<8;++k) {
if(out[k].empty()) continue;
int y=out[k].rbegin()->id;
++cnt[role[y]];
if(check()&&price[y]<price[pos]) pos=y;
--cnt[role[y]];
//代价最小的能否替换
}
sum+=price[pos];
out[role[pos]].erase(out[role[pos]].find(node(price[pos],pos)));
in[role[pos]].insert(node(price[pos],pos));
inq[pos]=true;
++cnt[role[pos]];
//找最优的替换解
} else {
out[role[x]].erase(out[role[x]].find(node(price[x],x)));
price[x]=cost;
sum+=price[x];
in[role[x]].insert(node(price[x],x));
inq[x]=true;
++cnt[role[x]];
//更新,先加入
int pos=x;
for(int k=1;k<8;++k) {
if(in[k].empty()) continue;
int y=in[k].begin()->id;
--cnt[role[y]];
if(check()&&price[y]>price[pos]) pos=y;
++cnt[role[y]];
//代价最大的能否被替换
}
sum-=price[pos];
in[role[pos]].erase(in[role[pos]].find(node(price[pos],pos)));
out[role[pos]].insert(node(price[pos],pos));
inq[pos]=false;
--cnt[role[pos]];
//找最优的替换解
}
cout<<sum<<"\n";
}
return 0;
}
IV. [CF1672F] - Array Shuffling & Checker for Array Shuffling
Problem Link(F1) | Problem Link(F2)
思路分析
先考虑如何计算一个 \(\{a_i\}\) 的排列 \(\{b_i\}\) 的权值:对于个 \(i\),建立有向边 \(a_i\to b_i\),得到一张有向图 \(\mathbf G\)
定义 \(\operatorname{cyc}(\mathbf G)\) 表示 \(\mathbf G\) 的最大环拆分的大小,即把 \(\mathbf G\) 拆成尽可能多的环使得每条边都恰好在一个环中时拆分成环的数量
注意到如下的观察:
观察一:
\(\{b_i\}\) 的权值等于 \(n-\operatorname{cyc}(\mathbf G)\)
证明如下:
注意到交换 \((b_i,b_j)\) 等价于交换 \(a_i\to b_i\) 和 \(a_i\to b_j\) 的终点,我们的目标就是使得 \(\mathbf G\) 中产生 \(n\) 个环
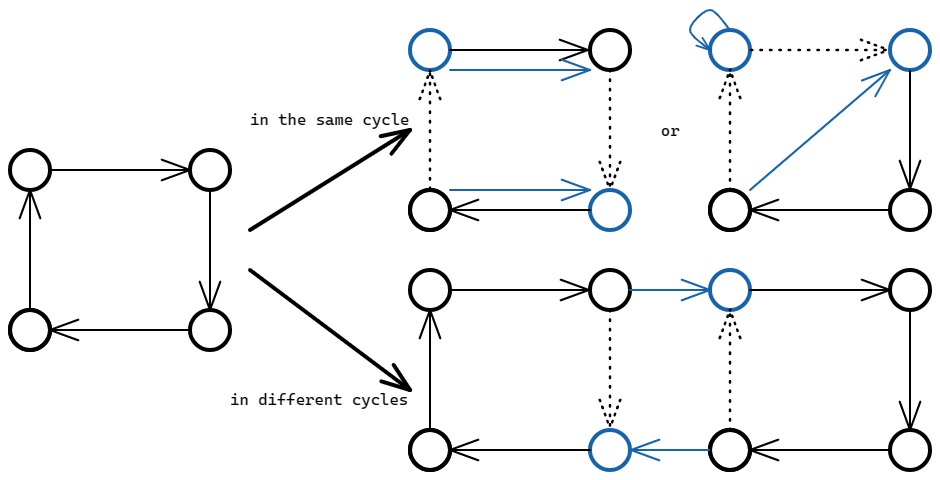
而一次操作可以根据 \(b_i,b_j\) 在 \(\operatorname{cyc(\mathbf G)}\) 对应的分解中分成是否在同一个环中的两种情况
由上图可得,只要 \(b_i,b_j\) 在同一个环中,无论如何 \(\mathbf G\) 中的环数会 \(+1\),而如果 \(b_i,b_j\) 不在同一个环中,那么 \(\mathbf G\) 中的环数一定会 \(-1\)
因此对于任意的大小为 \(k\) 的环分解,至少需要操作 \(n-k\) 次,而不断操作两个相邻的 \(b_i,b_j\) 给了我们一种操作 \(n-k\) 次的方法
综上所述,将 \(\{b_i\}\) 还原至少需要 \(n-\operatorname{cyc}(\mathbf G)\) 次操作
那么原问题就转化为了最小化 \(\operatorname{cyc}(\mathbf G)\) 的问题
记 \(cnt_x\) 为 \(x\) 在 \(\{a_i\}\) 中的出现次数
注意到如下的观察:
观察二:
对于所有 \(\mathbf G\) 和正整数 \(x\in [1,n]\),\(\operatorname{cyc}(\mathbf G)\ge cnt_{x}\)
事实上 \(cnt_x\) 等于 \(\mathbf G\) 中 \(x\) 的入度和出度,那么原命题可以等价于证明:
对于每个 \(\mathbf G\) 的最大环拆分,不存在一个环经过某个 \(x\) 两次
而根据最大环拆分的定义,经过 \(x\) 两次的环会在最大环拆分中拆成两个环,因此原命题得证
我们假设 \(\{a_i\}\) 中的众数 \(m\) 出现了 \(c\) 次,根据观察二,那么答案 \(\ge n-c\)
猜测答案 \(=n-c\),即我们需要构造一个 \(\mathbf G\) 使得 \(\operatorname{cyc}(\mathbf G)=c\)
考虑什么时候 \(\operatorname{cyc}(\mathbf G)=c\),注意到如下的观察:
观察三:
\(\operatorname{cyc}(\mathbf G)=c \iff \operatorname{cycle}(\mathbf G-\mathbf G_m)=0\) 其中 \(\operatorname{cycle}\) 定义为图中的环的数量,\(\operatorname{cycle}(\mathbf G-\mathbf G_m)=0\) 即在 \(\mathbf G\) 中删除 \(m\) 和所有与 \(m\) 相邻的边得到的新图 \(\mathbf G-\mathbf G_m\) 中不存在环
证明如下:
- 证 \(\operatorname{cyc}(\mathbf G)=c \implies \operatorname{cycle}(\mathbf G-\mathbf G_m)=0\):
考虑逆否命题 $\operatorname{cycle}(\mathbf G-\mathbf G_m)>0\implies \operatorname{cyc}(\mathbf G)>c $
那么考虑 \(\operatorname{cycle}(\mathbf G-\mathbf G_m)\) 中的一个环 \(\mathbf C\):在子图 \(\mathbf G-\mathbf C\) 中,最大的度(等价于众数的出现个数)依然是 \(c\),根据观察二,得到 \(\operatorname{cyc}(\mathbf G-\mathbf C)\ge c\)
所以 \(\operatorname{cyc}(\mathbf G)=\operatorname{cyc}(\mathbf G-\mathbf C)+1\ge c+1>c\)
2. 证 \(\operatorname{cycle}(\mathbf G-\mathbf G_m)=0\implies \operatorname{cyc}(\mathbf G)=c\)考虑逆否命题 \(\operatorname{cyc}(\mathbf G)>c \implies \operatorname{cycle}(\mathbf G-\mathbf G_m)>0\)
由于抽屉原理,在 \(\operatorname{cyc}(\mathbf G)\) 个环中必然至少有一个不经过 \(m\),那么这个环的存在会使得 \(\operatorname{cycle}(\mathbf G-\mathbf G_m)>0\)
因此我们能够解决 F2:对 \(\mathbf G-\mathbf G_m\) 进行拓扑排序,如果存在环说明不是最优解,否则是最优解
时间复杂度 \(\Theta(n)\)
接下来继续解决 F1:
构造出一个 \(\mathbf G\) 使得 \(\mathbf G\) 存在一个大小为 \(c\) 的环剖分是简单的:考虑第 \(i\) 个环中包含所有 \(cnt_x\ge i\) 的 \(x\),这样每个 \(x\) 会出现在 \(cnt_x\) 个环中
那么接下来就是确定每个环的方向使得 \(\mathbf G-\mathbf G_m\) 是一个 DAG
有这样的一个想法,在值域 \([1,n]\) 上构造一个偏序关系 \(\succeq\) 满足:
- 对于任意 \(i,j\in [1,n]\),\((i,j)\) 在 \(\succeq\) 的定义域中
- 对于所有 \(k\in [1,n],k\ne m\),\(m\succ k\) 成立,即 \(m=\max_\succeq\{1,2,3,\cdots,n\}\)
那么对于每个环,我们将每个点按 \(\succeq\) 的顺序排序,然后从大到小连边,最小的一定会连到 \(m\) 处
此时如果删去 \(m\),剩下的所有边的方向与 \(\succeq\) 的方向相同,那么这样的图一定是 DAG
此处取偏序关系 \(\succeq\) 等价于按 \(cnt_x\) 为第一关键字,\(x\) 为第二关键字从大到小排序,\(m\) 为最大的众数
时间复杂度 \(\Theta(n\log n)\)
代码呈现
[CF1672F1] - Array Shuffling
#include<bits/stdc++.h>
using namespace std;
const int MAXN=2e5+1;
int a[MAXN],cnt[MAXN];
vector <int> buc[MAXN];
inline bool cmp(const int &id1,const int &id2) {
if(cnt[a[id1]]==cnt[a[id2]]) return a[id1]>a[id2];
return cnt[a[id1]]>cnt[a[id2]];
}
inline void solve() {
int n;
scanf("%d",&n);
for(int i=1;i<=n;++i) buc[i].clear(),cnt[i]=0;
for(int i=1;i<=n;++i) {
scanf("%d",&a[i]);
++cnt[a[i]];
buc[cnt[a[i]]].push_back(i);
}
for(int i=1;i<=n;++i) {
sort(buc[i].begin(),buc[i].end(),cmp);
for(int j=1;j<(int)buc[i].size();++j) swap(a[buc[i][j-1]],a[buc[i][j]]);
}
for(int i=1;i<=n;++i) printf("%d ",a[i]);
puts("");
}
signed main() {
int T;
scanf("%d",&T);
while(T--) solve();
return 0;
}
[CF1672F2] - Checker for Array Shuffling
// LUOGU_RID: 98400367
#include<bits/stdc++.h>
using namespace std;
const int MAXN=2e5+1;
int a[MAXN],b[MAXN],cnt[MAXN],deg[MAXN];
vector <int> G[MAXN];
inline void solve() {
int n,u=1;
scanf("%d",&n);
for(int i=1;i<=n;++i) deg[i]=0,cnt[i]=0,G[i].clear();
for(int i=1;i<=n;++i) scanf("%d",&a[i]),++cnt[a[i]];
for(int i=1;i<=n;++i) scanf("%d",&b[i]);
for(int i=1;i<=n;++i) if(cnt[a[i]]>cnt[a[u]]) u=i;
for(int i=1;i<=n;++i) {
if(a[i]==a[u]||b[i]==a[u]) continue;
G[a[i]].push_back(b[i]);
++deg[b[i]];
}
queue <int> q;
for(int i=1;i<=n;++i) if(!deg[i]) q.push(i);
while(!q.empty()) {
int p=q.front(); q.pop();
for(int v:G[p]) {
--deg[v];
if(!deg[v]) q.push(v);
}
}
for(int i=1;i<=n;++i) {
if(deg[i]) {
puts("WA");
return ;
}
}
puts("AC");
}
signed main() {
int T;
scanf("%d",&T);
while(T--) solve();
return 0;
}
V. [CF1526D] - Kill Anton
思路分析
记 \(S-S_i\) 为 \(S\) 中删除 \(S_i\) 后得到的字符串,记 \(|S|=n\)
首先考虑在给定了 \(S\) 和 \(T\) 的情况下如何计算 \(T\) 到 \(S\) 的距离,记为 \(\operatorname{dist}(S,T)\),注意到如下的观察:
观察一:
\(\operatorname{dist}\) 满足对于任意字符串 \(A,B,C\) 满足 \(|A|=|B|=|C|\) 均有 \(\operatorname{dist}(A,C)\le\operatorname{dist}(A,B)+\operatorname{dist}(B,C)\)
证明很简单,考虑 \(\operatorname{dist}(A,C)\) 的实际意义,即 \(A\gets C\) 的最少操作次数,而 \(\operatorname{dist}(A,B)+\operatorname{dist}(B,C)\) 则表示了 \(A\gets B\gets C\) 的一种操作方案,其代价为 \(\operatorname{dist}(A,B)+\operatorname{dist}(B,C)\)
由于 \(\operatorname{dist}(A,C)\) 需要满足其操作数最小,因此对于任意一种合法的 \(A\gets C\) 操作方案,\(\operatorname{dist}(A,C)\) 应该不大于其操作数,而 \(A\gets B\gets C\) 的方案显然也是一种 \(A\gets C\) 的合法操作方案,所以得到 \(\operatorname{dist}(A,C)\le\operatorname{dist}(A,B)+\operatorname{dist}(B,C)\)
注意到如下的观察:
观察二:
对于 \(S\) 的最后一个字符 \(c\),设 \(c\) 在 \(T\) 中最后一次出现是在位置 \(x\) 上,那么 \(\operatorname{dist}(S,T)=(n-x)+\operatorname{dist}(S-S_n,T-T_x)\)
考虑在计算两个排列的距离的方法,每次复原最后一个字符,然后解决前面长度 \(n-1\) 的子串
对于此处,我们也可以从后到前依次复位,不过每次把哪个 \(c\) 放到 \(T_n\) 上是我们需要解决的问题
考虑贪心,每次选取最后的一个 \(c\) 放到 \(T_n\) 上,此时代价为 \((n-x)\),而剩下的字符串复位的代价就是 \(\operatorname{dist}(S-S_n,T-T_x)\)
现在我们要证明这个贪心的正确性,那么不妨考虑一个下标 \(x_1\) 满足 \(x_1<x\) 且 \(T_{x_1}=c\)
那么我们只需证明 \((n-x)+\operatorname{dist}(S-S_n,T-T_x)\le(n-x_1)+\operatorname{dist}(S-S_n,T-T_{x_1})\),事实上这等价于证明 \(\operatorname{dist}(S-S_n,T-T_x)\le (x-x_1)+\operatorname{dist}(S-S_n,T-T_{x_1})\)
而我们又注意到 \(x-x_1=\operatorname{dist}(T-T_x,T-T_{x_1})\),因此根据观察一,原命题得证
为了维护 \(\operatorname{dist}(S,T)\),我们对每个位置 \(i\) 维护 \(T_i\) 是否已经匹配,然后倒序考虑每个 \(x\),\(x\) 移动到匹配位置的代价事实上就等于 \((x,n]\) 中未匹配的位置数量,显然这个用一棵树状数组可以在 \(\Theta(n\log n)\) 的时间内解决
事实上,考察上面计算 \(\operatorname{dist}(S,T)\) 的过程,假如我们记录下每个 \(x\) 何时候被匹配,记为 \(c_i\),事实上 \(\operatorname{dist}(S,T)\) 与序列 \(\{c_i\}\) 的逆序对数是相等的
不过在这题中,\(T\) 的可能性太多了,逐一验证的复杂度显然会超时,考虑剪枝
而我们注意到如下的观察:
观察三:
最大化 \(\operatorname{dist}(S,T)\) 的 \(T\) 中相同的字符一定连续
考虑任意一个 \(T\),计算 \(\{c_i\}\),考虑两个字符相同的位置 \(T_i\) 和 \(T_j\),为了简化讨论,我们假设 \(i<j\) 且 \(T_{i+1}\sim T_{j-1}\) 中没有与 \(T_i,T_j\) 相等的字符,显然根据 \(\{c_i\}\) 的定义有 \(c_i<c_j\)
此时我们只需要证明总存在一种方式使 \(T_i,T_j\) 相邻且不减少 \(\{c_i\}\) 的逆序对数
由于要让这两个相邻,一种显然的方法就是循环移位,而根据移动的字符分成如下两种情况:
- 让 \(T_{i+1}\sim T_{j-1}\) 的字符全部向后移动 \(1\) 位,并把 \(T_j\) 移动到 \(T_{i+1}\) 上
- 让 \(T_{i+1}\sim T_{j-1}\) 的字符全部向前移动 \(1\) 位,并把 \(T_i\) 移动到 \(T_{j-1}\) 上
考虑区间 \((i,j)\) 中的每一个 \(k\),考虑修改后 \(k\) 对答案的贡献
- 对于第一种方式,若 \(c_k<c_j\),那么逆序对数 \(+1\),如果 \(c_j<c_k\),那么逆序对数 \(-1\)
- 对于第二种方式,若 \(c_i<c_k\),那么逆序对数 \(-1\),如果 \(c_k<c_i\),那么逆序对数 \(+1\)
记 \(\operatorname{cnt^\uparrow}(x)\) 表示 \(c_{i+1}\sim c_{j-1}\) 中 \(>x\) 的数的个数,而 \(\operatorname{cnt^\downarrow}(x)\) 表示 \(c_{i+1}\sim c_{j-1}\) 中 \(<x\) 的数的个数
根据上面的分析,我们得到第一种方式对逆序对数的贡献为 \(\operatorname{cnt^\downarrow}(c_j)-\operatorname{cnt^\uparrow}(c_j)\),第二种方式对逆序对数的贡献为 \(\operatorname{cnt^\uparrow}(c_i)-\operatorname{cnt^\downarrow}(c_i)\)
假如 \(\operatorname{cnt^\downarrow}(c_j)-\operatorname{cnt^\uparrow}(c_j)\ge0\),那么直接选择第一种操作就可以使得 \(T_i,T_j\) 相邻且 \(\{c_i\}\) 逆序对数量不减
假如 \(\operatorname{cnt^\downarrow}(c_j)-\operatorname{cnt^\uparrow}(c_j)<0\),即 \(\operatorname{cnt^\downarrow}(c_j)<\operatorname{cnt^\uparrow}(c_j)\)
由于 \(c_i<c_j\),我们知道 \(\operatorname{cnt^\uparrow}(c_i)\ge \operatorname{cnt^\uparrow}(c_j),\operatorname{cnt^\downarrow}(c_i)\le\operatorname{cnt^\downarrow}(c_j)\),与 \(\operatorname{cnt^\downarrow}(c_j)<\operatorname{cnt^\uparrow}(c_j)\) 联立得到:\(\operatorname{cnt^\downarrow}(c_i)\le\operatorname{cnt^\downarrow}(c_j)<\operatorname{cnt^\uparrow}(c_j)\le\operatorname{cnt^\uparrow}(c_i)\)
因此此时 \(\operatorname{cnt^\uparrow}(c_i)>\operatorname{cnt^\downarrow}(c_i)\),所以第二种操作的代价 \(\operatorname{cnt^\uparrow}(c_i)-\operatorname{cnt^\downarrow}(c_i)>0\) ,此时选择第二种操作可以使得 \(T_i,T_j\) 相邻且 \(\{c_i\}\) 逆序对数量不减
根据上面的分析,我们知道对于任何一对字符相同的 \(T_i,T_j\),若 \(T_{i+1}\sim T_{j-1}\) 中没有与其相同的字符,总存在一种方式使得 \(T_i,T_j\) 相邻并且 \(\operatorname{dist}(S,T)\) 不减少
根据上面的观察,我们只需要枚举 \(\texttt{a},\texttt{t},\texttt{o},\texttt{n}\) 的先后顺序即可
时间复杂度 \(\Theta(\alpha(S)!\times n\log n)\),其中 \(\alpha(S)\) 表示 \(S\) 的字符集大小(\(\alpha(S)\le 4\))
代码呈现
#include<bits/stdc++.h>
#define int long long
#define pci pair<char,int>
using namespace std;
const int MAXN=1e5+1;
struct BitTree {
int len,tree[MAXN];
inline int lowbit(int x) { return x&-x; }
inline void Modify(int x,int v) {
for(;x<=len;x+=lowbit(x)) tree[x]+=v;
}
inline int Query(int x) {
int ret=0;
for(;x;x-=lowbit(x)) ret+=tree[x];
return ret;
}
} B;
inline int dist(string ori,string tar) {
int n=tar.size(),ans=0;
B.len=n;
ori="#"+ori,tar="#"+tar;
map <char,vector <int> > lst;
for(int i=1;i<=n;++i) lst[ori[i]].push_back(i);
for(int i=1;i<=n;++i) B.Modify(i,1);
for(int i=n;i>=1;--i) {
int x=lst[tar[i]].back();
ans+=B.Query(n)-B.Query(x);
B.Modify(x,-1),lst[tar[i]].pop_back();
}
return ans;
}
inline void solve() {
string str,res;
int ans=0;
cin>>str;
map <char,int> cnt;
int n=str.length();
for(int i=0;i<n;++i) ++cnt[str[i]];
vector <int> p; vector <pci> sec;
for(int i=0;i<(int)cnt.size();++i) p.push_back(i);
for(auto x:cnt) sec.push_back(x);
do {
string tmp;
for(int i:p) {
for(int j=1;j<=sec[i].second;++j) {
tmp.push_back(sec[i].first);
}
}
int val=dist(tmp,str);
if(val>=ans) ans=val,res=tmp;
} while(next_permutation(p.begin(),p.end()));
cout<<res<<endl;
}
signed main() {
int T;
cin>>T;
while(T--) solve();
return 0;
}
VI. [LOJ6038] - 远行
思路分析
注意到每一个连通块都一定是一棵树,根据直径的性质,从树上某点出发的最长路一定是到直径的某个端点
因此我们只需要维护每棵树的直径和直径到树上节点的距离
先考虑如何在加边之后维护树的直径,显然新的直径的端点一定是原来的两棵树的四个直径端点中的某两个,因此树的直径的维护也转化为求树上距离的问题
求树上距离,想到用倍增暴力维护 LCA 和深度,但是每次连边的时候要扫一遍整棵树重构倍增,复杂度是 \(\Theta(qn\log n)\) 的,显然会超时
注意到如果我们把一棵大小 \(x\) 的树重构并到另一棵树上,复杂度是 \(\Theta(x\log n)\) 的,与另一棵树的大小无关,因此考虑启发式合并,每次对于大小较小的一棵树重构其父亲和深度,而对于大小较大的树保持不变,此时每个节点重构时其所在的树的大小至少扩大一倍,因此每个点至多被重构 \(\Theta(\log n)\) 次
所以我们证明了启发式合并的复杂度是 \(\Theta(n\log^2n)\) 的
本题总体时间复杂度:\(\Theta(q\log n+n\log^2 n)\) 可以通过(听说正解是 LCT 维护直径但我不会)
代码呈现
#include<bits/stdc++.h>
using namespace std;
const int MAXN=3e5+1;
vector <int> G[MAXN];
int dsu[MAXN],siz[MAXN],dep[MAXN],fa[MAXN][20];
inline int find(int x) {
if(dsu[x]==x) return x;
return dsu[x]=find(dsu[x]);
}
inline void dfs(int p,int f) {
fa[p][0]=f;
dep[p]=dep[fa[p][0]]+1;
for(int k=1;k<20;++k) fa[p][k]=fa[fa[p][k-1]][k-1];
for(int v:G[p]) if(v!=f) dfs(v,p);
}
int dia[MAXN][2];
inline int LCA(int x,int y) {
if(dep[x]<dep[y]) swap(x,y);
for(int k=19;k>=0;--k) if(dep[fa[x][k]]>=dep[y]) x=fa[x][k];
if(x==y) return x;
for(int k=19;k>=0;--k) if(fa[x][k]!=fa[y][k]) x=fa[x][k],y=fa[y][k];
return fa[x][0];
}
inline int dis(int x,int y) {
return dep[x]+dep[y]-2*dep[LCA(x,y)];
}
signed main() {
int type,n,q,lst=0;
scanf("%d%d%d",&type,&n,&q);
for(int i=1;i<=n;++i) dsu[i]=i,dep[i]=1,siz[i]=1,dia[i][0]=dia[i][1]=i;
while(q--) {
int op;
scanf("%d",&op);
if(op==1) {
int x,y;
scanf("%d%d",&x,&y);
if(type) x^=lst,y^=lst;
int u=find(x),v=find(y);
if(siz[u]<siz[v]) swap(u,v),swap(x,y);
dsu[v]=u,siz[u]+=siz[v];
G[x].push_back(y),G[y].push_back(x);
dfs(y,x);
int len=0;
for(int s:{dia[u][0],dia[u][1],dia[v][0],dia[v][1]}) {
for(int t:{dia[u][0],dia[u][1],dia[v][0],dia[v][1]}) {
len=max(len,dis(s,t));
}
}
for(int s:{dia[u][0],dia[u][1],dia[v][0],dia[v][1]}) {
for(int t:{dia[u][0],dia[u][1],dia[v][0],dia[v][1]}) {
if(dis(s,t)==len) {
dia[u][0]=s,dia[u][1]=t;
goto upd;
}
}
}
upd:;
}
if(op==2) {
int x;
scanf("%d",&x);
if(type==1) x^=lst;
int u=find(x);
lst=max(dis(x,dia[u][0]),dis(x,dia[u][1]));
printf("%d\n",lst);
}
}
return 0;
}
VII. [CF111D] - Petya and Coloring
思路分析
设 \(\mathbf S_i\) 表示第 \(i\) 列使用的颜色集合,\(\mathbf L_i\) 表示第 \(1\) 列到第 \(i\) 列用的颜色集合,\(\mathbf R_i\) 表示第 \(i\) 列到第 \(n\) 列用的颜色集合
考虑从 \(\mathbf L_i\) 转移到 \(\mathbf L_{i+1}\) 的过程,由定义我们知道 \(\mathbf L_{i+1}=\mathbf L_{i}\cup\mathbf S_{i+1}\),所以我们可以得到 \(\mathbf L_i\subseteq \mathbf L_{i+1}\),因此得到 \(|\mathbf L_i|\le |\mathbf L_{i+1}|\),因此,\(|\mathbf L_{1}|\sim|\mathbf L_m|\) 单调不降
同理,我们可以得到 \(|\mathbf R_1|\sim|\mathbf R_m|\) 单调不升
但是,我们有 \(|\mathbf L_1|=|\mathbf R_2|,|\mathbf L_2|=|\mathbf R_3|,\cdots,|\mathbf L_{m-1}|=|\mathbf R_m|\)
所以 \(|\mathbf R_2|=|\mathbf L_1|\leq |\mathbf L_2|=|\mathbf R_{3}|\),又 \(|\mathbf R_3|\le|\mathbf R_2|\),所以得到 \(|\mathbf R_2|=|\mathbf R_3|\)
类推可知,\(|\mathbf L_1|=|\mathbf L_2|=\cdots=|\mathbf L_{m-1}|=|\mathbf R_2|=|\mathbf R_3|=\cdots=|\mathbf R_m|\)
考虑 \(\mathbf S_1\) 和 \(\mathbf S_2\) 的关系,由定义可得 \(\mathbf S_1=\mathbf L_1,\mathbf S_1\cup\mathbf S_2=\mathbf L_2\),所以有 \(\mathbf L_1\subseteq\mathbf L_{2}\),又因为 \(|\mathbf L_1|=|\mathbf L_2|\),所以我们得到:\(\mathbf L_1=\mathbf L_2\)
所以有 \(\mathbf S_1=\mathbf S_1\cup\mathbf S_2\) 因此 \(\mathbf S_2\subseteq \mathbf S_1\)
同理继续分析,考虑 \(\mathbf L_2\) 和 \(\mathbf L_3\) 的关系,注意到 \(\mathbf L_2=\mathbf L_1=\mathbf S_1\),所以类似上面的过程,也能得到 \(\mathbf S_3\subseteq\mathbf S_1\)
类推到 \(\mathbf S_4\sim\mathbf S_{m-1}\),都有这个性质,最终我们得到 \(\mathbf S_2\sim\mathbf S_{m-1}\subseteq \mathbf S_1\)
然后再看 \(\mathbf R _m\) 和 \(\mathbf R_{m-1}\) 的关系,观察到 \(\mathbf R_m=\mathbf S_m\),然后用上面类似的方法同理可得:\(\mathbf S_{2}\sim\mathbf S_{m-1}\subseteq \mathbf S_{m}\)
联立上下,可知 \(\mathbf S_2\sim\mathbf S_{m-1}\subseteq \mathbf S_1\cap\mathbf S_m\)
又因为 \(|\mathbf L_1|=|\mathbf R_m|\) 且 \(\mathbf L_1=\mathbf S_1,\mathbf R_m=\mathbf S_m\),所以有 \(|\mathbf S_1|=|\mathbf S_m|\)
此时整理一下我们的得到的条件:
- \(|\mathbf S_1|=|\mathbf S_m|\)
- \(\forall i\in(1,m),\mathbf S_i\in \mathbf S_1\cap\mathbf S_m\)
然后我们可以考虑进行计数,首先枚举 \(|\mathbf S_1|,|\mathbf S_m|\),设为 \(p\),然后枚举 \(|\mathbf S_1\cap\mathbf S_m|\),设为 \(i\),然后考虑分步计数:
-
确定 \(\mathbf S_1,\mathbf S_m\),首先求出 \(\mathbf S_1\cap\mathbf S_m\),共有 \(\dbinom ki\) 种情况,然后求出 \(\mathbf S_1\) 的剩下部分,共有 \(\dbinom{k-i}{p-i}\) 种情况,最后求出 \(\mathbf S_m\) 的剩下部分,共有 \(\dbinom {k-p}{p-i}\) 种情况,总数即三步情况数相乘,共有 \(\dbinom ki\dbinom{k-i}{p-i}\dbinom{k-p}{p-i}\) 种
-
求出中间 \(m-2\) 列的具体涂色情况,每个格子都有 \(i\) 种涂色方式,没有其它的限制,故情况数为 \(i^{n(m-2)}\)
-
求出第 \(1\) 列和第 \(m\) 列的染色情况,不难发现这两列的染色情况数是相同的,且只与 \(p\) 有关,即恰好使用 \(p\) 种颜色染 \(n\) 个格子的方案数,不妨记为 \(f_n(p)\),显然,我们可以通过容斥原理计算 \(f_n(p)\) 的值,考虑枚举强制让 \(x\) 个格子不选,其余列无限制的方案数,显然就是 \((n-x)^p\) 种,然后做一次简单容斥可得:
综上所述,我们得到:
\[\text{Answer}=\sum_{p=1}^{\min(k,n)}\left[\sum_{x=0}^n (-1)^x\dbinom px(n-x)^p\right]^2\left[\sum_{i=0}^p \dbinom ki\dbinom{k-i}{p-i}\dbinom{k-p}{p-i}i^{n(m-2)}\right] \]直接计算,时间复杂度 \(\Theta(n^2)\)
代码呈现
#include<bits/stdc++.h>
using namespace std;
#define int long long
const int MAXN=1e6+1,MOD=1e9+7;
int inv[MAXN],fac[MAXN];
inline int ksm(int a,int b=MOD-2,int m=MOD) {
int res=1;
while(b) {
if(b&1) res=res*a%m;
a=a*a%m;
b=b>>1;
}
return res;
}
inline void init() {
fac[0]=inv[0]=1;
for(int i=1;i<MAXN;++i) fac[i]=fac[i-1]*i%MOD;
inv[MAXN-1]=ksm(fac[MAXN-1]);
for(int i=MAXN-2;i>0;--i) inv[i]=inv[i+1]*(i+1)%MOD;
}
inline int C(int m,int n) {
if(n<0||n>m) return 0;
return fac[m]*inv[n]%MOD*inv[m-n]%MOD;
}
signed main() {
init();
int n,m,k,res=0;
scanf("%lld%lld%lld",&n,&m,&k);
if(m==1) {
printf("%lld\n",ksm(k,n));
return 0;
}
for(int p=1;p<=k&&p<=n;++p) {
int f=0;
for(int i=0,op=1;i<=p;++i,op*=-1) {
f+=op*C(p,i)*ksm(p-i,n)%MOD;
f=(f%MOD+MOD)%MOD;
}
for(int i=0;i<=p;++i) {
int t=f*f%MOD;
t=t*C(k,i)%MOD;
t=t*C(k-i,p-i)%MOD;
t=t*C(k-p,p-i)%MOD;
t=t*ksm(i,n*(m-2))%MOD;
res=(res+t)%MOD;
}
}
printf("%lld\n",res);
return 0;
}
VIII. 简单快速幂
题目大意
给定一个质数 \(p\),请求出:对于均匀随机正整数变量 \(m,n\),\(m^n\bmod p=1\) 的概率
共 \(T\) 次询问,保证 \(T\le 10^6,p\le10^9\)
思路分析
首先,由费马小定理和余数的基本性质可得:
\[\begin{aligned} &\because \begin{cases} m^{p-1}\equiv 0\pmod p\\ p^n\equiv0\pmod p \end{cases}\\ &\therefore \begin{cases} m^n\equiv m^{n\bmod(p-1)}\pmod p\\ m^n\equiv(m\bmod p)^n\pmod p \end{cases}\\ &\therefore m^n\equiv (m\bmod p)^{n\bmod(p-1)}\pmod p \end{aligned} \]所以我们只需要考虑 \(1\le m\le p,1\le n\le p-1\) 的情况,记答案为 \(P\),则有:
\[P=\dfrac{\sum_{m=1}^p\sum_{n=1}^{p-1} [m^n\bmod p=1]}{p(p-1)} \]考虑优化掉第二重求和号,解决如下问题:
给定正整数 \(m\),质数 \(p\),求:对于 \(1\sim p-1\) 的整数 \(n\),有多少个 \(n\) 满足 \(m^n\bmod p=1\)
考虑从阶的定义出发,因为题目中所要满足的条件等价于 \(\delta_p(m)\mid n\),其中 \(\delta_p(m)\) 为 \(m\) 模 \(p\) 的阶
所以满足条件的 \(n\) 的个数为 \(\left[\dfrac{p-1}{\delta_p(m)}\right]\)
注意到 \(m^{p-1}\bmod p=1\),所以 \(\delta_p(m)\mid p-1\),所以可以拆掉高斯记号,所求即为 \(\dfrac{p-1}{\delta_p(m)}\)
注意到 \(m=p\) 时无满足情况,所以原式被化简成:
\[P=\dfrac{\sum_{m=1}^{p-1} \dfrac{p-1}{\delta_p(m)}}{p(p-1)} \]然后考虑优化 \(\delta(m)\) 的计算,可以联想一下原根的知识,如果我们设 \(r\) 为模 \(p\) 的原根,即 \(\delta_p(r)=p-1\)
由阶的性质不难推知 \(r^1\bmod p\sim r^{p-1}\bmod p\) 互不相同,且 \(r^1\bmod p\sim r^{p-1}\bmod p\) 与 \(1\sim p-1\) 是一一对应的关系
不妨设 \(\lambda_p(m)\) 为满足 \(r^n\bmod p=m\) 且 \(n\in [1,p-1]\) 的正整数 \(n\),则对于任意 \(m\in[1,p-1]\),\(\lambda_p(m)\) 是唯一的
此时将 \(r^{\lambda_p(m)}\bmod p=m\) 带入 \(\delta_p(m)\) 的定义中,进行变形可得:
\[\begin{aligned} m^{\delta_p(m)}&\equiv 1 \pmod p\\ (r^{\lambda_p(m)})^{\delta_p(m)}&\equiv 1 \pmod p\\ r^{\lambda_p(m)\delta_p(m)}&\equiv 1 \pmod p \end{aligned} \]又因 \(\delta_p(r)=p-1\),所以 \(p-1\mid\lambda_p(m)\delta_p(m)\)
不难推知 \(p-1\mid \gcd(\lambda_p(m),p-1)\gcd(\delta_p(m),p-1)\),若符合阶的定义,则需使 \(\delta_p(m)\) 尽可能小,易得:此时 \(\delta_p(m)=\dfrac{p-1}{\gcd(\lambda_p(m),p-1)}\)
将上式带入 \(P\) 的计算中可得:
\[\begin{aligned} P&=\dfrac{\sum_{m=1}^{p-1} \dfrac{p-1}{\delta_p(m)}}{p(p-1)}\\ P&=\dfrac{\sum_{m=1}^{p-1} (p-1)\div{\dfrac{p-1}{\gcd(\lambda_p(m),p-1)}}}{p(p-1)}\\ P&=\dfrac{\sum_{m=1}^{p-1} \gcd(\lambda_p(m),p-1)}{p(p-1)} \end{aligned} \]注意到 \(\lambda_p(1)\sim\lambda_p(p-1)\) 恰好一一对应 \(1\sim p-1\) 之间的每一个正整数,所以可以继续化简:
\[P=\dfrac{\sum_{m=1}^{p-1}\gcd(p-1,m)}{p-1} \]考虑继续化简分子,记 \(S(n)=\sum_{m=1}^{n}\gcd(n,m)\),原式可以继续化简:
\[P=\dfrac{S(p-1)}{p(p-1)} \]对于 \(S(n)\) 进行化简,由 \(\gcd\) 的性质得到:
改变枚举顺序:枚举 \(k\) 的每一个因数 \(d\),统计 \(d\) 作为 \(\gcd\) 时的方法数
设此时 \(m=kd\),满足 \(k\le \dfrac{n}{d},\gcd(k,\dfrac{n}{d})=1\),从 \(\varphi(n)\) 的定义出发,发现此时方案数恰等于 \(\varphi(\dfrac{n}{d})\),带入进 \(S(n)\) 表达式并化简有:
\[\begin{aligned} S(n)&=\sum_{m=1}^n\gcd(n,m)\\ &=\sum_{d\mid n} d\times\varphi(\dfrac{n}{d}) \end{aligned} \]设 \(n=\prod p_i^{a_i}\) 对 \(d\) 进行质因数分解,设 \(d=\prod p_i^{a'_i}\) 可以进一步改写成如下的形式:
\[\begin{aligned} S(n) &=\sum_{d\mid n} \prod p_i^{a'_i}\times \varphi(p_i^{a_i-a'_i})\\ &=\prod_{i}\sum_{a'_i=0}^{a_i} p_i^{a'_i}\times\varphi(p_i^{a_i-a'_i})\\ &=\prod_{i}p_i^{a_i}+\sum_{a'_i=0}^{a_i-1} p_i^{a'_i}\times (p_i^{a_i-a'_i}-p_i^{a_i-a'_i-1})\\ &=\prod_i (a_i+1)\times p_i^{a_i}-a_i\times p_{i}^{a_i-1} \end{aligned} \]因此进行一次质因数分解即可快速计算 \(S(n)\) 的值
时间复杂度 \(\Theta(\sqrt p+T\dfrac{\sqrt p}{\ln p})\)
标签:cnt,mathbf,int,选讲,MAXN,题目,operatorname,dist From: https://www.cnblogs.com/DaiRuiChen007/p/17055128.html