21 图像旋转
opencv知识点:
- 仿射变换 -
warpAffine - 计算二维旋转的仿射矩阵 -
getRotationMatrix2D
本课所解决的问题:
- 如何理解图像几何变换和图像变换?
- 图像几何变换都有什么变换?
- 如何理解仿射变换和透视变换?
- 如何实现图像的旋转?
提示在前:
笔者为了理解图像旋转的warpAffine,引申了很多其他的概念
1.图像几何变换和图像变换
为了更好的理解图像翻转,图像旋转等,我们首先介绍一下变换相关的概念
图像的变换,从严格意义上来说分为两种
- 几何变换
- 图像变换
简述
图像几何变换:
改变图像的大小或形状。
比如图像的平移、旋转、放大、缩小等,这些方法在图像配准中使用较多。
图像变换:
通过数学映射的方法,将空域的图像信息转换到频域、时频域等空间上进行分析。
比如傅里叶变换、小波变换等。
区别
文章引用:简述图像几何变换和图像变换的区别
图像几何变换和图像变换的区别为:性质不同,包括不同,原始图像不同。
(1)性质
图像几何变换是从具有几何结构之集合至其自身或其他此类集合的一种对射。
图像变换将原定义在图像空间的图像以某种形式转换到另外的空间,利用空间的特有性质方便地进行一定的加工,最后再转换回图像空间以得到所需的效果。
(2)包括
图像几何变换包括翻折变换、平移变换、旋转变换等。
图像变换包括傅里叶变换、沃尔什-阿达玛变换等。
(3)原始图像
- 图像几何变换的原始图像为平面域图像。
- 图像变换的原始图像为空间域图像
2.图像几何变换
而图像的几何变换,又可以分为三类:
- 刚性变换
- 仿射变换
- 透视变换
三类变换
刚性变换:
只有物体的位置(平移变换)和朝向(旋转变换)发生改变,而形状不变,得到的变换称为刚性变换。
仿射变换:
仿射变换是从一个二维坐标系变换到另一个二维坐标系,属于线性变换。
通过已知3对坐标点可以求得变换矩阵。
透视变换:
透视变换是从一个二维坐标系变换到一个三维坐标系,属于非线性变换。
通过已知4对坐标点可以求得变换矩阵。
基本变换、仿射变换和透视变换
图像的几何变换包含很多变换,其中有一些基本变换,具体如下
- 平移(Translation)
- 缩放(Scale)
- 旋转(Rotation)
- 翻转(Flip)
- 错切(Shear)
而仿射变换和透视变换就是对这些基本变换进行组合实现的
也就是说,仿射变换和透视变换包含所有的基本变换,同时也作为基本变换的某种组合
在opencv中,针对它们已经封装好了对应的API,分别为
仿射变换 - warpAffine
透视变换 - warpPerspective
3.图像旋转
说回图像旋转
从上文我们知道了一些关键点
- 图像旋转就是图像几何变换中,基本变换的一种
- 仿射变换和透视变换包含所有的基本变换
所以我们可以通过仿射变换
API——warpAffine实现图像旋转
在opencv中,如果我们想对一个图像进行旋转,要用到两个API
- warpAffine
- getRotationMatrix2D
这里分别对它们进行解释
warpAffine
warpAffine
仿射变换
共7个参数
第1个参数 输入
第2个参数 输出
第3个参数 输入的变换矩阵(2行3列)
第4个参数 输出图像的size
第5个参数 插值方法
第6个参数 边界模式(暂且不学习。深入探讨的话,还会涉及很多的东西)
第7个参数 边界颜色(暂且不学习。深入探讨的话,还会涉及很多的东西)
getRotationMatrix2D
getRotationMatrix2D
计算二维旋转的仿射矩阵
共3个参数
第1个参数 图像的旋转中心
第2个参数 旋转角度
(规定坐标原点左上角,正值表示逆时针旋转)
第3个参数 各向同性比例因子(对图像本身大小的放缩)
变换矩阵
介绍完毕后,我们知道图像旋转的关键就是那个变换矩阵
变换矩阵可以由getRotationMatrix2D得到
现在我们来研究一下得到的变换矩阵
由于本变换矩阵是由
getRotationMatrix2D得到,是专门对标仿射变换API的
在opencv中规定其为2行3列的矩阵。

当旋转的角度为Θ,且旋转中心为x,y时,即这个矩阵的通式为
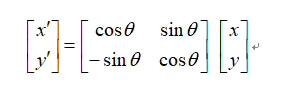
当旋转中心为左上角时,这时候的变换矩阵为
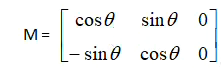
像素点位置
最后当我们调用warpAffinie时,经过如下公式的计算,就能得到变换后的像素点位置
我们就能实现图像旋转
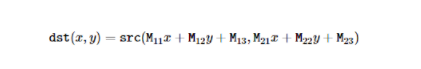
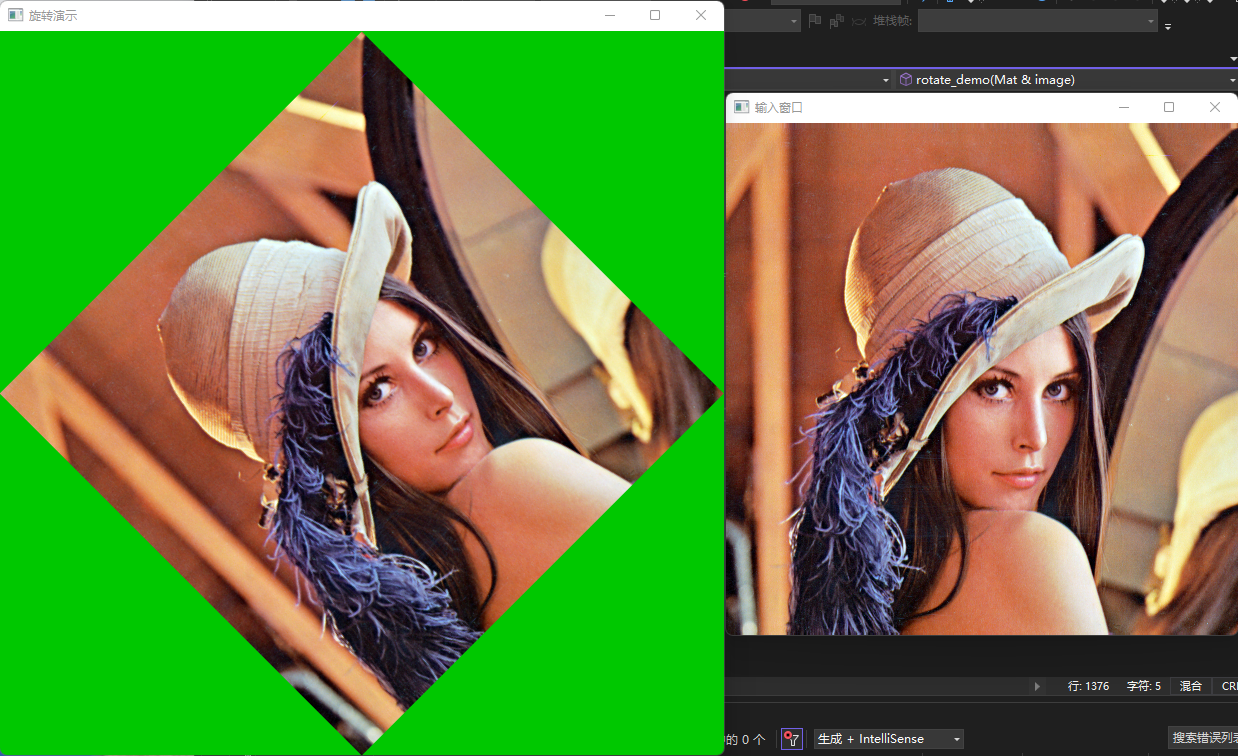
4.对一张图像进行旋转
接下来,我们进行对一张图像进行旋转的演示
第一版 - 原图像大小
//函数定义
void rotate_demo(Mat& image);
//函数实现
void QuickDemo::rotate_demo(Mat& image) {
Mat dst, M;//M为变换矩阵
int w = image.cols;
int h = image.rows;
M = getRotationMatrix2D(Point2f(w / 2, h / 2), 45, 1.0);
warpAffine(image, dst, M, image.size(), INTER_LINEAR, 0, Scalar(0, 200, 0));
imshow("旋转演示", dst);
}
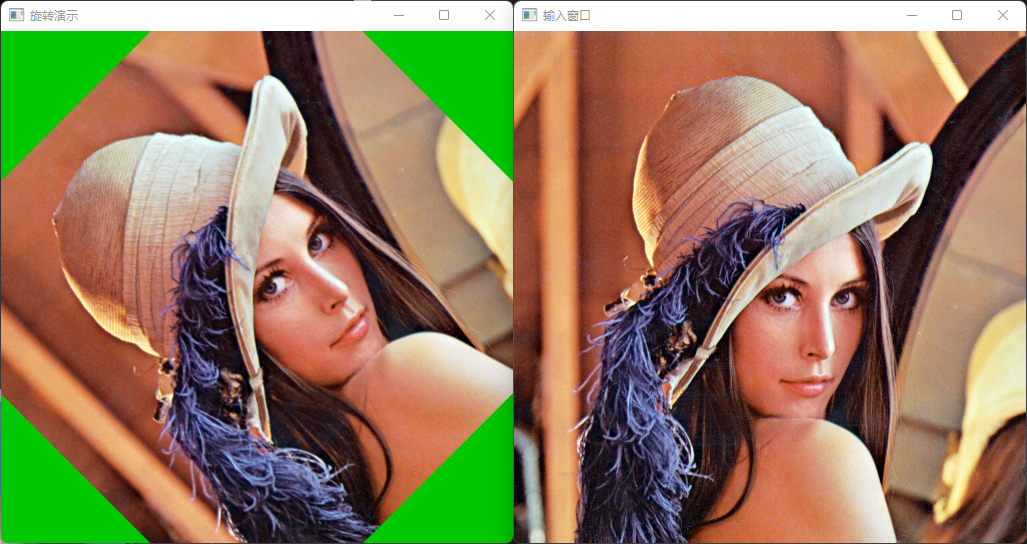
第二版 - 新图像大小
第一版中,旋转后的图像并没有完全显示出来,而是为原图像的大小
如果我们想让图像全部显示出来,该怎么处理呢?
处理方法如下:
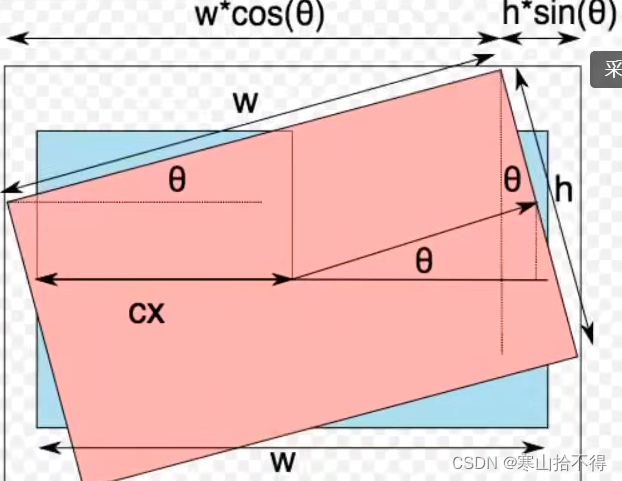
通过如上图,我们可以计算新图像的宽度,高度,旋转中心的通式
- 新宽度
nw = w*cosΘ + h*sinΘ- 新宽度
nh = w*sinΘ + h*cosΘ- 新旋转中心
x +=( nw/2 - w/2)- 新旋转中心
y +=( nh/2 - h/2)
void QuickDemo::rotate_demo(Mat& image) {
Mat dst, M;//M为变换矩阵
int w = image.cols;
int h = image.rows;
M = getRotationMatrix2D(Point2f(w / 2, h / 2), 45, 1.0);
//C++的abs则可以自然支持对整数和浮点数两个版本(实际上还能够支持复数)
double cos = abs(M.at<double>(0, 0));
double sin = abs(M.at<double>(0, 1));
int nw = w * cos + h * sin;
int nh = w * sin + h * cos;
//新图像的旋转中心
M.at<double>(0, 2) += (nw / 2 - w / 2);
M.at<double>(1, 2) += (nh / 2 - h / 2);
warpAffine(image, dst, M, Size(nw,nh),INTER_LINEAR,0,Scalar(0,200,0));
imshow("旋转演示", dst);
}