SLAM学习笔记—后端
-
概述
-
状态估计概率分布的核心思想
未知量(\(x_k\))的后验概率分布 = 似然概率分布 × 未知量(\(x_k\))的先验概率分布
这一等式贯穿全文,请牢牢抓住!
-
运动方程和观测方程
\[\begin{cases} x_k = f(x_{k-1},u_k)+w_k \\\\ z_k=h(x_k)+v_k \end{cases} ,k=1,2,\cdots,N \]
其中\(x_k\overset{def}{=}\{x_k,y_1\cdots,y_m\}\),表示\(k\)时刻所有的未知量(观测位姿,路标位置)
- 运动方程用来估计未知量的先验(预测):先估计出一个先验\(\hat{x}_k\);
- 观测方程用来估计未知量的后验(更新):观测先验值后消除其不确定性,得出确切数值\(x_k\),然后利用似然概率估计观测值\(z_k\),最后利用\(z_k\)校正\(x_k\)得到后者的后验分布\(\check{x}_k\);
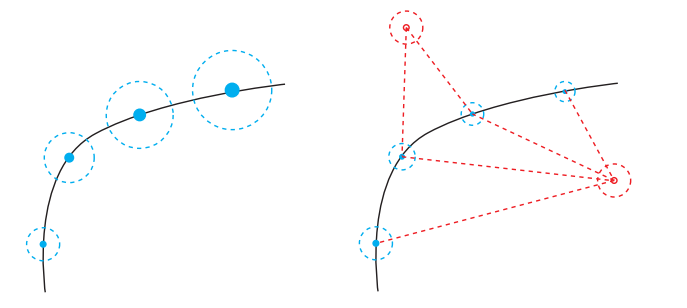
可以看到左图,如果对未知量\(x_k\)做先验估计,由于误差的积累,系统噪音会越来越大。
但是如果通过观测路标点来矫正未知量,对其做后验估计,则误差不会一直增加。
-
线性系统和KF
就是运动方程和观测方程均可以线性表出。
-
-
状态估计概率分布(贝叶斯法则在运动方程和观测方程中的应用)
- \(k\)时刻未知量的后验概率分布记为\(P(\check{x}_k)\),其实际含义为:在已知\(x_0,u_{1:k},z_{1:k}\)的情况下,\(x_k\)的后验概率分布。所以也可以记为\(P(x_k|x_0,u_{1:k},z_{1:k})\);
- \(k\)时刻未知量的先验概率分布记为\(P(\hat{x}_k)\),其实际含义为:在未知\(z_k\)(也就是只已知\(x_0,u_{1:k},z_{1:k-1}\))的情况下,\(x_k\)的先验概率分布。所以也可以记为\(P(x_k|x_0,u_{1:k},z_{1:k-1})\);
- \(k\)时刻的似然概率分布记为\(P(z_k)\),其实际含义为:在已知未知量的先验值的基础上,观测值\(z_k\)的概率分布。所以也可以记为\(P(z_k|x_k)\);
所以,利用贝叶斯法则有:\(P(x_k|x_0,u_{1:k},z_{1:k})\varpropto P(z_k|x_k)·P(x_k|x_0,u_{1:k},z_{1:k-1})\);
-
线性系统和\(\mbox{KF(Kalman Filter)}\)【非主流】
根据条件概率的公式\(P(A|B)\cdot P(B)=P(B|A)\cdot P(A)\)可得:
\[P(x_k|x_o,u_{1:k},z_{1:k})\cdot P(x_0,u_{1:k},z_{1:k}) =P(x_o,u_{1:k},z_{1:k}|x_k)\cdot P(x_k) \]从而引入全概率公式\(P(A_i|B)=\frac{P(B|A_i)\cdot P(A_i)}{\sum P(B)\cdot P(B|A_j)}\propto P(B|A_i)\cdot P(A_i)\)可得:
\[P(x_k|x_o,u_{1:k},z_{1:k}) \propto P(x_o,u_{1:k},z_{1:k}|x_k)\cdot P(x_k) \]通过观察其中的物理含义,也就是“后验=似然×先验”:
-
\(P(x_k|x_o,u_{1:k},z_{1:k})\)代表在修正后得出的位姿分布,也就是后验概率;
-
\(P(x_o,u_{1:k},z_{1:k}|x_k)\)代表在已知分布后如何修正它的最佳分布,也就是似然概率。显然\(k\)时刻的位姿不能影响过去任何一刻的位姿,所以可以简化为\(P(z_k|x_k)\);
-
\(P(x_k)\)代表\(k\)时刻的位姿,本质上就是已知\(1:k-1\)时刻的修正位姿和\(1:k\)时刻的修正输入,得到的当前时刻的位姿分布,所以完整表述应该是\(P(x_k|x_0,u_{1:k},z_{1:k-1})\);
最后为了区分先验概率和后验概率,我们记先验分布为\(\hat{x}_k\)、后验概率为\(\check{x}_k\):
\[P(\check{x}_k|x_o,u_{1:k},z_{1:k})\propto P(z_k|\hat{x}_k)\cdot P(\hat{x}_k|x_0,u_{1:k},z_{1:k-1}) \]我们假设当前状态\(x_k\)只与其前一刻的状态相关,也就是说我们将先验概率分布函数按照\(x_{k-1}\)全概展开:
\[\begin{aligned} P(B|C)&=\sum_{i=1}^{N}P(B|A_iC)·P(A_iC),其中B为\hat{x}_k,A为\check{x}_{k-1} \\ P(\hat{x}_k|x_0,u_{1:k},z_{1:k-1})&=\int P(\hat{x}_k|\check{x}_{k-1},x_0,u_{1:k},z_{1:k-1})·P(\check{x}_{k-1}|x_0,u_{1:k},z_{1:k-1})dx_{k-1} \end{aligned} \]按照线性假设,我们可以去除掉等式中的无关变量(化简等式):
- 对于条件概率(已知\(k-1\)时刻的后验和\(k\)时刻的输入值):由于\(\check{x}_{k-1}\)已经包含了\(u_{1:k-1}\)和\(z_{1:k-1}\),所以可以简化为:\(P(\hat{x}_k|\check{x}_{k-1},u_k)\);
- 对于\(k-1\)时刻后验概率:\(u_k\)不会影响到\(k-1\)的后验,即可化简为:\(P(\check{x}_{k-1}|x_0,u_{1:k-1},z_{1:k-1})\);
马尔科夫链即为:\(P(\hat{x}_k|x_0,u_{1:k},z_{1:k-1},z_{k})\varpropto P(z_k|\hat{x}_k)·\int{P(\hat{x}_k|\check{x}_{k-1},u_k)}P(\check{x}_{k-1}|x_0,u_{1:k-1},z_{1:k-1})dx_{k-1}\)。由于是正比关系,所以我们可以假设运动方程和观测方程均可服从线性表出(\(u_k\)可以忽略):
\[\begin{cases} \hat{x}_k=A_k\check{x}_{k-1}+u_k+w_k \\\\ z_k=C_k\hat{x}_k+v_k \end{cases} ,其中噪声服从高斯分布: \begin{cases} w_k\sim N(0,R_k) \\\\ v_k\sim N(0,Q_k) \end{cases} \]- 记\(k\)时刻\(x_k\)的先验概率分布为\(\hat{X}_k\sim N(\hat{\mu}_k,\hat{\Sigma}_k)\)、后验概率分布为\(\check{X}_k\sim N(\check{\mu}_k,\check{\Sigma}_k)\);
- 由于在观测时必须基于先验数据,所以此时的先验数据将会坍塌,不确定性随之消失,也就是说此时的未知量\(\hat{x}_k=x_k\sim N(x_k,0)\)(是一个常向量),所以可记\(k\)时刻似然概率分布为\(Z_k\sim N(C_kx_k,Q_k)\);
由随机变量函数的概率分布函数计算公式,可以得出:
\[\begin{cases} \hat{\mu}_k=A_k\check{\mu}_{k-1}+u_k \\ \hat{\Sigma}_k=A_k\check{\Sigma}_{k-1}A_k^T+R_k \end{cases} \]然后由于都是服从高斯分布,所以我们可以只对比指数即可(指数就是马氏距离,类似于二次型),对于先验后验的位姿参数\(x_k\)不做符号上的区分,因为已经在均值向量和协方差矩阵上体现出了分布差异,且本质上都是对位姿参数的分布解释,故统一用符号\(x_k\)表示。
\[\begin{aligned} 后验概率分布:&{(x_k-\check{\mu}_k)}^T·\check{\Sigma}_k^{-1}·{(x_k-\check{\mu}_k)} \\ 似然概率分布:&{(z_k-C_kx_k)}^T·Q_k^{-1}·{(z_k-C_kx_k)} \\ 先验概率分布:&{(x_k-\hat{x}_k)}^T·\hat{\Sigma}_k^{-1}·{(x_k-\hat{x}_k)} \end{aligned} \]在指数层面观察,后验概率分布 = 似然概率分布 + 先验概率分布,即有如下等式:
\[\small{\begin{aligned} {(x_k-\check{\mu}_k)}^T·\check{\Sigma}_k^{-1}·{(x_k-\check{\mu}_k)} &={(z_k-C_kx_k)}^T·Q_k^{-1}·{(z_k-C_kx_k)}+{(x_k-\hat{\mu}_k)}^T·\hat{\Sigma}_k^{-1}·{(x_k-\hat{\mu}_k)} \\ {(x_k^T-\check{\mu}_k^T)}·\check{\Sigma}_k^{-1}·{(x_k-\check{\mu}_k)}&={(z_k^T-x_k^TC_k^T)}·Q_k^{-1}·{(z_k-C_kx_k)}+{(x_k^T-\hat{\mu}_k^T)}·\hat{\Sigma}_k^{-1}·{(x_k-\hat{\mu}_k)} \end{aligned}} \]\[\begin{aligned} 等是左边=&{(x_k^T-\check{\mu}_k^T)}·\check{\Sigma}_k^{-1}·{(x_k-\check{\mu}_k)} \\=& \underbrace{x_k^T·\check{\Sigma}_k^{-1}·x_k}_{二次项} \underbrace{-x_k^T·\check{\Sigma}_k^{-1}·\check{\mu}_k-\check{\mu}_k^T·\check{\Sigma}_k^{-1}·x_k}_{一次项} \underbrace{+\check{\mu}_k^T·\check{\Sigma}_k^{-1}·\check{\mu}_k}_{常数项} \\ 等式右边=&{(z_k^T-x_k^TC_k^T)}·Q_k^{-1}·{(z_k-C_kx_k)}+{(x_k^T-\hat{\mu}_k^T)}·\hat{\Sigma}_k^{-1}·{(x_k-\hat{\mu}_k)} \\ =& z_k^T·Q_k^{-1}·z_k -z_k^T·Q_k^{-1}·C_kx_k -x_k^TC_k^T·Q_k^{-1}·z_k +x_k^TC_k^T·Q_k^{-1}·C_kx_k \\& +x_k^T·\hat{\Sigma}_k^{-1}·x_k -x_k^T·\hat{\Sigma}_k^{-1}·\hat{\mu}_k -\hat{\mu}_k^T·\hat{\Sigma}_k^{-1}·x_k +\hat{\mu}_k^T·\hat{\Sigma}_k^{-1}·\hat{\mu}_k \\ =& \underbrace{+x_k^TC_k^T·Q_k^{-1}·C_kx_k+x_k^T·\hat{\Sigma}_k^{-1}·x_k}_{二次项} \\ & \underbrace{-z_k^T·Q_k^{-1}·C_kx_k-x_k^TC_k^T·Q_k^{-1}·z_k-x_k^T·\hat{\Sigma}_k^{-1}·\hat{\mu}_k-\hat{\mu}_k^T·\hat{\Sigma}_k^{-1}·x_k}_{一次项} \\ & \underbrace{z_k^T·Q_k^{-1}·z_k+\hat{\mu}_k^T·\hat{\Sigma}_k^{-1}·\hat{\mu}_k}_{常数项} \\=& \underbrace{x_k^T·{(C_k^TQ_k^{-1}C_k+\hat{\Sigma}_k^{-1})}·x_k}_{二次项} \\& \underbrace{-[(z_k^TQ_k^{-1}C_k+\hat{\mu}_k^T\hat{\Sigma}_k^{-1})·x_k+x_k^T·(C_k^TQ_k^{-1}z_k+\hat{\Sigma}_k^{-1}\hat{\mu}_k)]}_{一次项} \\& \underbrace{z_k^T·Q_k^{-1}·z_k+\hat{\mu}_k^T·\hat{\Sigma}_k^{-1}·\hat{\mu}_k}_{常数项} \end{aligned} \]所以对应幂次相等原则,可得如下等式:
\[\begin{cases} 二次项:&\check{\Sigma}_k^{-1}=C_k^TQ_k^{-1}C_k+\hat{\Sigma}_k^{-1} \\\\ 一次项:& \small{-x_k^T\check{\Sigma}_k^{-1}\check{\mu}_k-\check{\mu}_k^T\check{\Sigma}_k^{-1}x_k = -x_k^T(C_k^TQ_k^{-1}z_k+\hat{\Sigma}_k^{-1}\hat{\mu}_k) -(z_k^TQ_k^{-1}C_k+\hat{\mu}_k^T\hat{\Sigma}_k^{-1})x_k} \\\\ 常数项:&\check{\mu}_k^T\check{\Sigma}_k^{-1}\check{\mu}_k=z_k^TQ_k^{-1}z_k+\hat{\mu}_k^T\hat{\Sigma}_k^{-1}\hat{\mu}_k \end{cases} \]-
比较二次项系数得后验协方差与先验协方差之间的关系
- 等式两边同时左乘\(\check{\Sigma}_k\):\(I=\check{\Sigma}_kC_k^TQ_k^{-1}C_k+\check{\Sigma}_k\hat{\Sigma}_k^{-1}\);
- 代入卡尔曼增益:\(I=KC_k+\check{\Sigma}_k\hat{\Sigma}_k^{-1}\);
- 整理得协方差关系:\(\check{\Sigma}_k=(I-KC_k)\hat{\Sigma}_k\);
【注】可利用\(\mbox{SWM(Sherman-Morrison-Woodbury)}\)恒等式解出\(K\),该方法可破解循环定义问题。
\[\begin{aligned} &K=\check{\Sigma}_kC_k^TQ_k^{-1}=(C_k^TQ_k^{-1}C_k+\hat{\Sigma}_k^{-1})^{-1}C_k^TQ_k^{-1}\\ &由SMW恒等式:AB{(D+CAB)}^{-1}\equiv {(A^{-1}+BD^{-1}C)}^{-1}BD^{-1}\\ &令A=\hat{\Sigma}_k,B=C_k^T,C=C_k,D=Q_k,可得:\\ &K=(C_k^TQ_k^{-1}C_k+\hat{\Sigma}_k^{-1})^{-1}C_k^TQ_k^{-1}=\hat{\Sigma}_kC_k^T{(Q_k+C_k\hat{\Sigma}_kC_k^T)}^{-1}\\ &即证:K=\check{\Sigma}_kC_k^TQ_k^{-1}\equiv \hat{\Sigma}_kC_k^T{(Q_k+C_k\hat{\Sigma}_kC_k^T)}^{-1},\small{卡尔曼增益可由先验算得} \end{aligned} \] -
比较一次项系数得后验均值与先验均值之间的关系
- 常数和协方差的转置都是本身:\(-2\check{\mu}_k^T\check{\Sigma}_k^{-1}x_k=-2(z_k^TQ_k^{-1}C_k+\hat{\mu}_k^T\hat{\Sigma}_k^{-1})x_k\);
- 取\(x_k\)的系数并转置:\(\check{\Sigma}_k^{-1}\check{\mu}_k=C_k^TQ_k^{-1}z_k+\hat{\Sigma}_k^{-1}\hat{\mu}_k\);
- 等式左右两边同时左乘\(\check{\Sigma}_k\):\(\check{\mu}_k=\check{\Sigma}_kC_k^TQ_k^{-1}z_k+\check{\Sigma}_k\hat{\Sigma}_k^{-1}\hat{\mu}_k\);
- 代入卡尔曼增益和协方差关系:\(\check{\mu}_k=\hat{\mu}_k+K(z_k-C_k\hat{\mu}_k)=\hat{\mu}_k+Kv_k\);
【注】所以该关系的意义就是“后验均值”就是“先验均值”加上一个修正量,而这个修正量就是对观测噪音(误差)做一个卡尔曼增益旋转(左乘为向量旋转,右乘为坐标系旋转)。
总结一下,我们通过定义了一个叫“卡尔曼增益”的中间变量建立起了(1)协方差矩阵的先后验概率关系(2)均值的先后验概率关系。于是我们可以将“后验 = 似然 × 先验”的过程分解为两个步骤:
-
预测(通过前一时刻的后验估计当前时刻的先验)
\[\begin{cases} \hat{\mu}_k=A_k\check{\mu}_{k-1}+u_k \\ \hat{\Sigma}_k=A_k\check{\Sigma}_{k-1}A_k^T+R \end{cases} \]
-
更新(通过卡尔曼增益更新先验从而得到后验)
\[\begin{cases} \check{\mu}_k=\hat{\mu}_k+K(z_k-C_k\hat{\mu}_k) \\ \check{\Sigma}_k=(I-KC_k)\hat{\Sigma}_k \end{cases} \]
-
-
非线性系统和\(\mbox{EKF(Extended Kalman Filter)}\)【对KF扩展至一阶】
推到过程与\(\mbox{KF}\)类似,只是核心思想有些微差异。\(\mbox{EKF}\)是对\(\mbox{KF}\)在\(\check{x}_{k-1}=\check{\mu}_{k-1}\)处和\(\hat{x}_k=\hat{\mu}_k\)的一阶泰勒展开:
\[\begin{aligned} &\begin{cases} \hat{x}_k\approx f(\check{\mu}_{k-1},u_k)+\frac{\part{f}}{\part{\check{x}_{k-1}}}|_{\check{x}_{k-1}=\check{\mu}_{k-1}}·(\check{x}_{k-1}-\check{\mu}_{k-1})+w_k \\ z_k\approx h(\hat{\mu}_k)+\frac{\part{h}}{\part{\hat{x}_k}}|_{\hat{x}_k=\hat{\mu}_k}·(\hat{x}_k-\hat{\mu}_k)+v_k \end{cases} \\\\ &记F= \frac{\part{f}}{\part{\check{x}_{k-1}}}|_{\check{x}_{k-1}=\check{\mu}_{k-1}},H=\frac{\part{h}}{\part{\hat{x}_k}}|_{\hat{x}_k=\hat{\mu}_k} \\\\ &\begin{cases} \hat{x}_k\approx F\underbrace{(\check{x}_{k-1}-\check{\mu}_{k-1})}_{\sim N(0,\check{\Sigma}_{k-1})}+\underbrace{w_k}_{\sim N(0,R)}+\underbrace{f(\check{\mu}_{k-1},u_k)}_{常数项} &\sim \small{N(f(\check{\mu}_{k-1},u_k),F\check{\Sigma}_{k-1}F^T+R_k)} \\\\ z_k\approx H\underbrace{(\hat{x}_k-\hat{\mu}_k)}_{\sim N(0,\hat{\Sigma}_k)}+\underbrace{v_k}_{\sim N(0,Q_k)}+\underbrace{h(\hat{\mu}_k)}_{常数项} &\sim N(h(\hat{\mu}_k),H\hat{\Sigma}_kH^T+Q_k) \end{cases} \end{aligned} \]然后贝叶斯展开并对比幂次系数可得:
\[\begin{cases} \check{\mu}_k=\hat{\mu}_k+K_k(z_k-h(\hat{\mu}_k)) \\\\ \check{\Sigma}_k=(I-K_kH)\hat{\Sigma}_k \end{cases} ,其中K_k为卡尔曼增益\overset{def}{=}\hat{\Sigma}_kH^T{(Q_k+H\hat{\Sigma}_kH^T)}^{-1} \]