标签：partial text sum SMNN beta 自旋空腔 prod sigma

引言

自旋玻璃模型是在研究相变问题时引入的一类统计物理模型，它的哈密顿量只包含晶格中不同格点上的自旋变量之间的相互作用。人们发现，铁磁相变、反铁磁相变等许多与磁性有关的二级相变都可以利用某种自旋玻璃模型进行刻画，超导相变、超流相变等其他二级相变的临界性质也可以与某个自旋玻璃模型的临界性质建立起对应关系，这表明自旋玻璃模型具有很好的普适性。[1]

在信息传输过程中，由于信道中存在噪声，信息可能会受到干扰而出现错误。从受干扰的消息中恢复原始信息是一项非常重要的任务。一种解决方案是在发送时对原始消息进行编码，引入冗余。然后接收方根据冗余来纠正一些传输错误。1948年，Claude Shannon证明了当码率低于信道容量时，无错传输是可能的，这为设计工程实用的编码方案建立了一个基本界限[2]。已经有很多人投入了大量的努力来设计接近香农界限(信道容量)的编码方案。其中，1989年Nicolas Sourlas提出一种编码方案[3]，它将纠错码与自旋玻璃模型联系起来，并且具有很高的性价比。

对于 $N$ 个二值信号构成的信源 $\boldsymbol{\xi} \in \{\pm 1\}^N$，Sourlas 编码的规则是随机选择一定数量的信号相乘，作为要传输的一个信号，即

\[J^0_a=\prod_{i\in \partial a}\xi_i \]

编码后的信息为 $\boldsymbol{J^0} = \{J^0_1, J^0_2, J^0_3, \cdots, J^0_M\}$；在传输过程中信号有 $p$ 的概率发生翻转，即$P(J_a|J_a^0)=p\delta(J_a+J_a^0)+(1-p)\delta(J_a-J_a^0)$，到达接收器的信息为 $\boldsymbol{J}=\{J_1, J_2, J_3, \cdots, J_M\}$。为了对信息 $\boldsymbol{J}$ 进行解码（将其恢复到 $\boldsymbol{\xi}$ ），我们首先将Sourlas码与自旋玻璃模型结合起来。

自旋玻璃模型的哈密顿量写为

\[H(\boldsymbol{\sigma})=-\sum_{a=1}^MJ_a\prod_{i\in\partial a}\sigma_i \]

此时这里的 $\sigma_i$ 是物理上的自旋，在信息传输问题中可以理解为原始信号 $\xi_i$。可以看到，这里自旋之间的局部相互作用与Sourlas码的编码规则相同，因此只有当 $\sigma_i$ 的取值与 $\xi_i$ 一一对应时，上式取最小值。哈密顿量取最小值正是我们在物理上希望的系统的稳态，此时各个格点变量的取值的期望用磁化强度 $m$ 表示。

这个系统的配分函数写为

\[Z=\mathrm{Tr~} \exp(-\beta H(\boldsymbol{\sigma})) \]

在下一小节中，我们利用空腔方法求解上式，并且由于配分函数 $Z$ 不是一个广延量，我们更关注的是作为广延量的自由能 $F=-\frac{1}{\beta}\ln Z$。因为空腔方法的核心就是利用cavity求出每个功能节点和变量节点的物理量，然后再将其相加得到总的待求物理量，这里就要求我们关注的必须是一个广延量。

空腔方法求解配分函数

首先介绍一下因子图，因子图是一类无向概率图模型, 包括变量节点和因子节点（或称为功能节点）。变量节点和功能节点之间用无向边连接。定义在因子图上的联合概率分布可以表示为各个因子的联乘积。

比如，对于一个服从下式的贝叶斯网络

\[p(I, D, G, S, L)=P(I) P(D) P(G \mid I, D) P(L \mid G) P(S \mid I) \]

实际上就是将一个联合概率分布 $p(I, D, G, S, L)$ 表达为多个局部的概率分布 $P(I)$、 $P(D)$、 $P(G \mid I, D)$、 $P(L \mid G)$、 $P(S \mid I)$ 的联乘。将各个概率分布抽象为一个函数，$f_I(I)$、 $f_D(D)$、 $f_G(G, I, D)$、 $f_S(L, G)$、 $f_L(S, I)$，在因子图中可以表示为

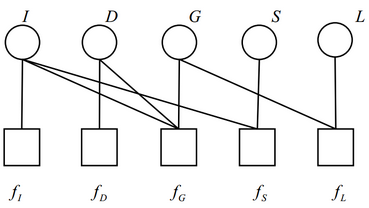
贝叶斯网络的因子图表示

对于自旋玻璃模型的哈密顿量，可以用因子图表示为

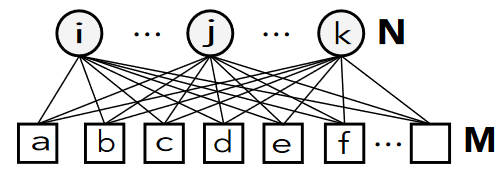
自旋玻璃模型的哈密顿的因子图表示

其中变量节点 $i,j,k,\cdots$表示哈密顿量中的dynamical binary spin variable，也即Sourlas码中的信号源 $\boldsymbol{\xi}\in \{\pm 1\}^N$，功能节点则表示一个连乘操作 $\prod_{i\in\partial a}$，每个功能节点与几个变量节点相连，正是Sourlas码的编码规则。

由于这是一个稀疏连接的网络，可以展开成树状图：

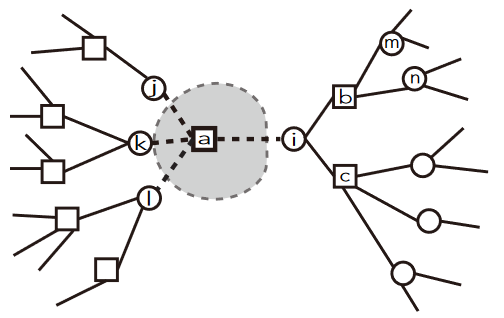
因子图展开为树状图

如上图所示，我们首先考虑将一个功能节点 $a$ 拿走，剩下的网络构成 $\text{old}$ 网络，然后再将 $a$ 加回去，作为 $\text{new}$ 网络。新旧网络的自由能差值即这个功能节点的自由能。新网络的哈密顿量可以写为

\[H^{\text{new} } = H^{\text{old} } - J_a\prod_{i\in \partial a} \sigma_i \]

因此配分函数可以写成：

\[\begin{aligned} &Z^{\text{new} } = \sum_{\{\sigma_i\} }\exp \left(-\beta H^{\text{old} }+\beta J_a \prod_{i \in \partial a} \sigma_i \right)\\ &=Z^{\text{old} } \sum_{\{\sigma_i\} }\left[\frac{\exp(-\beta H^{\text{old} })}{Z^{\text{old} } } \exp(\beta J_a \prod_{i \in \partial a} \sigma_i ) \right] \\ &=Z^{\text{old} } \sum_{\{\sigma_i | i \in \partial a \} }\sum_{\{\sigma_i | i \notin \partial a \} }\left[\frac{\exp(-\beta H^{\text{old} })}{Z^{\text{old} } } \exp(\beta J_a \prod_{i \in \partial a} \sigma_i ) \right] \\ &=Z^{\text{old} } \sum_{\{\sigma_i | i \in \partial a \} }\left[ \exp(\beta J_a \prod_{i \in \partial a} \sigma_i ) \sum_{\{\sigma_i | i \notin \partial a \} } \frac{\exp(-\beta H^{\text{old} })}{Z^{\text{old} } } \right] \end{aligned} \]

考虑后面一项 $\sum_{{\sigma_i | i \notin \partial a } } \frac{\exp(-\beta H^{\text{old} })}{Z^{\text{old} } } $ 的物理意义。如果求和号中 $\sigma_i$ 的指标 $i$ 是对旧网络中的所有节点，即 $\{\sigma_i|i\notin a\}$，那么这一项的意义是整个旧网络所有节点的联合概率分布。现在求和指标中去掉了边界上的点 $\{\sigma_i|i\in \partial a\}$，其表示的是边界点的边缘概率分布。

接着做一个“空腔假设”，把空腔的边缘概率分布认为是空腔的概率分布

\[P_{\text{Cavity} }(\{\sigma_i|i\in\partial a \}) = \sum_{\{\sigma_i | i \notin \partial a \} } \frac{\exp(-\beta H^{\text{old} })}{Z^{\text{old} } } \]

并且认为边界上各个节点是相互独立的。因此近似有

\[P_{\text{Cavity} }(\{\sigma_i|i\in\partial a \}) \approx \prod_{i\in\partial a} q_{i\to a}(\sigma_i) \]

写出节点 $i$ 上自旋变量取值的期望，即物理上的磁化强度 $m$ 为

\[m_{i\to a}=(+1)q_{i\to a}(\sigma_i = +1) + (-1)q_{i\to a}(\sigma_i = -1) \]

进而反写出节点概率的表达式

\[q_{i\to a}(\sigma) = \frac{1+\sigma_i m_{i\to a} }{2} \]

至此，由空腔概率和空腔假设得到

\[\sum_{\{\sigma_i | i \notin \partial a \} } \frac{\exp(-\beta H^{\text{old} })}{Z^{\text{old} } } \approx \prod_{i\in\partial a}\frac{1+\sigma_i m_{i\to a} }{2} \]

代入配分函数的展开式，得

\[Z^{\text{new} } =Z^{\text{old} } \sum_{\{\sigma_i | i \in \partial a \} }\left[ \exp(\beta J_a \prod_{i \in \partial a} \sigma_i ) \prod_{i\in\partial a}\frac{1+\sigma_i m_{i\to a} }{2}\right] \]

然后考虑将 $\prod_{i\in\partial a}\frac{1+\sigma_i m_{i\to a} }{2}$ 展开处理：

\[\begin{aligned} \prod_{i\in\partial a}\frac{1+\sigma_i m_{i\to a} }{2} &=\frac{1}{2^N}(1+\sigma_1 m_{1\to a})(1+\sigma_2 m_{2\to a})\cdots (1+\sigma_N m_{N\to a})\\ &=\frac{1}{2^N}( 1 + \sigma_1 m_{1\to a} + \sigma_2 m_{2\to a} + \cdots \\ &\;\,\,\qquad\quad + \sigma_1\sigma_2 m_{1\to a}m_{2\to a} + \sigma_1\sigma_3 m_{1\to a}m_{3\to a} + \cdots \\ &\;\,\,\qquad\quad + \cdots \\ &\;\,\,\qquad\quad + \prod_{i\in\partial a} \sigma_i \prod_{i\in\partial a} m_{i\to a}) \end{aligned} \]

在外面要对 $\{\sigma_i\}$ 做求和，可以确定 $\prod_{i\in\partial a}\sigma_i = \pm 1$。但是对于 $\sigma_1\sigma_2$，$\sigma_2\sigma_4\sigma_5$ 等中间项，可以写作 $\prod_{i\in D}\sigma_i= \prod_{i\in \partial a}\sigma_i / \prod_{i\in \partial a,i \notin D}\sigma_i $，这里 $\prod_{i\in \partial a,i \notin D}\sigma_i$ 的取号是不确定的（有可能是 $1$ 也有可能是 $-1$ ），因此对这个展开式做求和时只有第一项和最后一项会确定下来，其他项都会因为有 $+1$ 和 $-1$ 两种可能值而抵消掉。因此有

\[\prod_{i\in\partial a}\frac{1+\sigma_i m_{i\to a} }{2} =\frac{1}{2}(1+ \prod_{i\in\partial a} \sigma_i \prod_{i\in\partial a} m_{i\to a})=\frac{1}{2}(1+ \prod_{i\in\partial a} \sigma_i m_{i\to a}) \]

进而得到

\[\begin{aligned} Z^{\text{new} } &= Z^{\text{old} } \sum_{\{ {\prod_{i\in\partial a}\sigma_i} = \pm 1 \} }\left[ \exp(\beta J_a \prod_{i \in \partial a} \sigma_i )\frac{1}{2} (1+ \prod_{i\in\partial a} \sigma_i m_{i\to a})\right]\\ &=Z^{\text{old} }\left[ \exp(\beta J_a)\frac{1}{2} (1+ \prod_{i\in\partial a}m_{i\to a})+\exp(-\beta J_a)\frac{1}{2} (1- \prod_{i\in\partial a}m_{i\to a})\right]\\ &=Z^{\text{old} } \left[\frac{1}{2}[\exp(\beta J_a)+\exp(-\beta J_a)]+ \frac{1}{2}[\exp(\beta J_a)-\exp(-\beta J_a)]\prod_{i\in\partial a}m_{i\to a} \right]\\ &=Z^{\text{old} }\left[ \cosh(\beta J_a)+\sinh(\beta J_a)\prod_{i\in\partial a}m_{i\to a} \right] \\ &=Z^{\text{old} }\cosh(\beta J_a)\left(1+\tanh(\beta J_a)\prod_{i\in\partial a}m_{i\to a} \right) \end{aligned} \]

即配分函数经过空腔近似后最终化为

\[Z^{\text{new} }=Z^{\text{old} }\cosh(\beta J_a)\left(1+\tanh(\beta J_a)\prod_{i\in\partial a}m_{i\to a} \right) \]

考虑自由能的定义为

\[F\equiv -\frac{1}{\beta}\ln Z \]

因此加上一个功能节点后自由能的增量为

\[\Delta F_a=-\frac{1}{\beta}\ln \frac{Z^{\text{new} } }{Z^{\text{old} } }=\ln \left[\cosh(\beta J_a)\left(1+\tanh(\beta J_a)\prod_{i\in\partial a}m_{i\to a} \right)\right] \]

对于变量节点，采取同样的方法，但是在添加变量节点$i$的同时要将与其邻近的功能节点 $\{b|b\in \partial i\}$ 一起添加进网络中。配分函数的变化写为

\[Z^{\text{new} } = \sum_{\sigma_i^{\text{old} } }\sum_{\sigma_i}\exp \left(-\beta H^{\text{old} }+\beta \sum_{b\in \partial i} J_b \prod_{j \in \partial b} \sigma_j \right) \]

这里的 cavity 就包括了变量节点 $i$ 和与其邻近的功能节点 $\{b|b\in \partial i\}$。下面我们将上式中的 cavity 分离出来，然后将旧网络分离出来。

\[\begin{aligned} Z^{\text{new} } &= \sum_{\sigma_i^{\text{old} } }\sum_{\sigma_i}\exp \left(-\beta H^{\text{old} }+\beta \sum_{b\in \partial i} J_b \prod_{j \in \partial b} \sigma_j \right) \\ & = \sum_{\sigma_i^{\text{old} } }\sum_{\sigma_i}\exp \left[-\beta H^{\text{old} }+\beta \sum_{b\in \partial i} J_b \left(\sigma_i \prod_{j \in \partial b\textbackslash i} \sigma_j\right) \right]\\ &=Z^{\text{old} }\sum_{\sigma_i^{\text{old} } }\sum_{\sigma_i}\frac{\exp (-\beta H^{\text{old} })}{Z^{\text{old} } } \exp \left[\beta \sum_{b\in \partial i} J_b \left(\sigma_i \prod_{j \in \partial b\textbackslash i} \sigma_j\right) \right] \end{aligned} \]

将第一个求和号 $\sum_{\sigma_i^{\text{old} } }$ 中的指标分成属于 cavity 边缘的节点和其他的节点两部分，即 $\sum_{\sigma_i^{\text{old} } } = \sum_{\{\sigma_j | j \in \partial b\textbackslash i;b \in \partial i \} } + \sum_{\{\sigma_j | j \notin \partial b\textbackslash i;b \in \partial i \} }$。为了书写方便，以下写到 $j \in \partial b\textbackslash i$ 时默认 $b \in \partial i$。显然 $\sum_{\{\sigma_j | j \notin \partial b\textbackslash i\} }$ 这个求和在上式中只对 $\frac{\exp (-\beta H^{\text{old} })}{Z^{\text{old} } }$ 起作用，仿照之前的处理将其写为空腔概率：

\[P_{\text{cavity} }(\{\sigma_j | j \in \partial b\textbackslash i \}) = \sum_{\{\sigma_j | j \notin \partial b\textbackslash i \} } \frac{\exp(-\beta H^{\text{old} })}{Z^{\text{old} } } \approx \prod_{b \in \partial i}\prod_{j \in \partial b\textbackslash i} q_{j\to b}(\sigma_j) \]

类比之前的做法，有

\[q_{j\to b}(\sigma_j) = \frac{1+\sigma_jm_{j \to b} }{2} \]

因此配分函数写为

\[\begin{aligned} Z^{\text{new} } &= Z^{\text{old} }\sum_{\sigma_i^{\text{old} } }\sum_{\sigma_i}\frac{\exp (-\beta H^{\text{old} })}{Z^{\text{old} } } \exp \left[\beta \sum_{b\in \partial i} J_b \left(\sigma_i \prod_{j \in \partial b\textbackslash i} \sigma_j\right) \right] \\ &= Z^{\text{old} } \sum_{\{\sigma_j | j \in \partial b\textbackslash i\} } \sum_{\sigma_i} P_{\text{cavity} }(\{\sigma_j | j \in \partial b\textbackslash i \}) \exp \left[\beta \sum_{b\in \partial i} J_b \left(\sigma_i \prod_{j \in \partial b\textbackslash i} \sigma_j\right) \right]\\ &\approx Z^{\text{old} } \sum_{\{\sigma_j | j \in \partial b\textbackslash i\} } \sum_{\sigma_i} \prod_{b \in \partial i}\prod_{j \in \partial b\textbackslash i} q_{j\to b}(\sigma_j) \exp \left[\beta \sum_{b\in \partial i} J_b \left(\sigma_i \prod_{j \in \partial b\textbackslash i} \sigma_j\right) \right] \end{aligned} \]

交换一下求和号 $\sum_{\{\sigma_j | j \in \partial b\textbackslash i\} }$ 和累乘号 $\prod_{b \in \partial i}$ 的顺序，写为

\[Z^{\text{new} } \approx Z^{\text{old} } \sum_{\sigma_i} \prod_{b \in \partial i} \sum_{\{\sigma_j | j \in \partial b\textbackslash i \} } \prod_{j \in \partial b\textbackslash i} \frac{1+\sigma_jm_{j \to b} }{2} \exp \left[\beta \sum_{b\in \partial i} J_b \left(\sigma_i \prod_{j \in \partial b\textbackslash i} \sigma_j\right) \right] \]

对于 $\sum_{\{\sigma_j | j \in \partial b\textbackslash i \} } \prod_{j \in \partial b\textbackslash i} \frac{1+\sigma_jm_{j \to b} }{2} \exp \left[\beta \sum_{b\in \partial i} J_b \left(\sigma_i \prod_{j \in \partial b\textbackslash i} \sigma_j\right) \right]$ 采用与之前相同的一个trick（具体怎么操作待补充补充），可以化简得

\[Z^{\text{new} } \approx Z^{\text{old} } \left( \prod_{b \in \partial i} \Lambda^+_{b\to i} + \prod_{b \in \partial i} \Lambda^-_{b\to i} \right) \]

其中，

\[\Lambda^\pm_{b\to i} =\cosh(\beta J_b)\left( 1\pm \tanh(\beta J_b) \prod_{j \in \partial b\textbackslash i} m_{j\to b} \right) \label{eq:Lambda^pm的定义} \]

写出自由能的变化量为

\[\Delta F_i = -\frac{1}{\beta}\ln \frac{Z^{\text{new} } }{Z^{\text{old} } }=\ln \left[ \prod_{b \in \partial i} \Lambda^+_{b\to i} + \prod_{b \in \partial i} \Lambda^-_{b\to i} \right] \]

至此，已经得到了加上一个功能节点和一个变量节点时自由能的变化量，即

\[\begin{aligned} &\Delta F_a=-\frac{1}{\beta}\ln \frac{Z^{\text{new} } }{Z^{\text{old} } }=\ln \left[\cosh(\beta J_a)\left(1+\tanh(\beta J_a)\prod_{i\in\partial a}m_{i\to a} \right)\right]\\ &\Delta F_i = -\frac{1}{\beta}\ln \frac{Z^{\text{new} } }{Z^{\text{old} } }=\ln \left[ \prod_{b \in \partial i} \Lambda^+_{b\to i} + \prod_{b \in \partial i} \Lambda^-_{b\to i} \right] \end{aligned} \]

求系统的总自由能即相当于求加上各个节点时自由能的变化量之和，但是注意在计算变量节点的自由能时将与其临近的功能节点也算入了，因此要减掉重复了$|\partial a|$次的对每个功能节点的求和，即

\[F = \sum_{i} \Delta F_i + \sum_{a} \Delta F_a - \sum_{a} |\partial a| \Delta F_a \]

注意到，这里的$\Lambda^{\pm}_{b\to i}$在定义时用到了$m_{j\to b}$，下一小节我们介绍如何迭代求解。

消息传递算法

空腔磁化强度 在空腔方法中，首先定义cavity magnetization $m_{i\to a}$，即变量节点 $i$ 和功能节点$a$之间的连接不存在时，节点 $i$ 的磁化强度

\[m_{i\to a}=\frac{\sum_{\sigma}\sigma_i\exp{-\beta H_{i\to a}(\boldsymbol{\sigma})} }{\sum_{\sigma}\exp{-\beta H_{i\to a}(\boldsymbol{\sigma})} } \label{eq:空腔磁化强度的定义} \]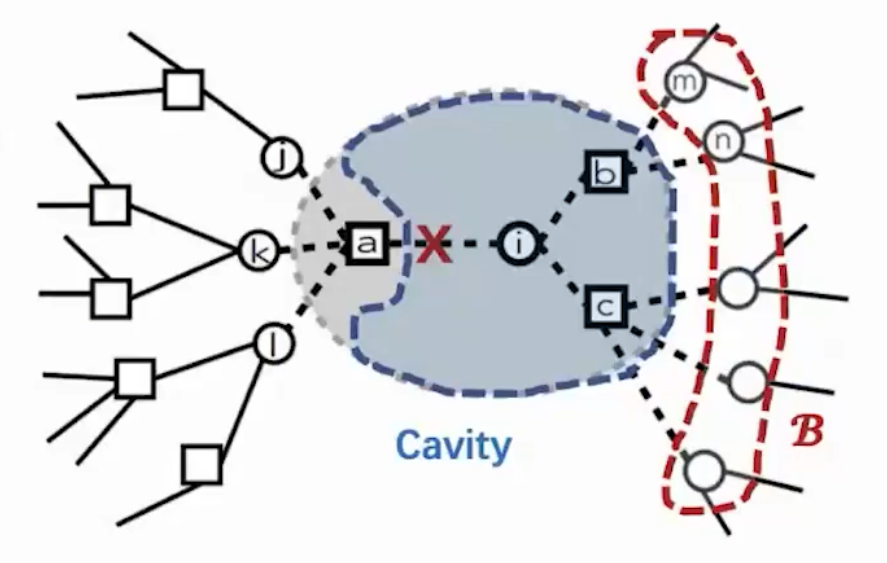

空腔磁化强度示意图

其中，$H_{i \rightarrow a}$ 是指把节点 $a$ 拿掉后节点 $i$ 的哈密顿量，

\[H_{i \rightarrow a}=H_{\text {cavity } }-\sum_{b \in \partial i \backslash a} J_b \sigma_i \prod_{j \in \partial b \backslash i} \sigma_j \]

$H_{\text {cavity } }$是指 cavity 内所有节点作为一个系统的哈密顿量，它包含了上图中 $b$、$c$ 等节点与 cavity 外界的连接，即用红线围起来的边界部分 $\mathcal{B}$。求 $H_{i \rightarrow a}$ 时要从 $H_{\text {cavity } }$ 中减去 cavity 与 $\mathcal{B}$ 连接的部分。我们将空腔磁化强度的定义做一个trick，

\[m_{i\to a}=\frac{\sum_{\sigma}\sigma_i\exp{-\beta H_{i\to a}(\boldsymbol{\sigma})} }{\sum_{\sigma}\exp{-\beta H_{i\to a}(\boldsymbol{\sigma})} }=\frac{\frac{\sum_\sigma \sigma_i \exp \left(-\beta H_{i \rightarrow a}(\sigma)\right)}{Z_{\text {cavity } } } }{\frac{\sum_\sigma \exp \left(-\beta H_{i \rightarrow a}(\sigma)\right)}{Z_{\text {cavity } } } } \]

然后做一个与上一小节类似的空腔假设，

\[\begin{aligned} \frac{\sum_\sigma \exp \left(-\beta H_{i \rightarrow a}(\sigma)\right)}{Z_{\text {cavity } } } &= \frac{\sum_\sigma \exp \left[-\beta \left( H_{\text {cavity } }-\sum_{b \in \partial i \backslash a} J_b \sigma_i \prod_{j \in \partial b \backslash i} \sigma_j \right) \right]}{Z_{\text {cavity } } }\\ &=\frac{\sum_\sigma \exp(-\beta H_{\text {cavity } }) \exp \left(\beta \sum_{b \in \partial i \backslash a} J_b \sigma_i \prod_{j \in \partial b \backslash i} \sigma_j \right)}{Z_{\text {cavity } } } \end{aligned} \]

注意到 $\frac{\exp(-\beta H_{\text {cavity } })}{Z_{\text {cavity } } }$ 正是 cavity 的联合概率分布，根据空腔假设，其等于 cavity 的边缘概率分布，

\[\frac{\exp(-\beta H_{\text {cavity } })}{Z_{\text {cavity } } } = P_{\text {cavity } }(\mathcal{B}) \approx \prod_{b \in \partial i \backslash a} \prod_{j \in \partial b \backslash i} q_{j \rightarrow b}\left(\sigma_j\right) \]

因此可得

\[m_{i\to a}=\frac{\sum_{\sigma_i} \sum_{\mathcal{B} } \sigma_i P_{\text {cavity } }(\mathcal{B}) \exp \left(\beta \sum_{b \in \partial i \backslash a} J_b \sigma_i \prod_{j \in \partial b \backslash i} \sigma_j\right)}{\sum_{\sigma_i} \sum_{\mathcal{B} } P_{\text {cavity } }(\mathcal{B}) \exp \left(\beta \sum_{b \in \partial i \backslash a} J_b \sigma_i \prod_{j \in \partial b \backslash i} \sigma_j\right)} \]

这里将对自旋变量的求和分为节点 $i$ 和边界 $\mathcal{B}$ 两部分，然后再使用与之前类似的操作，注意到

\[P_{\text {cavity } }(\mathcal{B}) \approx \prod_{b \in \partial i \backslash a} \prod_{j \in \partial b \backslash i} q_{j \rightarrow b}\left(\sigma_j\right)=\prod_{b \in \partial i \backslash a} \prod_{j \in \partial b \backslash i} \frac{1+\sigma_j m_{j\to b} }{2} \]

因此 $\sum_{\sigma_i} \sum_{\mathcal{B} } P_{\text {cavity } }(\mathcal{B}) \exp \left(\beta\sum_{b \in \partial i \backslash a} J_b \sigma_i \prod_{j \in \partial b \backslash i} \sigma_j\right)$ 可以整理成

\[\begin{aligned} &\quad\sum_{\sigma_i} \sum_{\mathcal{B} } \prod_{b \in \partial i \backslash a} \prod_{j \in \partial b \backslash i} \frac{1+\sigma_j m_{j\to b} }{2} \exp \left[ \beta\sum_{b \in \partial i \backslash a} J_b \left( \sigma_i \prod_{j \in \partial b \backslash i}\right) \sigma_j\right]\\ &=\sum_{\sigma_i}\prod_{b \in \partial i \backslash a}\sum_{\mathcal{B} }\prod_{j \in \partial b \backslash i}\frac{1+\sigma_j m_{j\to b} }{2} \exp \left[ \beta\sum_{b \in \partial i \backslash a} J_b \left( \sigma_i \prod_{j \in \partial b \backslash i}\right) \sigma_j\right] \end{aligned} \]

这与上一小节不能说是十分相似，只能说是一模一样。经过相同的trick后得到

\[m_{i \rightarrow a}=\frac{\prod_{b \in \partial i \backslash a} \Lambda_{b \rightarrow i}^{+}-\prod_{b \in \partial i \backslash a} \Lambda_{b \rightarrow i}^{-} }{\prod_{b \in \partial i \backslash a} \Lambda_{b \rightarrow i}^{+}+\prod_{b \in \partial i \backslash a} \Lambda_{b \rightarrow i}^{-} } \]

其中，

\[\Lambda^\pm_{b\to i} =\cosh(\beta J_b)\left( 1\pm \tanh(\beta J_b) \prod_{j \in \partial b\textbackslash i} m_{j\to b} \right) \]

共轭空腔磁化强度 定义空腔磁化强度 $m_{j\to b}$ 的 conjugate cavity magnetization为

\[\hat{m}_{b \rightarrow j} \equiv \tanh \left(\beta J_b\right) \prod_{j \in \partial b \backslash i} m_{j \rightarrow b} \]

因此空腔磁化强度表达式可以写为

\[m_{i \rightarrow a}=\frac{\prod_{b \in \partial i \backslash a}\left(1+\hat{m}_{b \rightarrow i}\right)-\prod_{b \in \partial i \backslash a}\left(1-\hat{m}_{b \rightarrow i}\right)}{\prod_{b \in \partial i \backslash a}\left(1+\hat{m}_{b \rightarrow i}\right)+\prod_{b \in \partial i \backslash a}\left(1-\hat{m}_{b \rightarrow i}\right)} \]

接下来采用了一种我现在还不能理解的参数化，即

\[\begin{aligned} q_{i \rightarrow a}\left(\sigma_i\right) & \equiv \frac{\exp \left(\beta h_{i \rightarrow a} \sigma_i\right)}{2 \cosh \beta h_{i \rightarrow a} } =\frac{1+\sigma_i m_{i \rightarrow a} }{2}\\ p_{a \rightarrow i}\left(\sigma_i\right) & \equiv \frac{\exp \left(\beta u_{a \rightarrow i} \sigma_i\right)}{2 \cosh \beta u_{a \rightarrow i} }=\frac{1+\sigma_i \hat{m}_{a \rightarrow i} }{2} \end{aligned} \]

得到

\[\begin{aligned} m_{i \rightarrow a} &=\tanh \beta h_{i \rightarrow a} \\ \hat{m}_{a \rightarrow i} &=\tanh \beta u_{a \rightarrow i} \end{aligned} \]

代入上面两式，得

\[\begin{aligned} &h_{i \rightarrow a}=\frac{1}{\beta}\left(\sum_{b \in \partial i \backslash a} \beta u_{b \rightarrow i}\right) \\ &u_{a \rightarrow i}=\frac{1}{\beta} \tanh ^{-1}\left[\tanh \left(\beta J_a\right) \prod_{j \in \partial a \backslash i} \tanh \left(\beta h_{j \rightarrow a}\right)\right] \end{aligned} \]

这是一个迭代式，通过迭代求解 $u_{b \rightarrow i}$ 后，再通过下式即可求解 $m_i$

\[m_i=\tanh \left(\sum_{b \in \partial i} \beta u_{b \rightarrow i}\right) \]

注意到 $m_i$ 实际上就是 $\sigma_i$ 的期望，因此通过 $m_i$ 进行解码的规则很简单：若 $m_i>0$ 则认为 $\sigma_i=1$；若 $m<0$ 则认为 $\sigma_i=-1$。这被称为最大后验边缘概率（maximizer of the posterior marginal, MPM），即

\[\sigma_i=\arg \max _{\sigma_i} P_i\left(\sigma_i\right) \]

拓展阅读与应用举例

空腔方法在RNN中的应用

（待补充）

作业

Assignment 1

Use cavity method to calculate the free energy and magnetization of the Sherrington-Kirkpatrick (SK) model, and compare the result with numerical enumeration.

Assignment 2

a: Write a program to implement the encoding and decoding scheme in Sourlas code system $\left(K \equiv|\partial a|=3, \mathrm{R} \equiv \frac{N}{M}=0.5\right)$.

b: Then show how the decoding performance changes with the flipping rate $p$ at a special temperature $\beta_p=\frac{1}{2} \ln \frac{1-p}{p}$.

参考文献

[1] 刘川. 热力学与统计物理[M]. 北京：北京大学出版社，2022：172-173.

[2] Shannon, C. E. A Mathematical Theory of Communication[J]. Bell Systems Technical Journal, 1948, 27(4):623-656.

[3] Sourlas, Nicolas. Spin-glass models as error-correcting codes[J]. Nature, 1989, 339(6227):693-695.

标签：partial,text,sum,SMNN,beta,自旋,空腔,prod,sigma
From： https://www.cnblogs.com/lyhspace/p/17003818.html

【SMNN】自旋玻璃与空腔方法

引言