倍增法求最近公共祖先

title: 倍增法求最近公共祖先
date: 2022-11-15 10:31:45
tags: 算法

本文章遵守知识共享协议 CC-BY-NC-SA ，转载时须在文章的任一位置附上原文链接和作者署名（rickyxrc）。推荐在我的个人博客阅读。

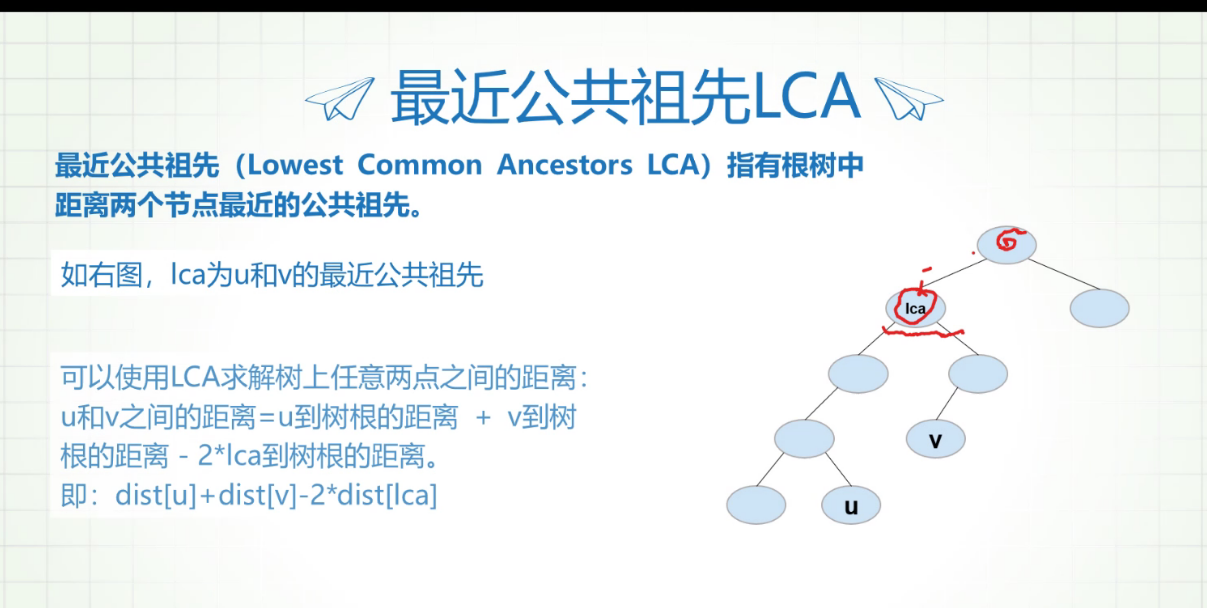
最近公共祖先（Lowest Common Ancestors，一般称作LCA）指有根树中距离两个节点最近的公共祖先。

前置知识

• 多叉树

在使用倍增之前，求公共祖先的方法(暴力算法)：

向上标记法

从A向根节点遍历，记录每个节点，

然后B向根节点遍历，遇到标记过的节点就结束。

同步前进法

将A,B中较深的节点走到同一深度，然后一起向上直到走到同一节点。

树上倍增法（主角）

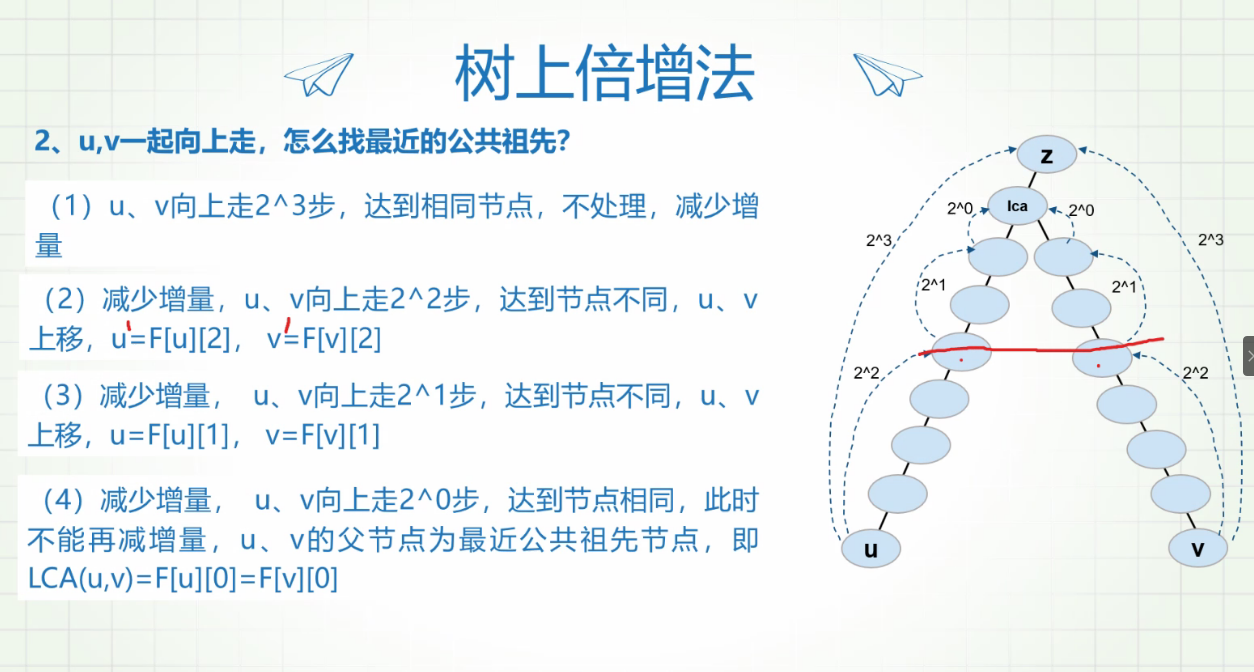
修正：表示j的 \(2^i\) 辈祖先。

（与ST有异曲同工之妙）

数据结构

std::vector<int> edge[maxn];//链式前向星
int depth[maxn],//节点的深度
    fath[maxn][32];//父亲节点，类似于ST表

初始化LCA

void initLCA(int index, int father)
{
    fath[index][0] = father;
    depth[index] = depth[father] + 1;
    int k = log2(depth[index]) + 1;
    for (int i = 0; i < k; i++)
        fath[index][i] = fath[fath[index][i - 1]][i - 1];
    for (auto t : edge[index])
        if (father != t)
            initLCA(t, index);
}

步骤：

• 将A,B移动到同一深度
• 向上倍增：

将A和B移动到同一深度

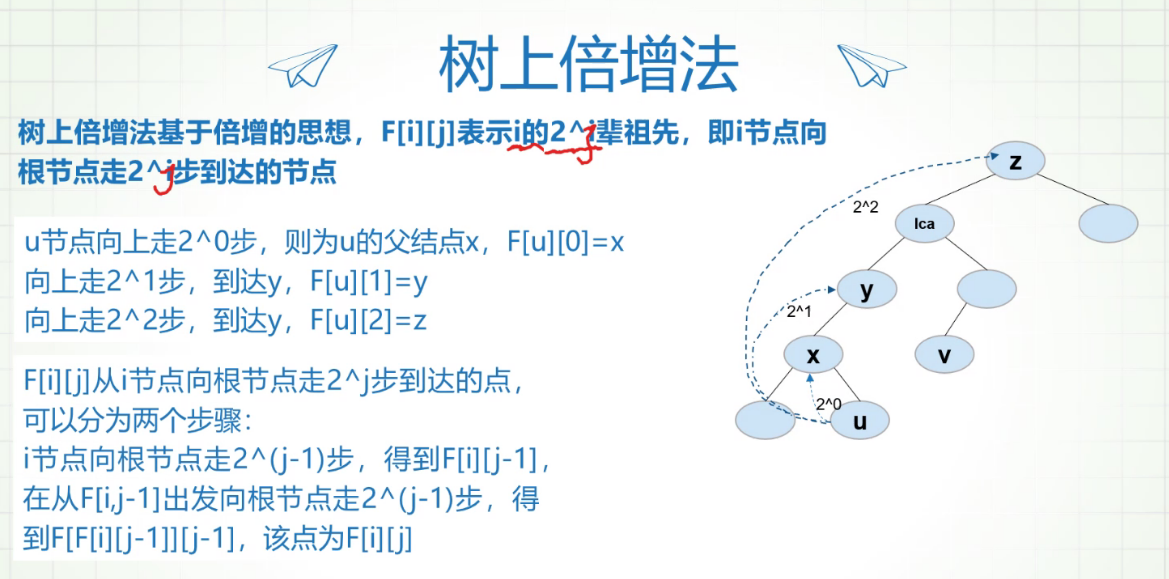
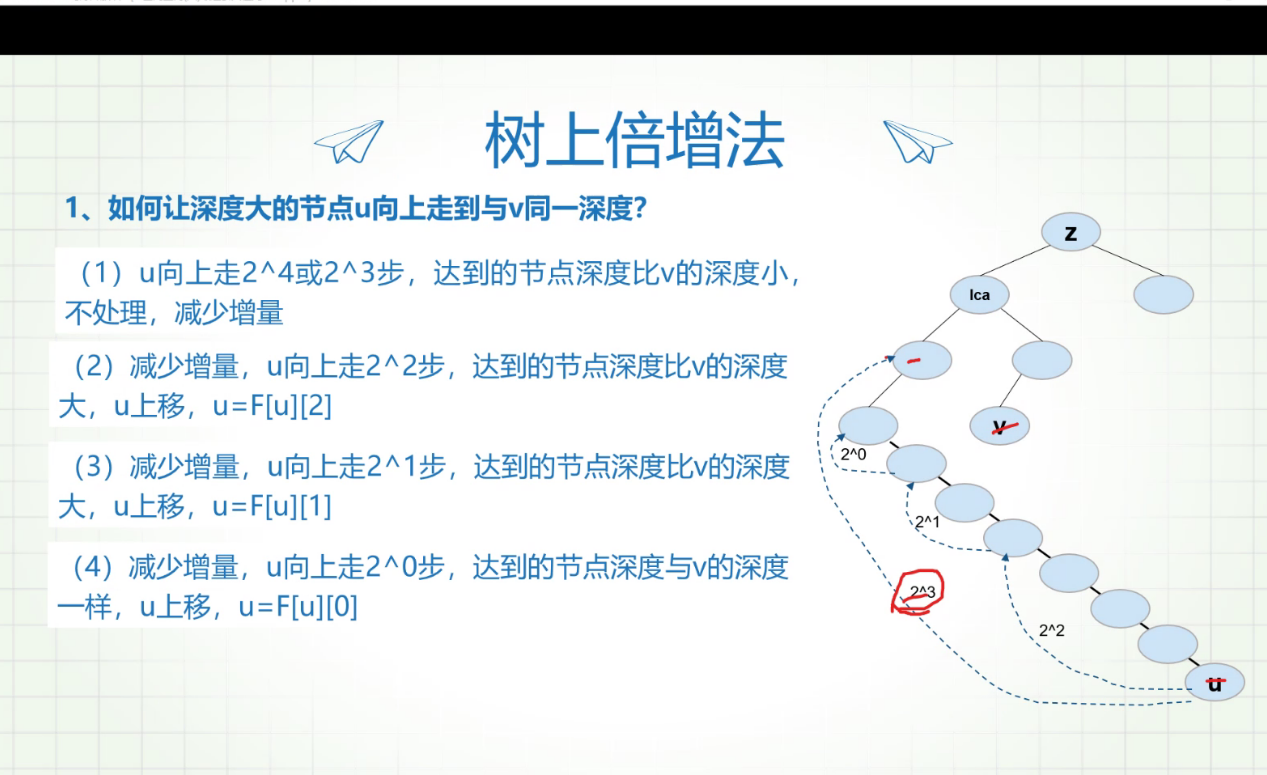
代码如下：

int queryLCA(int nodeA, int nodeB)
{
    if (depth[nodeA] < depth[nodeB])
        return queryLCA(nodeB, nodeA); // 先颠倒顺序
    while (depth[nodeA] > depth[nodeB]) // 将较深的节点跳到相同层
    {
        int __t = log2(depth[nodeA] - depth[nodeB]);
        nodeA = fath[nodeA][__t];
    }
    if (nodeA == nodeB) // 如果已经在一起了
        return nodeA;
    for (int jmp = log2(depth[nodeA]); jmp >= 0; jmp--) //往上跳相同的层级
    {
        if (fath[nodeA][jmp] != fath[nodeB][jmp])
            nodeA = fath[nodeA][jmp],
            nodeB = fath[nodeB][jmp];
    }
    return fath[nodeA][0];
}

模板题目及解析

P3379-【模板】最近公共祖先-LCA

这道题一看就是裸的LCA，直接打板子就行。