代码随想录算法训练营Day22|235. 二叉搜索树的最近公共祖先、701. 二叉搜索树中的插入操作、450. 删除二叉搜索树中的节点
235. 二叉搜索树的最近公共祖先
首先题目要求:
- 所有节点的值都是唯一的。
- p、q 为不同节点且均存在于给定的二叉搜索树中。
这说明我们可以通过数值唯一确定每个节点,并且排除了异常输入的考虑。
①二叉树常规做法
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode(int x) : val(x), left(NULL), right(NULL) {}
* };
*/
class Solution {
public:
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
// 递归终止条件
// if (root == NULL) return NULL;
// if (root == p || root == q) return root;
if (root == NULL || root == p || root == q) return root;
TreeNode* left = lowestCommonAncestor(root->left, p, q);
TreeNode* right = lowestCommonAncestor(root->right, p, q);
if (left != NULL && right != NULL) return root;
// 如果只有一边有返回节点
else if (left != NULL && right == NULL) return left;
else return right;
}
};
②利用二叉搜索树的特性
由于BST的特性,公共祖先的数值肯定在[p, q]范围内:这意味着,当遍历到节点数值在[p, q]范围内时,就可以确定其为公共祖先。
目前的问题是首次遇见的公共祖先节点是否为「最近公共祖先节点」?
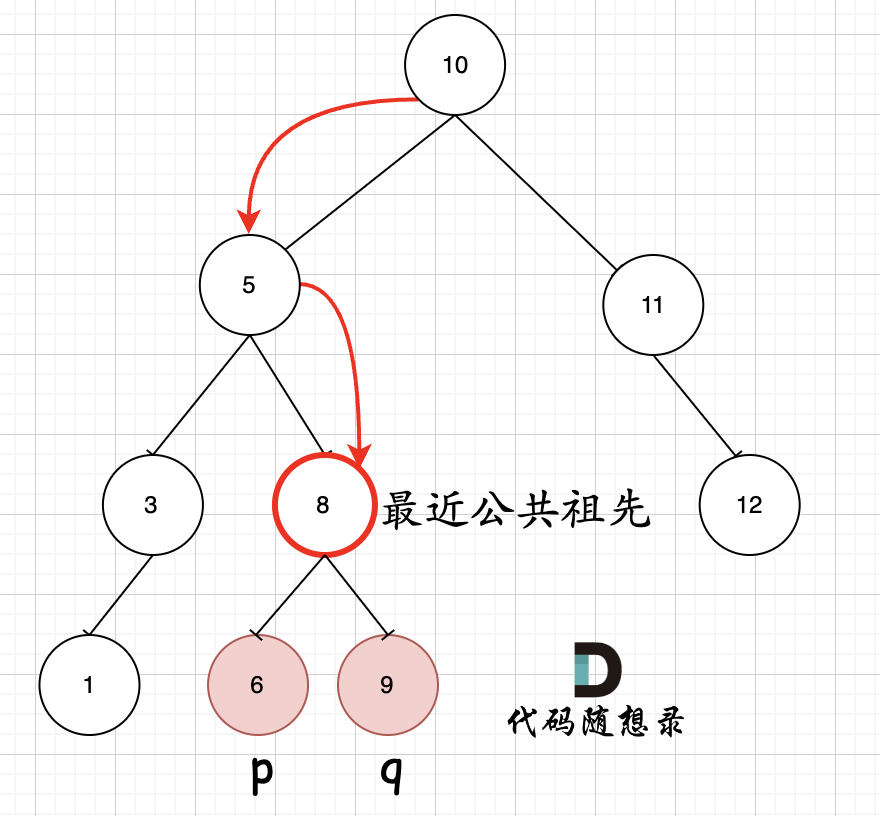
图中能看出,使用从上到下的遍历方法获得的首个节点即为「最近公共祖先」。因此不需要遍历整棵树,只需要遍历分支,在遇到合适的节点后立即返回即可。代码如下:
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode(int x) : val(x), left(NULL), right(NULL) {}
* };
*/
class Solution {
public:
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
if (root == NULL) return NULL;
// 规范给定节点的数值大小
if (p->val > q->val) swap(p, q);
if (root->val >= p->val && root->val <= q->val) return root;
if (root->val < p->val) return lowestCommonAncestor(root->right, p, q);
if (root->val > p->val) return lowestCommonAncestor(root->left, p, q);
return NULL;
}
};
因为p、q节点顺序未知,所以需要在判断前使用swap函数进行规范。
701. 二叉搜索树中的插入操作
需要明确的是,不需要调整二叉树的结构,直接在叶子节点进行添加即可。
①判断当前节点的孩子节点
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
TreeNode* insertIntoBST(TreeNode* root, int val) {
if (root == NULL) {
TreeNode* node = new TreeNode(val);
return node;
}
else
return traversal(root, val);
}
TreeNode* traversal(TreeNode* root, int val) {
if (root == NULL) return NULL;
if (root->val > val) {
if (traversal(root->left, val) == NULL) {
TreeNode* node = new TreeNode(val);
root->left = node;
return root;
}
}
else {
if (traversal(root->right, val) == NULL) {
TreeNode* node = new TreeNode(val);
root->right = node;
return root;
}
}
return root;
}
};
②直接判断当前节点
直接判断当前节点,只要节点为空,即找到插入新节点的位置。
为了保证第一次终止的空节点为目标位置,需要利用二叉搜索树的性质,来寻找合适的搜索路径。又因为题目说明所有值 Node.val 是 独一无二的保证 val 在原始BST中不存在,所以不需要考虑节点相等的情况,代码如下:
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
TreeNode* insertIntoBST(TreeNode* root, int val) {
if (root == NULL) {
TreeNode* node = new TreeNode(val);
return node;
}
if (root->val > val)root->left = insertIntoBST(root->left, val);
else root->right = insertIntoBST(root->right, val);
return root;
}
};
450. 删除二叉搜索树中的节点
需要分情况进行讨论:
有以下五种情况:
-
第一种情况:没找到删除的节点,遍历到空节点直接返回了
-
找到删除的节点
-
第二种情况:左右孩子都为空(叶子节点),直接删除节点, 返回NULL为根节点
-
第三种情况:删除节点的左孩子为空,右孩子不为空,删除节点,右孩子补位,返回右孩子为根节点
-
第四种情况:删除节点的右孩子为空,左孩子不为空,删除节点,左孩子补位,返回左孩子为根节点
-
第五种情况:左右孩子节点都不为空,则将删除节点的左子树头结点(左孩子)放到删除节点的右子树的最左面节点的左孩子上,返回删除节点右孩子为新的根节点。
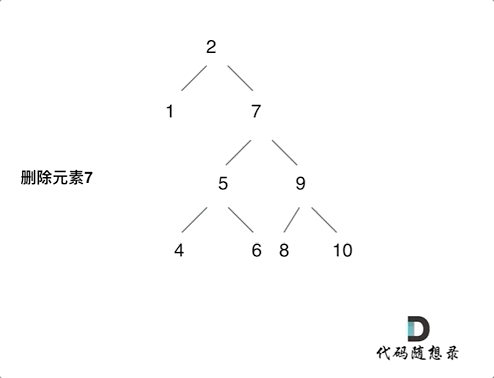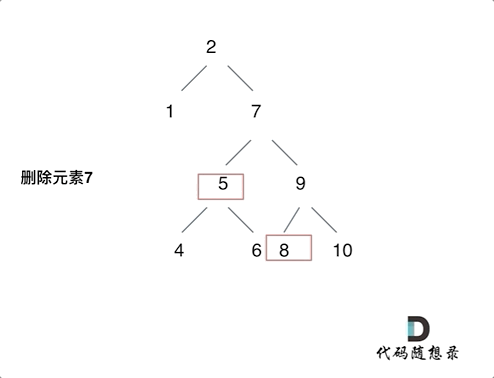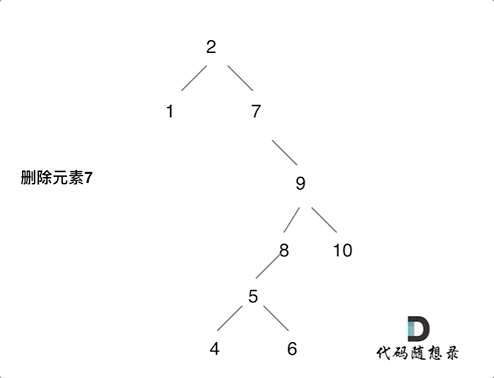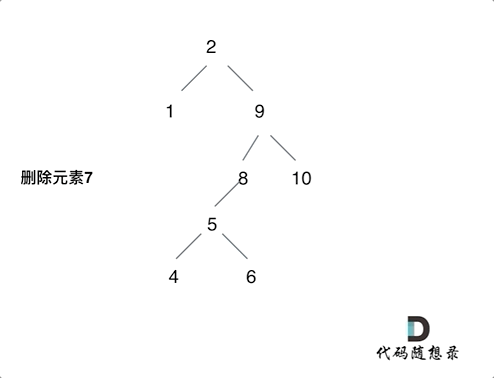
-
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
TreeNode* deleteNode(TreeNode* root, int key) {
if (root == NULL) return NULL;
if (root->val == key) {
// 分情况讨论
if (root->left == NULL && root->right == NULL) {
delete root;
return NULL;
}
else if (root->left != NULL && root->right == NULL) {
TreeNode* tmp = root->left;
delete root;
return tmp;
}
else if (root->left == NULL && root->right != NULL) {
TreeNode* tmp = root->right;
delete root;
return tmp;
}
else {
TreeNode* cur = root->right;
while (cur->left != NULL) cur = cur->left;
cur->left = root->left;
TreeNode* right = root->right;
delete root;
return right;
}
}
root->left = deleteNode(root->left, key);
root->right = deleteNode(root->right, key);
return root;
}
};
根据二叉搜索树的特性,在遍历路径的时候可以剪枝一下,注意这里也需要整棵树遍历:
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
TreeNode* deleteNode(TreeNode* root, int key) {
if (root == NULL) return NULL;
if (root->val == key) {
// 分情况讨论
if (root->left == NULL && root->right == NULL) {
delete root;
return NULL;
}
else if (root->left != NULL && root->right == NULL) {
TreeNode* tmp = root->left;
delete root;
return tmp;
}
else if (root->left == NULL && root->right != NULL) {
TreeNode* tmp = root->right;
delete root;
return tmp;
}
else {
TreeNode* cur = root->right;
while (cur->left != NULL) cur = cur->left;
cur->left = root->left;
TreeNode* right = root->right;
delete root;
return right;
}
}
if (root->val > key) root->left = deleteNode(root->left, key);
else root->right = deleteNode(root->right, key);
return root;
}
};