代码随想录算法训练营Day21|530. 二叉搜索树的最小绝对差、501. 二叉搜索树中的众数、236. 二叉树的最近公共祖先
530. 二叉搜索树的最小绝对差
利用二叉搜索树递增且有序的性质,将问题转化为在一个有序数组上求两个数最小差值的问题。
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
int getMinimumDifference(TreeNode* root) {
vector<int> vec;
if (root != NULL) traversal(root, vec);
int min_diff = INT_MAX;
for (int i = 0; i < vec.size() - 1; i++) {
min_diff = abs(vec[i] - vec[i + 1]) < min_diff ? abs(vec[i] - vec[i + 1]) : min_diff;
}
return min_diff;
}
void traversal(TreeNode* node, vector<int>& vec) {
if (node == NULL) return;
traversal(node->left, vec);
vec.push_back(node->val);
traversal(node->right, vec);
return;
}
};
注意代码中我们还使用了abs函数保证差值非负,但由于BST的中序遍历为递增数列,所以后值与前值相减必为非负数,这个操作是非必要的:
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
int getMinimumDifference(TreeNode* root) {
vector<int> vec;
if (root != NULL) traversal(root, vec);
int min_diff = INT_MAX;
for (int i = 0; i < vec.size() - 1; i++) {
min_diff = min(vec[i + 1] - vec[i], min_diff);
}
return min_diff;
}
void traversal(TreeNode* node, vector<int>& vec) {
if (node == NULL) return;
traversal(node->left, vec);
vec.push_back(node->val);
traversal(node->right, vec);
return;
}
};
501. 二叉搜索树中的众数
整体思路是遍历整棵树,用map统计频率,把频率排序吼再取前面高频的元素的集合。
这里的重点在于统计频率,我们记录节点值的同时也需要统计节点值出现的次数。由于后期需要进行排序,这里我们使用无序的unordered_map进行计数即可:
unordered_map<int, int> map;
因为无法直接对map中的value排序(C++中如果使用std::map或者std::multimap只可以对key排序,但不能对value排序)。所以要把map转化数组vector,再进行排序,当然vector里面放的是pair<int, int>类型的数据,使用map给vector赋值时需要注意。
vector<pair<int, int>> vec(map.begin(), map.end());
sort(vec.begin(), vec.end(), cmp); // 给频率排个序
另外由于我们不是根据key进行排序,这里需要自定义比较函数,来确定排序后的升/降序和选择哪个键进行比较。
bool static cmp (const pair<int, int>& a, const pair<int, int>& b) {
return a.second > b.second; // 按照频率从大到小排序
}

完整代码如下:
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
vector<int> findMode(TreeNode* root) {
unordered_map<int, int> map;
vector<int> res;
if (root != NULL) traversal(root, map);
// 给指定的容器适配对应的比较函数
vector<pair<int, int>> vec(map.begin(), map.end());
sort(vec.begin(), vec.end(), cmp);
for (int i = 0; i < vec.size(); i++) {
if (vec[i].second == vec[0].second)
res.push_back(vec[i].first);
}
return res;
}
bool static cmp(pair<int, int> a, pair<int, int> b) {
return (a.second > b.second);
}
void traversal(TreeNode* node, unordered_map<int, int>& map) {
if (node == NULL) return;
traversal(node->left, map);
map[node->val]++;
traversal(node->right, map);
return;
}
};
236. 二叉树的最近公共祖先
一开始思路是:如果找到一个节点,发现左子树出现结点p,右子树出现节点q,或者 左子树出现结点q,右子树出现节点p,那么该节点就是节点p和q的最近公共祖先。
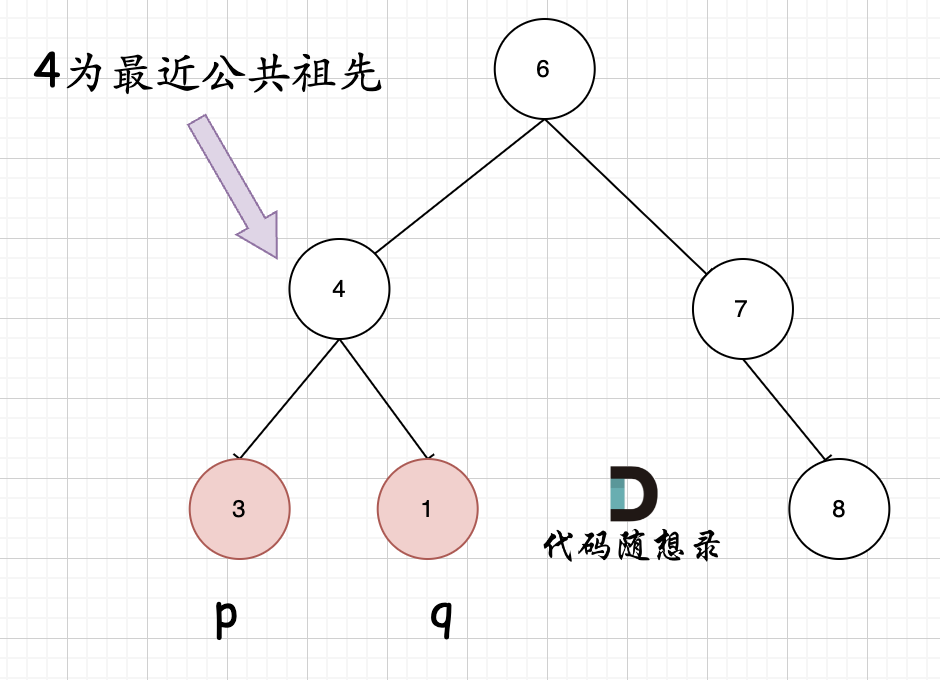
所以考虑用容器vector后序遍历二叉树,当容器同时包含两个节点时,返回当前节点即可。代码如下:
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode(int x) : val(x), left(NULL), right(NULL) {}
* };
*/
class Solution {
public:
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
unordered_set<int> set;
p_value = p->val;
q_value = q->val;
return traversal(root, set);
}
TreeNode* traversal(TreeNode* node, unordered_set<int>& set) {
if (node == NULL) return NULL;
// 遵循后序遍历顺序
traversal(node->left, set);
traversal(node->right, set);
unordered_set<int>::iterator iterQ = set.find(q_value);
unordered_set<int>::iterator iterP = set.find(p_value);
if (iterQ != set.end() && iterP != set.end()) return node;
else set.insert(node->val);
return NULL;
}
private:
int p_value;
int q_value;
};
但这种方法忽略了节点本身p(q),它拥有一个子孙节点q(p)。的情况:
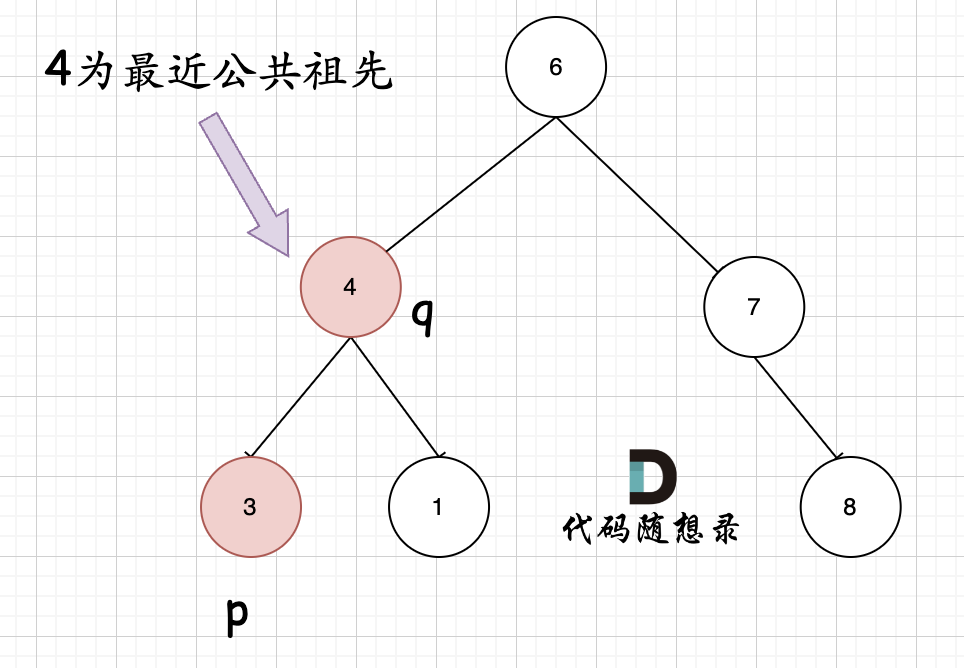
同时考虑两种情况的话,边界的判断就会出现不统一的现象。
正确思路是:如果 root == q,或者 root == p,说明找到 q p ,则将其返回,这个返回值,后面在中节点的处理过程中会用到:
- 如果left 和 right都不为空,说明此时root就是最近公共节点。这个比较好理解
- 如果left为空,right不为空,就返回right,说明目标节点是通过right返回的,反之依然。
这种思路的前提在于不立即返回,而是遍历整棵树后再对左右子树进行判断:左右孩子节点不为空的情况好进行判断,主要是目标节点同时是根节点的情况:
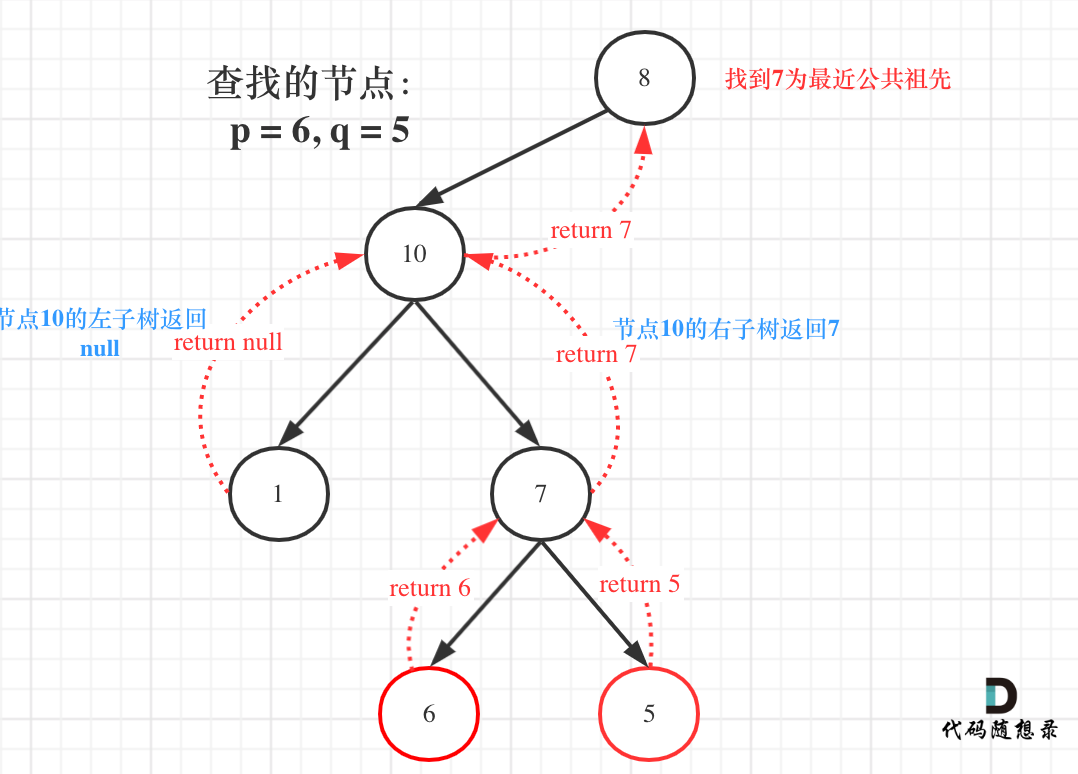
如此一来对于节点「10」,其返回右孩子节点便会往下遍历找到目标的根节点,如果根节点本身就是目标节点,那他不会考虑左右孩子节点而是直接返回。代码如下:
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode(int x) : val(x), left(NULL), right(NULL) {}
* };
*/
class Solution {
public:
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
if (root == NULL) return NULL;
// 如果找到目标节点,直接返回(非空即可)
if (root == p || root == q) return root;
TreeNode* left = lowestCommonAncestor(root->left, p, q);
TreeNode* right = lowestCommonAncestor(root->right, p, q);
if (left != NULL && right != NULL) return root;
// 并存在答案,所以分情况讨论
if (left == NULL && right != NULL) return right;
else if (left != NULL && right == NULL) return left;
else return NULL;
}
};