可持久化线段树——主席树
引入(P3834 【模板】可持久化线段树 2 - 洛谷)
看看题面:
题目描述
如题,给定 \(n\) 个整数构成的序列 \(a\),将对于指定的闭区间 \([l, r]\) 查询其区间内的第 \(k\) 小值。
数据规模与约定
- 对于 \(100\%\) 的数据,满足 \(1 \leq n,m \leq 2\times 10^5\),\(|a_i| \leq 10^9\),\(1 \leq l \leq r \leq n\),\(1 \leq k \leq r - l + 1\)。
看着像线段树,可怎么做呢?
对于一个普通的线段树,如果要维护它的历史版本(即每一次修改后版本都要存下来),这种情况下是要开 \(M\)(操作次数)个线段树吗?
不可能的(不然我不会在这里说) 。
因为在每次修改时,只会影响到修改节点所在的一条链(单点修改),即 \(\log n\) 个节点,那么……
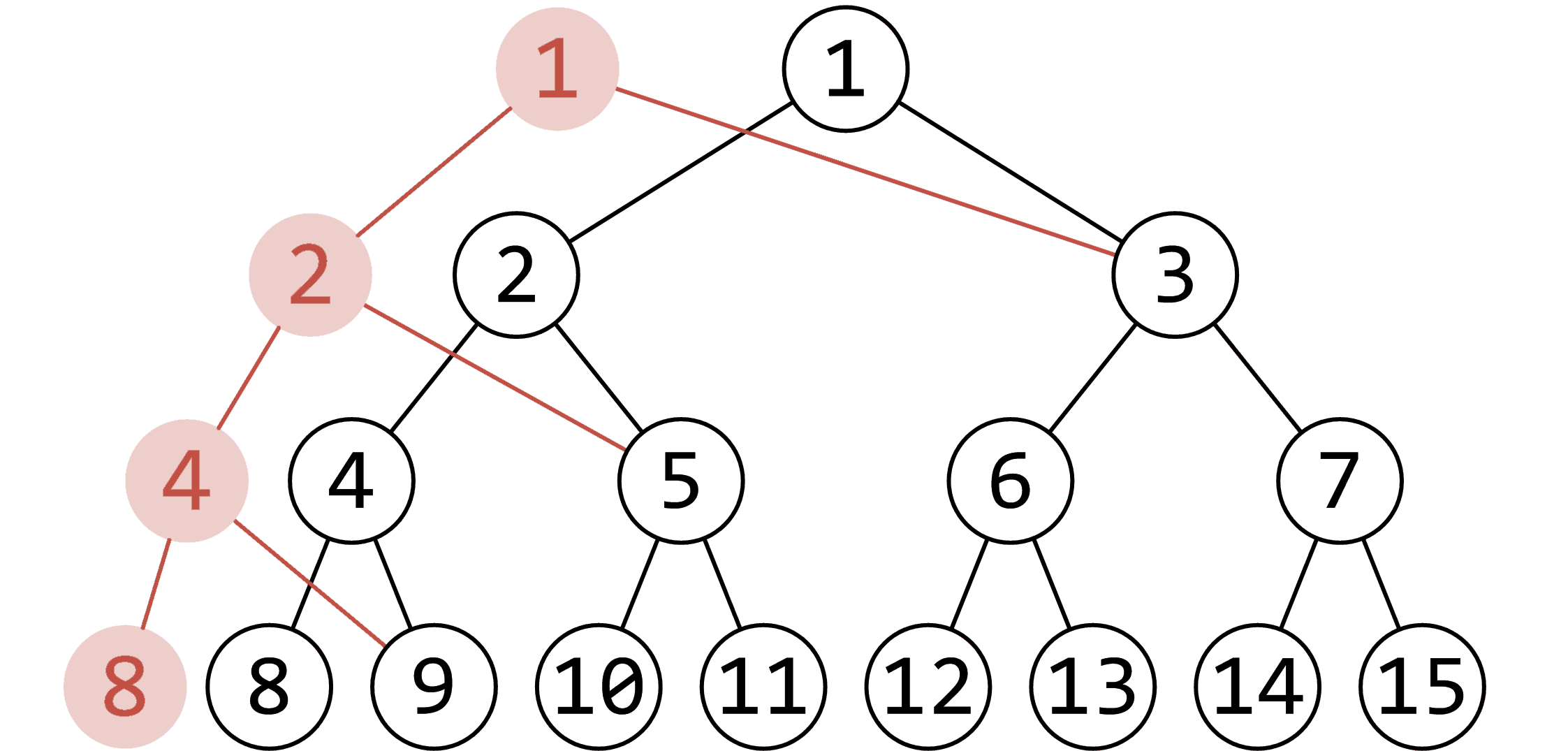
我们就可以在每次修改时将改变的节点给“提”出来,如上图。
这就是主席树。
这样空间复杂度就只有 \(\mathcal{O}((N + M)\log N)\) 了。
而此题就是经典的区间静态第 \(k\) 小问题。
- 这就需要维护值域了,即主席树的每个节点维护的不是位置,而是一个范围,而节点的值为这个范围中的数的个数。
- 而此题 \(|a_i| \leq 10^9\) ,很明显需要离散化。
- 并且主席树也不能用节点编号 \(\times \ 2\) 和 \(\times \ 2 + 1\) 来表示了,那么节点中的 \(l\) 和 \(r\) 就用来表示左右子节点的编号。
- 还要单独开一个 \(root\) 数组来存 \(m\) 个根节点。
那么接下来就看看此题的细节吧!
分段讲解
-
节点需定义的信息
struct Node{
int l, r, cnt;
// l, r 为左右子节点编号,cnt 即为此范围中数的个数
// 范围其实是不用存的,二分时就可以算出来
}tr[N << 5]; // 计算得出,一定要尽量开大点
-
离散化
用 \(vector\) 来离散化。
定义一个 \(\rm{find}\) 函数来查找数值在离散化数组中的位置。
vector<int> nums;
// 此处省略...
inline int find(int x){
return lower_bound(nums.begin(), nums.end(), x) - nums.begin();
// 一个 lower_bound 即可解决
}
// 省略...
int main(){
for(int i = 1; i <= n; ++i){
scanf("%d", &a[i]);
nums.push_back(a[i]);
}
sort(nums.begin(), nums.end());
nums.erase(unique(nums.begin(), nums.end()), nums.end());
// 离散化基本过程,排序,删除重复元素
}
-
\(\rm{build}\)
int build(int l, int r){
int u = ++idx;
// 节点编号也直接像建图一样依次加
if(l == r) return u;
// 这里是有返回值的,为了在后面子节点能直接上传节点编号
int mid = l + r >> 1;
tr[u].l = build(l, mid);
tr[u].r = build(mid + 1, r);
return u;
}
-
\(\rm{insert}\)
用来在主席树中插入一个新的值。
int insert(int p, int l, int r, int x){
/*
p表示原来的根节点(就是需要“提”出来的那个节点)
l, r是节点的左右边界,即维护的值域
x是插入的值
*/
int q = ++idx;
// 新建一个节点,“提”出来
tr[q] = tr[p];
// 首先复制原节点的信息
if(l == r){
++tr[q].cnt;
// 到子节点时,x就是个确定的值了,直接cnt++
return q;
// 记得返回编号
}
int mid = l + r >> 1;
if(x <= mid) tr[q].l = insert(tr[p].l, l, mid, x);
// x在左半边,到左子节点修改,原来的根节点也往下找左子节点,最后记得顺便记录左子节点编号
else tr[q].r = insert(tr[p].r, mid + 1, r, x);
// x在右半边,同上
tr[q].cnt = tr[tr[q].l].cnt + tr[tr[q].r].cnt;
// 更新cnt ,相当于普通的线段树中的pushup
return q;
}
-
\(\rm{query}\)
要找到 \([l,r]\) 中的第 \(k\) 小值,就可以在查询的时候同时找到以 \(root_{l - 1}\) 和 \(root_r\) 为根节点的子树(即插入了前 \(l - 1\) 个数的区间\([1, l - 1]\) 和插入了前 \(r\) 个数的区间 \([1, r]\) 的历史版本),同时向下搜两个子树的节点,那么 \([l,r]\) 中每个节点 (区间) 中的 \(cnt\) 就可以直接用 \([1,r]\) 中的节点的 \(cnt\) 减去 \([1, l - 1]\) 中节点的 \(cnt\) 。
int query(int q, int p, int l, int r, int k){
/*
q是[1, r]中的节点,p是[1, l - 1]中的节点
l, r还是节点维护的值域
k是要找以此节点为根节点的子树中的第k小值
*/
if(l == r) return l; // 到叶节点直接返回值
int cnt = tr[tr[q].l].cnt - tr[tr[p].l].cnt;
// 上面讲的,[l, r]的cnt = [1, r]的cnt - [1, l - 1]的cnt ,这里直接看左半边的,后面方便比较
// 此处说的 l, r 是查询 [l, r]的第k小值 中的,不要和结点维护的值域搞混了
int mid = l + r >> 1;
if(k <= cnt) return query(tr[q].l, tr[p].l, l, mid, k);
// 因为左半边的每个数都比右半边的小,所以如果要查找的排名比左半边的总个数小,那么第k小的数肯定在左半边
else return query(tr[q].r, tr[p].r, mid + 1, r, k - cnt);
// 否则同上,到右子节点去找
}
最后,完整 \(\text{Code}\)
#include <iostream>
#include <cstring>
#include <cstdio>
#include <algorithm>
#include <vector>
using namespace std;
const int N = 100010;
int n, m;
int a[N];
int root[N], idx;
vector<int> nums;
struct Node{
int l, r, cnt;
}tr[21 * N];
inline int find(int x){
return lower_bound(nums.begin(), nums.end(), x) - nums.begin();
}
int build(int l, int r){
int u = ++idx;
if(l == r) return u;
int mid = l + r >> 1;
tr[u].l = build(l, mid);
tr[u].r = build(mid + 1, r);
return u;
}
int insert(int p, int l, int r, int x){
int q = ++idx;
tr[q] = tr[p];
if(l == r){
++tr[q].cnt;
return q;
}
int mid = l + r >> 1;
if(x <= mid) tr[q].l = insert(tr[p].l, l, mid, x);
else tr[q].r = insert(tr[p].r, mid + 1, r, x);
tr[q].cnt = tr[tr[q].l].cnt + tr[tr[q].r].cnt;
return q;
}
int query(int q, int p, int l, int r, int k){
if(l == r) return r;
int cnt = tr[tr[q].l].cnt - tr[tr[p].l].cnt;
int mid = l + r >> 1;
if(k <= cnt) return query(tr[q].l, tr[p].l, l, mid, k);
else return query(tr[q].r, tr[p].r, mid + 1, r, k - cnt);
}
int main(){
scanf("%d%d", &n, &m);
for(int i = 1; i <= n; ++i){
scanf("%d", &a[i]);
nums.push_back(a[i]);
}
sort(nums.begin(), nums.end());
nums.erase(unique(nums.begin(), nums.end()), nums.end());
root[0] = build(0, nums.size() - 1);
// root[0]先赋值为 build 返回的根节点编号
for(int i = 1; i <= n; ++i)
root[i] = insert(root[i - 1], 0, nums.size() - 1, find(a[i]));
// 插入n个数,上一个根节点为 root[i - 1],左右边界如上,注意插入的值要变成 find(a[i])
int l, r, k;
while(m--){
scanf("%d%d%d", &l, &r, &k);
printf("%d\n", nums[query(root[r], root[l - 1], 0, nums.size() - 1, k)]);
// 注意query返回的是离散数组中的位置,同时搜索以 root[r] 和 root[l - 1] 为根节点的子树
}
return 0;
}
\(\text{Updeted on 2022.12.22}\)