今天看到一道题:
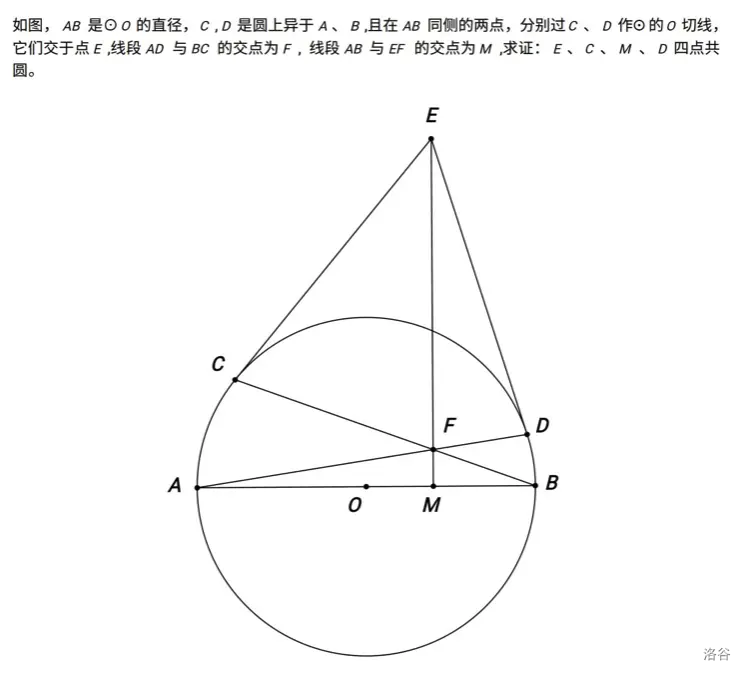
可能有强神一眼秒了.初见此题时,没什么思路.而后发现有 \(O\)、\(C\)、\(E\)、\(D\) 四点共圆且 \(OE\) 为直径,于是想到证 \(EM \perp AB\).然而在如何证这里卡了挺久,后来才终于想到解法.
证明:
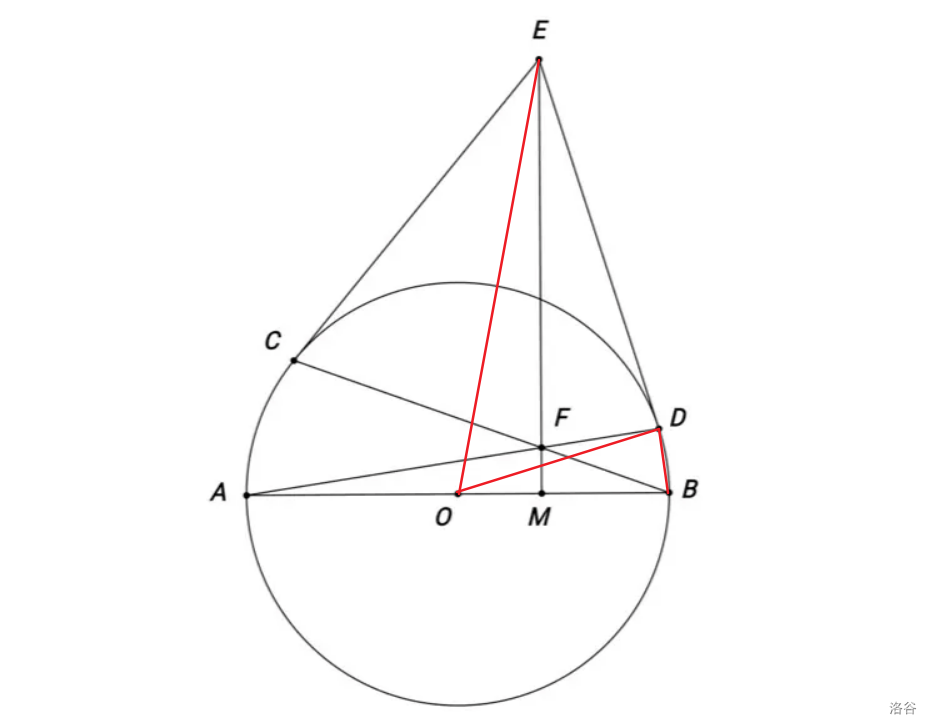
如图,连结 \(DO\)、\(DB\)、\(EO\).由 \(OC \perp CE\),\(OD \perp DE\),易知 \(C\)、\(D\) 在以 \(OE\) 为直径的圆上,且 \(\angle EDO = 90^\circ\).由 \(AB\) 是直径,知 \(\angle FDB = 90^\circ = \angle EDO\).又有 $\displaystyle\angle OED = \frac{\angle OED}{2} = \frac{180^\circ - \angle COD}{2} = \frac{\angle COA + \angle DOB}{2} = \angle CBA + \angle DAB = \angle DFB $,于是 \(Rt\triangle EOD \sim Rt\triangle FBD\),即有 \(\displaystyle\frac{ED}{FD} = \frac{OD}{BD} = \frac{OB}{BD}\).又根据弦切角定理,有 \(\angle EDF = \angle DBO\),即知 \(\triangle EDF = \triangle OBD\).于是,由 \(OD = OB\) 知 \(ED = EF\),即有 \(\angle EFD = \angle EDF = \angle DBO\).又由 \(\angle EFD + \angle DFM = 180^\circ\) 知 \(\angle DBM + \angle DFM = 180^\circ\),于是 \(F\)、\(D\)、\(B\)、\(M\) 四点共圆,则 \(\angle EMB = 180^\circ - \angle FDB = 90^\circ\),所以 \(\angle EMO = 90^\circ\),即 \(M\) 在 \(OE\) 为直径的圆上,所以 \(E\)、\(C\)、\(M\)、\(D\) 四点共圆.证毕.
所以,在想几何题时一定要注意一些角和边之间的关系,可以先猜想再尝试证明,从结论往前推一些,从而得解.
标签:triangle,circ,一道,180,几何,frac,angle,90 From: https://www.cnblogs.com/wf715/p/A-Geometry-Problem.html